聚合物纳米复合体系中聚合物结构及动力学研究进展
2020-05-19戴利均孙昭艳
戴利均,孙昭艳
(1.中国科学院长春应用化学研究所,高分子物理与化学国家重点实验室,长春 130022;2.中国科学院大学,北京 100039)
聚合物纳米复合材料是一类由粒径为1~100 nm的纳米颗粒和具有不同拓扑性质的聚合物基质构成的创新型功能材料,是目前材料领域和软物质科学研究的关注热点之一.与传统聚合物材料和复合材料相比,聚合物纳米复合材料由于兼具纳米粒子和聚合物的性质而展现出特有的力学[1~5]、 光学[6,7]、 电磁学[8~10]和阻燃[11,12]等特性,在材料应用方面具有更广阔的应用前景.环氧树脂是一种应用广泛的热固性聚合物,虽然具有较高的强度和刚性度,但韧性不足,而添加各种纳米填料能显著改善环氧树脂的韧性[13].硅虽然具有储量多、 成本低及比容量高等优势,但硅在充放电过程中会造成体积膨胀,而在硅纳米颗粒上覆盖一层自愈性聚合物,能有效地抑制硅体积膨胀,从而提高锂电池充放电循环寿命[14].
研究表明,聚合物纳米复合材料具有巨大的可调控性,其性质不仅依赖于材料自身的制备、 表征及加工[15~17],也依赖于聚合物和纳米粒子的特性及形态[8,18,19],与纳米粒子形状、 尺寸、 取向、 长径比、 体积分数及聚合物链结构、 链刚性、 相对分子质量等因素密切相关[20~27].多因素的存在也使得人们难以精确控制并获得具有理想性质的聚合物纳米复合物.大量综述类的文章系统性地总结了纳米粒子分散行为[28]、 聚合物链和纳米粒子动力学[29~32]、 聚合物纳米复合物加工和应用[33,34]、 聚合物纳米复合物计算模拟和理论方法分析[35~37]等的研究进展.微观尺度上聚合物链结构和动力学性质的变化是影响聚合物纳米复合材料性能的重要因素之一.本文以现有的计算模拟结果和实验结果及本课题组的部分研究成果为基础,从聚合物链结构和动力学因素出发,系统地阐述了目前含球状纳米粒子聚合物复合体系中的聚合物链结构及动态性质的相关研究进展.
1 聚合物结构
1.1 聚合物尺寸
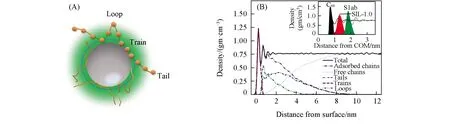
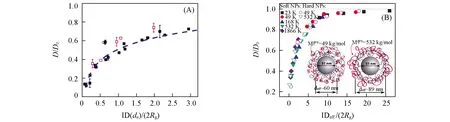
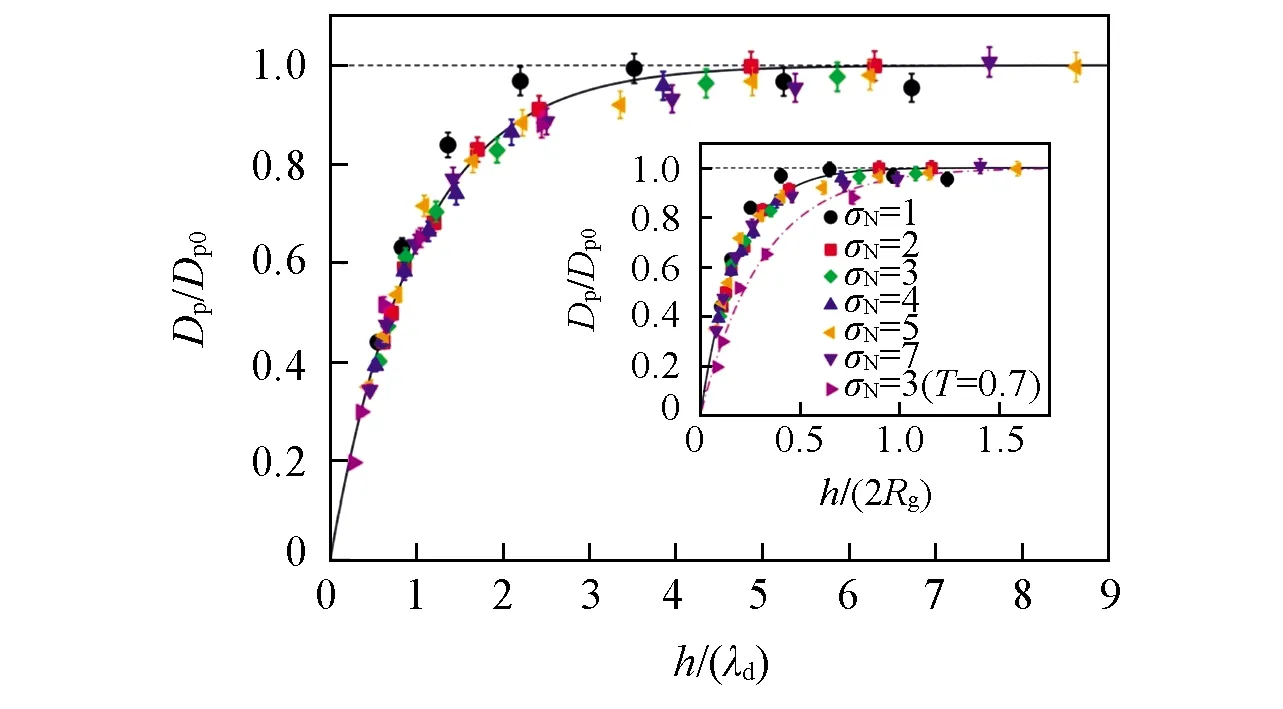
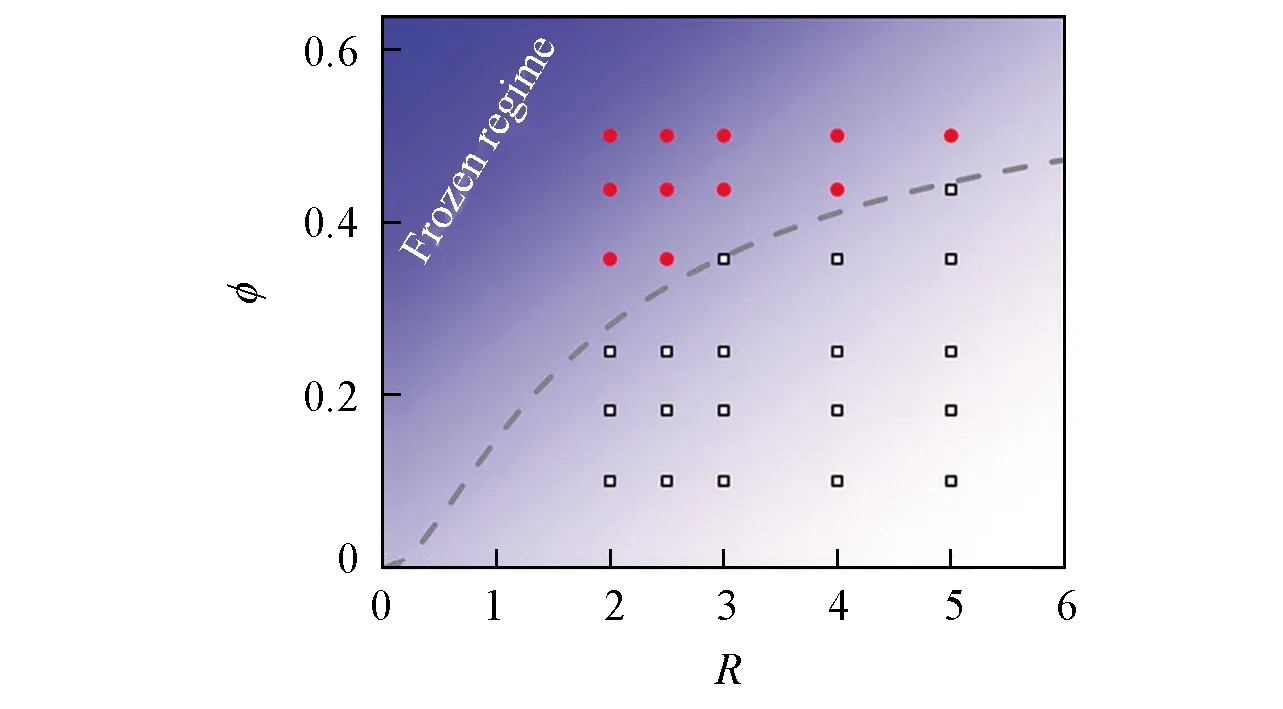
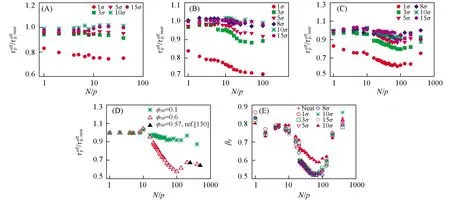
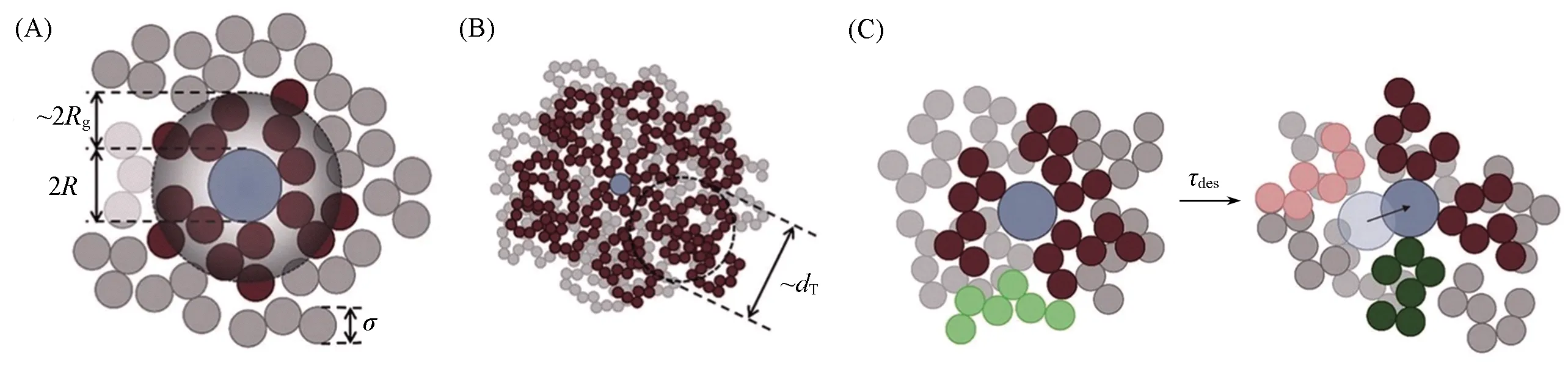
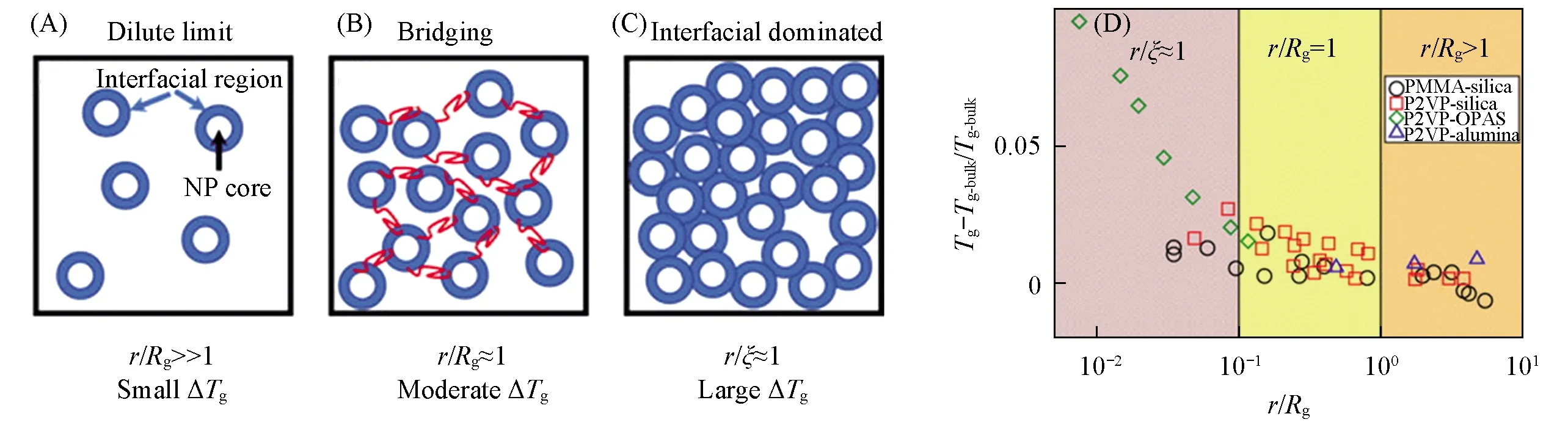
在一定程度上,聚合物结构和构象的变化会影响材料的流变性质、 力学性质和摩擦性质.在聚合物纳米复合物中,加入的纳米粒子会扰动聚合物结构.实验发现,在纳米粒子的作用下聚合物链会发生收缩和“溶胀”行为[38~40],并且链尺寸的增大与纳米粒子的强吸引作用、 聚合物尺寸(Rg)是否大于纳米粒子尺寸(Rnp)及纳米粒子分散性等几个条件密切相关[41].早期的聚合物纳米复合物研究发现[38],当Rg 事实上,实验中很难精确控制复合体系中纳米粒子的分散性,也很难制备纳米粒子完全单分散的聚合物,这就可能会导致最终结果的不准确,而计算模拟能很好地避免这些问题.计算模拟不仅能直观地描述聚合物纳米复合物的微观性质,而且能够指导实验及补充实验,并且获得目前实验难以观察或控制的信息,从而更加深入地了解聚合物纳米复合物的结构及动力学的内在本质.在计算模拟中,纳米粒子的加入引起的聚合物尺寸增大、 不变或减小的主要机理仍然不是很清晰[48~50].早期研究主要集中于低纳米粒子含量的聚合物体系,聚合物链“感受不到”任何纳米粒子的作用,对应尺寸变化主要与纳米粒子加入引起的排除体积效应有关.多级模拟方法(粗粒化Monte Carlo和联合原子模型)研究发现,在二氧化硅体积分数极低的体系中,聚合物尺寸(Rg)与自身相对分子质量的0.5次方[(Mn)0.5]呈线性关系,纳米粒子对聚合物尺寸影响特别微弱[51].随着计算手段的发展,人们进一步分析了更高纳米粒子含量下聚合物尺寸的变化信息[41].在纳米粒子含量较高的体系中,聚合物不仅能“感受”到其它纳米粒子的存在,而且部分链节会接触纳米粒子表面,形成桥连效应,从而大幅度影响聚合物尺寸.与含较低浓度纳米粒子的体系相比,含高浓度纳米粒子的体系中聚合物链尺寸被纳米粒子过度拉伸[52],纳米粒子尺寸越小对聚合物尺寸的影响越大,定性地与实验结果相吻合[39].在排斥纳米粒子的作用下,聚合物尺寸几乎与纳米粒子含量无关,这与实验中测得的数据一致[40].以上模拟结果表明,聚合物纳米复合物体系中聚合物尺寸变化不仅依赖于纳米粒子尺寸及纳米粒子和聚合物之间的作用势,而且也依赖于纳米粒子之间的平均间距. 纳米粒子的加入会引起聚合物基质的构象熵损失,使得部分聚合物吸附在纳米粒子的表面,造成纳米粒子附近的聚合物性质不同于本体相的聚合物性质.在一定纳米粒子含量下,纳米粒子附近由聚合物链形成的界面层对聚合物纳米复合材料性质起着决定性的作用.界面层结构主要分为界面构象和界面厚度两部分. 在聚合物纳米复合体系中,聚合物根据链节是否和纳米粒子接触分为吸附链和自由链.由图1(A)可见,吸附链的构象主要由loop,train和tail三部分组成[53].其中,Train指处于纳米粒子表面的吸附链节; loop指连接两个train的连续链节集,且连续链节集偏离于纳米粒子表面; tail指一个train末端到一个链末端的链节集.目前,大量理论和模拟研究主要集中于探索平面界面处的吸附链节构象变化[54~59].早在三十几年前,研究人员采用数值理论,即平均场格点模型(Scheutjens-Fleer格点模型),预测了这3种构象的分布行为[53],比较了由Hoeve理论预测在无作用势情况下的吸附链train和loop构象分布结果[60].Matsuda等[61]采用全原子分子动力学技术证实了Scheutjens-Fleer格点理论的预测.近年来,Vilgis等[62]采用粗粒化模拟方法发现,柔性聚合物链构象分布与理论预测相似.增加聚合物链刚性虽然会造成聚合物构象熵损失,但loop和tail尺寸分布变化仍然近似于柔性链体系中的理论预测关系[63].Vilgis等[57,64]建立了在平坦无结构化平面环境中拉力诱导的单条线形链不同构象平均尺度的理论表达式,预测了拉力诱导下该链的吸附-解吸附相图,并使用Monte Carlo模拟证实了上述理论表达式.此外,结合Monte Carlo方法和分子动力学模拟技术,Daoulas等[65]发现,石墨表面处吸附的聚乙烯层结构与聚乙烯链长的依赖关系强于Scheutjens-Fleer格点模型预测的关系.薄膜和聚合物纳米复合物之间具有一定的类似性.与薄膜体系相比,纳米粒子附近的聚合物链拥有更高的自由度,意味着链运动更快.纳米粒子尺寸越小,对应的比表面积越大,对聚合物链作用更大,可吸附更多的链节,从而阻碍聚合物链节运动,并影响纳米粒子附近聚合物构象行为.从图1(B)可见,纳米粒子尺寸越小,会使得纳米粒子附近的聚合物链所需要的自由能代价越大,进而导致train链节数目增加,对应的train链尺寸分布变窄[66].Tail密度分布区域一直大于loop密度分布区域,不依赖于纳米粒子尺寸大小. Fig.1 Schematic representation of adsorbed chains on the surface of nanoparticle(A) and density distribution for PE500-Slab as a function of distance from the surface and decomposition following Scheutjens-Fleer(B)[53] (B) Copyright 1980,American Chemical physics.Inset of (B) provides profiles for selected systems[66].Copyright 2012,American Institute of Physics. Fig.2 lint vs. C∞ at temperatures close to Tg(T=1.05Tg) from different techniques(A) and at T=1.2Tg in PNCs(B) Blue squares present literature data.The error bars for the blue squares include the measurements from different groups and different methods.The dashed-black line presents recent MD simulations assuming the bead size σ=0.4 nm[80].Copyright 2017,American Chemical Society. 界面构象决定着界面厚度大小.大部分研究结果表明,界面厚度处于1~6 nm之间[67~70],界面厚度和聚合物自身的尺寸有关[23,71~74].界面厚度大小依赖于纳米粒子尺寸、 纳米粒子和聚合物作用势、 链长等因素.增加纳米粒子和聚合物链之间的作用势虽然会引起界面层密度的增加,但不影响界面厚度[22,23,75].此外,链增长可能会促使界面层增厚.Kim等[76]发现,在高温下增加聚乙二醇链长会增大二氧化硅界面层厚度.但近年来的研究结果表明,增加聚合物相对分子质量反而会降低纳米粒子界面厚度[77].小角X射线散射和样本密度测量的结构揭示,聚合物相对分子质量的增加会引起界面层链节密度的降低.Cheng等[77]认为界面厚度变化和吸附聚合物链的堆积性相关,即链越长,界面层中loop和tail构象尺寸越长.长链需要跨越很大的熵位垒才能发生构象变化,而且loop-loop之间的排斥影响纳米粒子界面处的链节堆积过程,最终使链堆积变得松散.当纳米粒子尺寸近似于或小于链尺寸时,改变纳米粒子尺寸会严重影响界面层性质[78].Colby等[79]采用宽频介电谱(BDS)测得,二氧化硅纳米粒子尺寸的增加会引起界面层增厚,而且纳米粒子尺寸趋向于无穷大时,界面厚度趋近于聚合物尺寸.全原子Monte Carlo模拟也得到了纳米粒子尺寸和界面层厚度之间的类似关系,即纳米粒子尺寸增加造成纳米粒子界面厚度增加[66].增加链刚性会导致聚合物构象熵损失,造成聚合物动力学松弛变慢.Sokolov等[80]采用不同仪器测得不同链刚性体系中界面厚度的大小,并且引入了文献[81]的界面层厚度数据.由图2(A)可见,这3种仪器测得的数据虽然没有直接表明界面厚度和Rg的关系,但当体系温度接近于玻璃化转变温度(Tg)时链刚性增加会引起界面层增厚.此外,Sokolov等[80]也强调了T=1.2Tg时界面厚度和链刚性的关系,并且结合了其它文献测得的在高温(T=1.2-1.3Tg)下界面层厚度数据[69,76,77,79,81~93].由图2(B)可见,界面厚度和链刚性之间存在一个临界链刚性值,当超过该临界点(C∞,不同化学结构聚合物体系或不同方法得到的临界点不同,图中的临界点大概处于5~7),界面厚度随着链刚性单调增加.而界面厚度和链刚性的关系已经得到了粗粒化分子动力学模拟的证实[63].由图2可以发现,降低温度会造成界面厚度增加,类似的界面厚度和温度之间的关系同样出现在不同体系中.Kumar等[94]使用小角中子散射仪研究了二氧化硅纳米粒子表面处聚(2-乙烯基吡啶)(P2VP)在受限层停留时间的持久性,发现界面厚度和温度相对较强的关系主要依赖于二氧化硅纳米粒子表面处单条聚合物链的吸附链节数目.他们认为单个吸附链节发生解吸附所需的活化能较少,因此很容易在更广泛的温度范围内发生解吸附行为.更多吸附链节发生解吸附需要更多的活化能量,导致链节发生吸附-解吸附行为的温度范围变窄.基于薄膜体系的理论和模拟研究发现界面厚度和动态异质性长度存在一定关系[95,96].由于聚合物纳米复合物和薄膜的相似性[97,98],在聚合物纳米复合体系中的界面厚度可能也与动态异质性长度有关,这对于理解界面层聚合物结构和动力学关系非常重要. 早期的理论研究[99~101]指出,聚合物在通过各向异性障碍物时,由于自身构象熵损失导致其扩散系数减小.在聚合物纳米复合体系中,相邻纳米粒子表面之间平均空间间距(ID)能够半定量地预测聚合物的扩散系数的变化规律[102].假设硬球粒子能均一分散到体系中,对应硬球之间的ID可定义为[103] (1) 式中:φmax为硬球最大堆积分数,实际值依赖于具体的堆积方式,简单立方堆积对应于0.523,体心立方堆积对应于0.680,面心立方堆积对应于0.740,随机紧密堆积对应于0.637.在聚合物纳米复合体系中,假定纳米粒子为硬球粒子,根据式(1)可知: 一定纳米粒子体积分数下,纳米粒子尺寸越小,对应的纳米粒子表面间距越小,对聚合物扩散系数影响更严重[100,101]. 弹性反冲仪(ERD)测试[102,104]发现,中性(Neutral)纳米粒子的存在能够阻碍聚合物运动,减慢聚合物扩散,且对应尺寸越小对聚合物扩散的影响越大.实验结果表明[102],聚合物的扩散系数与纳米粒子平均间距和高分子链尺寸之比[受限参数ID/(2Rg)]有关,且可以归于同一主曲线,即ID/2Rg能合理地描述聚苯乙烯在含中性纳米粒子复合体系中的扩散行为(图3)[104,105].增加纳米粒子和聚合物之间的作用势能够增加对应的吸引焓,提高纳米粒子在聚合物基质中的分散性,同时影响聚合物动力学.但Lin等[106]发现,吸引二氧化硅纳米粒子对归一化的聚甲基丙烯酸甲酯(PMMA)扩散影响不是很大.为了描述归一化的聚合物扩散和受限参数关系,Meth等[107]提出了排除体积模型,该模型中聚合物链被假设为一定尺寸的球体,并以扩散的方式通过柱状孔道.该理论模型发现,球体扩散的减小和对应的排除体积有关,并且能捕捉到低纳米粒子体积分数体系(聚合物尺寸和纳米粒子表面之间间距满足条件ID/2Rg>2)中聚合物的扩散行为[102,106].但在高纳米粒子体积分数下,该理论模型高估了实验测得的聚合物扩散系数,这主要是因为在由纳米粒子诱导的拥挤环境中,链扩散不仅依赖于纳米粒子的排除体积,也与聚合物链构象变化及链缠结密度等因素有关.纳米粒子表面接枝高分子链会造成纳米粒子附近有更广阔的界面区域,并且接枝链和非接枝链相互穿插.纳米粒子的“软”行为和“硬”行为可以通过调控接枝密度及接枝长度等参数实现.Choi等[105]研究了这类纳米粒子对聚合物链质心扩散的影响,图3(B)表明,归一化后的链质心扩散仍能满足类似的标度关系,与纳米粒子的“软”和“硬”程度关系不大.此外,归一化后的链扩散只有在ID/(2Rg)>20时才近似于1,表明接枝纳米粒子对聚合物有一个长程效应,与接枝纳米粒子表面的局部结构变化相关.此外,研究发现,温度的变化导致归一化的聚合物扩散和受限参数关系不能成功描述聚合物的链扩散行为,这和纳米粒子引起的聚合物熵位垒增加有关[108].大部分研究聚合物扩散的实验选择的纳米粒子尺寸远大于聚合物尺寸,意味着与聚合物链相比,纳米粒子几乎不运动.减小纳米粒子尺寸时,由于纳米粒子和聚合物局部尺寸之间可能存在的协同耦合性及聚合物链节可能在纳米粒子表面处发生一系列解吸附行为,因而聚合物链的扩散会变得更加复杂[109~111].近年来的实验研究结果表明[112],在一定体积分数下,半径0.9 nm的吸引纳米粒子能明显地抑制聚合物链质心和链节松弛,Rouse时间尺度内一系列吸附-解吸附事件导致纳米粒子扩散与聚合物动力学相耦合,造成聚合物链节尺度的摩擦增加,使聚合物链扩散降低了60%. Fig.3 Normalized tracer diffusion coefficients plotted against the confinement parameter for PNCs with different hard NP’s sizes(A)[104] and different effective NP’s sizes(B)[105] (A) Copyright 2012,Royal Society of Chemistry; (B) Copyright 2013,American Chemical Society. Fig.4 Reduced diffusion coefficient of the centers of mass(CM) of the chains as a function of the dynamic confinement parameter h/λd for different values of the NP diameter σN[117] Continuous line: Dp=Dp0[1-exp (-h/λd)].Inset: Dp/Dp0 as a function of h/(2Rg).Continuous and dash-dotted lines: Dp=Dp0{1-exp[-ah/(2Rg)]},with a respectively equal to 5.44 and to 3.22.Copyright 2018,American Chemical Society. 从分子动力学模拟角度来看,纳米粒子的加入及纳米粒子含量的增加均会导致聚合物链扩散系数变小[113,114].改变纳米粒子和聚合物作用势同样会影响聚合物链扩散.Desai等[20]发现,强吸引的纳米粒子能抑制非缠结链扩散行为,当纳米粒子体积分数达到10%时,链扩散系数降低了将近一倍.但排斥纳米粒子对聚合物链扩散的影响与纳米粒子含量有关: 纳米粒子含量低时,纳米粒子由于排斥势会促进聚合物链扩散; 纳米粒子含量高时,纳米粒子由于几何受限抑制聚合物扩散.与缠结聚合物链相比,非缠结聚合物链构象熵在纳米粒子作用下损失较小[115],这也使得纳米粒子体积分数低的体系中聚合物链扩散并不像实验测得的那样大幅度降低,归一化后的质心扩散大于实验结果[102,104].但当聚合物链处于拥挤环境,即ID/(2Rg)≤0.5时,模拟结果与实验结果类似.Kalathi等[116]通过粗粒化模拟发现,低纳米粒子体积分数(φ=10%)下,光滑纳米粒子没有显著影响链扩散,即大尺寸纳米粒子几乎不影响聚合物扩散,而小尺寸纳米粒子最多只提高归一化的聚合物扩散系数40%.从以上聚合物扩散变化的模拟结果可知,聚合物扩散强烈依赖于模拟体系的细节.Sorichetti等[117]也使用粗粒化模拟证实归一化后的聚合物扩散和受限参数的关系,但他们发现低温体系中对应的关系并不能成功地描述聚合物扩散(图4).Sorichetti等认为受限参数不是一个静态量,而是和温度、 数密度等热力学参数及模型细节相关的动态量.因此,Sorichetti等修正了聚合物扩散系数D和受限参数的关系,具体定义如下: (2) 式中,D0为纯熔体中聚合物扩散系数.式(2)能很好地捕捉到不同温度体系中聚合物慢动力学信息.Sorichetti等强调动态长度尺度λd即协同长度尺度,类似于过冷液体体系中的长度尺度,即聚合物链节逃出局部笼域所需要的空间重排长度尺度.但λd的严格物理意义不是非常清晰,同时λd和热力学等参数的关系需要进一步挖掘.此外,Sorichetti等发现该关系式也能描述纳米粒子的扩散行为,只是对应的λd等于纳米粒子的流体力学半径,与体系温度无关[117].非格子Monte Carlo模拟[118]进一步发现受限参数不仅依赖于温度,而且与固定纳米粒子的尺寸有关. Fig.5 φ as a function of NP radius(R) with the symbols representing simulation data[126] Copyright 2019,American Institute of Physics. 聚合物包含多级长度尺度和时间尺度,表现出极其丰富的动力学行为[119,120].Rouse理论[121]认为,不同长度尺度之间的动力学满足一定关系.在聚合物纳米复合体系中,纳米粒子的存在可能会破坏聚合物不同尺度之间的动力学关系,这主要与聚合物纳米复合体系的多种因素相关,包括纳米粒子的强弱作用势[21]、 纳米粒子的尺寸大小及纳米粒子的聚集态[94,122]等.模拟研究发现,聚合物动力学松弛是否满足Rouse行为与模拟设置的截断半径及纳米粒子体积分数有关[123].纳米粒子的体积分数不同,对应的聚合物动力学行为不同.在低纳米粒子体积分数下,聚合物同时“遇到”2个纳米粒子以上的概率很小,并且聚合物链节可能会暂时性地停留在纳米粒子表面(不包括极强吸引纳米粒子),因此,处于不同长度尺度的聚合物受纳米粒子影响的概率相等.但随着纳米粒子体积分数增加,处于不同长度尺度的聚合物逐渐受限,表明分别处于大、 小尺度的聚合物动力学会受到不同的影响[116,124].耗散粒子动力学(DPD)模拟结果[125]表明,虽然纳米粒子减慢了处于不同长度尺度的聚合物松弛,但在低纳米粒子体积分数下,聚合物仍旧遵守Rouse行为,而在高纳米粒子体积分数下,由于纳米粒子强受限效应,造成处于不同长度尺度的聚合物链节困于不同的环境中,对应的聚合物松弛严重偏离于Rouse行为.近年来,Sun等[126]通过粗粒化模拟方法也观察到类似的行为,同时发现,处于整链尺度的聚合物松弛和处于链节尺度的动力学松弛的去耦合行为能很好地解释整链动态异质性的非单调性,并且动态异质性的非单调转变可以用式(1)粗略评估(图5). 与非缠结聚合物相比,缠结聚合物体系除链自身的Kuhn长度和链尺度外,还引入了管道直径.纳米粒子尺寸和管道直径大小严重影响着聚合物动力学行为.在无热弱吸引模型体系中[127](图6),纳米粒子对非缠结聚合物动力学的影响与Schneider等[128]实验所得到的结果相似.当纳米粒子尺寸小于聚合物缠结网络尺寸时,纳米粒子就像溶剂一样起到稀释作用,能够加速链节摩擦松弛,“溶胀”聚合物管道直径; 当纳米粒子尺寸大于1/2的缠结网络尺寸时,有效的链节松弛不受低体积分数的纳米粒子影响,而链缠结在高纳米粒子体积分数作用下降低.此外,在无热实验体系中,小尺寸金属氧化物纳米粒子能促进聚合物链解缠结和管道“溶胀”,但聚合物动力学松弛不偏离Rouse行为,而且改变纳米粒子尺寸不会影响聚合物Rouse动力学行为[129].Schneider等发现[128],不同含量的纳米粒子对聚合物动力学的影响不同,低纳米粒子含量的聚合物缠结到高纳米粒子含量的纳米粒子强受限.粗粒化分子动力学模拟研究了这个转变过程中的聚合物动力学变化,他们发现,聚合物缠结效应主导聚合物动力学时,纳米粒子加入会加速聚合物动力学松弛; 相反,当纳米粒子受限主导整个聚合物纳米复合体系时,聚合物动力学松弛变慢[130].此外,从聚合物缠结效应到纳米粒子受限效应,体系有效管道直径随着纳米粒子体积分数单调减小. Fig.6 Normalized effective relaxation times of p-th mode for chains in nanocomposites for different NP sizes at φNP=0.1[127] (A) N= 40; (B) N=100; (C) N=400.(D) Effect of NP loading for N=400,σNP=10σ(Closed triangles correspond to σNP=10σ in N=500 at similar NP loading from ref.[130],Copyright 2012,American Physical Society).(E) Corresponding plot for the stretching exponent βp. (A—E) Copyright 2015,Royal Society of Chemistry. 尺寸足够小的纳米粒子会塑化聚合物基质的性质[111,131,132],但在固定纳米粒子体积分数体系中,减小纳米粒子尺寸会增加纳米粒子的界面层从而减慢聚合物动力学松弛[133].因此,可能存在一个最优化的纳米粒子尺寸,对应复合体系性质会发生巨大变化[134].Volgin等[135]和Kropka等[136]研究了小尺寸吸引纳米粒子(直径小于2 nm)对聚合物性质的影响,结果表明小尺寸纳米粒子能大幅度地改变聚合物不同尺度的动力学松弛、 玻璃化转变温度及脆性[137].Composto等[112]发现,小尺寸吸引纳米粒子能极大地抑制聚合物扩散和链节松弛,但这种抑制行为来源于纳米粒子的焓吸引,不同于尺寸较大纳米粒子所引起的排除体积效应和熵效应.Cai等[111]指出,非黏性纳米粒子在聚合物基质中的运动取决于双方的不同长度大小,一定尺寸下的纳米粒子和聚合物在中间时间区域会共享双方的长度尺度与时间尺度,对应的动力学也相互关联,相互影响. Fig.7 Schematic of one sticky nanoparticle in a polymer melt for R>Rg(A),R≪Rg(B) and the “vehicle” mechanism(C)[138] Copyright 2018,American Chemical Society. 为了防止纳米粒子发生团聚,人们通常对纳米粒子进行一定的修饰或增加一定的吸引强度,但这样的措施往往复杂化纳米粒子界面处的性质.虽然结构因素的多样性使人们难以对聚合物纳米复合体系中聚合物不同尺度动力学变化行为达成共识,但扰动聚合物性质的纳米粒子扩散取得了重大的进展.Yamamoto等[138]基于动态键逾渗理论框架预测了纳米粒子运动的2个微观机理(图7): 核壳模型和媒介(Vehicle)模型,以此来研究聚合物熔体中吸引纳米粒子扩散行为.其中核壳模型是基于纳米粒子半径(R)大于聚合物回转半径(Rg)的情况,在该模型中,链节会吸附在纳米粒子表面,进而形成有效半径Reff~R+Rg的紧密层(阴影黑色层); 媒介模型是基于纳米粒子和吸附链节的协同运动情况,在该模型中,纳米粒子将吸附链节当成传播介质,初始跟随吸附链节一起运动[图7(C)中的红圈],经过一定时间τdes以后,局部吸附链节解吸附,纳米粒子就会去寻找下一个传播介质媒体[图7(D)中的绿圆圈].这些模型的建立为研究聚合物纳米复合体系中聚合物与纳米粒子多尺度动力学提供了非常有效的参考. 聚合物纳米复合体系可以被认为由本体相和界面相两部分组成,两者是相互竞争的关系.一些研究发现,纳米粒子附近存在着“死区”[76,93,139],并且这些“死区”的存在是造成复合体系高模量的主要原因[140,141].更多的研究[68,80,96,142~144]指出,处于界面层的聚合物结构和动力学呈现一定的梯度分布,该梯度分布的强弱依赖于纳米粒子的作用强度和纳米粒子表面粗糙度.而且界面处聚合物梯度状的动力学行为与自身动态异质性、 脆性及玻璃化转变温度(Tg)等紧密相关[80].另一方面,Tg能反映聚合物最基本的性质,与聚合物链节运动及松弛有关.纳米粒子不同的作用强度或纳米粒子的强受限会影响Tg变化[23,145,146],一般认为强吸引的纳米粒子能提高Tg,而弱吸引或排斥纳米粒子会降低体系Tg.但许多实验研究指出,强吸引纳米粒子几乎不影响聚合物Tg的变化[147].Sokolov等[70,94]的研究表明,不同类型的氧化纳米粒子对聚合物的Tg、 链节松弛及聚合物脆性影响非常弱,并且纳米粒子界面的链松弛慢于本体相中的聚合物链松弛几个数量级[69,122].为了解释实验中存在的争议,Kumar等[67]使用粗粒化模拟方法研究了纳米粒子不同作用强度对聚合物Tg的影响.他们发现,当纳米粒子吸引强度大于聚合物作用势时,界面聚合物会“覆盖”纳米粒子表层,造成本体区的链动力学和Tg变化不受纳米粒子作用强度影响,与先前实验中报道的关于纳米粒子不影响聚合物Tg的结论一致.随后,Starr等[148]发现,纳米粒子尺寸变小会降低界面层聚合物动力学的影响程度,但会大幅度地影响聚合物的Tg变化,这主要与纳米粒子尺寸变小导致的纳米粒子平均间距变小进而引起纳米粒子界面层相互重叠有关[图8(A)].同时,他们强调了在不同空间区域中纳米粒子附近界面效应的影响,在极低体积分数体系中,当聚合物和纳米粒子之间的作用强度超过本体中聚合物之间的作用强度时,纳米粒子附近的吸附链节动力学和聚合物基质动力学之间是去耦合的,体系Tg几乎不发生改变[图8(B)]; 当纳米粒子数目增加到局部聚合物链和纳米粒子发生“桥接”时,界面聚合物发生的“桥接”会引起体系Tg增加[图8(C)]; 进一步增加纳米粒子体积分数直到纳米粒子附近的界面区域相互重叠,此时的Tg与纯熔体的Tg相比发生巨大的变化[图8(D)][148].这些变化说明界面层性质和本体层性质之间的竞争决定着整个复合材料最终性能. Fig.8 Schematics of the different regimes for interfacial effects of the NP (A) The dilute regime.(B) The “bridging regime,” where the separation of the NPs allows the interfacial chains to bridge.(C) The interfacially dominated regime.The value of r/Rg for d=3.3σ,d=6.6σ,and d=10.0σ is r/Rg=3.3/2.16=1.52,r/Rg=6.6/2.16=3.05,and r/Rg=10.0/2.16=4.63,respectively.(D) The normalized change of Tg as a function of r/Rg.These data are gathered from Refs.[70,94,122,137,149,150].To estimate the mean face-to-face separation r between NPs,we use the expression r/d=(φmax/φ)1/3-1[151],where φmax is the maximum filling fraction(φmax≈0.7),d is the NP diameter,and φ is the NP filling fraction[148].Copyright 2018,American Physical Society. 随着社会的进步和科技的飞速发展,人们对高分子材料性能化和功能化的要求越来越高,对优异高分子材料的需求越来越多.聚合物纳米复合材料由于极其丰富的性质成为了当前以及未来社会最受瞩目的材料之一.然而由于聚合物纳米复合材料内部因素的多样性及复杂性,人们很难精确地去调控复合材料的性能.例如纳米粒子作用强度、 纳米粒子形状、 纳米粒子的分散性、 纳米粒子的多级结构、 纳米粒子与聚合物的各个特征长度尺寸比、 聚合物拓扑结构及聚合物链刚性等均会影响聚合物纳米复合材料的结构及动力学性质,从而进一步影响复合材料的力学性质、 流变性质及其它一些重要的性质.经过近几十年的发展,人们对聚合物纳米复合材料的结构与动力学等已经有了一定程度的了解.本文主要从计算模拟和实验角度并结合相关理论系统性总结了聚合物结构、 聚合物扩散及聚合物多尺度动力学相关研究进展,详细阐述上述因素对它们的影响规律.虽然这些研究能够在一定程度上加深对聚合物纳米复合材料结构和动力学的认知,但目前在聚合物纳米复合材料中仍存在着很多尚未解决的问题,如多个纳米粒子影响下聚合物构象和聚合物动力学、 动态异质性及流变的关系、 聚合物纳米复合材料玻璃化转变温度变化的规律及不同长度尺度的动态异质性变化与纳米粒子之间的关系等.因此,希望通过本文能够吸引更多科研人员关注聚合物纳米复合材料的结构和动力学信息,给聚合物复合材料的设计和性能优化提供更多的理论支持.1.2 界面层结构

2 聚合物扩散
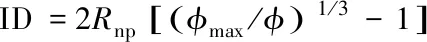
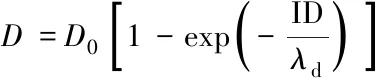
3 聚合物多尺度动力学
4 总结与展望