计及分布式光伏有功削减的配电网全局电压综合优化策略

靳 伟，王文宾，陈 岩，张 俏，赵 静，王 宁,*

(1. 国网河北省电力有限公司 邢台供电分公司, 河北 邢台 054001;2. 燕山大学 电气工程学院, 河北 秦皇岛 066004; 3. 河北交通职业技术学院 电气与信息工程系, 河北 石家庄 050035)

0 引言

随着光伏渗透率的提高，分布式光伏(Distributed Photovoltaic，DPV)出力的随机性和不确定性以及与负荷功率的不匹配，使得配电网电压波动加大，电压越限问题更加突出[1-3]。传统光伏电源通常按单位功率因数和最大功率跟踪控制方式工作[4]，仅发挥了光伏电源的有功发电功能。IEEE1547修订方案及我国分布式电源并网技术要求(GB/T 33593—2017)等规定分布式电源(Distributed Generation，DG)应主动参与配电网电压调节，根据电压和功率需求调整输出的有功、无功功率。新型光伏并网逆变器基本具备有功、无功远程调节控制功能[5-6]。DPV参与调压具有响应快速、无功双向可调、无机械磨损等多方面优势，对解决高密度光伏接入电网的电压问题具有重要作用。

含分布式电源配电网电压控制目前主要采取分散自治控制、分布式控制和集中控制三种策略。分散自治策略[7-9]依据本地量测信息对DG及其他无功设备进行自治控制，其优点是无需信息通信、配置灵活、实时性强。但分散自治策略由于缺乏整体协同性，全局电压控制能力有限。文献[8-9]提出几种依据并网点电压是否越限而采取的DG有功-无功协调工作模式；文献[10-11]提出通过削减光伏有功出力来防止电压越限的调压策略，但仅基于本地信息，不能从全网角度最小化削减有功。分布式控制策略[12]以本地智能控制器为节点建立通信联络，控制器间相对自治又相互协同，形成对等关系的网络控制系统。集中控制策略采用主从结构，通过控制中心优化控制全网电压水平，具有调控范围广、调压效果好的优势，技术应用较成熟。文献[13]提出DG与电容器、变压器相结合的无功优化策略。文献[14]考虑到光伏有功、无功之间的耦合性，协调优化配电网中的可控有功、无功资源来调节电压，采取日前优化、在线修正相结合的多时间尺度优化控制方案。文献[15]针对DG接入配电网可能引起的电压越限问题，建立了综合优化DG无功出力和无功补偿设备的配电网长时间尺度无功优化模型。文献[16]以可控DG、储能、分段开关和无功补偿设备等为调控手段，以配电网运行成本及运行越限风险最低为目标，建立主动配电网日前优化模型。文献[17]协调优化DG、柔性负荷、储能、补偿电容器及变压器，以配电网运行成本最小为目标建立多时间尺度有功-无功协调优化模型。

光伏逆变器在大多数运行时间具有较大的剩余容量，只有在天气条件非常好的极小时间段内其有功出力可能接近满容量。因而在剩余容量不足的情况下，通过适当削减有功来满足电压合格是一种经济合理的手段。如何从全网角度最小化削减有功是需要解决的问题。本文提出一种考虑分布式光伏有功削减策略的配电网电压控制方法，依据电压是否越限分步实施优化策略。首先在DPV按最大功率跟踪输出有功的前提下利用逆变器剩余容量进行无功优化，使全网电压水平总体最优；若优化后仍有节点电压越限，则以全网电压合格为约束建立光伏有功削减模型，得到满足电压合格的最小有功削减方案，并重新进行无功优化，得到全网最佳电压分布。采用复仿射方法划分时段建立不确定模型，利用Ybus潮流计算与线性递减权重粒子群(Linear Decreasing Weight Particle Swarm Optimization，LinWPSO)算法相结合的方法对上述优化模型进行求解。

1 光伏与负荷复仿射模型

光伏的有功出力随天气情况波动，负荷功率消耗随时间不断变化。因此，在制定DPV并网优化策略时需要考虑两者的不确定性出力对配电网电压的影响。其中，应用较广泛的是基于概率分布的机会约束规划方法[18]，但其无法根据次日天气情况的不同改变光伏输出。本文采用复仿射算法建立各时段光伏电源和负荷不确定输出模型。仿射数学方法不但能够简便地表达这种不确定性并且在潮流计算时能有效缩小潮流解范围，兼顾解的完备性和准确性。

1.1 DPV复仿射模型

光伏有功出力区间主要和光照强度的波动有关，而光照强度和天空中云层的变化有很大关系[19-20]。根据气象信息可获得各时段天气状况，利用仿射和区间的转换公式[20]，得到云层系数和大气层外光照强度的仿射表达式为

(1)

(2)

1.2 负荷复仿射模型

电力负荷输出具有不确定性与时序变化的特点。因此，采用复仿射方法建立各时段的负荷有功和无功输出模型为

(3)

(4)

2 光伏逆变器的电压控制策略

2.1 DPV调压的主从分散协调控制

本文DPV调压控制策略的思路是，首先逆变器的本地控制器按指令值实时闭环调节逆变器有功、无功输出，指令值由全局优化策略给定；以配电网全局电压优化为目标对无功及有功削减量等光伏运行指令值进行全局优化决策，并将优化指令值通过分布式网络发送给本地控制器；以次日负荷和光伏预测值为参考，做出15 min为一个时段的指令优化结果，作为本地控制器次日各时段运行指令。因此本文核心工作就是通过全局优化实现多个光伏电源协调配合运行，形成全局-本地两级控制的主从分散协调控制系统。DPV对配电网进行电压控制的分散协调控制结构如图1所示。

图1 光伏调压全局/本地分散协调控制系统
Fig.1 Global/local decentralized coordinated control system based on photovoltaic voltage regulation

2.2 DPV无功-有功削减协调优化策略

电压合格率是电力系统的重要考核指标，电压越限会给电网和用电设备构成威胁。《电能质量供电电压偏差(GB/T 12325—2008)》中对各种电压等级的电压偏差允许值做了规定，其中要求20 kV及以下电压等级的供电电压偏差不超过标称电压的±7%。《供配电系统设计规范(GB 50052—2009)》规定用电设备端子处电压偏差允许值宜符合±5%。DPV的接入加大了电压越限风险，DPV通常采用最大功率点跟踪控制模式，保证光伏有功出力最大化。但如凭借无功调压手段仍无法控制电压在上述标准范围内时，为保障电网安全运行，适当削减有功出力是必要的。本文提出一种以电压合格为条件，最小化削减有功为原则的DPV无功与有功削减协调优化调压策略。首先使分布式光伏按最大功率跟踪方式输出有功功率，并利用逆变器剩余容量进行无功电压调节，使电压最优；若以剩余容量为优化空间进行无功优化后，电网仍有电压不合格节点，则通过优化手段最小化削减逆变器有功输出，从而使全网电压合格；同时对削减出的逆变器容量再次进行无功优化，以进一步改善电压合格水平。具体步骤如下：

1) 在DPV最大化输出有功的前提下利用逆变器剩余容量提供无功功率，建立以全网总电压偏差最小为目标函数的静态无功优化模型，优化变量为光伏无功出力仿射量。

2) 若优化后仍有节点电压越限，则在第一步无功优化结果的基础上以全网电压合格为约束，光伏总有功出力仿射值最大为目标函数建立有功削减优化模型，得到满足电压合格的最小有功削减方案。

3) 根据有功削减值，计算出逆变器新增剩余容量，求出逆变器无功输出范围，判断节点电压是否满足约束要求。若不满足条件，重新进行无功优化；若满足条件，则输出优化结果。

上述步骤可表示成如图2所示的DPV参与的无功-有功削减协调优化策略流程图。

图2 DPV参与的无功-有功削减协调优化策略流程图
Fig.2 Flow chart of reactive-active curtailment coordination optimization strategy participated with DPV

3 DPV无功-有功削减优化建模

DPV逆变器总容量除了传递有功功率外，其剩余容量可用于电压无功控制，在剩余容量限值范围内具体的无功需求则取决于电压无功优化。本文电压无功优化的决策变量是各逆变器输出无功功率或有功削减量，优化的目标是电压最优。无功功率及有功功率对电压的影响关系通过潮流方程来反映。

3.1 目标函数

以各时段全网总电压偏差最小为目标函数：

(5)

式中，Uit为t时段节点i的电压区间中值；U0为节点电压期望值；n为系统节点数。

以光伏电源总有功出力仿射值最大为目标函数：

(6)

目标函数F1和F2分别对应于第2节步骤一和步骤二所述目标函数。

3.2 约束条件

1) 等式约束

光伏出力、负荷功率、补偿装置无功功率应满足如下潮流方程：

(7)

(8)

2) 节点电压约束

[Uit]⊆[Umin，Umax],

(9)

式中，[Uit]为时段t内节点i的电压幅值区间，i=1,2,…,n；Umax和Umin分别为满足运行要求的电压上、下限值。

3) 逆变器运行约束

DPV发出的无功功率由光伏逆变器的运行容量和光伏输出的有功功率共同决定，即

(10)

式中，Qft为时段t内光伏电源f无功出力；S、Pft分别为光伏并网逆变器安装容量和光伏削减后的有功出力值。

4 模型求解方法

Ybus高斯迭代潮流计算对初值要求低，不需要快速解耦且收敛性不受R/X限制[21]。线性递减权重粒子群(LinWPSO)算法是一种改进粒子群算法[22]，算法在迭代前期加强全局搜索，避免在局部最优解附近徘徊，加快粒子群算法的收敛速度；在迭代后期对局部进行细致地搜索，提高解的精度。因此，本文采用Ybus潮流计算与LinWPSO相结合的算法对优化模型进行求解。

4.1 仿射参与的无功优化模型求解流程

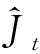
4) 将随机产生的种群个体以及步骤(3)得到的仿射量代入Ybus潮流计算得到各个节点电压区间值[Uit]，选取各个节点电压区间的中值Uit与电压额定值U0的偏差之和最小作为适应度函数，找出各个粒子个体最优值pbest和全局最优值gbest。

5) 更新每个粒子的速度和位置，更新惯性权重，再次进行Ybus潮流计算，得到每个粒子的适应度值，更新种群位置和速度进行迭代。

6) 判断是否达到最大迭代次数，若满足条件，则输出最优变量值，否则返回步骤4)。

4.2 有功削减优化模型求解流程

有功削减优化模型求解过程是指设定节点电压满足区间约束，然后将静态无功优化结果，光伏有功出力变量代入Ybus潮流计算，并通过LinWPSO迭代寻优得到削减后的光伏有功出力值。具体求解流程如图3所示。

5 算例分析

选取IEEE33节点系统为算例验证本文所提优化策略的有效性。系统拓扑结构如图4所示，电压等级为10 kV。在节点0和1之间接入一台有载调压变压器，变比范围为0.95～1.05，共9档，调节步长为1.25%。在7节点和12节点分别接入光伏电源，考虑到馈线接入形式的光伏电源容量一般在百kW到1 MW之间，本文设每个光伏电源的装机容量为500 kW。在17节点和32节点分别接入8组无功补偿电容器，单组容量为150 kvar。模型求解算法参数设置：时段数为24，LinWPSO的种群规模为50，学习因子c1=c2=2.0，维数D=5。惯性权重ω=0.8，ωmax=0.9，ωmin=0.4，ω在[0.4，0.9]之间代数线性递减，最大迭代次数T=60。考虑到现代电网中新型敏感负荷对供电质量要求的提高，且由于10 kV电网直接连接用户端，结合相关标准的限值规定，算例中电压阈值取±5%。

图3 有功削减优化模型求解方法流程图
Fig.3 Flow chart of active reduction optimization model solution

图4 IEEE33节点系统结构图
Fig.4 IEEE33 node system structure diagram

本文选取一天的光伏电源出力和负荷进行分析。光伏电源和负荷的输出功率复仿射模型由1.1节和1.2节已知，由实际气象信息得到不同天气状况下的云层系数仿射量，如表1所示。

表1 云层系数仿射量
Tab.1 Affinity of clouds coefficient

天气状况云层系数仿射量晴J^=0.95+0.05εit多云转晴J^=0.80+0.10εit多云J^=0.60+0.10εit阴转多云J^=0.40+0.10εit阴J^=0.25+0.05εit雨或雪J^=0.15+0.05εit

各个时段光伏电源有功出力仿射量计算式为

(11)

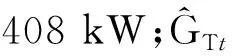
进行潮流计算时需要考虑负荷数据的不确定性。本文假设同一时段内的负荷出力不确定率基本一致，即δt相同，然后根据式(3)、(4)计算得到各个时段不同节点负荷的复仿射量。

5.1 无功优化结果分析

在已知DPV和负荷复仿射输出量的基础上，协调控制光伏逆变器、有载调压变压器和无功补偿电容器进行无功优化。优化结果说明计及光伏无功调控能力的无功优化可以提高电压水平。但在第11～14时段内部分节点发生电压越限问题，如图5所示。图5(a)～(c)分别为11～12、12～13和13～14时段各个节点电压幅值区间。

导致电压越限的原因是该时段光伏有功输出较大，甚至超过装机容量的70%，使得无功调压有效利用容量减小，即使逆变器全部剩余容量用于无功调压也无法将节点电压调至正常区间内。

图5 无功优化后11-14时段电压幅值区间
Fig.5 Voltage results of the 11-14 period after the reactive power optimization

5.2 DPV有功削减优化结果分析

进行有功削减优化的目的是在电压合格的前提下保证光伏电源的最大化消纳。选取不满足要求的11～14时段无功优化结果，根据DPV参与的无功-有功削减协调优化模型进行光伏电源有功削减优化，所得优化结果如表2所示。

表2 光伏电源有功出力值
Tab.2 Photovoltaic power active output valuekW

时段初始值PPV1PV1有功消减值PPV2PV2有功消减值11～12327296313032412～13340300403151513～143322983431220

从表2可知，有功削减优化后得出的输出值相比于光伏电源初始中值削减了20 kW到40 kW不等，其中接入7节点的光伏1有功削减值比接入12节点的光伏2削减值要多，这说明光伏1对电压的影响程度要大于光伏2。因此，在具体实施有功削减过程时可优先对光伏1进行操作。

5.3 无功可调容量增加后优化结果分析

将表2中的数据代入式(10)求解得到新增的光伏无功出力范围，重新进行无功优化，得到11～14时段的光伏电源无功出力值，如表3所示。优化后的电压结果如图6所示。

表3 光伏电源无功出力值
Tab.3 Photovoltaic power reactive output value kvar

时段QPV1maxQPV2maxQPV1QPV211～12403398398.12392.2812～13400388395.29385.5613～14401391396.49387.22

由表3可知，光伏逆变器的新增剩余容量全部用于无功优化调压，调用最小的无功容量实现电压不越上限。

图6 无功-有功协调优化后11～14时段电压幅值区间
Fig.6 The voltage result of the period 11～14 after the active-reactive power coordination optimization

从图6可以看出，图5中不满足要求的节点电压，经光伏有功削减、释放出更多容量进行无功优化调压后，全部落在[1.01, 1.05]区间内。因此，本文提出的无功-有功削减协调优化控制策略可有效解决无功容量不足引起的电压越限问题，并保障光伏最大化输出。

5.4 优化治理前后的结果对比

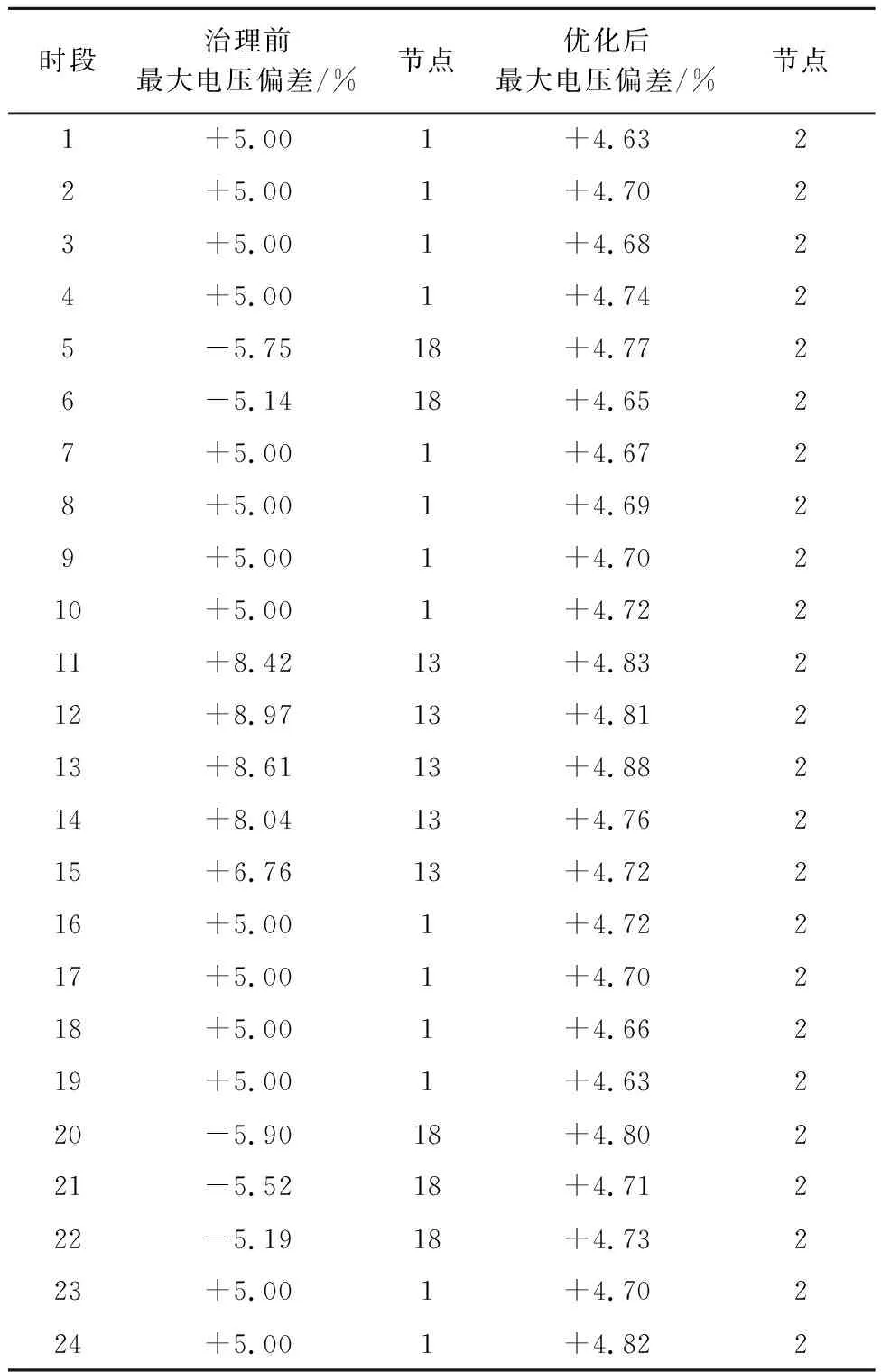
就本文所选算例而言，在时段1～10和时段15～24仅通过光伏逆变器剩余容量、有载调压变压器和无功补偿电容器组进行无功优化调压，在时段11～14通过无功-有功协调优化调压，两者相互配合最终使得全网电压合格且电压偏差最小。表4给出了24时段本文策略优化后节点电压最大偏差与治理前电压最大偏差的对比情况。可见治理前最大电压偏差为8.97%，而优化治理后最大电压偏差为4.88%。

表4 24时段节点电压最大偏差对比
Tab.4 Comparison of maximum node voltage deviation during 24 hours

时段 治理前最大电压偏差/%节点 优化后最大电压偏差/%节点1+5.001+4.6322+5.001+4.7023+5.001+4.6824+5.001+4.7425-5.7518+4.7726-5.1418+4.6527+5.001+4.6728+5.001+4.6929+5.001+4.70210+5.001+4.72211+8.4213+4.83212+8.9713+4.81213+8.6113+4.88214+8.0413+4.76215+6.7613+4.72216+5.001+4.72217+5.001+4.70218+5.001+4.66219+5.001+4.63220-5.9018+4.80221-5.5218+4.71222-5.1918+4.73223+5.001+4.70224+5.001+4.822

由表4可知，当光伏接入配电网后，在5、6时段和20～22时段，出现电压越下限的情况，最大电压偏差发生在18节点。在11～15时段，由于光伏出力的不断增加，电压越上限，最大电压偏差发生在13节点。采用本文提出的有功削减、释放无功控制策略以全网总电压偏差最小为目标进行优化后，24个时段的节点电压全部合格。

6 结论

本文提出一种考虑分布式光伏有功削减的配电网日前电压协调优化方法，依据电压是否越限建立了DPV无功优化模型和有功削减优化模型，制定了DPV无功和有功削减相协调的优化策略。本文方法优先利用逆变器剩余容量进行电压无功优化，当不能满足电压要求时，从全网角度最小化削减DPV有功输出，保障了高渗透配电网在复杂不确定运行场景下的电压安全和新能源消纳。采用复仿射方法建立各时段功率输出不确定模型，依据次日天气具体情况给出可调范围，使控制策略能够更好适应优化场景的不确定性。