风筝发电机飞行轨迹分析及优化
2020-05-18肖小丽詹杰
肖小丽 詹杰


摘 要:在可持续发展绿色能源开发中,风力发电一直备受人们的关注。经过长期的试验表明,传统风力涡轮机发电系统制造成本昂贵、维护运营较难。而高空风筝发电系统成本更低、发电效率更高,更有利于长期发展。高空风筝发电系统单位时间内的发电功率是我们评价一个系统好坏的关键指标,为了使风筝发电系统获得的发电量达到更大,文章将对风筝发电机的飞行轨迹进行研究优化。
关键词:风筝发电;圆形轨迹;轨迹优化
中图分类号:TM31 文献标志码:A 文章编号:2095-2945(2020)14-0016-02
Abstract: In the sustainable development of green energy development, wind power generation has been concerned by people. The long-term test shows that the traditional wind turbine power generation system is expensive to manufacture and difficult to maintain. The high-altitude kite power generation system has lower cost and higher power generation efficiency, which is more conducive to long-term development. The power of kite power generation system in unit time is the key index for us to evaluate the quality of a system. In order to make the power generated by kite power generation system reach a higher level, this paper will study and optimize the flight path of kite generator.
Keywords: kite generator; circular trajectory; trajectory optimization
引言
風筝发电机发电过程由牵引阶段和回收阶段构成。[1]在牵引阶段,风筝沿一定轨迹在强横风力的作用下反复飞行,并拉动缠绕在滚筒上的系绳进行发电。当系绳卷出长度达到最大时,为实现系统的动力循环需将风筝拉回到牵引阶段初始长度。在回收阶段,发电机发电带动滚筒回绕系绳,风筝被拉回为下一次循环做准备。牵引阶段通过系绳的牵引力带动电动机运转使得发电系统产生电能,而回收阶段需要消耗牵引阶段产生的一部分电能,通过周期性循环使得产生的电量差不断积累以供人们的生活需求。
在牵引阶段,风筝在高空中的飞行主要有圆形轨迹[2]和八字形轨迹[3]两种,即随着系绳的不断放出风筝以螺旋圆形或者八字形轨迹重复飞行。为了使得回收阶段消耗的能量减小,回收方式有滑翔返回方式、垂直轨道返回方式、逆风轨道返回方式三种。[4]滑翔返回方式是在牵引阶段结束时,减小风筝的有效表面积来改变风筝的气动升力,从而减小系绳卷回过程中所需要的牵引力。即通过控制收回两根系绳中的一根产生长度差使风筝表面与系绳在同一直线上。垂直轨道返回方式是在牵引阶段结束时,控制牵引风筝的两条系绳长度差使风筝不断升高直至风筝平面与地面平行,即风筝表面与风速方向平行。此时,风筝表面所受空气动力减小,可以通过卷回系绳使风筝垂直向下运动直至到达牵引过程系绳初始长度。逆风轨道返回方式是在牵引过程结束时,减小风筝的攻角使风筝所受空气动力降低。同时提高地面滚筒的卷回速度,使风筝处的气流减小,从而使得系绳牵引力也相应减小。风筝逆风沿低轨道返回,要使攻角不能低于最低值,否则容易倒塌。圆形轨迹由于其拓扑结构简单在实践中经常被用到,因此下文选择圆形轨迹行进优化研究。
1 理论基础
风筝发电系统的最终目标是获得最大净发电量,即尽量使得系绳卷出阶段获得最大电能,同时使得系绳卷回阶段消耗最少的电能。[5]因此针对不同的阶段,提出了不同的目标函数。
3 结束语
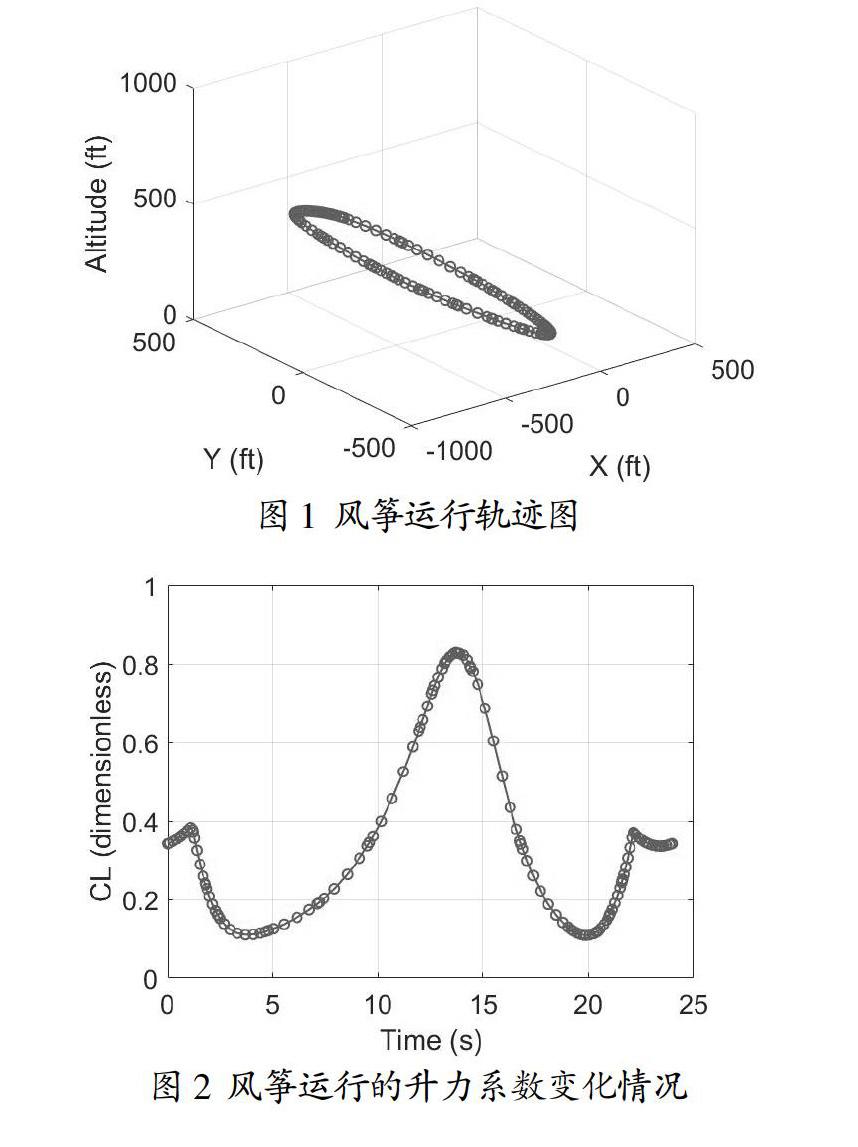
本文简单介绍了风筝发电机飞行轨迹的种类,并通过Matlab仿真优化了单个周期内的圆形轨迹,得到了相应的升力系数取值。由于风筝沿圆形轨迹飞行可能会出现系绳缠绕的不足,因此八字形轨迹研究具有重要的意义。通过圆形轨迹的优化研究为八字形轨迹的研究奠定基础。
参考文献:
[1]Wood T A, Hesse H, Polzin M, et al. Modeling, Identification, Estimation and Adaptation for the Control of Power-Generating Kites[J]. IFAC-Papers OnLine, 2018,51(15):981-989.
[2]Kheiri M, Nasrabad V S, Bourgault F. A new perspective on the aerodynamic performance and power limit of crosswind kite systems[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019,190:190-199.
[3]Erhard M, Strauch H. Control of towing kites for seagoing vessels[J]. IEEE Transactions on Control Systems Technology, 2012,21(5):1629-1640.
[4]Williams P. Optimal wind power extraction with a tethered kite[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. 2006:6193.
[5]Canale M, Fagiano L, Ippolito M, et al. Control of tethered airfoils for a new class of wind energy generator[C]//Proceedings of the 45th IEEE Conference on Decision and Control. IEEE, 2006:4020-4026.
[6]Patterson M A, Rao A V. GPOPS-II: A MATLAB software for solving multiple-phase optimal control problems using hp-adaptive Gaussian quadrature collocation methods and sparse nonlinear programming[J]. ACM Transactions on Mathematical Software (TOMS), 2014,41(1):1-37.
[7]Gong-Jian Y U, Shou-Yi L, Xun-Liang Y, et al. HP-RPM based trajectory optimization for hypersonic glide vehicle[J]. flight dynamics,2017,35(02):59-63.
[8]Pastor-Rodríguez A, Sánchez-Arriaga G, Sanjurjo-Rivo M. Modeling and stability analysis of tethered kites at high altitudes[J]. Journal of Guidance, Control, and Dynamics, 2017,40(8):1892-1901.
