二维H(div)和H(curl)空间到其迹空间的离散的拟范数等价定理

霍志鑫，王 猛，王园园，孔德志

(河北水利电力学院基础部，河北省沧州市重庆路1号 061001)

1 引入

刘勇翔等在文献[1]中的引理3.1中给出了H1(Ω)中离散的调和延拓定理，以及到其迹空间H1/2(∂Ω)离散的拟范数等价定理。Barbara I. Wohlmuth等在文献[2]引理4.3中给出了从Q0,h(Ω)空间到RTh(Ωi)空间的具有零散度的延拓定理。文中在此基础上利用类似的证明方法给出了相应迹空间H-1/2(∂Ω)到二维H(div;Ω)和H(curl;Ω)空间的离散的调和延拓定理证明，从而得到了二维H(div;Ω)和H(curl;Ω)空间到相应迹空间H-1/2(∂Ω)的离散的拟范数等价定理。这在理论分析和数值计算方法的设计中有很重要的作用。

文中，第二部分给出了二维H(div;Ω)空间到其迹空间H-1/2(∂Ω)的离散的拟范数等价定理，第三部分给出了二维H(curl;Ω)空间到其迹空间H-1/2(∂Ω)的离散的拟范数等价定理，第四部分给出了该定理在数值上应用的例子。

2 二维H(div;Ω)空间到其迹空间H-1/2(∂Ω)的离散的拟范数等价定理

首先，引入如相关记号。

(1)相关的连续空间及有限元空间

记

VΩ∶=H(div;Ω),VΩ,0∶=H0(div;Ω),

V∂Ω∶=H-1/2(Ω)

空间，H(div;Ω)∶=

(2)相关的能量模与图模

双线性型

双线性型

显然，能量模‖·‖a与图模‖·‖div等价。

(3)相关的离散调和延拓

(4)相关的迹空间

任给一个向量u∈H(div;Ω)，可以定义其边界∂Ω上的法向成分u·n，有如下引理(见文献[4]第一章的定理2.5)。

γn(Rnφ)=φ，∀φ∈H-1/2(∂Ω)

而且下面的格林公式成立，对于∀u∈H(div;Ω)，∀q∈H1(Ω)，有

这里等号右边这一项的积分可以理解为H-1/2(∂Ω)和H1/2(∂Ω)之间的对偶，称H-1/2(∂Ω)为H(div;Ω)的迹空间。

根据上述引理2.1中算子γn∶H(div;Ω)→H-1/2(∂Ω)的连续性，可得到如下离散的迹定理。

定理2.2 对于离散调和延拓Eh，有

其中，常数C与Ω的直径无关。

反之，可以得到如下离散的调和延拓定理。

定理2.3 存在与Ω直径无关的常数C，使得

证明:下面的证明类似于文献[3]的引理10.19和文献[2]的引理4.3。首先，对具有单位直径的结T证明相应的结论。考虑如下的Neumann问题:

(1)

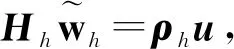
这里|f|是面f的面积。

由于divv=φ，从而有

=Cadiv(ρhu,ρhu)

这里εT严格正定并且依赖于T。

(2)

(3)

这里，利用式(2)以及逆不等式，得到

利用文献[3]中的引理B.20，得到

这里，∏h是在每一个面t∈T上到常函数空间L2的投影，并且

并且

≤Cht‖u‖1;t

那么

‖P‖H0(t)→H0(t)≤2;‖P‖H1(t)→H0(t)≤Cht

利用差值理论，有

即

从而，应用逆定理及式(3)，得到对于s<εT，有

所以

(4)

现在考虑直径为H的子结构Ω,利用对于具有单位直径的子结构T的结论式(4)，使用尺度伸缩技巧，得到以下结论:

其中，常数C与Ω的直径无关。

结合定理2.2和定理2.3，可得到迹空间H-1/2(∂Ω)到二维H(div;Ω)空间的拟范数等价定理。

定理2.4 存在与Ω的直径无关的常数C1，C2，使得

3 二维H(curl;Ω)空间到其迹空间H-1/2(∂Ω)的离散的拟范数等价定理

首先，引入相关记号。

(1)相关的连续空间及有限元空间

记

VΩ∶=H(curl;Ω),VΩ,0∶=H0(curl;Ω),

V∂Ω∶=H-1/2(Ω);

(2)相关的能量模和图模

双线性型

双线性型

显然，能量模‖·‖a与图模‖·‖curl等价。

(3)相关的离散调和延拓

(4)相关的迹空间

任给一个向量u∈H(curl;Ω)，可以定义其边界∂Ω上的切向成分u·t，有如下引理(见文献[4]第一章的定理2.11)。

→H(curl;Ω)使得

γt(Rt∶φ)=φ，∀φ∈H-1/2(∂Ω)

并且下面的格林公式成立。对于∀u∈H(curl;Ω)和∀q∈H1(Ω)，有

称H-1/2(∂Ω)为H(curl;Ω)的迹空间。

根据上述引理3.1中γt∶H(curl;Ω)→H-1/2(∂Ω)的连续性，可得如下的离散的迹定理。

定理3.2 对于离散调和延拓Eh，有

其中，常数C与Ω的直径无关。

如下引理见文献[3]中的引理A.20。

引理3.3 向量u=(u1,u2)属于H(curl;Ω)，当且仅当该向量属于H(div;Ω)。另外，

v·n=-u·t

根据上述引理3.3，如果Ω属于二维空间，则H(curl;Ω)空间中的向量与H(div;Ω)空间中的向量形成了一一对应，从而在H(div;Ω)空间中成立的结论，在H(curl;Ω)空间中同样成立，故结合定理2.3知，如下离散的调和延拓定理成立。

定理3.4 存在与Ω的直径无关的常数C，使得

结合定理3.2和定理3.4，得如下迹空间H-1/2(∂Ω)到二维空间H(curl;Ω)的拟范数等价定理。

定理3.5 存在与Ω的直径无关的常数C1，C2，使得

4 数值应用的例子

文中给出的定理在分析二维H(div;Ω)和H(curl;Ω)空间中具有Robin-Robin边界条件的最优的区域分解算法中，在理论上起到了关键性的作用[6]。该算法经过理论分析，得出预处理后的系数矩阵的条件数与网格的细度h无关，也就是收敛速度与网格的细度h无关，从而该算法就是最优的。如下给出了H(curl;Ω)空间中该算法的数值结果，H(div;Ω)空间中该算法的数值结果类似。

考虑下面的问题

(1)γ1=h,γ2=100时，迭代计算结果见表1、表2和图1。

表1 迭代时间(γ1=h,γ2=100)

表2 迭代数(γ1=h,γ2=100)

图1 迭代时间与迭代数(γ1=h,γ2=100)

(2)γ1=2h,γ2=100时，迭代计算结果见表3、表4和图2。

表3 迭代时间(γ1=2h,γ2=100)

表4 迭代数(γ1=2h,γ2=100)

图2 迭代时间与迭代数(γ1=2h,γ2=100)

(3)γ1=h,γ2=50时，迭代计算结果见表5、表6和图3。

表5 迭代时间(γ1=h,γ2=50)

表6 迭代数(γ1=h,γ2=50)

图3 迭代时间与迭代数(γ1=h,γ2=50)

(4)γ1=h,γ2=50时，迭代计算结果见表7、表8和图4。

表7 迭代时间(γ1=2h,γ2=50)

表8 迭代数(γ1=2h,γ2=50)

图4 迭代时间与迭代数(γ1=2h,γ2=50)