大跨连续刚构桥箱梁抗震分析与减震措施研究

2020-05-15蒋建军郑万山2唐光武2刘振宇

公路工程 2020年2期

蒋建军，郑万山2，唐光武2，刘振宇

(1.四川省公路规划勘察设计研究院有限公司，四川成都 610041； 2.招商局重庆交通科研设计院有限公司，重庆 400060)

0 前言

大跨径连续刚构桥的箱梁与主墩固结，箱梁采用挂篮悬臂施工法，施工期稳定性好，跨越能力强；主要材料为混凝土、钢筋和预应力钢材，造价经济；建成后，整体性好，抗震性能好，且主墩处无支座，耐久性好；通过调整桥墩截面型式和尺寸，可以适应不同地形、不同墩高，适应性强。大跨径连续刚构桥梁从上世纪中叶出现后，得到工程界的广泛认可和迅速发展，如1985年澳大利亚建成了主跨260 m的门道桥，1998年挪威建成了主跨298 m的Raft Sundet桥[1]；我国1997年建成了主跨270 m的虎门大桥副航道桥[2]，1999年建成了3孔主跨250 m的重庆黄花园嘉陵江大桥[3]，2006年建成了主跨330 m的重庆石板坡长江大桥复线桥[4]等。

简支梁桥、小跨径连续梁桥的梁体与桥墩之间设置支座，墩梁之间可发生相对转动、滑动等变形，地震作用时上部结构的地震力小，梁体一般不需进行抗震设计。连续刚构桥梁具有箱梁与主墩固结的特点，使得箱梁在地震作用下将会弯曲变形，产生较大弯矩和剪力，对箱梁抗裂及承载能力产生不利影响，应在抗震设计中给予重视。提高连续刚构桥抗震性能的技术措施主要有：①减轻上部结构重量，如采用空腹式组合结构[5-6]、波折钢腹板[7]、钢混组合体系[4，8]等；②优化桥墩型式，如薄壁墩、钢管混凝土格构柱[9]等；③设置减隔震装置，如拉索减震支座[10]、高阻尼隔震支座、粘滞阻尼器等。以往大跨径连续刚构桥的抗震研究主要关注点在桥墩，而对箱梁的抗震研究较少，在抗震设计中可能由于认识不足造成箱梁抗震性能不满足要求，需要在不中断交通的情况下采取有效的减震措施提高箱梁和主墩的抗震性能。

1 工程概况

某刚构+连续梁协作体系桥的桥跨布置为90+190+228+123+60(m)，桥宽13 m，荷载等级为公路-I级，其中1#主墩高32.5 m，2#主墩高102.6 m，3#主墩高101.6 m，4#辅助墩高44.2 m，两岸设U型桥台，墩台均采用桩基础，桥梁立面见图1。1#～3#主墩为双薄壁墩，4#墩为单薄壁墩，墩身均采用C50混凝土，主墩截面尺寸见图2、图3。箱梁为单箱单室截面，采用C55混凝土，标准截面尺寸见图4。该桥位于7度地震区，50 a超越概率10%时地震动峰值加速度为0.10g、特征周期为0.45 s。

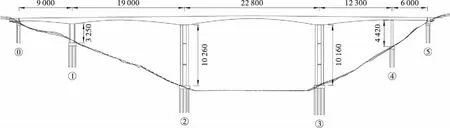
图1 桥梁立面图(单位:cm)Figure 1 Bridge vertical view(Unit:cm)

2 主墩墩型对箱梁抗震性能影响

大跨径连续刚构桥墩型式主要有3种：①独柱空心薄壁墩；②双空心薄壁墩；③双实心薄壁墩[1]。独柱空心薄壁墩和双空心薄壁墩的截面尺寸大，多用于高墩；双实心薄壁墩截面尺寸小，多用于矮墩。为研究主墩墩型对箱梁抗震性能影响，2#、3#桥墩分别采用独柱空心薄壁墩和双空心薄壁墩进行计算，同时双薄壁墩中间系梁道数分别取0道、1道、2道共3种情况。独柱空心薄壁墩按照截面面积等效设置，其截面尺寸见图5。

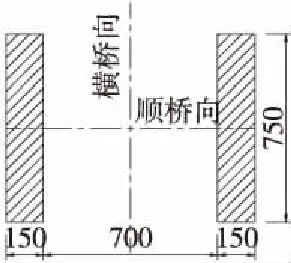
图2 主墩截面(单位:cm)Figure 2 No.1 main pier’s section(Unit:cm)

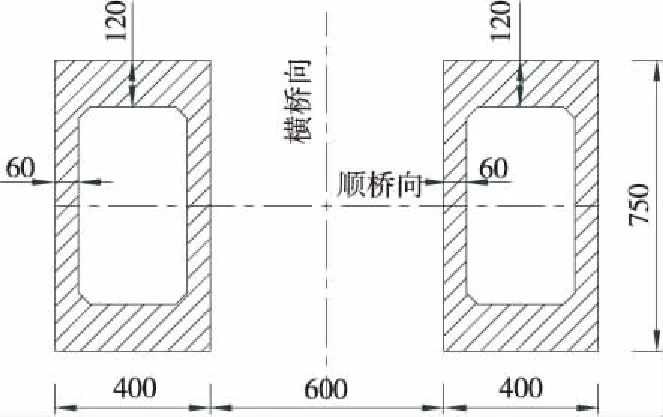
图3 2#～3#主墩双空心薄壁截面(单位:cm)Figure 3 No.2&3 main piers’ double hollow thin-walled section(Unit:cm)

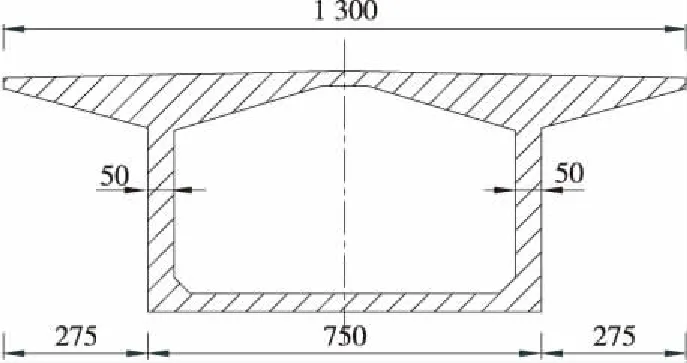
图4 标准箱梁截面(单位:cm)Figure 4 Standard box girder section(Unit:cm)

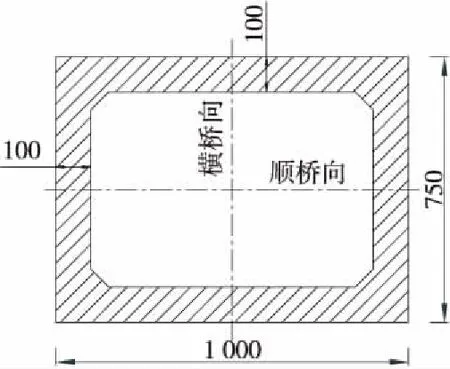
图5 2#～3#主墩独柱空心薄壁截面(单位:cm)Figure 5 No.2&3 main piers’ single hollow thin-walled section(Unit:cm)

采用有限元计算软件Midas Civil建模，主墩为独柱空心薄壁墩时计算模型见图6，为双空心薄壁墩(2道系梁)时计算模型见图7。由于考虑桩土作用对桥梁抗震有利[11]，为简化分析、便于研究，计算模型在承台底固结。辅助墩及桥台处均按照盆式橡胶支座考虑边界条件，进行振型分析和E1地震反应谱法计算(竖向设计加速度反应谱值为水平向的0.65倍)，对桥梁纵向整体抗推刚度、主要振型周期进行对比，结果见表1；选取2#墩处箱梁根部截面、2#墩顶与墩底截面进行弯矩响应对比，地震纵向输入时结果见表2，竖向输入时结果见表3。

图6 主墩为独柱空心薄壁墩时计算模型Figure 6 Calculation model when single hollow thin-walled section were used for the main piers

图7 主墩为双空心薄壁墩时计算模型Figure 7 Calculation model when double hollow thin-walled section were used for the main piers

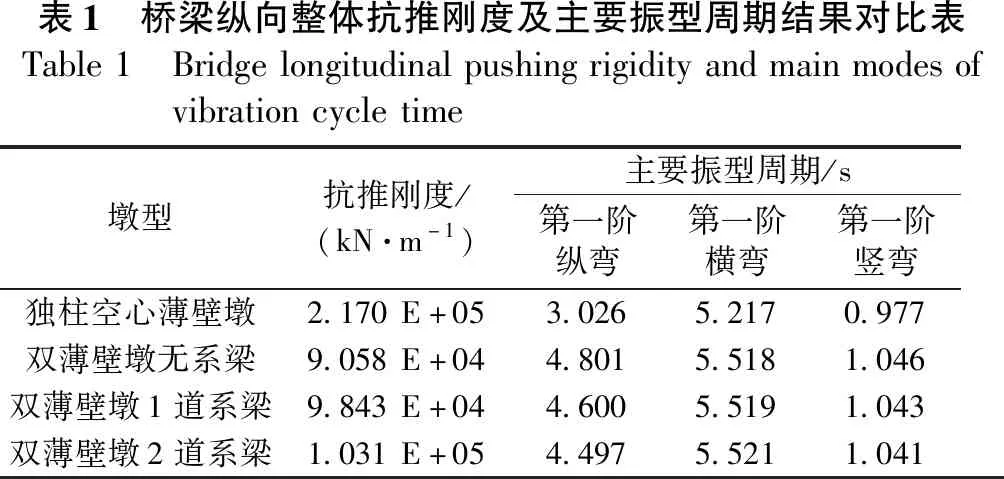
表1 桥梁纵向整体抗推刚度及主要振型周期结果对比表Table1 Bridgelongitudinalpushingrigidityandmainmodesofvibrationcycletime墩型抗推刚度/(kN·m-1)主要振型周期/s第一阶纵弯第一阶横弯第一阶竖弯独柱空心薄壁墩2.170E+053.0265.2170.977双薄壁墩无系梁9.058E+044.8015.5181.046双薄壁墩1道系梁9.843E+044.6005.5191.043双薄壁墩2道系梁1.031E+054.4975.5211.041

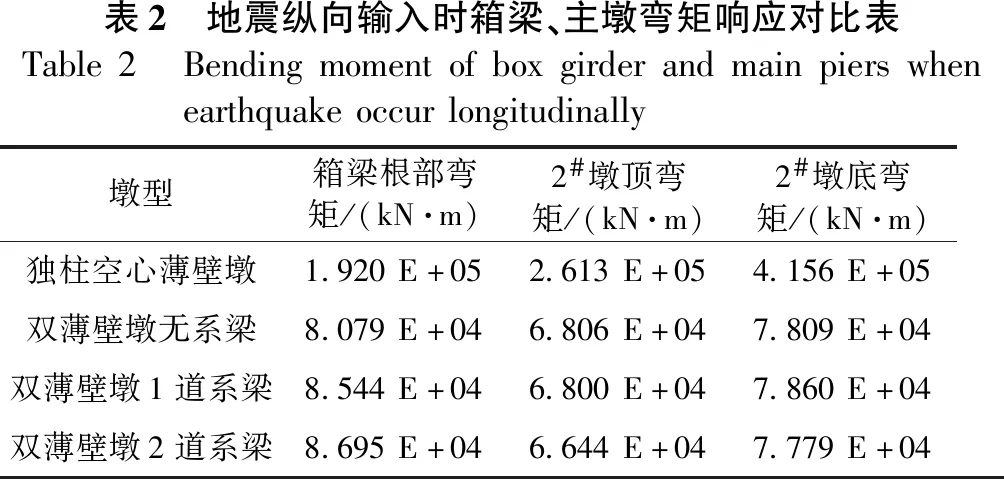
表2 地震纵向输入时箱梁、主墩弯矩响应对比表Table2 Bendingmomentofboxgirderandmainpierswhenearthquakeoccurlongitudinally墩型箱梁根部弯矩/(kN·m)2#墩顶弯矩/(kN·m)2#墩底弯矩/(kN·m)独柱空心薄壁墩1.920E+052.613E+054.156E+05双薄壁墩无系梁8.079E+046.806E+047.809E+04双薄壁墩1道系梁8.544E+046.800E+047.860E+04双薄壁墩2道系梁8.695E+046.644E+047.779E+04

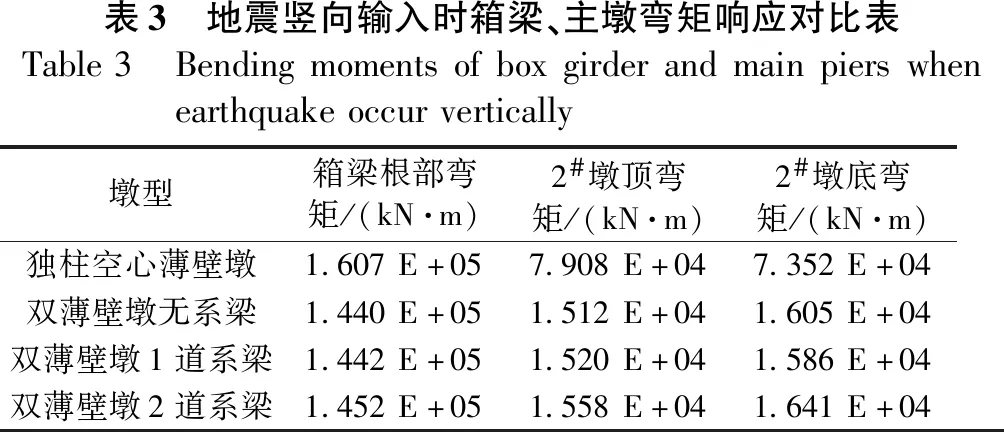
表3 地震竖向输入时箱梁、主墩弯矩响应对比表Table3 Bendingmomentsofboxgirderandmainpierswhenearthquakeoccurvertically墩型箱梁根部弯矩/(kN·m)2#墩顶弯矩/(kN·m)2#墩底弯矩/(kN·m)独柱空心薄壁墩1.607E+057.908E+047.352E+04双薄壁墩无系梁1.440E+051.512E+041.605E+04双薄壁墩1道系梁1.442E+051.520E+041.586E+04双薄壁墩2道系梁1.452E+051.558E+041.641E+04

从表1看出，2#、3#桥墩采用双薄壁墩时，全桥抗推刚度比采用独柱式空心薄壁墩时减小约50%，第一阶纵弯振型的周期显著延长，横弯与竖弯振型周期稍微延长，差异不大。双薄壁墩中间是否设置横系梁对抗推刚度及振型周期影响甚微。

从表2看出，2#、3#桥墩采用双薄壁墩时，与采用独柱式空心薄壁墩时相比，箱梁根部弯矩、2#墩顶弯矩、2#墩底弯矩均大幅降低(双薄壁墩时，表中数据为单墩柱受力)。

从表3看出，2#、3#桥墩采用双薄壁墩时，与采用独柱式空心薄壁墩时相比，箱梁根部弯矩降低约10%、2#墩顶弯矩、2#墩底弯矩均大幅降低(双薄壁墩时，表中数据为单墩柱受力)。

综合以上分析结果，主墩采用双薄壁墩有利于箱梁抗震，且桥墩的地震力也大幅降低。双薄壁墩中间是否设置横系梁对桥梁抗震性能影响较小，考虑施工稳定性，根据桥墩高度可以设置1～2道横系梁，该实例工程2#、3#桥墩高度达100 m以上，设置2道横系梁。

3 箱梁抗震分析

该实例工程跨径大于150 m，根据JTG/T B02-01-2008《公路桥梁抗震设计细则》为A类桥梁，需要进行E2地震作用下的抗震计算。本项目E2地震取50 a超越概率2%，地震动峰值加速度为0.202g，特征周期为0.45 s。进行E2地震时程分析时，采用3组人工合成波，计算结果取最大值。成桥运营阶段恒载及E2地震作用下箱梁根部截面内力情况见表4。

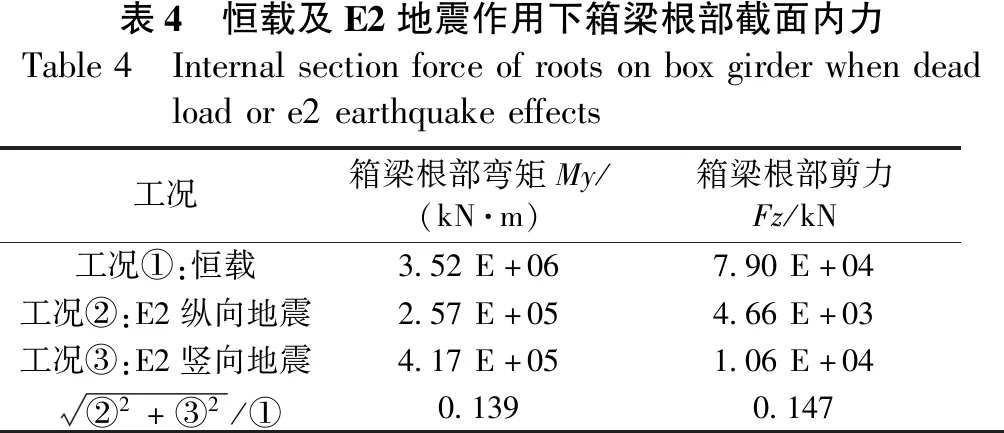
表4 恒载及E2地震作用下箱梁根部截面内力Table4 Internalsectionforceofrootsonboxgirderwhendeadloadore2earthquakeeffects工况箱梁根部弯矩My/(kN·m)箱梁根部剪力Fz/kN工况①:恒载3.52E+067.90E+04工况②:E2纵向地震2.57E+054.66E+03工况③:E2竖向地震4.17E+051.06E+04②2+③2/①0.1390.147

从表4可看出，E2地震纵向与竖向同时作用时，箱梁根部弯矩为恒载时的13.9%；箱梁根部剪力为恒载时的14.7%；且竖向地震作用的贡献较大。

连续刚构桥横桥向的荷载主要为风荷载。风荷载及E2横向地震作用下箱梁根部及跨中的横桥向弯矩Mz对比情况见表5。

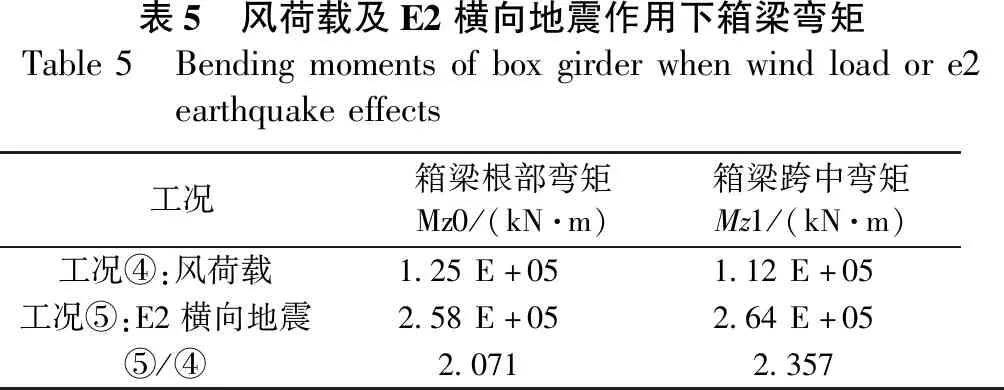
表5 风荷载及E2横向地震作用下箱梁弯矩Table5 Bendingmomentsofboxgirderwhenwindloadore2earthquakeeffects工况箱梁根部弯矩Mz0/(kN·m)箱梁跨中弯矩Mz1/(kN·m)工况④:风荷载1.25E+051.12E+05工况⑤:E2横向地震2.58E+052.64E+05⑤/④2.0712.357

从表5可看出，E2横向地震作用下箱梁根部及跨中弯矩远大于风荷载的效应，对箱梁横向验算起控制作用；且箱梁跨中弯矩大于根部弯矩，由于跨中截面的梁高小，对设计不利。

值得说明的是，该实例工程的抗震设防烈度为7度，地震动峰值加速度为0.10g，若桥梁位于8度或更高烈度地震区，箱梁的地震响应会相应成倍增大，因此高烈度地震区连续刚构桥箱梁设计时应考虑地震作用。

4 减震措施研究

大跨径连续刚构桥梁的常规设计中，上部结构一般采用预应力混凝土箱梁结构，与主墩固结，与辅助墩、交界墩或桥台处采用支座连接。当箱梁、主墩的结构尺寸确定后，若需要提高箱梁的抗震性能，减小其地震响应，可采取的减震措施有限，其原因有：①连续刚构桥纵桥向和横桥向刚度主要受主墩控制；刚度减小余地有限;②连续刚构桥箱梁端部竖向振动幅度极小，支座几乎无竖向变形耗能条件；③箱梁和主墩在地震作用下一般要求保持弹性，对变形控制严格。为了研究在不中断交通的情况下，提高大跨径连续刚构桥梁的抗震性能，减小箱梁在地震作用下的效应，同时不增加主墩的地震响应，仍以前述工程为例，提出2种减震方案：①在辅助墩和桥台处设置高阻尼隔震橡胶支座，每处横桥向各2个；②在方案一的基础上，在两岸桥台与箱梁之间沿纵桥向各设置2个粘滞阻尼器。

高阻尼隔震橡胶支座在常规桥梁中具有良好的减震效果[12]，可以采用双线性恢复力模型来模拟[13]，见图8。各支座的初始刚度K1、屈服后刚度K2，屈服力Fy见表6。

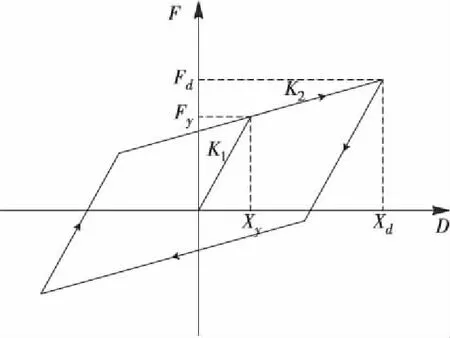
图8 高阻尼隔震橡胶支座的恢复力模型Figure 8 Restoring force model of high damping seismic isolation rubber bearing

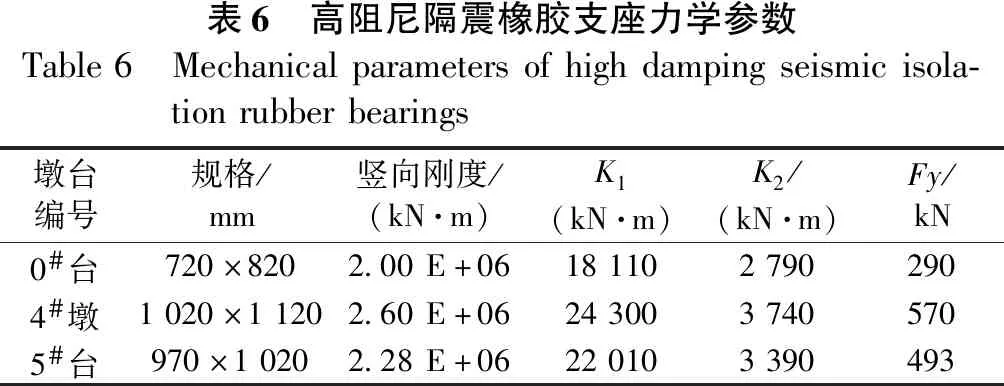
表6 高阻尼隔震橡胶支座力学参数Table6 Mechanicalparametersofhighdampingseismicisola-tionrubberbearings墩台编号规格/mm竖向刚度/(kN·m)K1(kN·m)K2/(kN·m)Fy/kN0#台720×8202.00E+061811027902904#墩1020×11202.60E+062430037405705#台970×10202.28E+06220103390493

粘滞阻尼器为速度相关型，在近断层地震作用下的减震效果显著[14]，构造示意见图9，其力学公式为：

Fd=C·Vα

式中:Fd为阻尼力；C为阻尼系数；V为相对速度；α为速度指数。本项目C=2 000 kN/(m/s)α，α=0.30。

图9 粘滞阻尼器构造示意图Figure 9 Structure schematic diagram of viscous damper

在本工程原设计中，辅助墩和桥台处设置盆式橡胶支座。为比较原设计与减震方案①和②时箱梁和桥墩的地震响应，采用3组人工合成波进行E2地震非线性时程分析，计算结果取最大值。非线性时程分析采用常加速度直接积分法，阻尼矩阵采用瑞利阻尼，E2纵向地震主要计算结果见表7。

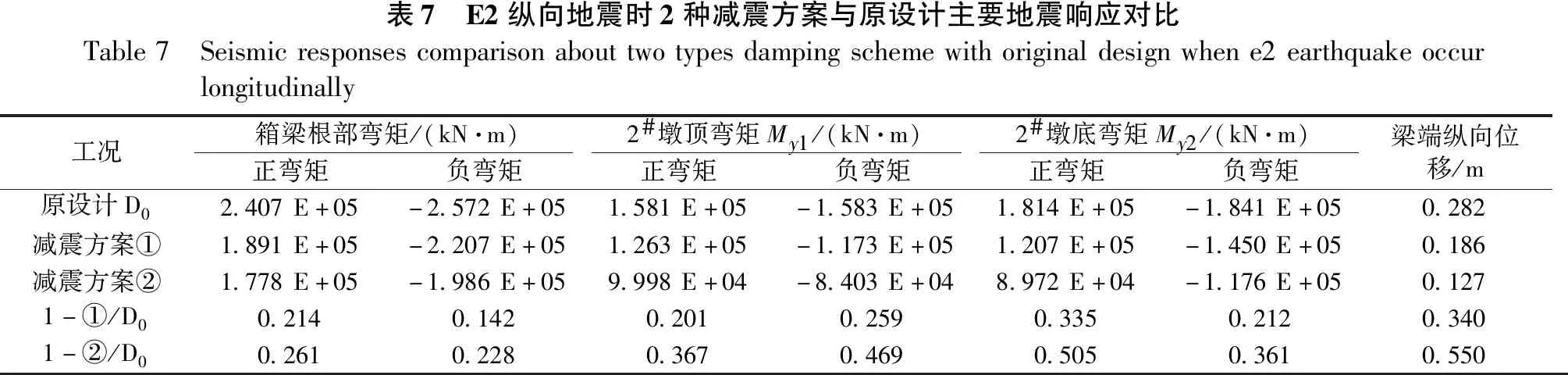
表7 E2纵向地震时2种减震方案与原设计主要地震响应对比Table7 Seismicresponsescomparisonabouttwotypesdampingschemewithoriginaldesignwhene2earthquakeoccurlongitudinally工况箱梁根部弯矩/(kN·m)2#墩顶弯矩My1/(kN·m)2#墩底弯矩My2/(kN·m)正弯矩负弯矩正弯矩负弯矩正弯矩负弯矩梁端纵向位移/m原设计D02.407E+05-2.572E+051.581E+05-1.583E+051.814E+05-1.841E+050.282减震方案①1.891E+05-2.207E+051.263E+05-1.173E+051.207E+05-1.450E+050.186减震方案②1.778E+05-1.986E+059.998E+04-8.403E+048.972E+04-1.176E+050.1271-①/D00.2140.1420.2010.2590.3350.2120.3401-②/D00.2610.2280.3670.4690.5050.3610.550

从表7得出，减震方案①与原设计相比，箱梁根部弯矩最大减小21.4%；主墩顶弯矩最大减小25.9%，主墩底弯矩最大减小33.5%，梁端纵向位移减小34.0%，减震效果显著。减震方案②的减震效果进一步提高，与原设计相比，箱梁根部弯矩最大减小26.1%；主墩顶弯矩最大减小46.9%，主墩底弯矩最大减小50.5%，梁端纵向位移减小55.0%。

在横向地震作用下，纵向粘滞阻尼器不发挥作用，高阻尼隔震橡胶支座可发生剪切变形而耗能。E2横向地震主要计算结果见表8。

从表8得出，在辅助墩和桥台处设置高阻尼隔

表8 E2横向地震时减震方案①与原设计主要地震响应对比Table8 Mainseismicresponsescomparisonaboutno.1dampingschemewithoriginaldesignwhene2earthquakeoccurtransversely工况箱梁跨中弯矩/(kN·m)2#墩顶弯矩My1/(kN·m)2#墩底弯矩My2/(kN·m)正弯矩负弯矩正弯矩负弯矩正弯矩负弯矩原设计D02.64E+05-2.66E+055.676E+04-4.892E+043.512E+05-3.910E+05减震方案①1.907E+05-1.908E+054.034E+04-4.440E+043.589E+05-3.374E+051-①/D00.2790.2840.2890.092-0.0220.137

震橡胶支座对箱梁和主墩横桥向抗震有利，其中跨中弯矩最大可减少28.4%，主墩顶弯矩最大可减小28.9%，主墩底弯矩最大可减小13.7%。

综合纵桥向与横桥向减震效果来看，在辅助墩和桥台处设置高阻尼隔震橡胶支座，并在两岸桥台与箱梁之间沿纵桥向设置粘滞阻尼器是一种效果显著的组合减震措施，可以大幅度降低箱梁和主墩的地震响应。

大跨度连续刚构桥的箱梁受恒载、活载、梯度温差、体系温度、收缩徐变等因素影响，容易出现开裂现象[15]，当需要提高其抗震性能时，可以将原设计的盆式橡胶支座更换为尺寸相当的高阻尼隔震橡胶支座，同时在桥台或交界墩与箱梁之间设置纵桥向粘滞阻尼器，这种组合减震措施不需要中断交通。