基于因子分析法的某流域城市经济发展竞争力研究
2020-05-15李燃,廖亮
李 燃,廖 亮
(安徽建筑大学 经济与管理学院,安徽 合肥 230601)
20世纪80年代以前,学术界对流域城市的研究多集中在水利开发和水土保持,直到1984年,张思平构造出流域经济学的理念,力图把经济学与流域地理概念利用相结合,填补了这一学科领域的空白。后来逐步有学者开始研究流域经济发展,顾卫平(1992)探究了流域城市经济开发现状及在我国经济发展战略中的地位[1]。李炬(1995)分析了流域城市的有利条件和制约因素,提出了流域城市经济发展规划的组成部分、产业结构转型和要素重组[2]。本世纪初,覃成林教授在流域城市经济空间分异领域成果颇丰[3-5],引起了一阵流域城市经济研究的热潮。目前,区域经济的研究正是经济学研究从平面到空间发展的大趋势之一,研究流域城市经济发展状况有利于增强流域经济发展竞争力,促进流域城市建设,增加人民幸福感。
1 城市经济发展竞争力评价体系
1.1 城市发展竞争力研究现状与指标选择
目前,学术界对城市发展竞争力并未有明确的定义。国内学者倪鹏飞表示城市发展竞争力是指某个城市在扩张和成长阶段中和其他城市做对比所特有的吸收、争夺、获取、控制和转化资源,占领和控制经济市场,以创造价值,为民众创造利益的能力[6]。闫二旺通过倪鹏飞构建的城市竞争力指数,对流域城市5个省会城市和15项竞争力指数进行数据剖析,并展示了以省会城市为核心建立城市群的思路[7]。李杰也选择因子分析法对东部地区五个省会城市进行竞争力数据运算和对比,同时对发展城市竞争力提出了新的意见[8]。王恩泽等采用主成分分析法确定中原城市竞争力,表明了中原城市群竞争力提升的发展轨迹[9]。
笔者认为城市竞争力评价指标众多,本文主要研究城市经济发展竞争力,如果一个城市的经济快速良好地发展,势必会带来人民生活、教育质量、交通状况、科学技术等方面的提升。李敏纳曾在其文章中选取流域城市73个地区作为研究对象,为保证数据、统计方法的一致性,本文选取《中国城市统计年鉴2018》上的若干个城市作为样本,根据肖庆业提出的城市竞争力评价指标体系构建的科学性、定量性、全面性、易实现性等原则[10],选取的经济发展竞争力评价指标有:年末单位在岗人员数/人、地区生产总值/万元、人均GRP/元、服务业占GRP的比重/%、固定资产投资(不含农户)/万元、房地产开发投资/万元、外企和港澳台企业产值/万元、国家财政收入/万元、年末金融服务业各项存款余额/万元、年末金融服务业各项贷款余额/万元、当年实际吸收外资金额/万元、在岗职工平均工资/元、社会消费品零售总额/万元、医疗卫生机构数/个、每万人高等学校在校生人数/人等15个指标,且指标与经济发展均具有正相关性。
1.2 模型构建
因子分析法来自英国科技工作者查尔斯在十九世纪初发表的学术论文。本文采用的是R型因子分析,利用变量做因子分析,旨在变量较多、原始数据样本信息较好的情况下,组成新的因子,计算各城市的因子得分,将最终数据得分进行排列顺序。因子分析的数学模型为:
(1)
简写为:X=CT+cφ。其中X= (X1,X2…Xm) 为可测量的m个指标所构成的m维随机向量,T=(T1T2…Tm) 是不可测的向量,T叫做X的公共因子,cij是因子载荷在第i个变量、在第j个公共因子上的负荷。矩阵C是因子载荷矩阵,φ为X的特殊因子。一般要求ε的协方差矩阵是对角矩阵,φ表示统计误差[11]。
2 数据处理
通过软件对所选取的指标进行分析。KMO和巴特利特检验如表1所示,显示结果KMO值为0.773,符合因子分析标准。球形检验P值<0.05,说明所提取的各个参数变量之间具有比较强的关联。

表1 KMO和巴特利特检验
因子分析的重点之一就是将所得到的抽象因子的具体含义进行合理说明,然而仅仅通过特征根、特征向量获得的因子载荷矩阵很难表示出公共因子的内涵。于是就必须采用因子旋转的方式,使每个参数变量在同一个因子上有载荷[12]。本文采用的方法为最大方差法,提取出特征值为>1的因子,第一个因子的方差占所有因子方差的63.711%,第二个因子占比为11.908%,第三个因子占比为9.524%,旋转后的前三个因子累计贡献率达85.143%,因此,前三个因子可以很好地用来描述城市的经济发展。
成分得分系数矩阵如表2所示,从表中可以得到3个因子的得分公式为:
F1=0.116X1+0.162X2+0.041X3-0.192X4+0.195X5+0.088X6+0.190X7+0.146X8
+0.035X9+0.005X10+0.160X11-0.079X12+0.106X13+0.050X14-0.109X15
F2=0.022X1-0.118X2-0.120X3+0.472X4-0.161X5+0.070X6-0.173X7-0.076X8
+0.160X9+0.200X10-0.102X11+0.155X12+0.024X13+0.026X14+0.368X15
F3=-0.114X1+0.098X2+0.501X3-0.023X4+0.003X5-0.101X6+0.001X7+0.073X8
-0.055X9-0.010X10-0.024X11+0.379X12-0.054X13-0.359X14-0.021X15

表2 成分得分系数矩阵
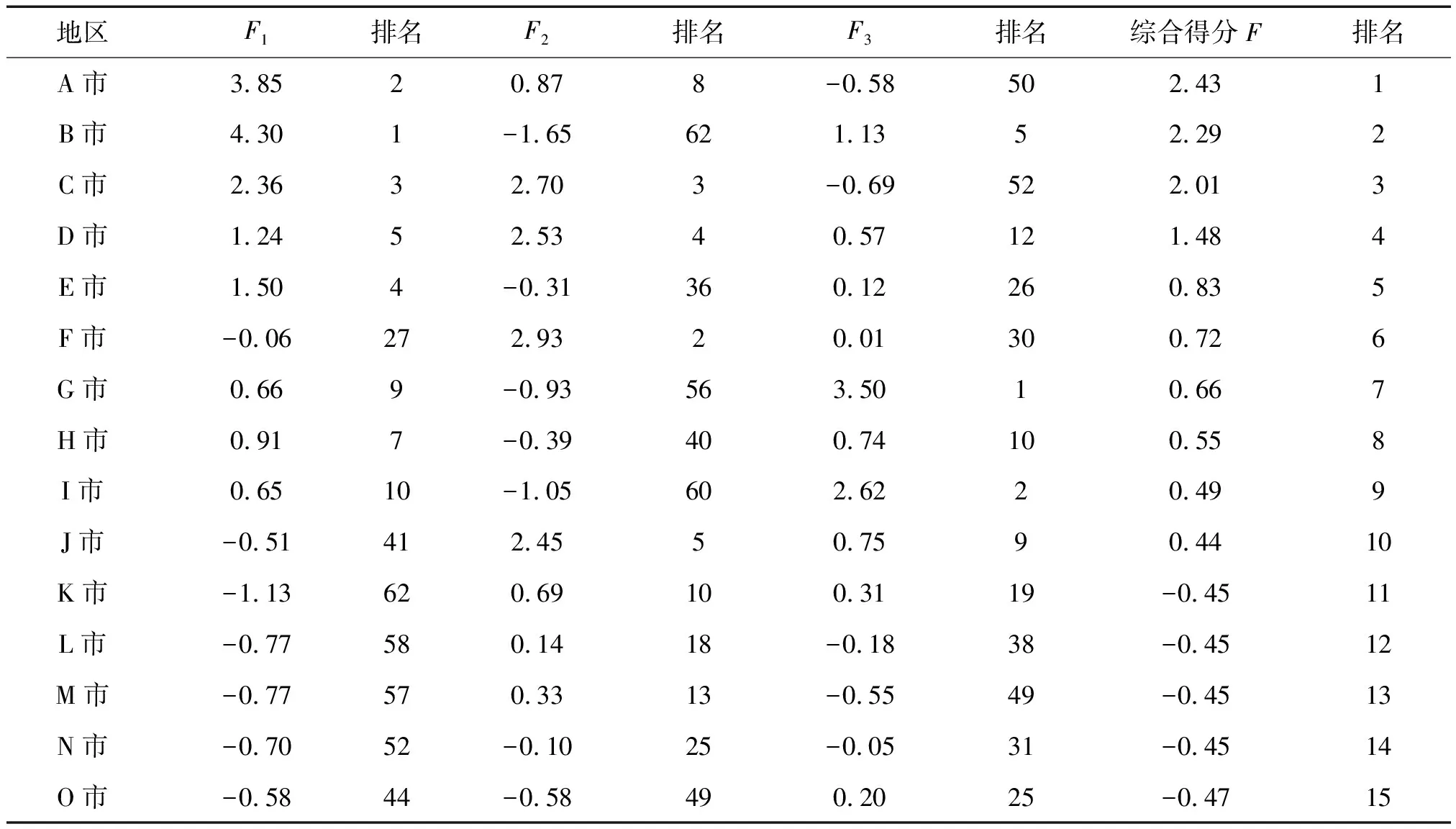
表3 因子得分与综合得分情况
表达式中F1、F2、F3分别表示三个因子的分数,X1-X15分别表示年末单位在岗人员数到每万人高等学校在校生人数15个变量标准化处理之后的数值。为了进一步比较,还需要将三个公因子以每个因子的方差收益率占累计收益率(分别用λ1、λ2、λ3表示)的比重作为权重来加权来计算综合分数(用F表示),综合得分公式如下:
(2)
通过电子表格软件运算出各城市的因子分数和综合分数,顺序情况如表3所示,可以看出通过因子分析的综合分数情况与实际的城市经济发展情况是吻合的。
3 结 语
综合得分处于前五位的依次是:A市、B市、C市、D市、E市,处于最后五位的依次是K市、L市、M市、N市、O市,除了N市,其他城市均不在流域沿岸,距离流域较远。因子分析的结果表明流域城市经济发展不平衡不充分,差异化显著,这是亟待解决的问题。
