进气型式对压入式矿用对旋主通风机内部流动及性能的影响
2020-05-14陈庆光邹璐瑶孙鲁杰DulminaWijerama
陈庆光,邹璐瑶,李 哲,孙鲁杰,Dulmina Wijerama
(山东科技大学 机械电子工程学院,山东 青岛 266590)
对旋风机因其结构紧凑、安装使用方便,以及效率高、风量大和反风性能好等方面的优点,近20年来在我国矿井通风、地铁隧道换气和锅炉引风等工程领域得到了广泛应用[1,2]。而不稳定进气条件(如进口段安装90°弯管、消声器等附加结构)对风机内部流场及风机叶片工作的稳定性都具有不可忽视的影响,直接影响到煤矿井下人员、通风机设备和生产的安全性。
针对不同来流条件下的风机/压气机内部流场的分析,国内外相关学者已进行了大量的研究。Kennedy等[3]以通用电气CF34-3A发动机为研究对象,采用SST k-ω湍流模型揭示了不同来流角度下转子进口流场的流动分离特征,并通过试验数据分析验证了数值模拟结果的可靠性;Arshad等[4]通过改变一单级低速压气机叶轮入口的径向形变来模拟压气机的动态失速特性,并结合试验得出,进口变形所引起的叶片载荷的变化是定义失速先兆是模态波型或突尖型的前提;Page等[5]对四种进气畸变型式的跨音速风机进行转子失速特性的研究,结果表明,进气畸变所导致的不稳定的涡流和径向的静压变形分布会对转子性能造成不利影响,但对失速团的状态与发展的影响可以忽略不计。
国内的刘飞等[6]对带有复杂进气箱的大型轴流风机流场进行了数值计算,结果表明,进气箱的复杂性和不合理的轴套结构都会增加叶轮入口处气流流动的不均匀性,并恶化了风机的内部流场。陈庆光等[7]通过对在进口段安装片式消声器的压入式矿用对旋主通风机进气风道内部流场进行数值模拟,发现气流在消声器的出口及下游形成了具有卡门涡街阵列的尾迹,致使风机第一级叶轮的进口流场紊乱,恶化了风机进气条件,并为此提出了消声器的改进方案,有效地改善了风机进气风道内的流动和叶轮的进气条件;张兴发等[8]研究了插板畸变进气条件下压气机内部流场特性及插板畸变对压气机失速起始机制的影响,发现低速压气机稳定边界的波动是由转子进口截面的周向气流流动引起的,插板畸变气流也会影响叶片通道内激波强度和位置。
然而,在矿用主通风机领域,相关研究大都集中在均匀进气条件下通风机内部非定常流场分析方面[9-12],针对由片式消声器与90°弯管组合而成的进气风道所产生的进气畸变流场对通风机内部非定常流动影响的研究,迄今还未见公开报导。
本文以一台以压入式工作的矿用对旋主通风机为研究对象,针对无畸变、弯管畸变和复合畸变3种进气型式,分别建立包括进气道在内的对旋风机全流道几何模型,通过三维非定常流场的数值模拟,对比分析3种进气型式下风机内部的瞬态流场分布,研究畸变进气型式对对旋风机两级叶轮内部流动的影响,为提高以压入式工作的矿用轴流主通风机运行的安全性和稳定性奠定基础。
1 物理问题描述与几何建模
1.1 研究对象
本文选择以压入式工作的FBCDZ-10-No20型矿用对旋主通风机为研究对象,其主要性能参数见表1。

表1 通风机主要结构与性能参数
包括进气风道在内的通风机装置几何结构示意图(Z轴正方向水平向左,X轴正方向垂直纸面向外,Y轴正方向竖直向上)如图1所示,主要包括进气片式消声器、90°矩形截面弯管、过渡段、集流器、第一级叶轮、第二级叶轮和扩散器等部件。本文拟考查以下3种进气型式:图1中去除进口段片式消声器和90°弯管结构为无畸变进气型式;图1只去除进口段片式消声器结构称之为弯管畸变进气型式;图1全部几何结构则称之为复杂畸变进气型式。
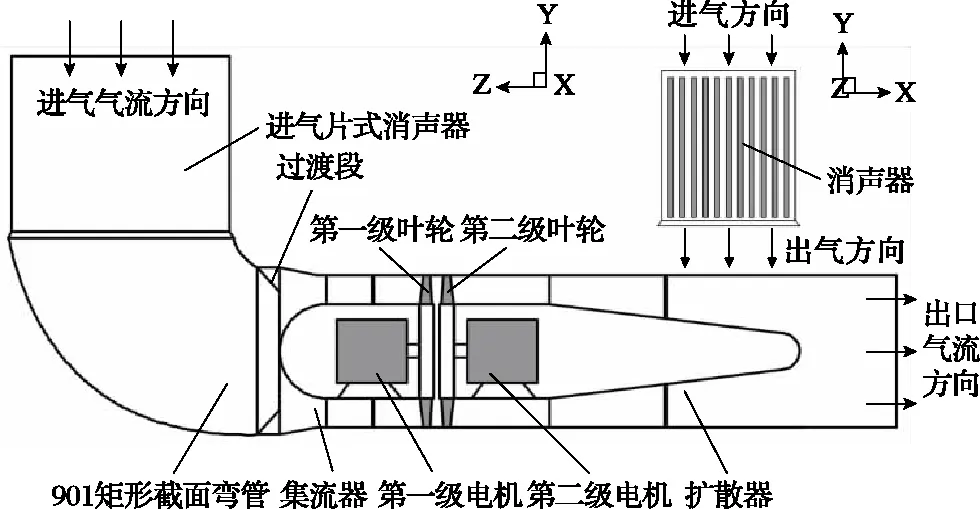
图1 矿用对旋主通风机装置几何结构示意图
1.2 几何建模与网格划分
为了几何建模、网格划分和模拟计算的需要,在不显著影响模拟结果的前提下,对通风机装置几何模型的局部细微结构进行了适当的简化处理,并将整个计算区域划分为6个计算子区域:进气片式消声器、90°矩形截面弯管、集流器入口段、第一级叶轮、第二级叶轮和扩散器,如图2所示。
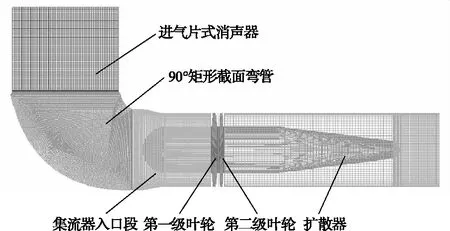
图2 对旋通风机装置全流道网格
考虑到模拟计算的耗时与精度,用六面体单元对对旋风机全流道进行结构化网格划分,动叶区域采用H-O-H型拓扑,其中对两级叶轮叶片的轮毂、前缘(LE)及尾缘(TE)区域进行局部的网格加密,为了满足SST k-ω湍流模型对网格精度的要求,对于叶片表面、轮毂以及机壳壁面,使第一层网格节点到壁面的无量纲距离y+值均小于20,叶轮域网格局部放大如图3所示。
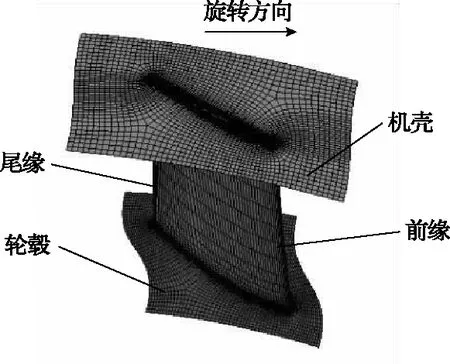
图3 叶轮区域网格
2 数值分析方法与边界条件
针对上述求解域数值求解控制流场的三维非定常Navier-Stokes方程组,引入SSTk-ω两方程模型模拟湍流,与k-ε湍流模型相比,SSTk-ω湍流模型对于边界层边缘流动和自由剪切流采用k-ε湍流模型,而在处理近壁面流动时采用k-ω湍流模型求解,近年来该模型在预测近壁区流动方面的优越性能得到了广泛的认可[3,13-15]。控制方程在时间和空间上的离散分别采用隐式双时间推进法和有限体积法,瞬态求解采用二阶后向欧拉格式。非定常计算的时间步长取为0.0003s,即叶轮转动1.8°所需要的时间,旋转一周需0.06s,每个时间步内最多迭代20次,计算中忽略气流重力的影响。
针对3种进气型式,计算中分别以消声器、90°弯管和集流器的入口截面为计算域的进口边界,扩散器的出口截面为计算域的出口边界,并对扩散器出口段做了适当的延长以减小边界条件对数值模拟结果的影响。计算域入口采用质量流量入口,出口给定相应的压力值,壁面为绝热无滑移壁面条件。进行定常流动模拟时,在计算域中的动-静、动-动交界面处采用冻结转子-静子法(Frozen Rotor Stator)进行数据的耦合传递,而在非定常流动模拟时则采用瞬态转子-静子法(Transient Rotor Stator)。当计算中各项残差小于10-5且计算域进出口流量差都小于10-3时,认为计算收敛。
3 模拟结果与分析
为了降低网格数量对模拟精度的影响,对复杂进气畸变型式下的对旋通风机计算模型进行了网格无关性验证。为了提高网格无关性验证的可靠性,同时考察了全压升和全压效率随网格数的变化情况,如图4所示,当网格数从686万增加到900万时,全压减小了48Pa(约占全压升的1.3%),全压效率增大了0.01%,说明当网格数量大于686万时,风机全压升与全压效率的变化已很不明显。因此,在综合考虑模拟精度和计算时间等因素的情况下,本文最终选取686万网格数进行模拟计算,其中消声器、90°弯管、集流器和扩散器各部件对应区域的网格数分别为21万、56万、32万和100万,两级动叶轮区域的网格数分别为253万和232万。
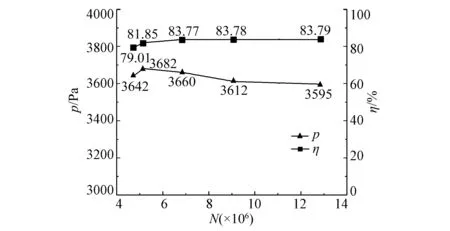
图4 网格无关性验证
3.1 进气风道内流动分析
湍动能可通过湍流强度及平均速度进行估算,是表征湍流脉动剧烈程度的重要指标。第一级叶轮进口上游1.5倍弦长处轴向截面湍动能分布如图5所示。
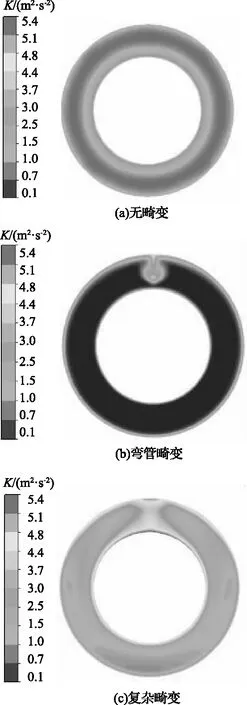
图5 第一级叶轮进口上游1.5倍弦长处轴向截面湍动能分布
从图5可以看出,无畸变进气型式下流场的湍动能具有良好的周向对称性,高湍动能区域主要集中在环形风道内壁面处。而在弯管畸变和复杂畸变进气型式下,环形风道顶部均出现了高湍动能集中区域,并且复杂畸变进气型式下的高湍动能区域范围更大、数值更高,其分布呈“沙漏”状并在近环形风道内外壁面处出现最大值,表明进气风道内的气流流动更加不均匀,其原因就是气流在消声器尾缘产生的卡门涡街阵列再流经90°弯管过程中会进一步产生流动分离和二次流,从而恶化了风机进气风道内的流场[15,16]。可见,较无畸变进气型式,弯管畸变和复杂畸变进气型式下第一级叶轮入口气流的不均匀性显著增加,增强了叶轮入口气流的不稳定性,并极易引起下游叶轮内流动的恶化,这与文献[7]所得结论相一致。
3.2 叶轮内压力脉动特性分析
通过风机叶轮内部流动压力脉动的分析,可以了解流场内部气流的非定常扰动规律。对于无畸变进气型式,如图6所示,在第一级叶轮进口流道靠近叶片前缘的90%径向叶高处,沿周向间隔三个叶片流道分别布置了三个监测点,记为p11、p12、p13;在第二级叶轮进口流道靠近叶片前缘的90%径向叶高处,同样沿周向间隔三个流道分别布置了三个监测点,记为p21、p22、p23。类似地,针对弯管畸变与复杂畸变进气型式,在相同位置布置的监测点分别记为m11、m12、m13,m21、m22、m23与n11、n12、n13,n21、n22、n23。
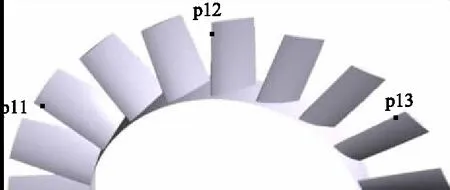
图6 监测点位置布置
对旋风机的叶片通过周期(Blade passing time,BPT)为:
BPT=60/nz
(1)
叶片通过频率(Blade passing frequency,BPF)为:
BPF=nz/60
(2)
式中,n为风机叶轮转速,r/min;z为为叶轮叶片数。
对旋风机前、后两级叶轮的叶片数分别为19和17(见表1),叶片通过频率分别为f1=310.33Hz和f2=277.67Hz。为了分析3种进气型式下风机内部流场的压力脉动特征,将3种进气型式下监测点的静压时域信号进行快速傅里叶变换(FFT),可分别得到其压力脉动频谱,如图7所示。
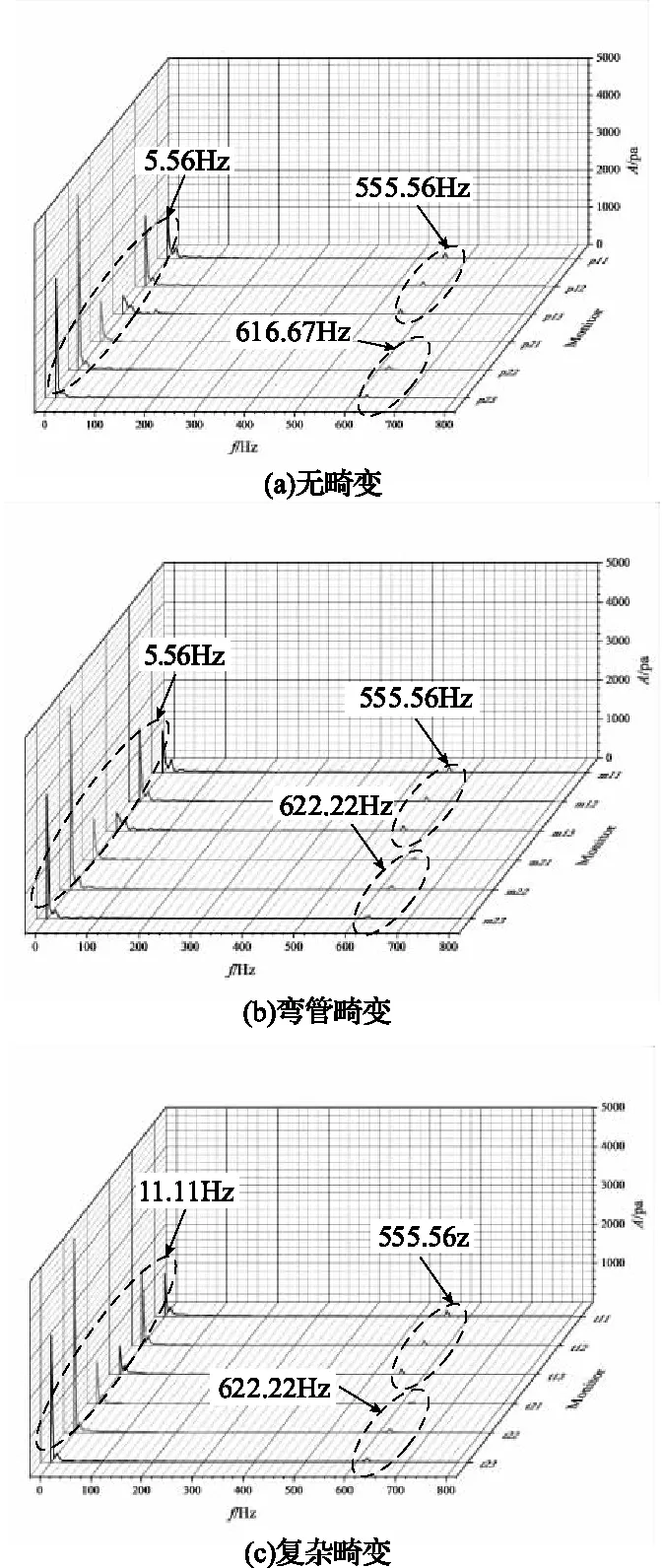
图7 三种畸变进气型式下两级叶轮内部流场的压力脉动频谱
由图7可见,3种畸变进气型式下的叶轮内部流场主要受2%叶片通过频率(BPF)附近低频脉动的影响,这种脉动表现为单个大幅值与多个小幅值脉动的组合;同时还受2倍叶片通过频率(BPF)附近高频脉动的影响,这种脉动表现为单个小幅值脉动。由此可知,无论哪种畸变进气型式,叶轮内部的非定常流场主要受到风机进气风道内不稳定气流所引起的低频、大幅值脉动的影响和不稳定流动与叶片通过频率共同作用的高频、小幅值脉动的影响。从图中还可看到,3种进气型式下压力脉动的最大幅值均出现在第二级叶轮,复杂畸变进气型式下两级叶轮内的压力脉动幅值明显高于其他两种畸变型式,并且两级叶轮内大幅脉动对应的主频及第二级叶轮内小幅脉动对应的次频在数值上皆向后偏移了6Hz,如图7(c)所示。而相对于无畸变型式,弯管畸变型式下的脉动量增幅较小,这说明复杂畸变进气型式下风机进气风道内的不稳定流动所引起的气流脉动对叶轮内部流场的影响不可忽视。
3.3 进气型式对两级叶轮内部流动特性的影响

图8 第二级叶轮Z=1.66m处轴向截面的静压分布
由上文分析可知,在3种畸变进气型式下,第二级叶轮对应监测点的脉动幅值均高于第一级叶轮,故对第二级叶轮流场做进一步分析。第二级叶轮Z=1.66 m处轴向截面的静压分布如图8所示,3种畸变进气型式下的第二级叶轮压力面均出现沿叶高方向的压力梯度,而在叶片吸力面呈现出沿周向分布的压力梯度(第二级叶轮转动方向为顺时针方向),并且高压区皆出现在叶片压力面前缘靠近叶顶处。在叶片吸力面靠近叶片尾缘区域,吸力面表面静压值沿气流方向逐渐升高,出现逆压梯度,说明在叶片吸力面尾缘有可能发生流动分离。
对比图8中3种畸变进气型式下的静压分布云图,还可以看出,图8(c)所示的复杂畸变进气型式下的流场分布很不均匀,叶片压力面的高压区域明显减小,伴随着叶轮的周期性旋转运动,各流道内不稳定的气流流动随着转子周期的增加,会严重影响到第二级叶轮的正常工作。
为进一步考查3种畸变进气型式对风机叶轮域内部流场的影响,3种畸变进气型式下两级叶轮90%叶高处周向截面的速度矢量分布如图9所示。
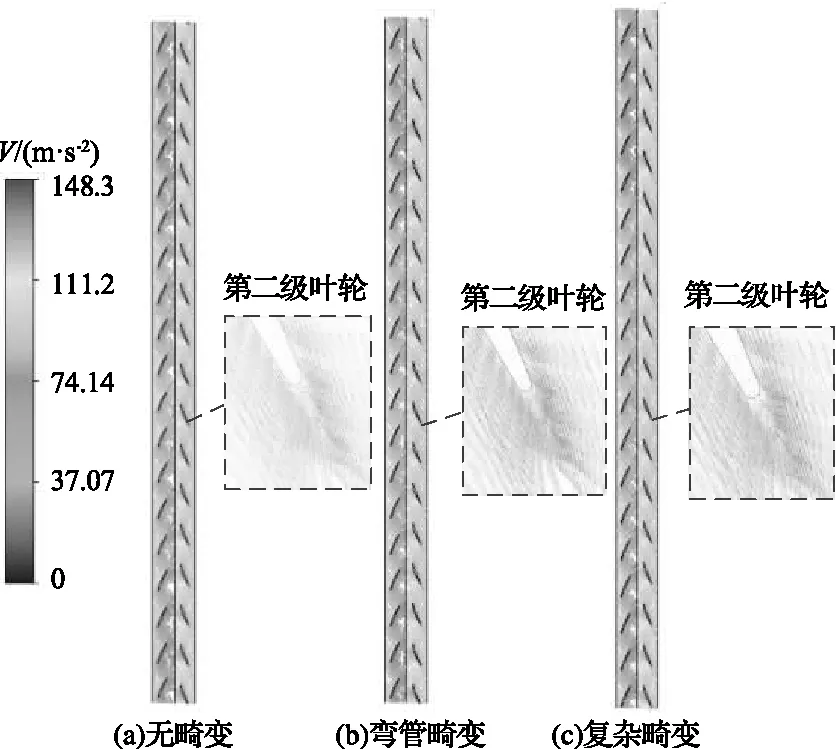
图9 两级叶轮90%叶高处周向截面速度矢量
从图9可以看到,第二级叶轮速度场的整体分布趋势与图8所描述的流场分布近似一致,复杂畸变进气型式下第二级叶轮前缘点速度分布较其他两种型式呈现明显的周向不均匀性。3种畸变进气型式下,第一级叶轮速度场分布相对稳定,第一级叶轮与第二级叶轮均在吸力面靠近前缘处出现高速区且第二级叶轮高速区波动范围更大。从图9中虚线框中所示的第二级叶轮尾缘速度矢量局部放大图可以看出,在第二级叶轮吸力面尾缘处出现了小范围的低速区,图9(c)所示的复杂畸变型式下的尾缘处流场更加紊乱,低速区范围更大。但由于主流速度相对较高,尾缘处的低速区还没来得及发展成为分离涡就被主流带走,只在叶片吸力面的尾缘区域出现了沿气流方向的低速带。
3.4 进气型式对对旋风机性能的影响
3种畸变进气型式下风机全压升与全压效率的数据对比见表2,可以看出,弯管畸变与复杂畸变进气型式下风机全压升与全压效率均出现了不同程度的下降,而复杂畸变进气型式下风机全压升与全压效率值下降更为明显,可见,在风机进风道的进口段安装90°弯管或其与消声器的组合装置对风机性能具有较为显著的影响。
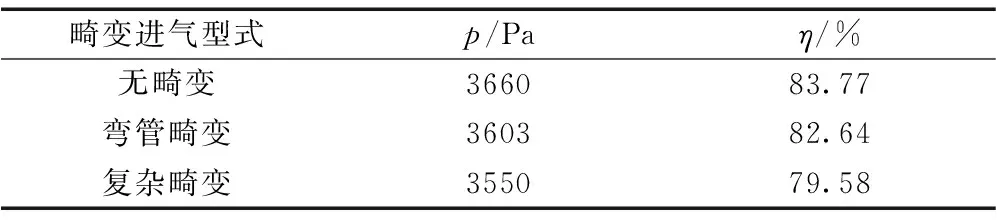
表2 三种进气畸变型式下的风机全压升与全压效率
本文重点分析比较了3种畸变进气型式对对旋风机内部流场及风机性能的影响程度。虽然分析结果已证明无畸变进气型式的影响最小,但实际应用中仍有较多的弯管畸变与复杂畸变进气型式。因此,还需要研究如何采取优化进气弯管结构等措施来改善通风机的进气条件,以达到提高压入式矿用主通风机性能的目的。已在这方面进行了一些有益的探索[7]
4 结 论
本文以压入式工作的矿用对旋主通风机装置为研究对象,分别对3种畸变进气型式下的风机内部三维非定常流场进行数值模拟,以考察畸变进气型式对风机内部流场特性和风机性能的影响,得到以下主要结论:
1)在风机进口段安装90°弯管或安装消声器与90°弯管的组合装置后,第一级叶轮的进口段流场出现了明显的高湍动能区域,流动的不均匀性显著增强。
2)3种畸变进气型式下风机叶轮内部流场在低频段都具有不同幅值的非定常压力脉动,复杂畸变进气型式的脉动幅值最高;无论哪种畸变进气型式,第二级叶轮流场中的脉动量均为最大。
3)从第二级叶轮Z=1.66m处轴向截面的静压和90%叶高处周向截面速度矢量分布图都可看出,弯管畸变和复杂畸变型式下的流场具有明显的周向不对称性;由于第二级叶轮叶片吸力面尾缘处存在逆压梯度,并且尾缘区域出现了沿气流流动方向的低速带,气流在叶片吸力面尾缘有可能发生流动分离。
4)弯管畸变与复杂畸变进气型式下风机的全压升与全压效率皆出现了不同程度的下降,其中复杂畸变进气型式对风机性的能影响最为显著,说明对于风机的设计和运行进气畸变的影响都不可忽视。
