基于场强地图的室内定位技术研究

王韦刚，周 蓉，张云伟，李 韬（南京邮电大学，江苏南京 210023）

0 引言

目前室内定位系统要求既要节约成本［1-3］，又要缩短定位时间。基于指纹库的室内定位技术，能对包括信号指示强度（RSSI）在内的多种测量参数快速地建库［4-6］。其中，采用反演模式的电波传播模型，能迅速构造用于定位的场强地图，通过指纹库匹配的方式进行定位，该技术近年来颇受关注。估计值和收敛准则对计算结果有较大影响，此方法求得的解仍然存在较大的误差。利用反演模式下的电波传播模型，构造场强地图进行快速定位是当前比较实用的方法之一。Y.Shu 等人［7］采用共轭梯度法（CGM——Conjugate Gradient Method）定位室内中的位置，但是由于共轭梯度法的局限性，该方法只能在特定的环境下使用。M.Leigsnering 等人［8］采用正交匹配追踪法（OMP——Orthogonal Matching Pursuit）求解病态方程组，有效地减小了计算误差，但是该方法的不足之处是计算复杂度比较高。S.Liu 等人［9］利用改进的正交匹配追踪法求解病态方程组，由于初始在线匹配定位时，多种匹配方法也已经运用到相关定位算法中。X.Liu 等人［10］利用并行最近邻匹配（KNN——K Nearest Neighbor）搜索算法对空间细分并过滤，该方法有助于减少内存占用，其不足之处是精度较低。H.Feng等人［11］提出了一种用KNN 算法对旁路图像进行熵估计的方案，该方法能有效地对互信息进行评估。X.Wang 等人［12］设计了一种基于机器学习中KNN 匹配的分类器，该分类器的安全较高，性能较好，但不适用于数据多的情况。P.Botsinis 等人［13］提出一个INTRI 室内定位框架，该框架运用了加权最近邻匹配（WKNN——Weight K Nearest Neighbor）算法进行位置匹配，但其可实施性较差。

1 离线阶段

1.1 基于电磁传播模型的构建

在无线信号传播过程中，会存在各种物体遮挡传输，大量的信号为非视距（NLOS）传播，只有极少量信号是视距（LOS）传播［14］。室内的无线传输存在多径效应，使得接收信号强度实时变化较大，也都会影响定位效果。然而，场强的波动依然在一定范围内，只要统计样本足够则可消除小尺度衰落的影响［15］，通过中值滤波可获得测试点的有效场强。

为了简化问题，将预测区域分成网格，图1是信号经过虚拟路径到达接收机的场景图。图1 中AP 是发射机的位置表示第i（i=1⋅⋅⋅M）条射线，Ai是第i条射线进入预测区域的交点，Bi是到达接收机的点，Gj表示第j（j=1⋅⋅⋅N）个网格。

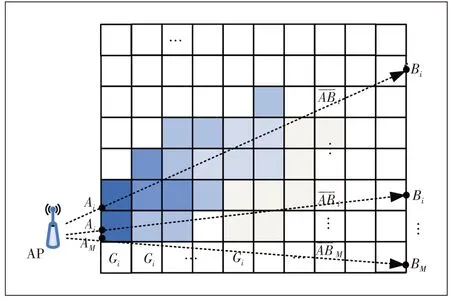
图1 无线传播模型示意图

图1 中用αj表示每个网格对应信号的衰减因子，di,j表示传播路径i经过第j个网格的距离，如果虚拟传播路径不经过某个网格，则该网格对应的距离为0。

设接收端与发射源之间的传播损耗表示为：

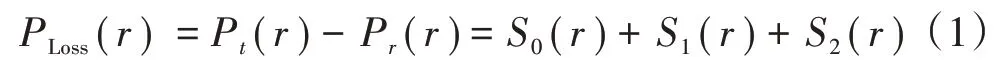
式中：

PLoss(r)——信号强度衰减

Pt(r)——信号的发射功率

Pr(r)——接收信号功率

S0(r)——空间传播时由距离引起的衰落

S1(r)和S2(r)——为阴影衰落和小尺度衰落

由于信号强度的衰减随距离空间变化，因此可以定义信号强度衰减因子α(r)为：

式中：

r——传播距离

衰减因子表示单位传播距离上的强度衰减量。式（2）也可改写为积分的形式，定义积分算子α(r)，可以将转化为：

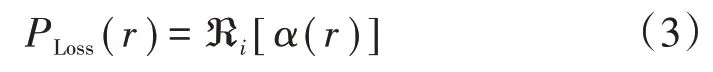
它表示通过对积分算子ℜi的积分，信号强度的损耗表现为通过传播路径时所经历的总衰减。

当信号沿传播路径穿过网格时，每个网格有不同的衰减因子，用αj表示区域内不同网格的衰减因子。当不通过某个网格时，则该网格的衰减因子为零。假设用i表示虚拟传播路径，则每条路径的损耗为：

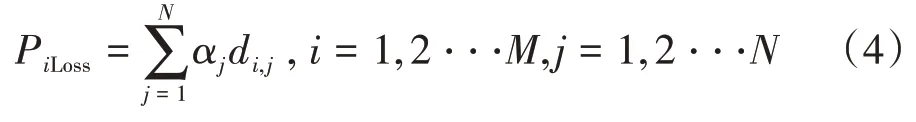
全部M条路径组成的总损耗为：

式中：

PLoss——信号在预测区域内的信号强度损耗，且PLoss=[P1Loss,P2Loss,⋅⋅⋅,PMLoss]

D——由信号经过预测区域内每个网格的距离组成的M×N矩阵，记作

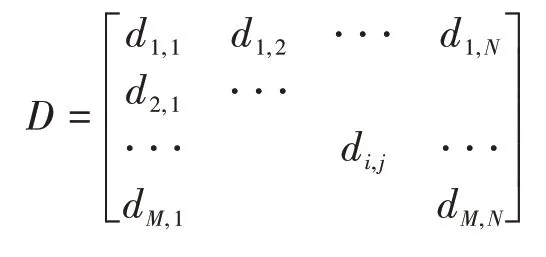
α——衰减因子向量，且α=α1，α2，⋅⋅⋅，αj，⋅⋅⋅，αN

E——由级数展开时的数据估计的近似性和测量引起的误差

1.2 新型反演模式的信号模型的求解

式（5）是一个病态方程组，它有多种求解方法。传统的方法有代数重建法（ART——Algebraic Reconstruction Technique）［16］、雅可比（Jacobi）算法［17］、共轭梯度法（CGM）、正交匹配追踪（OMP）等［9］。为了提高网格中衰减因子的求解准确度，本文提出使用追踪共轭梯度法（PCG——Pursuit Conjugate Gradient）求解网格中的衰减因子。

根据压缩感知的知识，高维的稀疏信号可以从低维的非相关观测值进行重构。在式（5）中，需要从M维观测值PLoss恢复N维信号α，其中M≪N。然而α本身不具有稀疏性，需要找到某个稀疏基ψ，并有α=ψθ，稀疏矩阵ψ为N×N维，系数θ为N×1 维的列向量且是K稀疏的（K≪N）。

设b=PLoss-E，则式（5）可写为：

设Η=Dψ，则相当于求解：

由于展开的系数θ具备稀疏性，则可由压缩感知技术中的OMP 方法恢复稀疏矩阵θ，进而由α=ψθ可得到衰减因子α。求解过程如下：

先初始化参数设置，令r0=b，Λk=φ，k=1，寻找λk，使得：

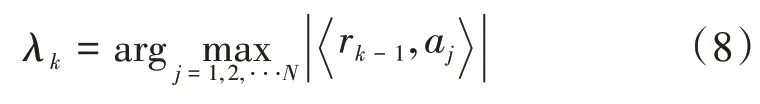
式中：

rk——残差

k——迭代次数

Λk——k次迭代索引（列序号）的集合

λk——第k次迭代找到的索引号

aj——矩阵Η的第j列

Ηk——按索引Λk选出的矩阵Η的列集合

θk——θ中提取的k×1的列向量

令Λk=Λk-1⋃λk，Ηk=Ηk-1⋃aj，在此情况下，系数方程b=Ηkθk求解公式为：

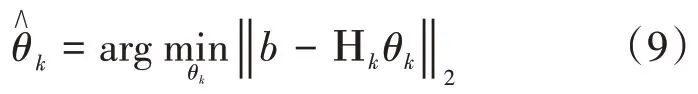
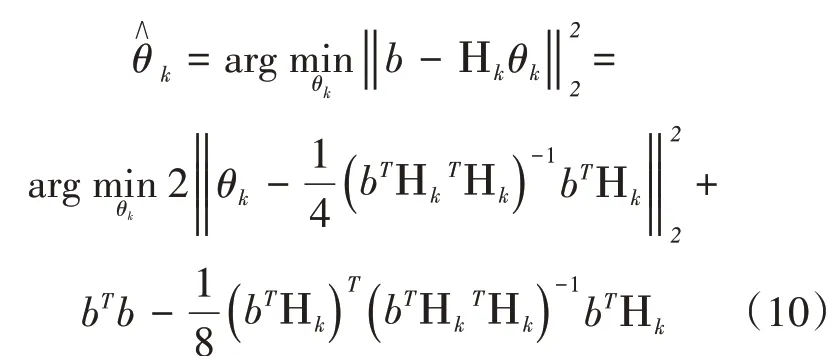
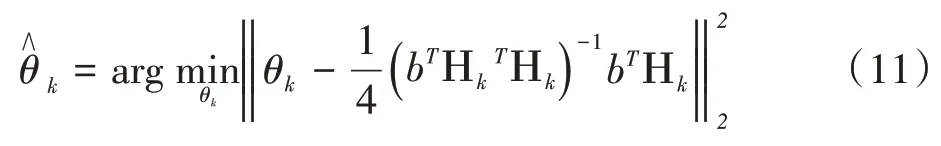
进一步，式（11）可以用共轭梯度法求解。设t是共轭梯度法中的迭代次数，初始值为θ0，初始梯度方向为其 中=[1,...,1]T，k×1维，g0表示初始值为θ0时的一阶偏导数，建立新的目标函数为：

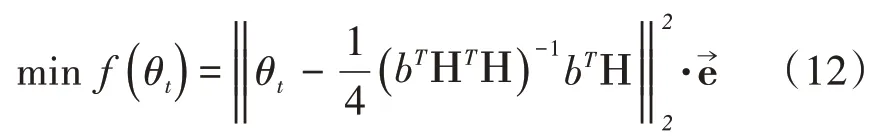
共轭梯度法迭代式为：

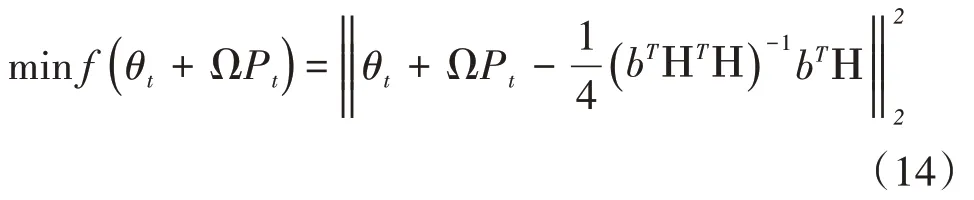
可求得Ω，进而可求式（14）的一阶偏导数gt，表示式为：

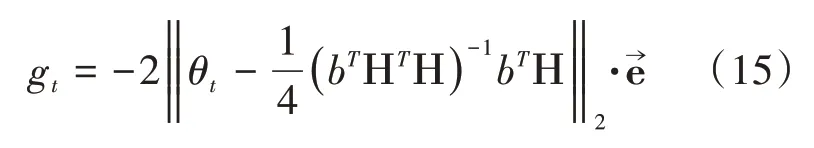
如果‖gt‖＞ε，则根据FR（Fletcher-Reeves）公式，得到下降方向：

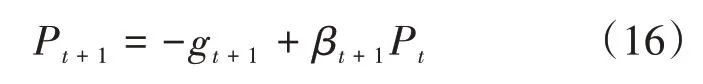
将式（16）代入式（13），依次迭代直至‖gt‖＜ε，得到θt。

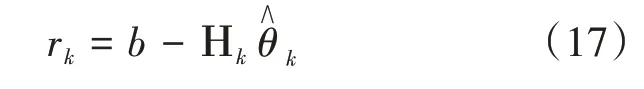
如果k≤K，令k=k+1，继续寻找索引λk；否则重构出，进而求出α。

PCG算法步骤如表1所示。

表1 PCG算法

为了对各种算法复杂度进行分析，各算法迭代次数总体分析如表2 所示。k表示索引的迭代次数，t是共轭梯度法迭代次数。

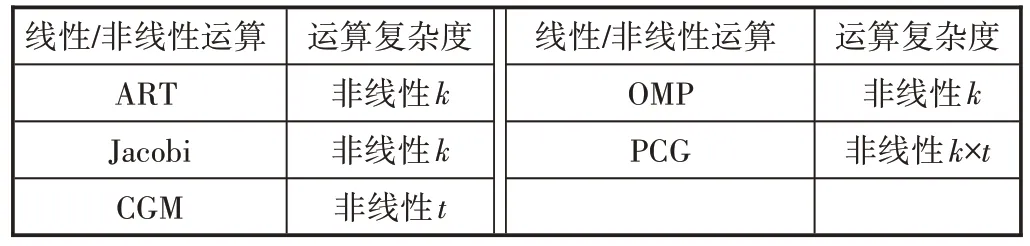
表2 几种方法的典型性能分析比较

PCG 算法的迭最大代次数由稀疏度K和迭代次数t2 项决定，前者在稀疏的前提条件下是小于M的常数，而后者则已经由经典的OMP 算法证明是收敛的［9］。

1.3 场强地图的建立

通过对预测区域网格作精细划分，并利用衰减因子对各位置的场强统计特征值做出预测，得出网格的信号场强的计算方法如下：

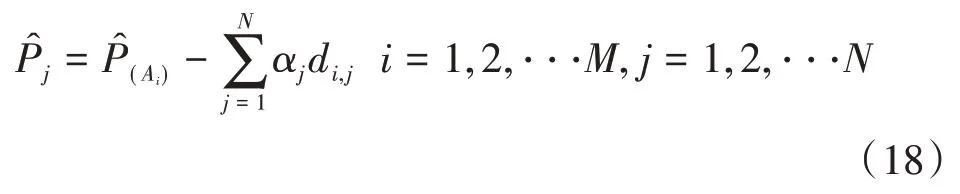
式中：

Pˆ(Ai)——测试区域边界Ai处的信号强度

式（18）表明接收点强度为发射点场强减去各网格上的衰减总和。

信号场强地图中保存了多种信息，包括信号样本强度、位置等。假设室内AP 点个数为S，则信号强度矩阵可记为：RSSI=(rssi1,⋅⋅⋅,rssiu,⋅⋅⋅,rssiS)，其中该矩阵中的每个列向量可以具体写为rssiu=(rssiu,1,⋅⋅⋅,rssiu,j,⋅⋅⋅,rssiu,N)T，其中，u=1,⋅⋅⋅,S，代表AP 个数，j代表网格Gj(j=1,⋅⋅⋅,N)，场强地图的参数矩阵形式为：

其中xj,yj(j=1 ⋅⋅⋅N)为场强地图中第j个网格的位置坐标。

2 在线阶段

经过建立好场强地图后，接收终端在线可获得最新的信号强度等数据，经滤波及相关处理后，采用匹配算法进行匹配与定位。

2.1 传统的在线匹配算法

传统的定位匹配算法常采用基于欧几里德距离的思想，计算实测均值与场强地图中对应值的差值，将差值最小的点作为定位点。

假设第u个AP 发射信号时，在线测得的Q位置处RSSI 均值为,u=1,⋅⋅⋅,S，求得距离Lu，其表达式为：

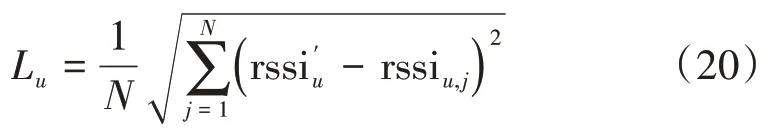
对信号强度进行初步过滤，计算满足该条件的欧氏距离：

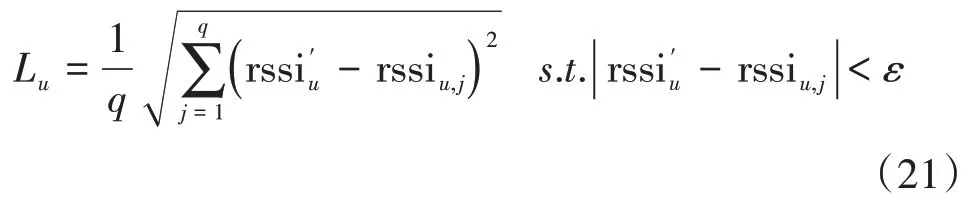
记录满足式（21）的位置Gj、对应场强地图中信号强度值rssiu,j、以及坐标(xj,yj)，并将坐标重新排序整理为（xj，y）j，j=1，⋅⋅⋅，q。如果Lu大于阈值，则调整缩小ε，并刷新记录。假设在线需要测量的实际位置为，通过式（21）计算后，将记录的位置与实际位置进行对比，得到最终位置信息。

目前广泛应用的匹配算法是KNN（K Nearest Neighbor）［18］，WKNN（Weight K Nearest Neighbor）［19］以及DC-WKNN（Differential Coordinates-WKNN）［20］。但是这些算法在复杂的室内环境中存在以下2个问题。

a）定位中人员走动、门开关都会引起某些RSSI发生巨大波动，导致求得的近邻坐标与实际的坐标产生较大误差，但是上述的几种算法中没有对坐标误差进行约束，因此这种影响仍然存在。

b）当AP 信号受环境影响尤为严重时，对接收端接收到的RSSI 影响较大，因此需要考虑AP 点的权重性问题，而上述算法在计算距离时，对各个AP 的处理一样，没有考虑到这个问题。

针对上述2 个问题，本文提出一种加权差分坐标K最近邻法（WDC-WKNN——Weight Differential Coordinates-WKNN）。

2.2 改进的在线匹配算法

针对2.1 节中指出的在线匹配过程中存在的问题，本节提出的WDC-WKNN 算法主要进行了2 个方面的改进。

改进一是设置单个AP 所测得的坐标误差门限ζ，要求测得的坐标误差小于门限值，如果不满足要求，则舍弃并重新匹配。该门限值的设置主要解决当单个AP 的RSSI 波动较大时，导致变大，使得求(x,y)时误差变大的问题。

改进二是对于稳定的和某些受环境影响尤为严重的AP信号，根据影响大小设置AP权重系数。

由式（21）测得的满足条件坐标可分别求与实测位置的误差值，表达式为：

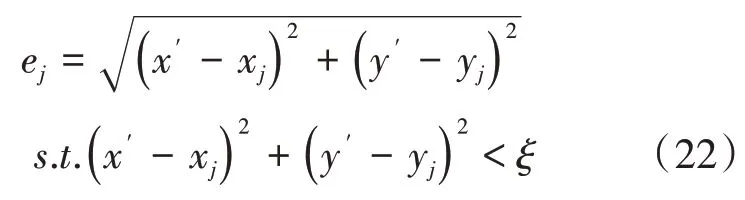
记录满足式（22）的坐标个数q、误差ej及位置(xj,yj)，并按照误差大小重新排序整理为（xj，yj），j=1，⋅⋅⋅，q。第u个AP点发射信号时，估计出的相应坐标为：

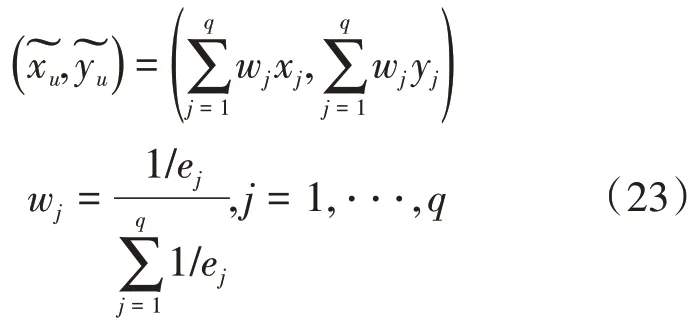
其中，wj为满足条件的q个坐标的权重系数。

针对改进一，增加门限值ζ。由公式（23）计算出后，如果，说明此次测量误差较大，则删去由式（22）记录的坐标（xj，yj），j=1，⋅⋅⋅，q中误差最大的一个数值，并重新计算式（23）得到，直至满足

针对改进二，考虑AP 的权重问题，对于S个AP点，估计的坐标为：

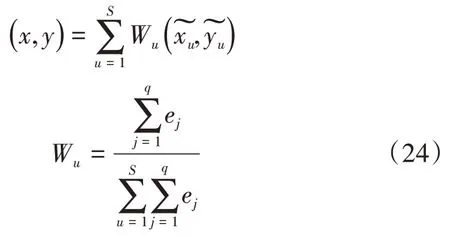
其中，Wu为第u个AP 的权重系数。坐标的绝对误差计算表达式为：

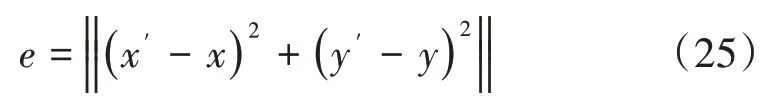
最后，总结出WDC-WKNN算法步骤如表3所示。

表3 WDC-WKNN算法

由于场强地图在线匹配都是线性匹配，所以此阶段的算法的复杂度都相同。另外，由于该算法为匹配算法，只要选择并调整合适的ζ值，一定能满足条件，因此能实现快速收敛。

3 实验结果评估

3.1 仿真环境

设在室内布置3 个AP 点，仿真的室内环境是10×10 m，模拟测试区域如图2所示。

图2中，格子中的方框代表采样点位置，三角形代表AP点位置。

3.2 仿真结果比较

为了比较本文所提的PCG 算法与传统ART、CGM、Jacobi、OMP算法的性能，分别使用这5种算法求解衰减因子，并且比较场强地图中RSSI 的值与实测RSSI 的值。为了不重复性展示，选AP2 作为场强地图的详细分布显示。AP2 发射信号时，仿真的RSSI 覆盖情况如图3所示。

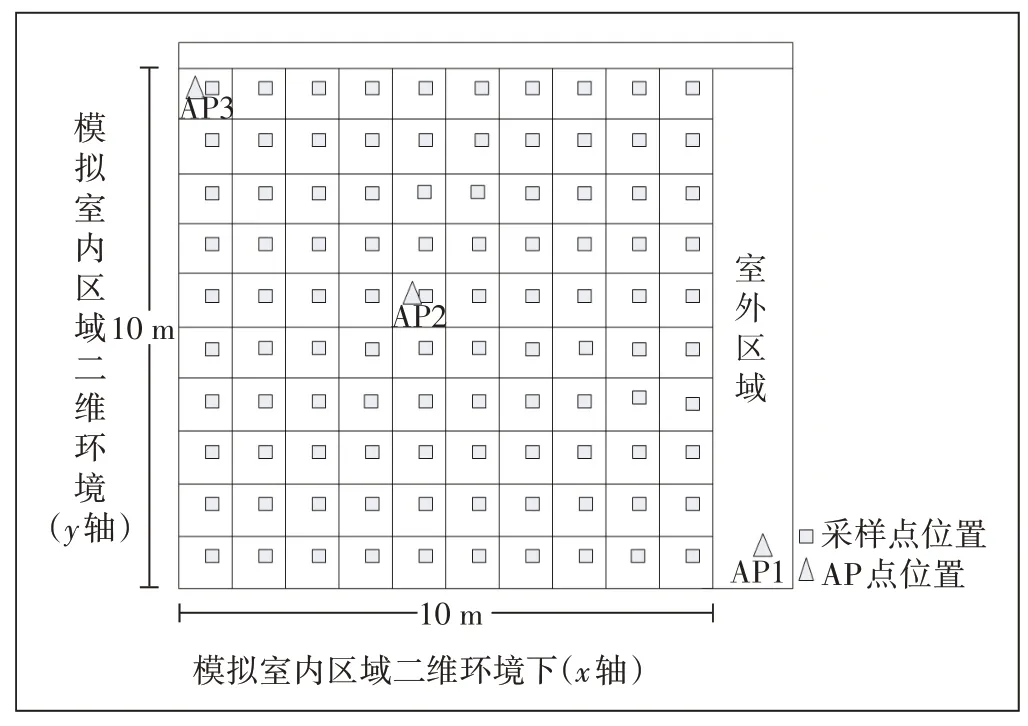
图2 测试区域平面图

图3（a）、（b）、（c）、（d）、（e）为分别采用ART、Jacobi、CGM、OMP、PCG 算法求解衰减因子并得到的RSSI值。可以看出，相比于其他算法，PCG 算法计算衰减因子后得到的RSSI值噪点较少，因此本章提出的PCG算法更接近于室内环境。

考虑3个AP发射信号时，图4 为ART、Jacobi、CGM、OMP、PCG 算法求解衰减因子后，得到的RSSI值分布情况与参照组进行对比的误差分析图。

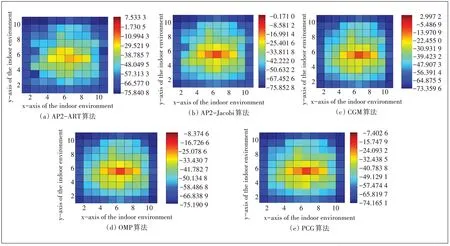
图3 5种算法计算出的RSSI值

图4 中，横坐标是场强地图中的RSSI 与样本均值的误差绝对值，纵坐标是误差百分比。当绝对误差为3 dB，AP1 发射信号时，PCG 算法对应曲线高于OMP、CGM、Jacobi、ART 对应曲线分别约为14%，46%，54%和56%；AP2 发射信号时，PCG 算法对应曲线高于OMP、CGM、Jacobi、ART 对应曲线分别约为8%，22%，24%和26%；AP3 发射信号时，PCG 算法对应曲线高于OMP、CGM、Jacobi、ART 对应曲线分别约为6%，14%，24%和28%。由此说明PCG 算法所求出的信号强度误差比其他算法所求出的信号强度误差小，可以得出PCG 算法计算出衰减因子后，构建的场强地图中RSSI覆盖效果更好，准确度较高。

可以看出，AP2 在室内中心位置，计算出的RSSI误差最小，AP1 在室外，AP3 在室内边角位置，计算出的误差相对较大。可以得出，当AP 在室内的时候，PCG 算法相对于其他算法，构建场强地图的效果更好；当AP 点在室外的时候，虽然PCG 算法计算出衰减因子后误差增大，但构建的场强地图中RSSI覆盖效果也优于其他算法。

3.3 定位效果评估

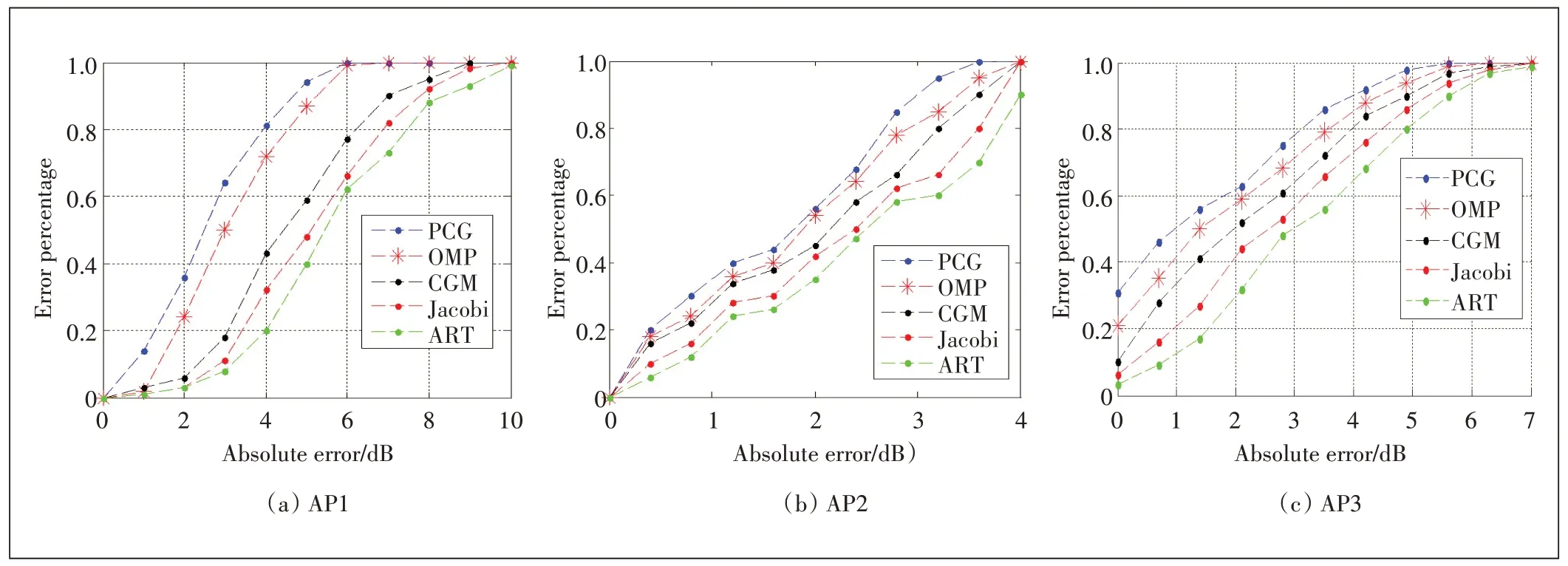
图4 不同AP发射信号时RSSI误差分析图

为了评估本文提出的PCG 算法以及WDC-WKNN算法与传统匹配算法的效果，利用PCG 算法求解衰减因子并构建场强地图，然后利用结合WDC-WKNN 算法和传统的WKNN、DC-WKNN 算法进行在线定位匹配的误差比较如图5所示。

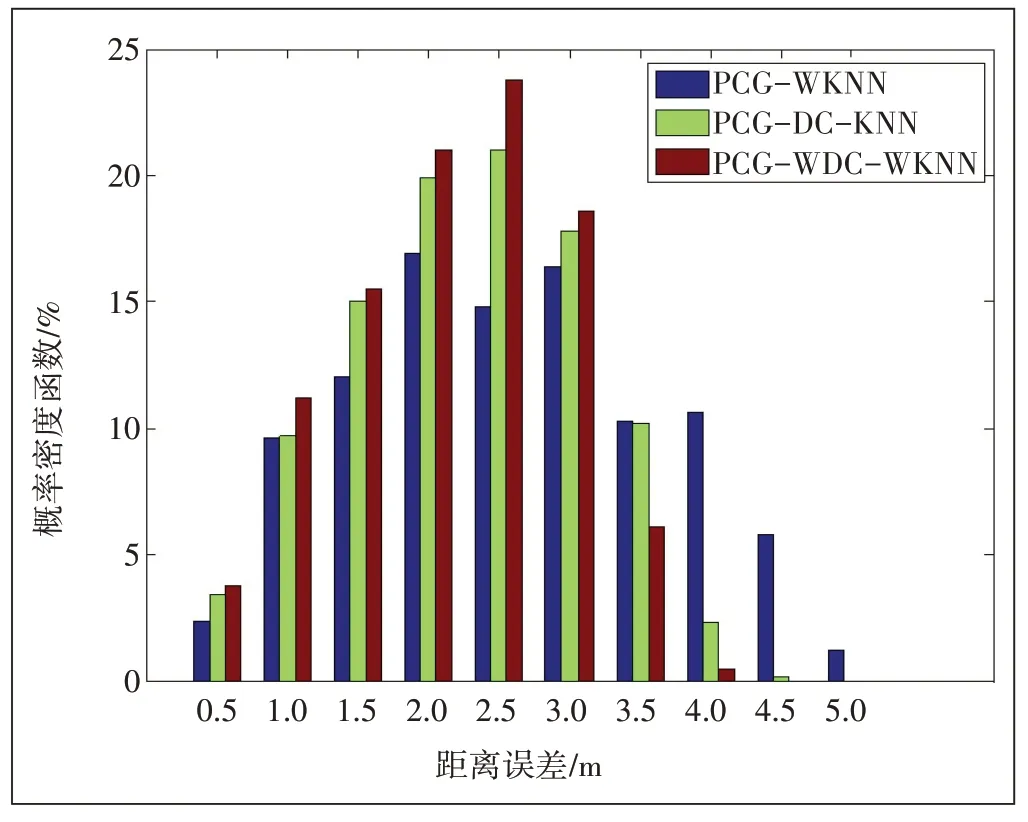
图5 不同方法进行在线匹配的PDF误差

从图5 可以看出，误差在3 m 的时候，PCG-WDCWKNN 算法对应的柱形图高度比PCG-WKNN、PCGDC-WKNN 算法对应的柱形图分别约高0.5%，1.5%，表示提出的WDC-WKNN 算法比传统的匹配算法定位效果好，精度高。

为了更直观地分析本文提出的WDC-WKNN 算法的性能，仿真得到PCG-WDC-WKNN、PCG-DCWKNN、PCG-WKNN 算法进行定位的误差CDF 曲线图，仿真图如图6所示。

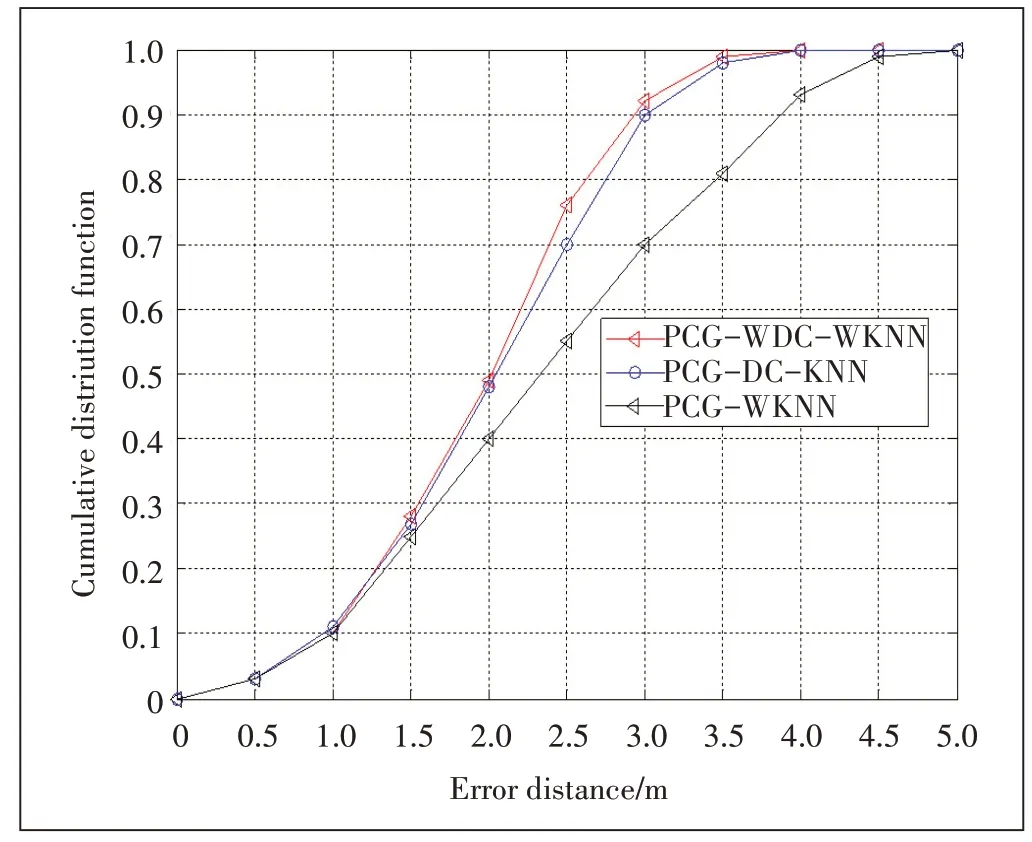
图6 不同方法进行在线匹配的CDF误差

从图6 中看出，当都采用PCG 算法求解衰减因子得到场强地图时，PCG-WDC-WKNN 算法的定位误差在3 m以内的点约占95%，定位误差在2 m以内的点约占50%。而PCG-WKNN、PCG-DC-WKNN 算法的定位误差在3 m 以内的点分别约占90%，70%，定位误差在2 m 以内的点分别约占45%，40%，另外定位误差超过3.5 m 的概率分别接近3%，20%，可以视为定位完全失败。可以得出PCG-WDC-WKNN 算法与PCGWKNN、PCG-DC-WKNN 算法相比，定位效果较好，本章提出的WDC-WKNN 定位匹配算法比传统匹配算法的位置定位准确。

4 结束语

本文采用了基于电磁传播反演模型进行定位。针对离线阶段采集场强工作量大的问题，本文提出了PCG 反演算法，通过实验得到场强地图的结果可以看出，本文算法建立的场强地图和传统算法相比，场强信号误差均有减小。在线阶段，针对AP 信号受环境影响尤为严重的问题，本文提出了改进的在线匹配WDC-WKNN算法，仿真结果显示该算法在3 m以内的累积误差分布明显高于传统算法，说明该算法能很好地将误差范围进行有效控制。所提的仿真实验方法也加强了工程与科研人员对电磁传播的学习与应用。