数学建模在沼气工程中的应用
2020-05-14宋静,邱坤
宋 静, 邱 坤
(1.成都工业职业技术学院, 成都 610213; 2.农业农村部沼气科学研究所, 成都 610041)
1 数学建模方法简介
1.1 回归模型
回归模型主要研究多个影响因素对目标函数的影响(研究变量之间的关系)。具体的做法是:首先收集大量的数据,对数据进行筛选(画出散点图),剔除无效数据;对数据的统计进行分析(首先确定选择函数公式的类型),利用最小二乘法建立数学模型(方程组)并求解得到回归方程的表达式,之后再对回归模型进行显著性检验(相关系数检验、F检验法、残差分析等);上述步骤也可采用SPSS统计软件、MATLAB等数学、统计软件进行。回归模型包括:线性回归模型(一元线性回归模型、多元线性回归模型)和非线性回归模型(一元非线性回归模型、多元非线性回归模型)[1]。
以多元线性回归模型为例:设因变量为y,影响因变量的因素(自变量)为x1,x2,x3,…,xn,误差项为ε,建立方程:
y=a0+a1x1+a2x2+…+anxn+ε
(1)
式中:a0,a1,a2,…,an为模型参数
1.2 BP神经网络
1986年,由Rumelhart和McClelland提出的多层前馈神经网络。通过采用一种误差反向传播算法(BP算法),算法的原理为:利用输出后的得到误差来估计输出前面一层的误差,再用这个误差估计更前一层的误差,按照此规律进行,一层层传递下去,从而获得所有各层的误差估计,我们可以根据各层的误差来修正各层的权值[2]。通过多次迭代计算,实现实际输出与期望输出的差别在可以接受的误差范围内。BP神经网络的学习过程包括: 1)正向传播:样本输入→输入层→各隐层→输出层; 2)判断是否转入反向传播阶段; 3)误差反传——通过各层的误差,修正各层的权值。下面以简单BP神经网络(3层)为例(见图1):

图1 3层神经网络范例图
建模方程:
(2)

1.3 层次分析法结合模糊综合评价
层次分析法是指对决策问题按照总目标、各层子目标进行分解;也可按影响决策问题的影响因素(元素)进行逐层分解;通过调研问卷、查阅文献、数据分析等方式对每一层中的元素进行比较(两两之间的重要性进行比较),给出重要性标度(以定量的方式),并以矩阵的形式表示。结合数学软件MALTAB计算出每层各元素的权重。运用层次分析法(计算出各层元素的权重)结合模糊综合评价(对各层元素建立评判集),通过计算得出对总体目标的定量评价[3]。
具体以对某个旅游景点的收益评价为例。
确定3个重要影响因素(例如:游客量、门票价、维护成本),重要性标度为p1,p2,p3,特别说明:重要性标度的值越大说明越重要。以矩阵的形式给出:
2 数学建模方法在沼气工程中的应用
引用已发表文献中的相关数据[4],研究3种因素(pH值,接种量,C/N)对沼气日均产气量的影响。发酵材料选用新鲜猪粪,接种物取自沼气池,是以猪粪为原料富集培养的混合微生物种群,数据见表1。

表1 3种因素对沼气日均产气量的影响
2.1 多元回归模型在沼气工程中的应用
根据表1中的数据,我们研究pH值、接种量和C/N对日均产气量的影响,令pH值,接种量和C/N这3种因素为自变量分别为xi(i=1,2,3),日均产气量为因变量为y。运用线性回归模型建立函数关系式:y=a0+a1x1+a2x2+a3x3,并用数学软件MATLAB求解,得到:
y=0.014x1-0.5706x2+0.5703x3
(3)
特别说明,在采用此方法之前,笔者对收集的数据进行筛查,剔除掉异常点(在实际的计算过程中,笔者发现9组数据中没有异常数据,见图2),再用数学软件MATLAB编写相关程序得到我们的结果,计算出的参数a0,a1,a2,a3均在置信区间范围内。
MATLAB程序:
n=9;m=3;
y=[0.7180 0.7408 0.6064 0.5265 0.5294 0.6486 0.7518 0.6230 0.7325];
x1=[6.0 6.0 6.0 6.5 6.5 6.5 7.0 7.0 7.0];

图2 参数信度图
x2=[24 29 34 24 29 34 24 29 34];
x3=[25 30 35 25 30 35 25 30 35];
X=[ones(n,1),x1',x2',x3'];
[b,bint,r,rint,s]=regress(y',X);
s1=sum(r.^2) /(
n-m-1);
b,bint,s,s1
rcoplot(r,rint)
2.2 BP神经网络在沼气工程中的应用
根据表1中的数据,可以运用BP神经网络预测在不同条件下(pH值、接种量和C/N 3种因素确定)的日均产气量,从而可以研究不同因素条件下对日均产气量的影响(见表2)。

表2 不同因素条件下对日均产气量的影响
根据表2的数据计算:当pH值=7.5,接种量=24%,C/N=25时,预测得到日均产气量=0.6633。
MATLAB程序:
P=[6.0 6.0 6.0 6.5 6.5 6.5 7.0 7.0 7.0;24 29 34 24 29 34 24 29 34;25 30 35 25 30 35 25 30 35];
T=[0.7180 0.7408 0.6064 0.5265 0.5294 0.6486 0.7518 0.6230 0.7365];
[p1,minp,maxp,t1,mint,maxt]=premnmx(P,T);
net=newff(minmax(P),[3,2,1],{'tansig','tansig','purelin'},'trainlm');
net.trainParam.epochs=5000;
net.trainParam.goal=0.0000001;
[net,tr]=train(net,p1,t1);
a=[7.5;24;25];
a=premnmx(a);
b=sim(net,a);
c=postmnmx(b,mint,maxt);
c
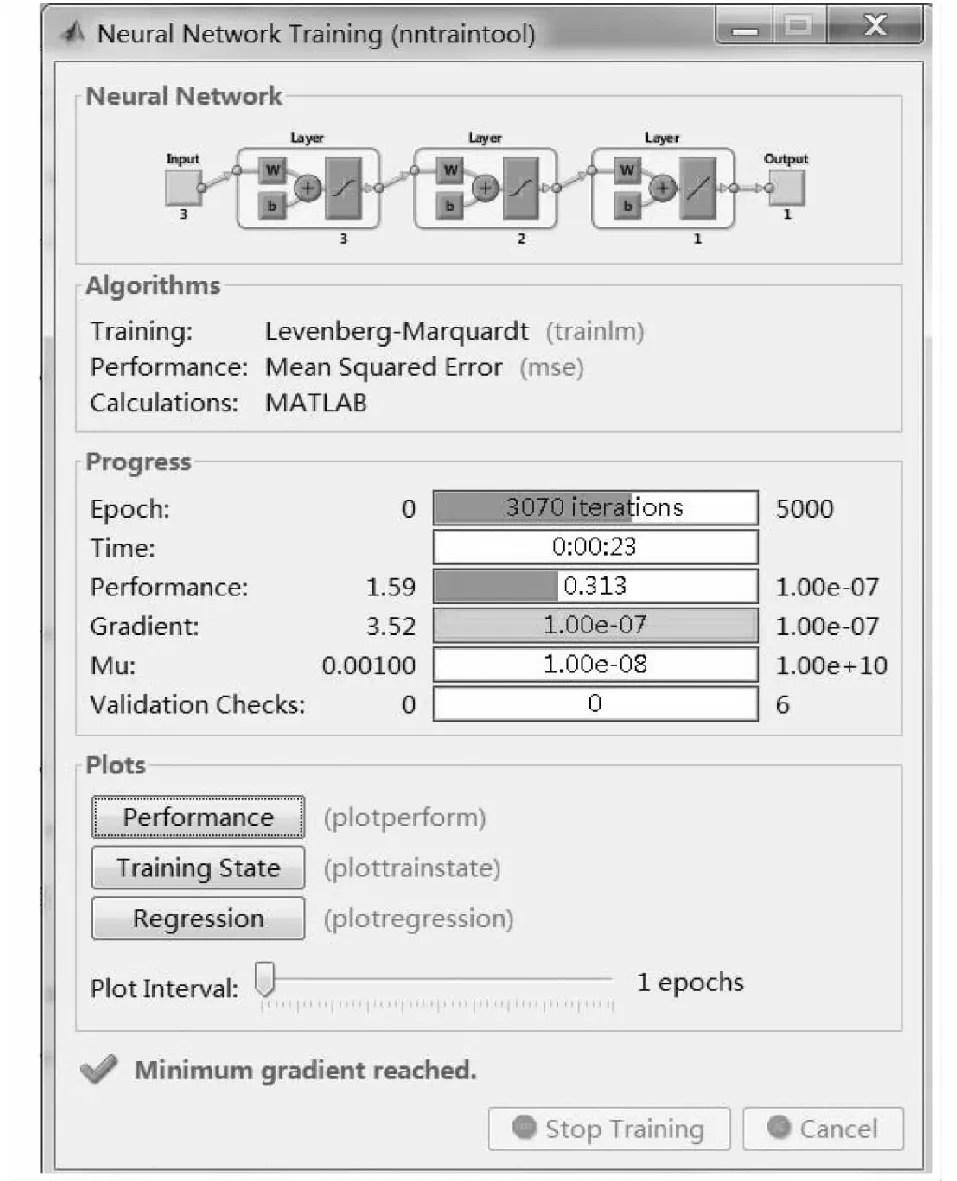
图3 神经网络训练结果图
特别说明:如图3,运用BP神经网络,隐藏层神经元为2,网络迭代次数5000次,期望误差0.00000001,在实际程序的运行过程中第3070次迭代中的计算结果已经在误差范围内。
2.3 层次分析法结合模糊综合评价在沼气工程中的应用
引用已发表文献中的相关数据[5],研究农户满意度指标体系,鉴于本文侧重于介绍数学模型(层次分析法结合模糊综合评价)在沼气工程中的应用,因此,建立层次结构模型时仅选用部分指标。
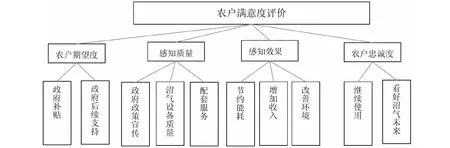
图4 农户对沼气项目评价多层次结构分析图
根据层次结构模型及参考文献中的相关数据,建立各项指标评判集及满意度评价表。
农户满意度评价集(元素集):
W={w1-w2-w3w4}=
{农户期望度、感知质量、感知效果、农户忠诚度}
每一个一级指标下设立二级指标,并对每个二级指标的满意度进行评价,详见表3。
特别说明,在选择表中数据时的依据更多根据文献中各项指标的得分率。例如,文献中提到农户愿意继续使用的得分率为90.4%,因此,评价“好”与“较好”两者的比例和为90%。鉴于文献可用数据较少,文章更侧用于介绍数学模型的应用,后面3项“一般”、“较差”、“差”的比例的和满足为10%(通过估计算得出)。此外,每项指标的比例参照上述方法估算得到。
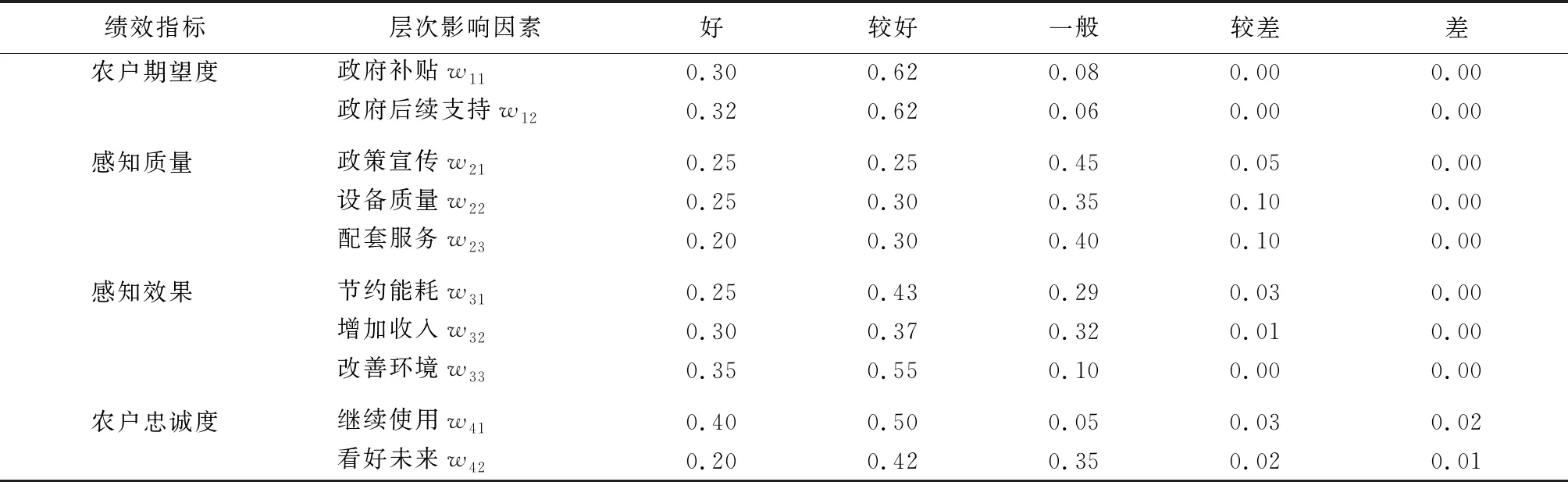
表3 农户满意度评价表
对各级指标的权重进行定义,建立模糊评价矩阵,并计算矩阵的权重:

一级指标:农户期望度、感知质量、感知效果、农户忠诚度建立模糊评价矩阵:
计算矩阵的权重W:
这里可考虑:
计算出的权重:
即:各种因素(同层次)的重要性均是一样的。
对于某些实际问题,特别是在各因素权重不同时,也可采用MATLAB程序实现,通过运行相关程序,输入权重矩阵,即可计算出各因素的权重。
MATLAB程序:
clc;
clear;
disp('请输入判断矩阵A');
A=input('A=');
[m,n]=size(A);
RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51];
R=rank(A);
[V,D]=eig(A);
tz=max(D);
B=max(tz);
[row, col]=find(D==B);
C=V(:,col);
CI=(B-n) /(
n-1);
CR=CI/RI(1,n);
if CR<0.10
disp('CI=');disp(CI);
disp('CR=');disp(CR);
disp('对比矩阵A通过一致性检验,各向量权重向量Q为:');
Q=zeros(n,1);
for i=1∶n
Q(i,1)=C(i,1)/sum(C(∶,1));
end
Q
else
disp('对比矩阵A未通过一致性检验,需对对比矩阵A重新构造');
end
根据表3中的相关数据,得到评价矩阵:
结合二级权重矩阵,通过计算得到二级模糊评级矩阵:
B1=W11×R11=0.31 0.62 0.07 0 0
B2=W12×R12=0.2333 0.2833 0.4 0.0833 0
B3=W13×R13=0.3 0.45 0.2367 0.0133 0
B4=W14×R14=0.3 0.46 0.2 0.025 0.015
得到R:

因此,R=W×R=[0.2858 0.4533 0.2267 0.0304 0.0037],得到一级模糊评价矩阵。
通过上述例子可以看出,农户对于沼气工程的满意度从农户期望度、感知质量、感知效果、农户忠诚度四个方面进行评价,28.58%认为很好,45.33%认为较好,22.67%认为一般,认为较差和很差的分别仅占3.04%和0.37%。
3 小结
数学模型的运用有助于解决沼气工程中的许多问题。包括研究产气量与各因素之间的关系;预测在某些已知参数条件下的沼气工程的产气量;对沼气工程进行定性和定量的评价等。运用数学模型,可以让我们的结论更具有说服力,同时,也可根据模型的一些结果反推去解决沼气工程中出现的一些技术问题,查找理论与实际值出现差异的原因。本文主要介绍了常用的3种数学模型在沼气工程中的应用(重点在于方法的介绍与应用),由于选用的部分文献提供的数据有限,部分数据根据已有数据估算得到,模型与实际结果存在一定的差异性。
