发展学生数学思维之策略谈

蒋依宝

【摘   要】小学数学教学过程是学生数学思维培养的过程，教师在教学中要重视思维材料的组织，并尽可能“动态”展现。同时还要关注过程合适、材料合适、问题合适，帮助学生建立合适的认知结构，学习相应的策略性知识。

【关键词】数学思维;教学;策略

小学数学的教学内容，是小学生数学思维培养的载体。学生在解决问题时，存储在头脑中的知识会被激活，并根据需要被提取出来，参与到当前的思维活动之中。不同的学生有着不同的认知结构，如果其认知结构的区分度、清晰度高，就能方便知识的提取。所以，小学数学教学的一个非常重要的任务就是不断完善学生的认知结构，优化学生的数学思维活动。教师在教学中要重视思维材料的组织和动态展现，适配学生的思维过程。

一、合适的过程促学生全程参与

由于结果性的数学知识在教材中占有很大的比例，教师如果对教材不做教法的加工处理，直接呈现给学生，就不利于学生数学思维能力的培养。因此，教师应该深入钻研教材，把“教本”变为“学本”，把“静态”的数学知识变成“动态”的数学教学。如“两位数乘法”的教学，教师这样安排：

1.呈现情境，引出算式。提问：今天是3月27日，三月有31天，三月有几小时？

2.问题驱动，自主探究。①提出挑战性的问题：31×24是两位数乘两位数的乘法，我们没有学过，谁能用尽可能多的方法来计算？②组织探究：个体探究→小组交流→班内展示。形成多种算法：同数连加、连乘、两积之和、两积之差、列竖式。

3.引导比较，优化算法。①从解决问题的角度看，这些算法有何共同点？②从适用范围、计算是否方便的角度看，哪些算法比较好？

4.沟通联系，教学竖式。①比较“两积之和”与“列竖式”，后者是前者的另一种表示形式，前者是后者的算理。②借助算理，简化竖式。

教学中教师提供的过程性学习材料发挥了重要作用，在探索算法的过程中，学生参与度高，组内交流基本形成解题方法，班内展示产生了多种方法。从反馈情况看，不同学生的算法体现思维的差异性与层次性，通过比较“两积之和”与“竖式计算”，明白了竖式的算理。学生也由此悟出了解题策略——把“新”问题转化为“旧”问题来解决。

二、合适的材料促学生自主探究

教材为教师提供了“教”材，而学生是探究的主体，所以需将“教”材转化成供学生探索的“学”材。教学中教师要给学生留有时空，让他们经历探究的过程，使其明白：数学是如何提出问题的？数学又是怎样得到结论的？如教学“三角形面积”，有教师这样安排：

1.提供格子图，初步探究。 ①呈现方格图（各类型三角形各1个），提出问题：如果每个小方格的边长是1厘米，你能求这三个三角形的面积吗？请把想法画在图上，并将算式写在旁边。②引导探究：个体探究→小组交流→班内展示。反馈交流：数格法;剪拼法，如何剪拼？扩倍法，为何这样补？初步得出：三角形面积=底×高÷2。

2.特殊到一般，深入探究。 ①提问：是否所有三角形都这样？没有了格子图，能验证吗？②组织探究，上台展示。一是说方法和操作过程，说转化的图形与原三角形的关系;二是重点反馈锐角三角形的各种转化;三是适当借助课件帮助理解;四是找与底对应的高，从而明确面积公式。③比较分析：上面的验证方法有什么共同特点？（“新”转化为“旧”）在实际操作时往往无法剪拼，怎么办？（脑中想象）④归纳结论：对不同材料采用不同操作方法进行验证，得到同一结论。

教学中，教师通过创设问题情境，引发学生“新”“旧”认知的冲突，推动其不断探索。第一个环节，借助格子图，让学生初步认识三角形面积计算方法。第二个环节，学习材料为任意三角形，从特殊到一般，学生“八仙过海，各显神通”，上台展示有话可说。学生活跃的思维，来自教師提供的开放探究型问题。随着交流的深入，学生取长补短，从群体中获得自己所需要的信息，形成新认知。

三、合适的问题完善学生的知识表征

许多学生在应用数学解决问题时感到很茫然，不知道如何运用学到的知识去解决问题。教学材料丧失“活力”使学生的知识逐渐僵化。因此，教师在教学时要让学生知道知识的来龙去脉，将所学知识与该知识应用的条件联结起来。

如人教版三年级上册的“归一问题”：妈妈买3个碗用了18元。如果买8个同样的碗，需要多少钱？大多数教师这样教学：先完整地呈现问题，再借助线段图等直观手段表征问题，分析数量关系。但学生中出现了共性问题——为什么要先算出一个碗多少钱？因此，有必要在教学中创设生活情境，以增强知识的“活性”，采用动态的方式呈现学习材料，让学生在头脑中建立起数学知识与应用问题的联系，提高数学知识在解决问题中的“适用性”。一位教师这样教学：

师：三年级在下周举行拍球比赛，我班要预测成绩。老师想很快地测算出全班41个同学在1分钟内大约能拍几下，应该怎么做？

生：先测出每个同学1分钟拍的数量，再相加。

生：这样太麻烦。只要测出一个同学1分钟拍的数量，再乘41就行了。

生：这样不准确！因为这个同学可能拍得很快，也可能拍得很慢。

师：请想出一个既快又可靠的办法。

经过讨论，一学生建议：先测算出一组同学（5人）1分钟拍的数量，算出平均每人拍的数量，再乘41。

组织拍球后统计数据，编出问题：5个同学在1分钟内共拍球150下。照这样计算，全班41人1分钟大约能拍几下？

解题后，教师引导小结，引发联想：用这种方法推算，能预测并解决日常生活和生产中的许多问题，如……

以上教学，结合熟悉的情境，动态呈现学习材料，能让学生了解数学知识的实际应用背景，使知识条件化，得出解题思路和方法也就水到渠成了。

四、合适的认知结构促学生思维发展

在解决问题时，學生要在数以万计的知识“联系组合”中找出与眼前问题相匹配的“条件”，有一定难度。因此对知识块再次进行组合，形成一个系统，对学生而言十分必要，学生可借助系统中部分与整体、部分与部分的联系提高检索效率，促进思维发展。

如“20以内进位加法”这一教学内容，教材将36道计算题分布在不同课时，要求学生在看到或听到算题后，就能够脱口而出得数，分散的学习使学生很难达到要求。但“20以内进位加法”是小学数学知识体系中的子系统，一个系统就是一个整体，任何整体都是由各部分按照其本身所固有的规律构成的。因此，教师可设计一节复习课，让这一板块发挥整体结构的功能。

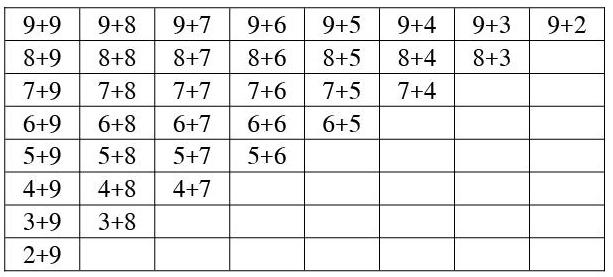
1.自主梳理知识：20以内进位加法有哪些？你想按怎样的顺序把算式写在空表内？

2.班内展示汇报，说出整理的思路。

3.出示下表，引导找规律，从而沟通联系。①从得数与加数的比较中找出9加几……的规律。②横着看、竖着看、斜着看，找出规律。③从分析数的奇偶性（单、双数）入手，找出规律。④根据“两数相加，交换位置，得数不变”的规律找出得数相同的式子，去掉重复的，剩下20道。

4.组织练习。一是看算式说得数，说说是怎么想的，从而强化规律;二是对易错的7+6和7+5重点练;三是同桌合作练习。

五、合适的策略性知识培养学生良好的思维品质

教师要重视对学生解决问题策略的指导，使学生具有一定的策略性知识。这种“策略”的教学要结合具体学习情境有意传授、训练，持之以恒，使学生能有意识地运用策略性知识。

一要遵循“由外到内”的教学规律。即先由教师有目的地根据具体教学情境，引导学生把策略性知识运用到问题解决之中，再激励学生在类似的情境中应用练习。如当学生在运用割拼转化得出平行四边形面积公式后，教师要及时提出：把一个图形转化为与它面积相等的另一个图形，叫作等积变形，等积变形是一种解决数学问题的策略，在学习中会经常用到，请密切关注。学生掌握了这一策略性知识，在三角形、梯形面积计算的学习中就会自觉地运用。

二要让学生评价自己所运用的策略的优劣，同学之间互相启发，逐步完善策略。如“两位数乘法”教例中，用多种方法计算31×24后，教师留下时空，引导学生进行比较，从解决问题的角度寻找各种算法的共性，从适用范围、简易程度等角度，对所有方法进行评估，优化算法。

三要根据学生年龄特征逐步培养。不同年龄段学生的认知水平是不相同的。各年级问题解决策略的培养要有侧重点，从低年级开始逐步培养，使学生渐渐地感受应用问题解决策略的“好处”。同一策略须在不同年级进行螺旋式应用，以便学生切实掌握。

参考文献：

[1]周玉仁.周玉仁优化小学数学教学文集[M].福州：福建教育出版社，1993.

[2]陈英和.认知发展心理学[M].杭州：浙江人民出版社，1996.

[3]成尚荣.学会数学地思维[M].南京：江苏教育出版社，2001.

（浙江省临海市教育局教研室   317000）