循环冲击荷载下花岗岩力学特性尺寸效应

2020-05-12王志亮卢志堂巫绪涛

水利水运工程学报 2020年2期

章航，王志亮，卢志堂，熊峰，巫绪涛

(1. 合肥工业大学土木与水利工程学院，安徽合肥 230009；2. 合肥工业大学资源与环境工程学院，安徽合肥230009)

岩石是由多种矿物组成的地质材料，在其形成后经历了风化作用和构造作用，内部含有大量不同尺度的裂纹和孔隙[1]。在地下隧硐、矿山等爆破开挖中，围岩体承受循环冲击载荷作用，不同尺寸的岩石块体内部裂纹会发生起裂、扩展、贯通直至表现为宏观的失稳破坏[2]。花岗岩作为一种分布非常广泛的岩石，在水利水电、安全防护等工程中涉及较多。因此，研究循环冲击载荷对不同尺寸花岗岩块体损伤演化过程中力学特性的影响具有重要意义。

近年来，国内外学者对岩石力学特性的尺寸效应开展了大量研究工作。彭剑文等[3]通过对等比例尺寸的砂岩试样进行三点弯曲试验，发现随着试样尺寸增大，名义抗拉强度减小，而断裂韧度和破裂区范围呈增大趋势；平琦等[4]对12种规格的石灰岩试样（直径50 mm，长度15～100 mm）进行了循环冲击试验，发现石灰岩试样单轴动态抗压强度存在明显的尺寸效应，动态抗压强度随试样长度增大呈先增后减的趋势，且在试样长度为60 mm时强度最大；王连山等[5]对大理岩、闪长岩和凝灰岩进行了单轴抗压强度试验，发现其单轴抗压强度随高宽比增加先减后增，对应的破坏形式为复杂劈裂、劈裂和剪切破坏；杨圣奇等[6]对同直径不同长度大理岩开展了单轴压缩试验，指出岩石长度对峰值应力前的变形特性没有显著影响，但明显改变峰后的变形特性，且直径一定时，随着长度增加，岩样破裂形式由竖向劈裂变为剪切破坏；高富强等[7]对不同高径比的石灰岩试样进行了准静态和动态冲击压缩试验，指出动态冲击条件下，试样高径比对强度的影响存在一个临界值；刘宝琛等[8]对7种岩石进行了单向抗压强度试验，研究了岩石抗压强度的尺寸效应；梁正召等[9]基于物理力学试验和微观参数统计理论，建立了完整的岩石尺寸效应统计模型；李建林等[10]研究了卸荷岩体尺寸效应对应力-应变曲线、抗压强度、变形模量等的影响；洪亮等[11]对不同尺寸砂岩和石灰岩试样（直径分别为22, 36和75 mm，长度恒定）进行了SHPB试验，发现在相同应变率下岩石动态强度随试样尺寸的增大而增大，这与静载荷条件下的尺寸效应相反，且岩石动态尺寸效应随着应变率降低而逐渐变弱。

综上可知，现有研究多集中于静态压缩或单次冲击下岩石力学特性尺寸效应的分析，对循环冲击作用下岩石物理力学参数、破坏模式与能量耗散等演化及其尺寸效应研究比较少。为了加深对循环冲击时岩石力学特性演化及尺寸效应的认识，本文拟通过对黑云母花岗岩进行循环冲击试验，分析试样的动态应力-应变曲线特征，确定其力学参数的演化规律，探讨高径比对试样的破坏模式、耗能特性等的影响。

1 试验介绍

1.1 试样制备

本次试验采用的试样取材于湖南汨罗，岩样呈灰白色，属于中细粒黑云母花岗岩。其平均密度为2 600 kg/m3，主要含微斜长石(40%)、斜长石(26%)、石英(22%)、黑云母(7%）等矿物。为分析循环冲击作用下花岗岩力学特性及其尺寸效应（考虑试样高度变化），特制备了3种规格的试样，分别为Φ50 mm×50 mm，Φ50 mm×38 mm和 Φ50 mm×25 mm，编为H，M和 B组 (见图 1)，对应高径比依次为：1.00，0.76和0.50。试样端面不平行度控制在0.05 mm以内。试验前，结合波速测试对试样进行了严格筛选，以减小离散性。

图 1 典型花岗岩试样Fig. 1 Typical granite specimens

1.2 试验设备

试验采用SHPB测试系统(图2)，主要包括气压室、子弹与压杆(入射杆、透射杆和吸收杆)、采集设备(超动态应变仪、瞬态波形存储器与数据采集仪)。压杆为高强度40Cr合金钢，纵波波速为5 172 m/s，弹性模量为210 GPa，入射杆、透射杆长度分别为2 400和1 200 mm，其中入射杆采用直锥变截面形式，直径由Φ37 mm渐增到Φ50 mm。为消除加载波形P-C振荡，在入射杆前端中心粘贴圆形橡胶薄垫片，达到钟形波加载的目的。

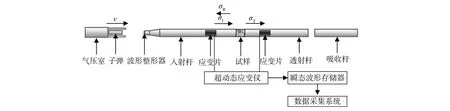
图 2 SHPB系统示意Fig. 2 Schematic drawing of SHPB system

1.3 试验原理

根据图2所示，试验过程中高压气体推动子弹以一定速度与入射杆对心碰撞，产生的入射应力波σI传播至试样与压杆接触的交界面后，产生反射应力波σR和透射应力波σT。入射杆表面应变片测量出入射和反射应变信号，透射杆表面应变片测量出透射应变信号。根据一维应力波理论，可以计算出试样平均应变、平均应变率和平均应力，其计算式为：

式中：A，AS分别为压杆横截面积、试样横截面积（mm2）；l0为试样长度（mm）；E 为压杆弹性模量（GPa）；C0为压杆纵波波速（m/s）；εI，εR，εT分别为入射、反射以及透射波应变信号。

式(1)～(3)就是SHPB试验数据处理的经典“三波法”公式，可得试样的动态应力-应变曲线等结果。

1.4 试验方案

试验中，弹速（即子弹速度）通过调试气压来控制。需保证选取的弹速能达到试样脆性断裂的门槛应力，又不使试样单次冲击就破坏，同时为对冲击荷载幅值的影响进行分析，采用8.5和9.9 m/s两种弹速循环冲击试样。每组弹速下不同高径比试样各做3～5个（各系列高径比试样编为H，M和B组，每组从小到大依次编号），保证试验结果具有良好一致性。

试验步骤如下：（1）先对齐压杆进行空冲（不含试样）：对齐压杆后启动装置，子弹向右撞击入射杆进行加载（见图2）。多次空冲调试气压，使弹速稳定在预定值。（2）将试样夹持在入射杆与透射杆之间进行冲击，每次冲击结束后检查试样状态，直到试样出现明显破碎面时停止冲击，记录此时的冲击次数，即为该试样所受循环冲击次数。（3）对下一个试样进行循环冲击，重复上述操作。

本试验各系列高径比试样直径均为50 mm，只改变了试样高度（H，M和B组高度分别为50，38和25 mm），所以尺寸效应表现为试样高度变化的影响。

2 试验结果与分析

2.1 应力-应变曲线特征

图3和4分别为8.5和9.9 m/s弹速下典型试样的应力-应变曲线。按试样组号、循环冲击次数与平均应变率进行编号（如：图3（a）中B1-1-表示B组编号为1的试样第1次冲击得到的平均应变率，图4（b）图例M2-3-表示M组编号为2的试样第3次冲击得到的平均应变率）。需要注意的是，各个子图中最后一条曲线就是试样破坏时的应力-应变曲线。从图3和4中可以看出：试样未破坏时，应力-应变曲线基本可分为压密阶段、弹性阶段、微裂纹扩展阶段、卸载阶段，且卸载段出现显著的“回弹”现象，表明试样仍具有一定抵抗变形能力，损伤相对不严重；而最后一次冲击时（试样破坏），应力-应变曲线中已无明显回弹。这表明试样产生严重损伤，导致试样破碎。同一弹速下随着试样高径比的减小，最后一次应力-应变曲线的峰后破坏阶段更显著。此外由图3(a)还可看出，随着循环冲击次数增加，B1试样的各个应力-应变曲线上升段斜率逐渐减小，表明弹性模量不断降低。

图 3 弹速8.5 m/s典型动态应力-应变曲线Fig. 3 Typical dynamic stress-strain curves at striking velocity of 8.5 m/s

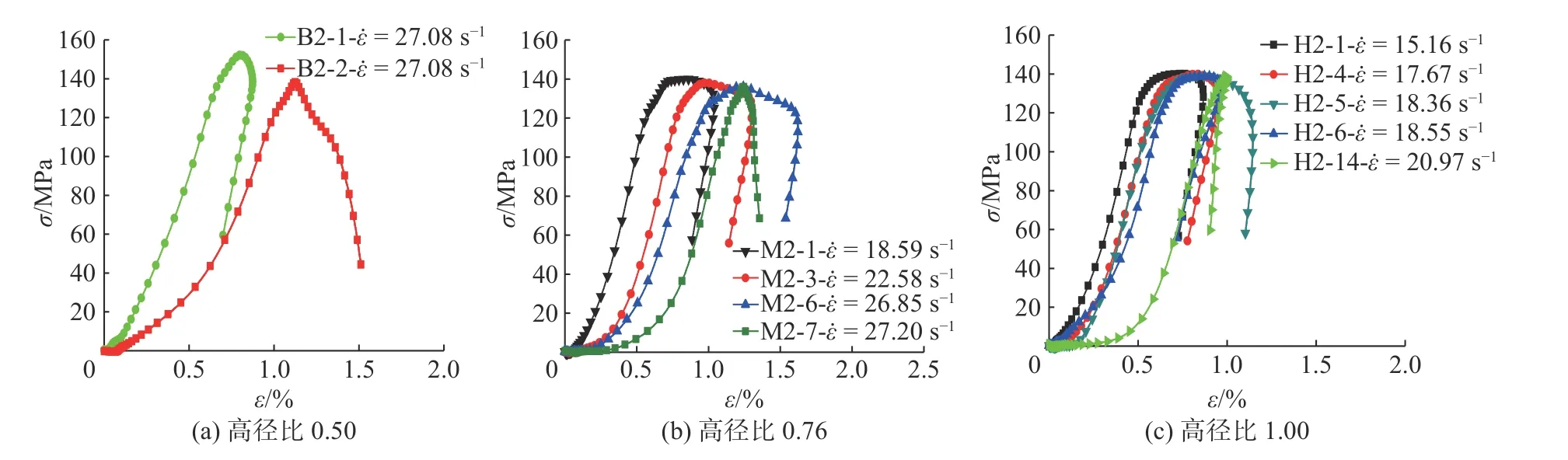
图 4 弹速9.9 m/s典型动态应力-应变曲线Fig. 4 Typical dynamic stress-strain curves at striking velocity of 9.9 m/s

2.2 峰值应力特征

在循环冲击过程中，试样峰值应力随高径比及冲击次数变化趋势见图5(图中S表示拟合数据的均方差)。从图5中可以看出，随着冲击次数增加，峰值应力整体呈下降趋势。图5的拟合线表明峰值应力下降趋势随高径比的减小而增大。其原因可以根据式(2)分析：由于压杆纵波波速为常数，而整体上来看，入射波、反射波和透射波信号基本保持不变，因此当试样高度(l0)减小时，试样平均应变率整体会变大，试样内部产生的裂纹数目增多，造成试样内部损伤加重，从而导致试样性能劣化。

从图5中还可以看出高弹速下(即弹速9.9 m/s)，各系列高径比试样峰值应力下降幅度明显大于低弹速情况(即弹速8.5 m/s)，如B2试样峰值应力随冲击次数近似垂直下降，而B1试样峰值应力则下降较为平缓，原因是高弹速下入射波能量更大，更多的裂纹被激活与延伸，试样力学性能迅速劣化。图5体现了峰值应力对冲击次数具有依赖性，而且在高弹速（或高应变率）条件下，这种依赖性更为明显。

图 5 不同弹速下高径比对峰值应力的影响Fig. 5 Effects of height-diameter ratio on peak stress under different striking velocities

2.3 峰值应变特征

图6为不同高径比下峰值应变（即图3和4中峰值应力对应的应变）与高径比及循环冲击次数的关系。结果表明，相同弹速下随着高径比增加，循环冲击过程中峰值应变整体减小；如弹速8.5 m/s时，随着高径比增加，第2次冲击时B1，M1，H1试样对应峰值应变分别为0.009 8，0.009 2和0.006 8；弹速9.9 m/s下B2，M2，H2试样对应峰值应变分别为0.011 0，0.008 6与0.008 0，原因在于随着高径比增加，冲击载荷下试样平均应变率整体降低。低应变率激活少数微裂纹并扩展，导致试样刚度降低相对缓慢。因此，H组试样（高径比为1.00）经多次冲击后，比相同冲击次数下M，B组试样（高径比分别为0.76和0.50）承受外部冲击载荷的能力强，表现在承受相同大小的应力作用下，试样沿轴向的变形更小，故而峰值应变整体偏小。

此外，从图6（a）中B1，M1，H1试样峰值应变与循环冲击次数拟合直线斜率分别为0.001 44，0.000 643和0.000 338，可见试样的峰值应变与循环冲击次数之间呈正相关，这主要是由于在入射波循环作用下，部分入射波能被试样吸收以弹性势能形式储存在试样内部，而试样的非均质性造成内部应力分布不均匀，容易产生应力集中效应，导致试样内部微裂纹的萌生和扩展。随着循环冲击次数增加，试样内部储存的弹性势能得到释放，造成耗散能逐渐增大，这部分能量直接作用于岩石的压缩变形和破坏上，试样内部更多的微裂纹被激活与进一步扩展，出现不可逆的塑性变形，故峰值应变随之增加。

图 6 不同弹速下高径比对峰值应变的影响Fig. 6 Effects of height-diameter ratio on peak strain at different striking velocities

2.4 弹性模量比较

弹性模量计算可以分为平均弹性模量和割线模量两种方式[12]。由于岩石的动态应力-应变曲线可以划分为多个阶段，试样动态弹性模量可由曲线加载过程中的弹性上升阶段斜率得出，而平均弹性模量的大小与弹性阶段起点、终点坐标的选取有关。起始点和终点坐标选取的不同往往影响弹性模量的大小，因此弹性模量取值结果误差较大，故选择峰值应力50%处对应的点与坐标原点之间连线的斜率（即割线弹性模量），作为衡量动态应力-应变曲线特征的力学参数进行分析：

式中：σ50为峰值应力 50% 应力值（MPa）；ε50为 σ50对应的应变值。

图7给出了试样动态弹形模量与高径比及循环冲击次数之间的关系。由图7可见，动态弹性模量与高径比具有正相关性，即在弹速一定和冲击次数相同时，试样高度越大，弹性模量越大。在循环载荷作用下，大高径比带来平均应变率整体减小，从而延缓甚至抑制了微裂纹的起裂与扩展，造成试样内部累积损伤较小以及整体刚度降低变缓慢，裂纹间的“呲合”作用较显著，故而在循环冲击次数相同情况下，试样的动态弹性模量较大。此外，还可以看出，弹速一定时，试样动态弹性模量均随着循环冲击次数增加而减小。经分析认为随着循环冲击次数增加，试样内部微裂纹处产生应力集中而起裂、成核汇聚或扩展贯通，累积损伤加剧，试样密实度变差，降低了试样组构间传递载荷的能力和比例，导致试样刚度下降。特别是，当岩石内部累积损伤达到损伤阈值时，试样承受载荷能力大幅减弱，宏观上表现为失稳破坏。

图 7 不同弹速下高径比对试样动态弹形模量的影响Fig. 7 Effects of height-diameter ratio on dynamic elastic modulus of specimens at different striking velocities

2.5 吸能耗能特性分析

为探讨循环冲击荷载作用下，不同高径比试样耗能特性与冲击次数之间的关系，引入累积比能量吸收值ϑ，定义为试样在循环冲击过程中单位体积累积吸收的能量。根据能量守恒原理，得出单位体积吸收能、累积比能量计算公式[13]分别为：

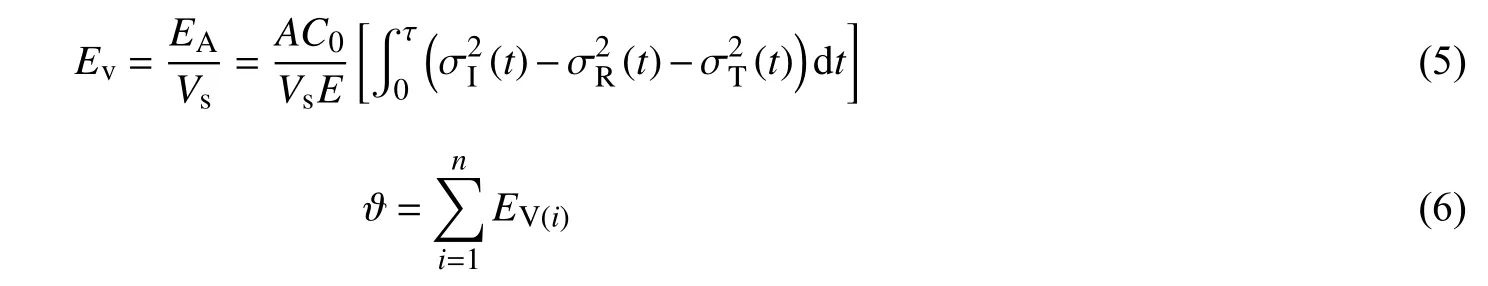
式中：EA，Ev分别为试样总吸收能（J）和单位体积吸收能（J/cm3）；Vs为试样体积（cm3）；τ为试样从加载至破坏所需时长（μs）。

图8给出了试样累积比能量随高径比与循环冲击次数变化的关系。

图 8 不同弹速下高径比对累积比能量值的影响Fig. 8 Effects of height-diameter ratio on accumulated specific energy under different striking velocities

由图8可见，弹速8.5 m/s时，随着高径比增加，B1，M1，H1试样对应累积比能量拟合斜率逐渐减小，M1试样较B1试样的累积比能量增幅减小了32%，H1试样较M1试样则减小了23%；当弹速为9.9 m/s时，M2试样较B2试样的累积比能量上升幅度减小了64%，H2试样较M2试样则减小了26%，表明在同一弹速条件下，随着高径比增加，累积比能量上升趋势缓慢。这是由于单位体积试样破裂面表面积随着冲击次数增加而增大，应变能随之增长[14]。随着高径比增加，岩样平均应变率整体降低，冲击过程中仅产生少量的破裂面和更大的碎块，从而导致了试样破裂面表面积增加变慢，此时应变能增长幅度逐渐减弱，试样累积比能量上升趋势也随之减小，体现出外部能量对岩石作用是造成岩石内部损伤的直接原因。此外，还发现当高径比变化时，岩样的能量耗散特性对循环次数的敏感程度不同，B组试样对循环次数的敏感性最强，累积比能量吸收值增长幅度最大。可见，岩石破坏过程中的能量耗散特性与其内部损伤有十分密切联系，通过对弹性模量与吸能耗能特性的分析，能够深化对循环冲击过程中岩石损伤演化的理解和认识。

图8还显示同一弹速下，试样累积比能量随冲击次数的增加而增加。这是因为在循环冲击过程中，试样每次冲击下都要吸收入射波能量，单位体积试样的吸收值以弹性势能的形式储存在试样内部，导致了试样内部更多微裂纹的孕育与起裂。一旦弹性势能累积达到储存能量阈值，试样内部的弹性势能得到释放，以耗散能形式作用于试样损伤破坏上，表现为更多的微裂纹发生扩展、贯通，从而导致破碎面增加，单位体积试样破裂面表面积增大，应变能相应增加，故累积比能量有所增加。

2.6 岩样破坏模式比较

图9和10分别为两组弹速下3种高径比花岗岩试样的破坏形态。低弹速下（如8.5 m/s），随着高径比增加，试样的破碎块度增大、破碎块数减少；此外，试样出现纵向贯通裂纹，呈现轴向劈裂破坏模式，这是由于随着高径比增加，试样平均应变率整体减小。在低应变率下，只有少数微裂纹被激活，它们沿着压应力方向扩展，相互贯通，形成平行于加载方向的纵向贯通裂纹，最终导致试样呈现轴向劈裂破坏模式。高弹速（如9.9 m/s）下，随着高径比增加，试样破碎程度降低，由轴向劈裂转变为边缘仅少量剥落。这是因为岩样内部损伤较小，形成了少量破裂面及碎块，从而导致比表面积增加幅度减小，累积比能量上升趋势变慢，宏观上表现为试样破碎程度渐弱。