医用3D 打印批次智能排样研究
2020-05-12李方娟赵玉佳赵君嫦孟祥丽郭强孟繁钦
李方娟,赵玉佳,赵君嫦,孟祥丽,郭强,孟繁钦
(1.牡丹江医学院药学院;2.牡丹江医学院红旗医院,黑龙江 牡丹江 157011)
3D 打印是一种快速成型技术,采用数字技术材料打印机来实现的,运用粉末状金属或其它可黏合材料,通过逐层打印的方式来构造物体的技术。最近几年,3D 打印技术在医学各个领域得到了广泛的应用,3D 打印肝脏模型、头盖骨、脊椎植入体等;3D 打印除具有个性化定制要求外,对于3D 打印医用传感器、助听器外壳、康复医疗器械等具有批量打印要求。在批量3D打印加工中,当同时打印多个工件时,为提高工件的打印效率,通常将多个零件排布于打印机台面内同时打印,即一个打印批次可以同时加工出多个零件,如一个批次无法完成全部零件的打印,就需要安排多个打印批次进行打印。因此,对打印工件进行合理的排样,对缩短打印时间、提高3D 打印加工效率至关重要。3D 打印工件排样问题是一个复杂的多约束优化问题,本文提出采用CHNN 神经网络算法进行3D 打印排样,并结合遗传算法优化神经网络,通过算法实现,完成了3D 打印批次排样问题的研究。
1 排样问题的求解
1.1 排样问题数学模型建立
在批量3D 打印过程中,每个打印批次通常排布多个零件,又由于3D 打印是沿着零件的高度方向逐层进行打印的,因此,要想提高整个打印批次零件的加工效率,对打印零件进行合理的规划排样至关重要。由于3D 打印是逐层进行打印的,在同一批次工件打印中,打印时间是以高度最大的零件完成打印进行计算的。因此,要想提高整个批次打印零件的效率,必须保证同一打印批次内打印零件的高度差最小。设第Q 个打印批次内有n 个零件进行打印,各个零件的高度分别为h1,h2,…,hj,…,hn,其中打印零件件的最大高度为hmax,要使零件打印所需时间最短,应该满足如下条件:

1.2 CHNN 用于排样问题算法设计
连续型Hopfield(CHNN)神经网络是1982 年由美国物理学家霍普菲尔德教授提出的一种单层反馈神经网络。CHNN 神经网络求解组合优化问题,就是在给定约束条件下,求出使目标函数极小(或极大)的变量组合问题。将排样问题映射到CHNN 人工神经网络:首先把排样问题映射到一组神经网络的特定组态上,此组态相应于排样问题的可能解,然后构造一个适合于优化问题的能量函数E,此E 正比于优化问题的评价函数。所选的评价函数的好坏直接影响排样的效率和结果。为了保证排样结果的有效性,排样问题的求解需要满足如下条件:假定有P 个3D 打印零件,将其分成Q 组(即Q 个打印批次),则网络使用PXQ 个神经元,将这些神经元按照P 行Q 列排列。当网络达到稳定状态时,上述神经网络的求解问题必须满足一定的约束条件。在满足约束的条件下,优化排样问题与约束之间的对应关系如表1 所示。
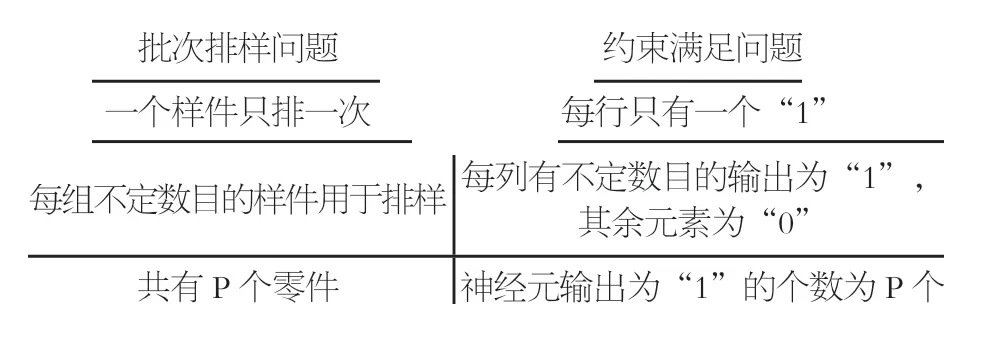
表1 排样问题满足的约束条件
3D 打印排样问题的能量函数如下:
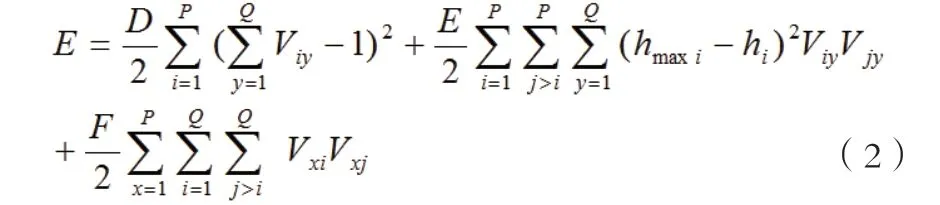
式中,D、E、F 为正系数; hmaxi为每组中排样件的最大高度; hi为排样件的高度;为第X 行第I 列的神经元输出即排样对象被分到标号为x 的组中。
其神经元之间的权值如下:
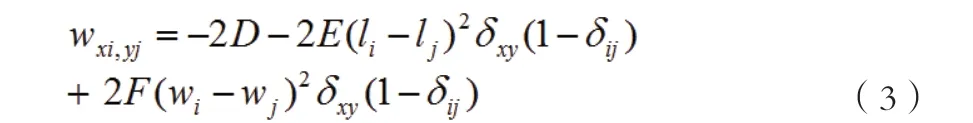
式中:
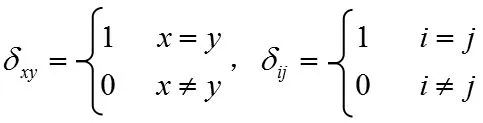
1.3 遗传算法优化CHNN 神经网络
遗传算法是一种通过模拟自然进化过程搜索最优解的方法,通过复制、交叉、变异将问题解编码表示的“染色体”群进行迭代进化,从而得到问题的近似最优解。将神经网络中所有的神经元的连接权值编码成二进制码串或实数码串表示的个体,随机生成这些码串的初始群体进行遗传算法的计算。每完成一次迭代计算后,将码串解码为权值构成新的神经网络,通过对所有训练样本进行计算得到神经网络输出的均方误差从而确定每个个体适应度。经过若干代的计算,神经网络将进化到误差全局最小。
其求解过程如图1。

图1 遗传算法优化神经网络流程
2 排样问题实例验证
将用遗传算法优化的CHNN 神经网络使用MATLAB 语言进行程序的实现。以20 个3D 打印零件的加工为例进行验证,3D 打印零件的数量和相应尺寸如表2 所示。
排样结果在输出前建立如下规则:以被打印零件在水平面投影的最小包络矩形作为输出值,将打印工件在三维空间的排布问题转化为二维图形的输出。打印图形输出结果如图2 所示。
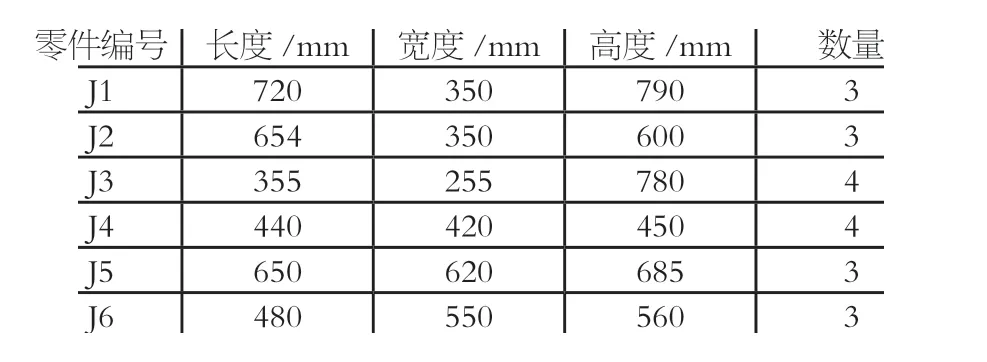
表2 排样零件参数表

图2 3D 打印图形的二维输出
3 结语
本文采用CHNN 神经网络和遗传算法结合解决3D 打印工件批次排样问题,通过将排样问题的目标函数映射到CHNN 神经网络,建立了神经网络的能量函数并完成了算法的程序实现,很好的解决了多约束的组合优化排样问题,提高了3D 打印工件的加工效率。
