基于人工智能方法的电力系统动态等值的应用研究
2020-05-11宋才华邓乾
宋才华 邓乾
摘 要: 电力系统中,动态等值分析方法越来越得到重视,它具有简化系统的运算过程、提高运算能力等特点。介绍几种等值方法并简要的分析了各自特点,阐述了电力系统建模的原理和建立模型的主要类别,提出了A模型的设计方案并对其建立和测试过程作了论述。
关键词: 电力系统; 动态等值; 人工智能
中图分类号: TP311 文献标志码: A
Analyss of Dynamc Equvalence of Power System Based on Artfcal ntellgence
SONG Cahua, DENG Qan
(Foshan Power Supply Bureau, Foshan 528000)
Abstract: n the power system, the dynamc equvalence analyss method s gettng more and more attenton. t has the characterstcs of smplfyng the operaton process and mprovng the computng power of the system. n ths paper, several equvalent methods are ntroduced and ther characterstcs are brefly analyzed. The prncples of the modelng of power system and the man categores of the model are expounded. The desgn scheme of the A model s put forward and the process of ts establshment and testng s dscussed.
Key words: Power system; Dynamc equvalence; Artfcal ntellgence
0 引言
随着经济的迅速发展,电力系统也正迅速向多机、大电网、交直流混合输电及大区域电网互联运行的趋势发展,这样使得电力系统离线分析在仿真计算的维度和复杂度上都面临着很大的困难,对于在线分析如EMS(Energy Management System)等在速度和精度上更是提出了更高的要求[1]。因此对系统进行必要的简化,是十分必要也是十分迫切的。
随着针对目前电力系统的规模不断扩大,动态等值作为一种系统简化的方法,具有可以大大降低计算量、降低方程的维数并能保持系统主要特征等优点,对于实时在线分析十分重要,受到了越来越多的重视[2]。
1 等值方法分类
1.1 同调等值法
同调(coherency-based)等值法是一种基于发电机同调概念的等值方法,将满足同调条件的发电机等值成一台发电机。同调等值法主要适用于电力系统离线大扰动下的暂态稳定分析[3]。
同调等值法的优点:物理透明度大,可直接用于暂态稳定分析,适应系统的非线性和大扰动,且可以适用于大规模系统等值,速度很快,动态等值精度控制较方便等[4]。
同调等值法存在的缺点:同调机群的划分和扰动的地点、类型等因素有关;网络化简、移相变压器的消去会对动态过程带来一定误差;另外,同调发电机聚合较复杂,且有一定拟合误差等[5]。
同调等值法己在电力系统中广泛应用,发展已经比较成熟,很多仿真软件中均有同调等值的功能[l]。
1.2 模式等值法
模式等值法是一种基于外部系统线性化模型和特征值性质进行降阶的等值简化方法,是将外部系统线性化后,根据特征值分析,将频率较高、衰减较快那些特征根对应的模式忽略不计,保留对研究系统影响较大的特征根对应的模式,从而可以对系统进行降阶简化处理。主要用于离线的小干扰稳定分析,有时也可用于离线的大扰动暂态分析,要求等值前后研究系统在小干扰下的主要动态特性(主特征根及相应的主特征向量)基本保持一致[6]。
模式等值法的优点:物理概念明确,可对外部系统作高度简化并保留其主要特征值;一旦获得了有关外部系统的动态等值,就可用同一等值模型对研究系统内的大量故障进行计算分析,只要故障不发生在太靠近等值的边界即可[7]。
模式等值法的缺点:主要在等值过程中要形成外部系统的线性化模型,通过系数矩阵作特征根分析,当外部系统极大时,求特征根会有“维数灾”问题,等值计算工作量较大。可以将外部系统分为若干外部区域,对每个外部区域采用上述方法,则“维数灾”的问题基本可解决。另外,等值后的外部系统用线性化方程表示,若用于暂态稳定分析,则要对常规程序作修改[8]。
1.3 估计等值法
估计等值法实际上根据量测量(或者外部系统的动态响应)来估计和辨识外部系统及其等值模型参数的方法。目前在线用的估计等值法根据扰动的不同可分为两大类:一类利用人为的确定性扰动,记录系統响应,由此估计外部系统的等值参数;另一类是利用随机扰动,记录系统的响应,经过滤波及信息处理,获得等值系统的参数估计[7]。
前者抗干扰性能好,人为扰动有一定强度,但不太实用,因为要施加确定性扰动,影响系统运行,一般采用最小二乘估计方法。后者要求作必要的滤波及相关分析,以防止噪声干扰,数学处理较复杂,但较适应于实际应用要求,它一般采用极大似然函数和卡尔曼滤波的估计方法[9],即把在线量测值减去预估量的残差的似然函数重复地进行最小化,直至最优。
与同调法和模式法不同,估计等值法不需要外部系统的详细数据,能够适应系统的工况多变和结构多变,适用于大规模电力系统的在线安全分析。在电力市场化的新环境下,各电力公司为了追求利益最大化,相互之间的数据具有不透明性[10]。因此,在电力市场的环境和实时在线的要求下,研究估计等值法是一个很有实际应用意义的工作,估计等值法的发展将会是电力系统仿真发展不可避免的趋势,是实现大电网在线安全分析的前提。
2 系统模型和辨识理论
2.1 模型概述
模型就是把实际的物体中的本质部分用直观的信息形式进行表达。常用的模型可分为物理模型和数学模型两大类。物理模型是根据相似原理构成的一种物理模拟;数学模型是指以数学表达式来描述过程的动态特征,在时域上常用的形式有代数方程、微分方程、差分方程、状态方程等。两种模型的形式不同,其研究的方式也相异。物理模型通常通过模型试验来达到动态特性的研究;而数学模型则需通过数字仿真计算来阐述动态过程[11]。
在电力系统中随着规模的不断扩大和计算技术的不断发展,物理仿真已经越来越不能满足要求,采用数学仿真进行动态计算也越来越显示出其优越性。
2.2 辨识的基本原理
辨识实际上就是一种建模的过程,利用被控制系统的输入和输出,通过一定的数据处理,估计出被控制系统的数学模型[12]。随着电力系统间的互联,系统的规模不断扩大,人们对于电力系统精确仿真越来越重视。
动态等值作为简化现代大规模电力系统的一种手段,在大规模系统仿真和实时在线动态安全分析方面都有着十分重要的意义。对仿真的精确度愈来愈高,也就要求动态等值所保留的等值精度越来越高,因此对于动态等值采用的模型的精度要求更高[13]。
2.3 电力系统的元件模型
电力系统仿真是电力系统进行设计、规划、运行等的主要工具,相应的决策无一不是以仿真计算结果为依据。如果相应的决策基于偏保守的仿真结果,则会造成不必要的浪费;如果相应的决策基于偏乐观的仿真结果,则会给系统构成潜在的危险[14]。因此对于电力系统仿真的元件数学模型进行详细的研究,再结合研究的需要,恰当地选取元件模型时十分重要的,同样对于动态等值,尤其是估计等值方法,确立外部系统的元件模型是十分关键的。
3 人工智能及模型设计方案
3.1 人工智能方法
人工智能方法是一种借鉴和利用自然界中自然现象或生物体地各种原理和机理而开发并具有自适应环境能力的优化方法。
进化算法的发展,使得经典人工智能算法的研究再度掀起,使得人工智能算法成为当今研究的热点,并已发展成为一种多学科、多智能交叉融会、渗透的信息与计算研究领域。经典人工智能方法与来自生命科学中的其他生物理论相结合,使得这类算法有了较大的进展,神经网络与免疫网络的结合成了免疫神经网络。现代人工智能方法在经典的人工智能方法的理论及应用基础上,已逐步发展出许多较有潜力的分支。人工智能方法已经呈现出了较多的工具,如免疫遗传算法、混沌免疫算法、蚁群优化算法等,这些都显示了模拟或者借鉴生物智能[15]。
目前人工智能方法呈现出三大发展趋势:一是对经典智能算法的改进和广泛应用,以及对其理论的深入、广泛研究;二是现代智能算法的发展,开发新的智能工具,拓宽其应用领域,并寻求理论基础;三是经典人工智能算法与现代人工智能算法的结合建立混合智能算法[16]。
3.2 A模型设计方案
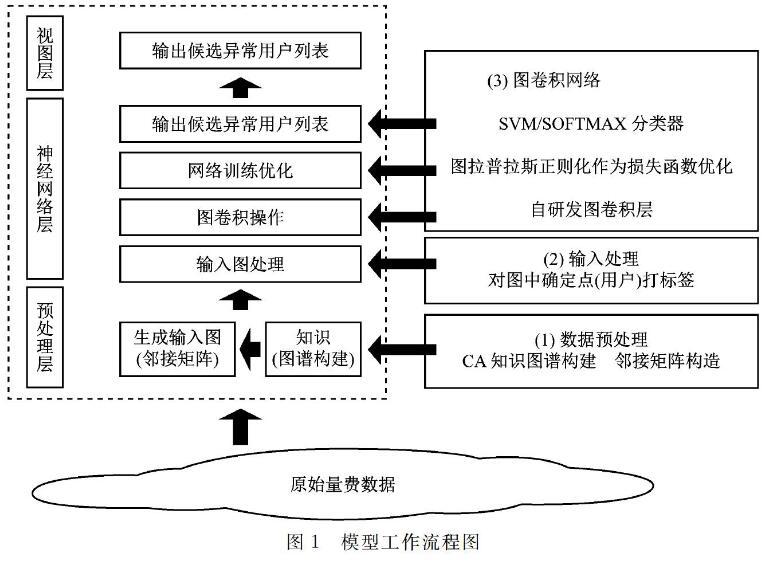
根据原始数据构建量费领域知识图谱,然后根据此知识图谱基于神经网络做一系列操作,包括知识图谱的表示学习,卷积编码操作学习数据的特征等,并基于这些特征输出候选异常用户。模型工作流程设计方案如图1所示。
4 A模型建立及测试
根据原始数据构建量费领域知识图谱,然后根据此知识图谱基于神经网络做一系列操作,包括知识图谱的表示学习,卷积编码操作学习数据的特征等,并基于这些特征输出候选异常用户。
4.1 模型的建立
模型输入主要步骤如下。
(1) 梳理原始“量费”业务稽查相关数据,建立完整“量费”稽查业务语义体系,利用上述语义体系构建基于CA模型(Core-Attachment)的知识图谱,接着设定需求自适应规则/参数对用户点相连方式,生成邻接矩阵输入图,保证模型的通用性。
(2) 通过构建一个多层级结构的图模型,考虑主次级别的基础上建立不同对象之间的关系,更加准确的度量对象之间的相关性。
(3) 采用一种基于卷积神经网络的表示学习算法,实现针对知识图谱的卷积神经网络编码器,同时结合循环神经网络,建立一个一个混合模型以弥补卷积神经网络的不足,同时使用动量随机梯度下降对模型进行优化。
4.2 模型测试
(1) 充分利用半监督学习算法,对输入图的部分用户进行语义标注,有效降低人工标注工作量;在神经网络层,研发高效可按需调整、支持扩展操作的图卷积层作为图卷积网络的隐藏层。
(2) 使用整流线性单位(ReLu)作为激活函数以及图拉普拉斯正则化作为损失函数对网络进行训练优化。
(3) 根据实际问题是二类还是多类,采用决策向量机(SVM)或者SOFTMAX函数对输出结果进行最终分类并打上对应标签。
4.3 模型输出
首先选择合适的分类算法,用单一的算法对电力数据进行处理,选择获得最佳结果的前N个算法。
在選定一组基于全局准确率的最佳方法后,设计一个集成深度学习模型进行多分类器融合学习。
针对模型中特征重要性测量问题,采取传统集成学习算法与循环神经网络特征学习信息结合的方式进行特征重要性赋值。
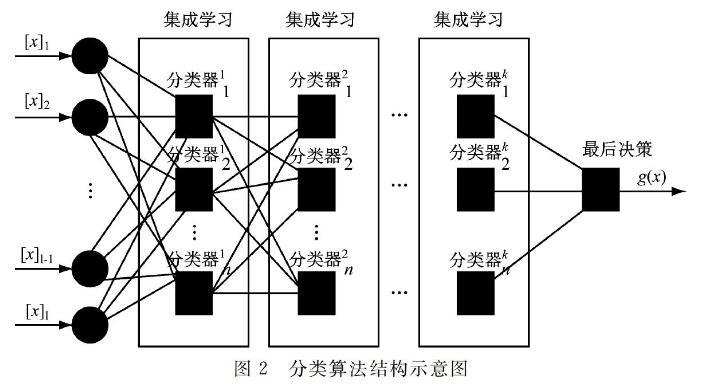
结合多个重要性指标如本地正确率、多样化正确率、局部泛化误差界等进行每层分类器的权重计算,完成集成学习模型的构建。分类算法结构示意如图2所示。
4.4 模型效果
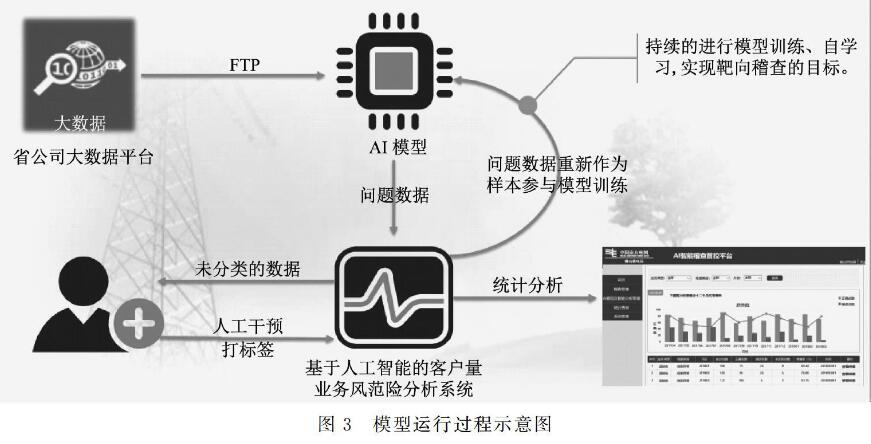
模型应用,可以定向有重点地对数据进行处理,很大程度上提高了整个运算系统的效率;对数据处理进行人工干预,有效地避免过程中运算错误带来的问题,能够及时纠正问题。模型运行过程如图3所示。
5 总结
针对目前电力系统的规模不断扩大,对于实时在线分析的要求越来越高,本文对电力系统的动态等值方法进行了研究,提出了一种A模型的解决方法。针对电力系统动态等值过程中的研究,得到的结论如下:
(1) 对目前电力系统的三大动态等值方法:同调等值法、模式等值法和估计等值法。同调等值法和模式等值已经应用较多,估计等值法在未来将会有所突破和发展。
(2) 人工智能方法与其他优化算法相比,具有精度高、速度快、收敛性好、鲁棒性强的优点,因此适合于动态等值算法。
(3) 本文提出的A模型算法可以对大数据平台进行分析,并可以对问题数据进行再分析及人工干预、矫正分析过程,使样本数据分结果更加精确。
参考文献
[1] 吴敏玲.基于运行数据的风电场动态等值建模及故障预警研究[D].泉州:华侨大学,2017.
[2] 华玉婷,李生虎. 基于SMP状态空间等值的智能变电站保护系统短期可靠性评估[J].系统工程理论与实践,2016,36(9):2439-2448.
[3] 晁璞璞,李卫星,金小明.关于双馈风电场动态等值的认识和探讨[J].电力系统自动化,2016,40(12):194-199.
[4] 廖庭坚,刘光晔,雷强,等.计及电动机负荷的电力系统动态等值分析[J].电网技术,2016,40(5):1442-1446.
[5] 张星,李龙源,胡晓波,等.基于风电机组输出时间序列数据分群的风电场动态等值[J].电网技术,2015,39(10):2787-2793.
[6] 崔晓丹,李威,李兆伟,等.适用于机电暂态仿真的大型光伏电站在线动态等值方法[J].电力系统自动化,2015,39(12):21-26.
[7] 曹晏莱.基于灵敏度分析的中小水电机群动态等值方法研究[D].武汉:华中科技大学,2015.
[8] 罗坚强.基于电网等值的最优励磁控制器设计[D].武汉:华中科技大学,2015.
[9] 周明,葛江北,李庚银.基于云模型的DFG型风电场动态电压等值方法[J].中国电机工程学报,2015,35(5):1097-1105.
[10] 潘学萍,张弛,鞠平,等.风电场同调动态等值研究[J].电网技术,2015,39(3):621-627.
[11] 高远,金宇清,鞠平,等.考虑Crowbar动作特性的DFG风电场动态等值研究[J].电网技术,2015,39(3):628-633.
[12] 王增平,张乐丰.考虑弃风的DFG风电场动态等值模型[J].电力系统保护与控制,2014,42(13):1-6.
[13] 朱良合,栾会,毛承雄,等. 基于电网动态等值的PSS参数智能优化方法[J].广东电力,2014,27(3):28-33.
[14] 邓桂秀.基于人工智能算法的配网重构和拓扑分析的研究[D].福州:福州大学,2014.
[15] 栾会.基于电网动态等值的PSS参數优化[D].武汉:华中科技大学,2014.
[16] 李静.智能变电站全场景试验系统仿真与测试软件平台研制[D].成都:电子科技大学,2012.
(收稿日期: 2018.11.14)
作者简介:宋才华(1976-),男,湛江市,研究方向:供电系统客户服务的信息化建设与应用。
邓乾(1993-),男,佛山市,研究方向:供电系统客户服务的信息化建设与应用。文章编号:1007-757X(2020)01-0134-04
