基于优化最大偏差相似性准则的KNN缺失数据填充算法*

阮嘉琨 蔡延光 蔡颢 王建成

基于优化最大偏差相似性准则的KNN缺失数据填充算法*

阮嘉琨1蔡延光1蔡颢2王建成1

（1.广东工业大学自动化学院，广东 广州 510006 2.奥尔堡大学健康科学与工程系，丹麦 奥尔堡 9920）

根据高速公路交通数据的特点，采用基于最大偏差相似性准则（MDSC）与KNN填充算法对缺失交通数据进行填充。针对KNN填充算法可能产生伪邻近点问题，提出利用MDSC对不完整的交通数据中缺失的属性样本和完整值数据样本进行聚类，以避免伪邻近点发生；并利用基于骨干粒子群算法对MDSC参数优化。实验结果表明：基于优化MDSC的KNN填充算法的值更小，效果更优。

智能交通；高速公路；缺失数据填充；聚类算法

0 引言

缺失值是指在特定时间未按计划从特定主体获得特定变量的情况[1]。由于高速公路上检测仪器硬件损坏或软件运行错误等原因，高速公路交通数据出现缺失值的情况较常见。部分数据缺失会影响数据分析结果，导致无法对高速公路的实际交通情况进行合理分析处理，从而难以准确预测及报警。因此，缺失值填充对高速公路交通数据优化至关重要。

缺失值填充方法主要有人工填充、特殊值填充、平均值填充、热卡填充、回归模型填充、期望值最大化法、多重填补和-最近邻（KNN）填充算法等。Dixon等[2]提出了KNN填充方法，先利用KNN计算邻近的个数据；然后填充它们的均值。Jhun M等[1]提出一种基于自适应最近邻（ANN）的填充方法，该方法考虑了数据的局部特征，可根据缺失值的位置调整邻居数量。Park[2]等人提出一种顺序自适应最近邻（SANN）填充方法，该方法在选择缺失观测值的最近邻居时，将缺失观测值的局部特征考虑在内，且以顺序方式重新使用估算的观测值。Kim等[3]采用基于支持向量机回归模型测试缺失数据填充方法的效果，实验结果表明：KNN填充算法处理后的数据与原始数据最接近，且即使丢失数据速率增加，预测模型性能也较稳定。

考虑到高速公路交通数据量庞大，数据特性复杂、计算繁琐，本文采用KNN填充算法对高速公路交通缺失数据进行填补。为避免出现最邻近噪点情况而使KNN填充算法准确率下降，本文提出一种基于最大偏差相似性准则（maximum deviation similarity criterion, MDSC）[4]的KNN填充算法，即交通数据样本集先采用MDSC进行聚类；再利用KNN填充算法对缺失数据所属的聚类簇进行填充。

1 基于骨干粒子群算法的优化MDSC

1.1 MDSC

每条高速公路的交通数据都有时间维度的相似性，本文采用的MDSC根据交通数据间的差异程度进行算法聚类。高速公路交通数据通常符合时间规律，但受天气、交通事故和施工等影响会出现异常数据。虽然异常数据较少，但若忽略这些数据，会使缺失数据填充的准确率下降。为此，本文提出优化的MDSC，即对最后输出聚类簇包含的数据曲线设置阈值，低于阈值的聚类簇被当作异常数据曲线过滤掉。

MDSC步骤：

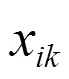
1.2 骨干粒子群算法

Kennedy于2003年提出了骨干粒子群算法[5]。与标准粒子群相比，其去掉了速度、加速系数和权重等参数，且粒子位置更新由高斯分布获取，算法更简洁，参数更易调整。位置更新公式为

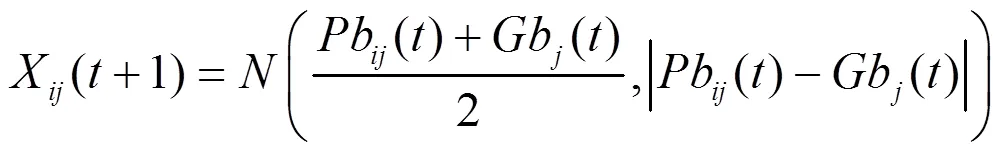
高斯骨干粒子群算法步骤：

2）根据式(2)更新骨干粒子群中个体位置；

3）根据式(3)判断粒子个体是否有越界行为，若有则重新初始化，相反执行步骤4）；

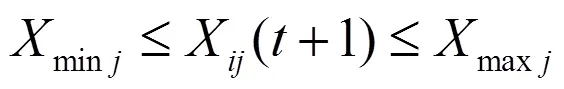
4）重新计算全部粒子个体的适应度值(X)；

5）由式(4)更新所有粒子个体，并将粒子群全局历史最优位置赋给；

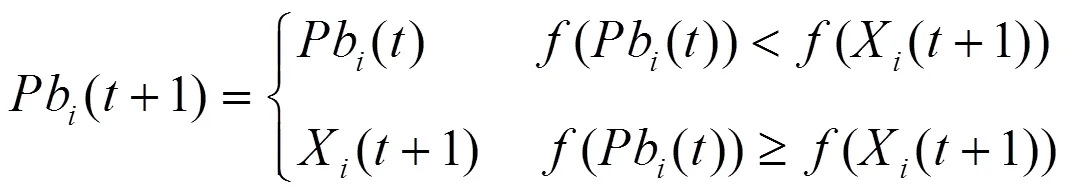
6）判断是否达到终止条件，若达到则输出最优粒子位置，相反则跳转到步骤2）。

1.3 优化算法设计

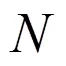
3）更新粒子群中每个个体位置，并判断骨干粒子个体是否有越界行为；

4）重新计算全部粒子个体的适应度值(X)，并更新个体的最优位置及全局的最优位置；

6）将最优粒子解赋给参数(,,)，执行最大偏差相似性聚类，输出聚类结果。

2 基于优化MDSC的KNN填充算法设计

2.1 KNN填充算法

KNN填充算法以缺失数据样本点的位置坐标为参考目标，计算数据样本集中所有正常数据样本点与缺失数据样本点的欧式距离d（= 1,2,...,），计算公式如式(5)所示；筛选个最小d值，则这个d值所对应的坐标点即为离缺失数据样本点最近的个正常数据[6-9]；取这些完整数据的加权平均值来代替缺失数据[10]，即可填补数据样本集中缺失的数据，加权值公式如式(6)所示。

其中，为样本空间维度；为维空间中两点间的距离。

填充缺失数据值的公式为

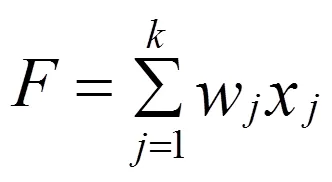
KNN填充算法步骤：

1）从全局整体数据集合中抽取完整的数据创建健全数据集合；

2）计算缺失目标点与健全数据集合中全部个体数据点的欧式距离d；

3）根据欧式距离d大小升序筛选出前个数据点；

4）根据式(6)对这个数据点执行权重计算；

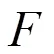
6）判断实验样本集中是否还有缺失数据，若有跳转回步骤2），反之结束，缺失数据填充完毕。

KNN填充算法流程如图1所示。

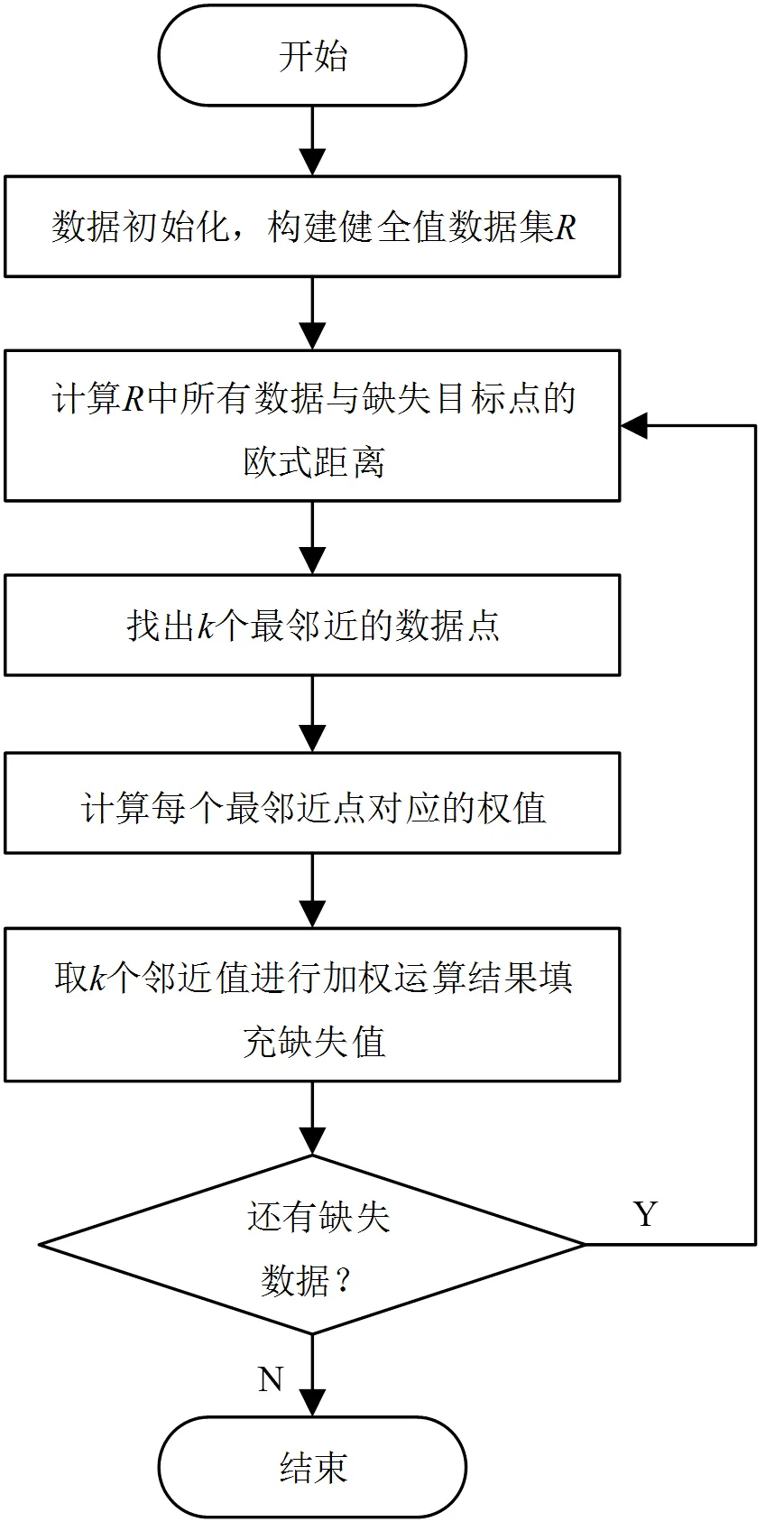
图1 KNN填充算法流程图

2.2 基于优化MDSC的KNN填充算法

通过欧式距离d计算发现，有些属于另一个密集群的数据点比相同密集群的目标点距离更近，这样利用KNN填充算法时会出现伪邻近点，而伪邻近点与个最邻近中其余邻近点没有太大关联，即欧式距离d比较大[11-13]。如图2所示，缺失目标点a的8个最邻近点（a1, a2,a3,a4,a5,a6,a7,a8）中，数据点a7与其余7个邻近点关联稀疏，即a7为a的伪邻近点，也是个最邻近点中的噪点。

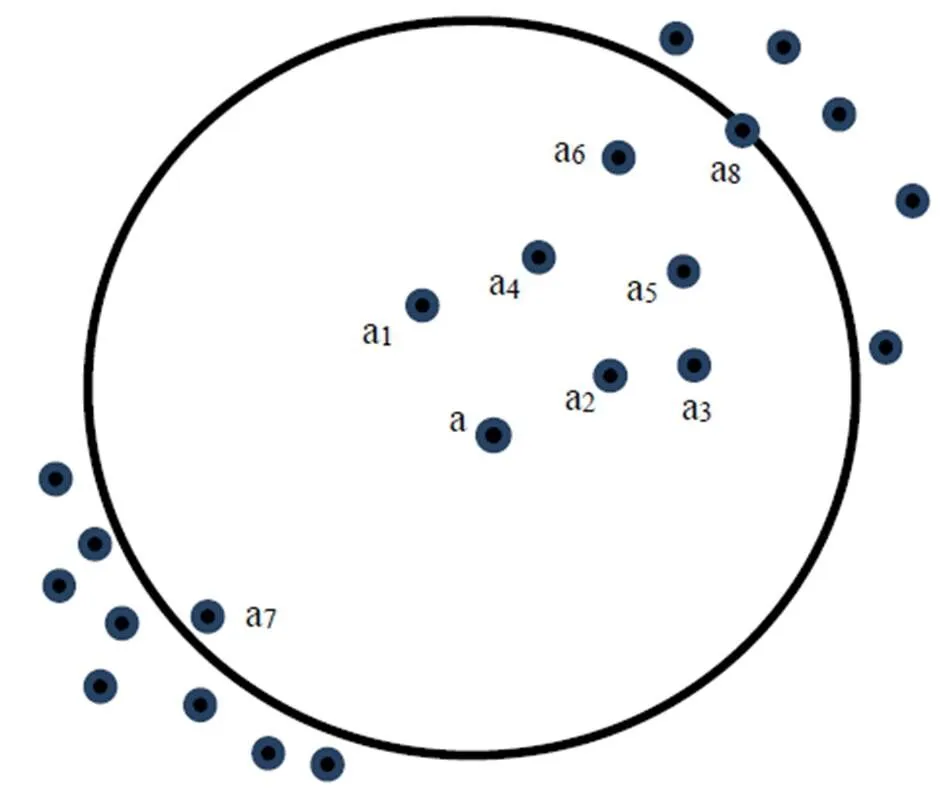
图2 目标数据a的邻近关系图

若直接利用KNN填充算法会使填充结果与实际值之间存在较大误差，影响填充效果[14-16]。为此，本文提出基于MDSC的KNN填充算法，即通过MDSC对总样本数据进行聚类，将关系紧密的相似数据归为同聚类簇；然后再对每一个聚类簇内的缺失目标点运行KNN填充算法，这样能够把不在相同密集群的数据点隔开，从而避免伪邻近点（最邻近噪点）产生。

基于优化MDSC的KNN填充算法步骤：

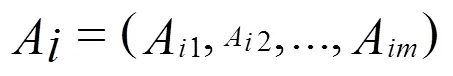
2）将MDSC的参数(,,)作为位置向量，采用骨干粒子群算法得到MDSC重要参数最优解；

3）将最优解赋值给(,,)，利用MDSC对高速公路交通数据集进行聚类，获得聚类划分结果，聚类簇个数为；设阈值= 2，若聚类簇的交通流数据曲线数量小于，则把该聚类簇删除，以此循环判断个聚类簇；

4）由步骤3）过滤异常交通数据后，数据划分为结果的聚类簇，判断缺失交通数据记录在哪个聚类簇，同时在每个缺失数据所对应的聚类簇运行KNN填充算法；

5）对缺失目标对应的聚类簇，根据簇内数据构建完整记录的数据矩阵= (A1,A2,...,A)，设缺失交通数据记录的数量为，缺失目标为a（= 1,2,...,）；

6）计算同一簇内的每个正常数据记录与该缺失目标a的欧式距离d，放到集合中；

7）对欧式距离集合进行排序筛选，选取前个最小的d所对应的高速路交通数据作为缺失目标a的邻近值；

8）根据式(6)计算每个邻近值对应的加权值w（= 1,2,...,），并通过式(7)得到这个值的加权平均值F，即该缺失目标a的填补值a= F；然后令=+1，若﹥执行步骤9），否则返回步骤6），直到该聚类簇内的缺失数据全部被填补；

9）所有聚类簇的缺失数据被填充完，结束算法。

基于优化MDSC的KNN填充算法设计流程图如图3所示。

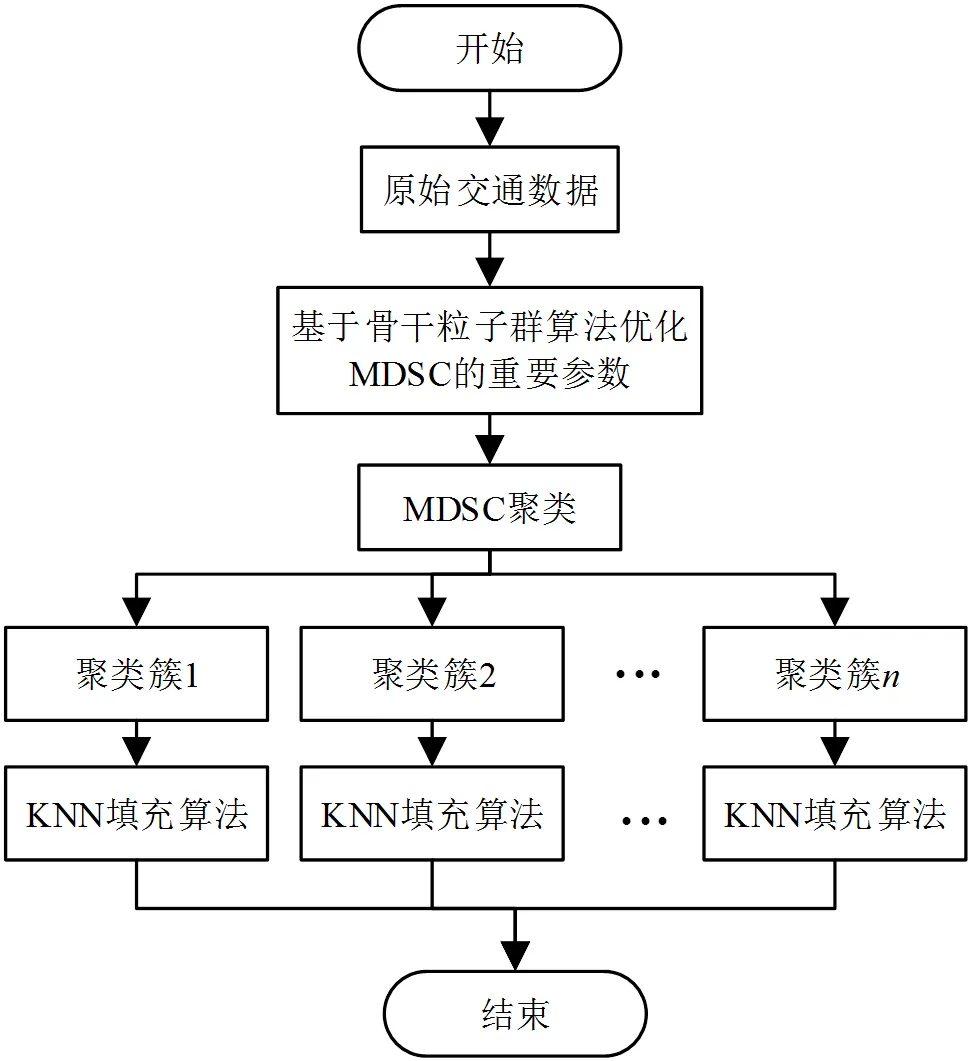
图3 基于优化MDSC的KNN填充算法设计流程图

3 实验与分析

3.1 聚类实验及结果分析

本文以某高速公路2017年8月的交通数据为例，测试优化后MDSC的聚类效果。通过骨干粒子群优化算法得到MDSC聚类对该高速公路交通数据重要参数(,,)的最优解为(0.8, 0.1, 0.15)，MDSC取得较好的聚类效果，如图4所示。

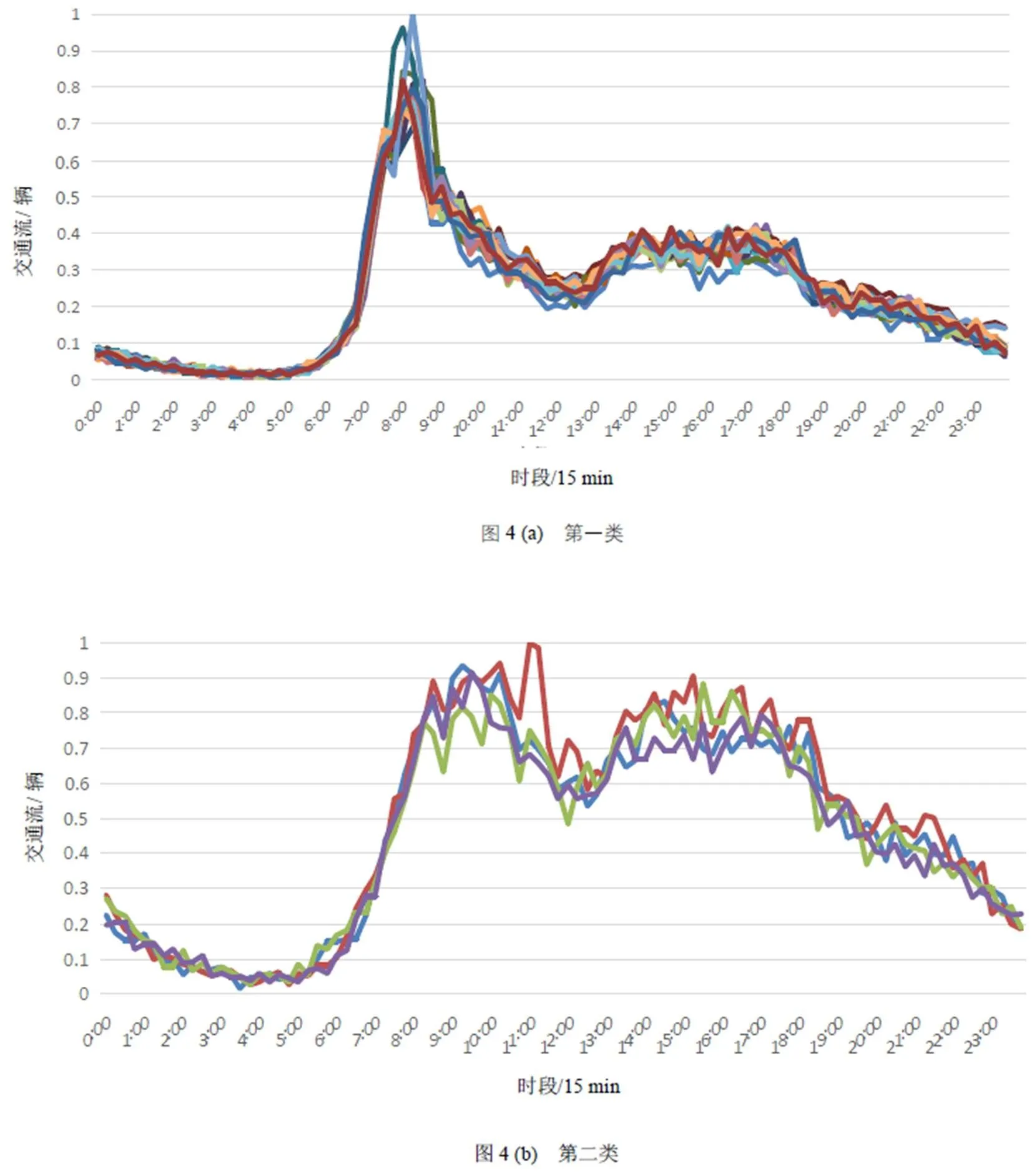
图4(a)中交通流数据曲线波峰和波谷的位置与工作日高速公路早晚交通高峰的时间段是一致的；图4(b)和图4(c)车流量的上升与下降时间与周末大量车辆出行及返程时间基本匹配；在样本交通数据库中核对日期，得出第一、二、三类分别为工作日、星期六和星期天，聚类合理准确，符合实际需求。

为进一步验证优化后MDSC的聚类效果，在高速公路交通数据库中随机抽取一个高速路段的4个月、6个月、8个月、10个月和12个月的交通流数据，对同一数据样本分别执行MDSC算法和基于骨干粒子群优化的MDSC算法进行聚类，各执行10次，利用分类精度进行对比，如图5所示。

图5 2种MDSC算法的分类精度对比图

由图5可知，基于骨干粒子群优化的MDSC算法分类精度有一定程度的提升，且随着交通流数据样本数量增大其精度也提高。

3.2 填充算法结果分析

根据本文提出的基于MDSC的KNN填充算法，对基于MDSC划分数据得到的聚类簇对应的数据记录进行缺失数据填充，并采用（均方根误差）来验证缺失数据填充的效果。计算公式为

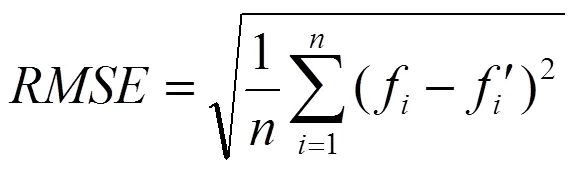
由式(8)可以看出，值越小，填充精度越高。

本文在高速公路交通流数据库抽取的样本数据中随机删除数据，创建缺失比例分别为10%，20%，30%，40%和50%的5组测试样本数据集。实验选取缺失比例为10%的测试样本数据集对不同参数（4, 5, 6, 7, 8）进行测试，填充效果如表1所示。

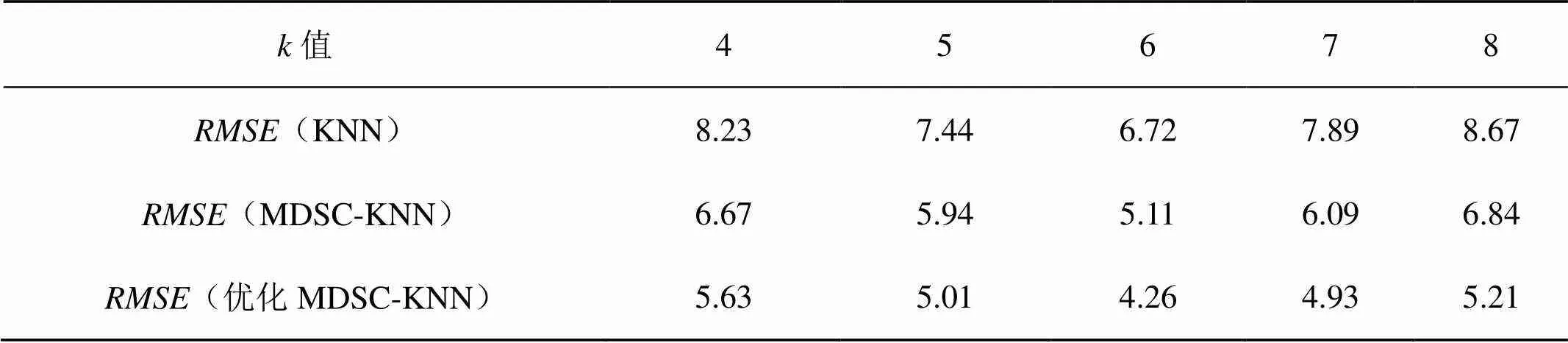
表1 3种算法在不同k值下的填充效果

由表1可知，当= 6时，KNN填充算法与基于MDSC的KNN填充算法的填充效果最好。

为进一步验证填充算法的性能，对缺失比例为10%，20%，30%，40%和50%的高速公路交通流数据样本集分别采用基于优化MDSC的KNN填充算法和传统的KNN填充算法实现缺失交通流数据填充，且2个算法的= 6，实验结果如图6所示。

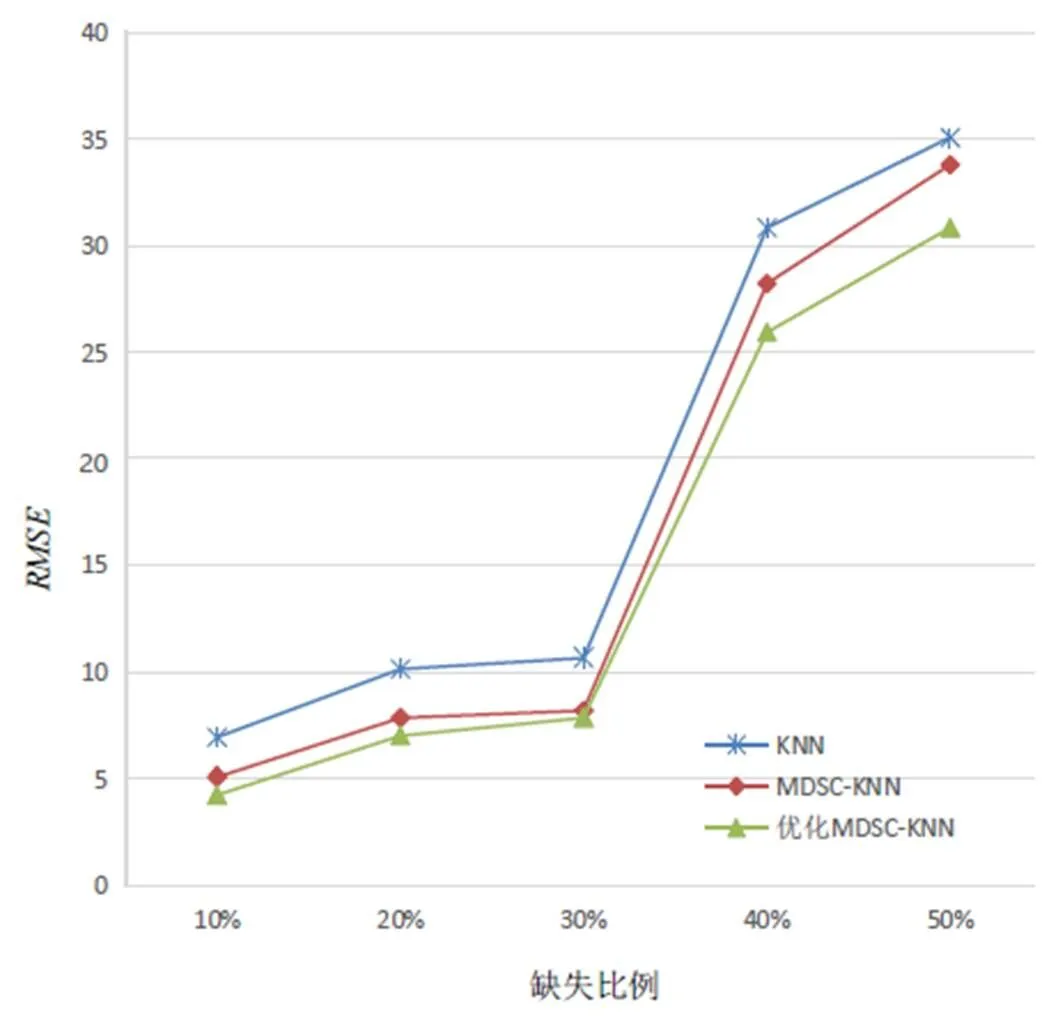
图6 缺失交通流数据填充效果对比图

由图6可知，基于优化MDSC的KNN填充算法的值均小于传统KNN算法的值，且在缺失比例为30%~40%段，值上升最快。总体说，基于优化MDSC的KNN填充算法的缺失数据填补效果明显优于传统KNN填充算法；且相比基于MDSC的KNN填充算法，由于骨干粒子群算法为MDSC寻得最优参数，提高了MDSC的聚类精度，填充效果较好。采用优化MDSC对交通流数据进行聚类，可更准确地找到目标数据点的个最邻近点，填充效果更好。

4　结语

本文采用基于优化MDSC的KNN填充算法对缺失交通流数据进行填充，同时利用基于骨干粒子群算法对MDSC参数寻优。另外针对KNN填充算法可能产生的伪邻近点问题，提出使用优化后的MDSC和不完整的交通数据，对完整值数据样本进行聚类，从而避免伪邻近点的发生。实验结果表明：基于优化MDSC的KNN填充算法相比于KNN填充算法的值更小，鲁棒性更好。

[1] Jhun M, Jeong H C, Koo J Y. On the use of adaptive nearest neighbors for missing value imputation[J]. Communications in Statistics-Simulation and Computation, 2007, 36(6): 1275-1286.

[2] Park, S H, Bang S W, Jhun M S.On the use of sequential adaptive nearest neighbors for missing value imputation[J]. Korean Journal of Applied Statistics. 2011, 24(6): 1249-1257.

[3] Kim T, Ko W, Kim J. Analysis and impact evaluation of missing data imputation in day-ahead PV generation forecasting[J]. Applied Sciences, 2019, 9(1): 204.

[4] 黄何列,蔡延光,蔡颢,等.基于最大偏差相似性准则的交通流聚类算法[J].计算机应用研究,2018,35(08):2274-2276,2292.

[5] Kennedy J. Bare bones particle swarms[C]. Proceedings of the 2003 Swarm Intelligence Symposium. IEEE, 2003: 80-87.

[6] Rezaeian N, Novikova G M. Detecting Near-duplicates in Russian Documents through Using Fingerprint Algorithm Simhash[J]. Procedia Computer Science, 2017, 103: 421-425.

[7] Bai E W, Johnson H, Xu W, et al. A preliminary study on cleaning up erroneous data and filling in missing values in a medical record[J]. IFAC Papers On Line, 2015, 48(20): 493- 498.

[8] Shen J J, Chang C C, Li Y C. Combined association rules for dealing with missing values[J]. Journal of Information Science, 2007, 33(4): 468-480.

[9] Rahman M G, Islam M Z, Fimus. A framework for imputing missing values using co-appearance, correlation and similarity analysis[J]. Knowledge-Based Systems, 2014, 56(1): 311-327.

[10] 袁景凌,钟珞,杨光,等.绿色数据中心不完备能耗大数据填补及分类算法研究[J].计算机学报,2015,38(12):2499-2516.

[11] Rahman M G, Islam M Z. Missing value imputation using a fuzzy clustering-based EM approach[J]. Knowledge & Information Systems, 2016, 46(2): 389-422.

[12] Shahzad W, Rehman Q, Ahmed E. Missing data imputation using genetic algorithm for supervised learning[J]. International Journal of Advanced Computer Science and Applications, 2017, 8(3): 438-445.

[13] Hamza T, Amer A S, Noor A E R. Dynamic L-RNN recovery of missing data in IoMT applications[J]. Future Generation Computer Systems, 2018, 89(12): 575-583.

[14] 李正欣,张凤鸣,王瑛,等.多元时间序列缺失数据填补方法[J].系统工程与电子技术,2018, 40(1):225-230.

[15] 唐良瑞,王瑞杰,吴润泽,等.面向全景调控统一数据模型的缺失数据填补算法[J].电力系统自动化,2017,41(1):25-30, 87.

[16] Jenghara M M, Ebrahimpourkomleh H, Rezaie V, et al. Imputing missing value through ensemble concept based on statistical measures[J]. Knowledge & Information Systems, 2017, 56(1): 123-139.

KNN Missing Data Filling Algorithm Based on Optimized Maximum Deviation Similarity Criterion

Ruan Jiakun1Cai Yanguang1Cai Hao2Wang Jiancheng1

(1.School of Automation, Guangdong University of Technology, Guangzhou 510006, China 2.Department of Health Science and Technology, Aalborg University, Auerbarg 9920, Denmark )

A KNN missing data filling algorithm based on improved maximum deviation similarity criterion is proposed. Considering the characteristics of expressway traffic data, the missing data matching algorithm based on the maximum deviation similarity criterion and KNN is confirmed to fill the missing traffic data. For the problem that the KNN filling algorithm will produce the nearest neighbor noise (pseudo-neighbor), it is proposed to use the maximum deviation similarity criterion to cluster the complete value data samples for the missing attributes in the incomplete traffic data to avoid the pseudo-neighbors. occur. Among them, the key parameter selection problem of MDSC algorithm is based on the backbone particle swarm optimization algorithm to optimize the MDSC parameters. The simulation results show that the missingvalue of the missing traffic data based on the improved MDSC KNN filling algorithm is smaller and the effect is better.

intelligent transportation; highway; missing data filling; clustering algorithm

国家自然科学基金（61074147）；广东省自然科学基金（S2011010005059）；广东省教育部产学研结合项目（2012B091000171，2011B090400460）；广东省科技计划项目（2012B050600028，2014B010118004，2016A050502060），广州市花都区科技计划项目（HD14ZD001），广州市科技计划项目（201604016055），广州市天河区科技计划项目（2018CX005）。

阮嘉琨，男，1993年生，硕士，主要研究方向：大数据质量优化控制、智能交通等。

蔡延光（共同第一作者），男，1963年生，博士，教授，博士生导师，主要研究方向：复杂网络系统建模、控制与优化，智能优化，物联网信息处理与优化控制，大数据管理与分析，智能交通系统。

蔡颢（通信作者），男，1987年生，博士，主要研究方向：大数据分析、智能信息处理等。E-mail: howardbrutii@foxmail.com

王建成，男，1995年生，硕士，主要研究方向：机器学习、数据挖掘等。

TP18

A

1674-2605(2020)02-0002-08

10.3969/j.issn.1674-2605.2020.02.002