泥沙河道管线冲刷的紊动强度及雷诺应力特性实验探究

(乌鲁木齐市水利勘测设计院(有限责任公司)二分院，新疆 石河子 832000)

伴随工程技术和工程材料的进步和发展，时下河道沉管和穿流输运工程日渐增多。掌握穿流管线的沙水冲刷规律特性是该类型工程抗冲刷安全设计、顺利施建和科学维护的基本前提。本文以泥沙河道浅埋穿越管线的冲刷分析为课题，借助实验室比尺模拟实验的方式，对河道管线冲刷的紊动强度及雷诺应力特性进行分析探究，以期为同类工程应用提供技术参考，助力建设和维护安全牢固的穿河管线工程。

1 模型比尺与测量设计

1.1 模型比尺及实验工况

本实验以30mm直径的硬质有机玻璃实心圆管模拟900mm直径的铸铁穿流管线，实验模型的重点水力参数见表1。实验模型、管线及现场状态见图1和图2。

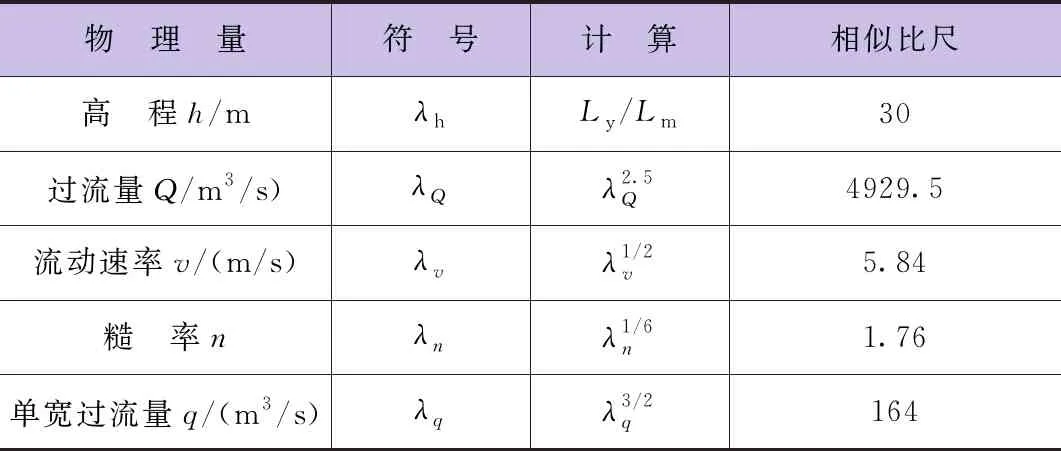
表1 实验模型的重点水力参数

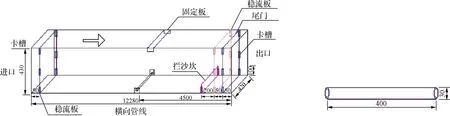
图1 实验模型与管线设计 (单位：mm)

图2 实验模型现场部分图片

实验工况各参数见表2。

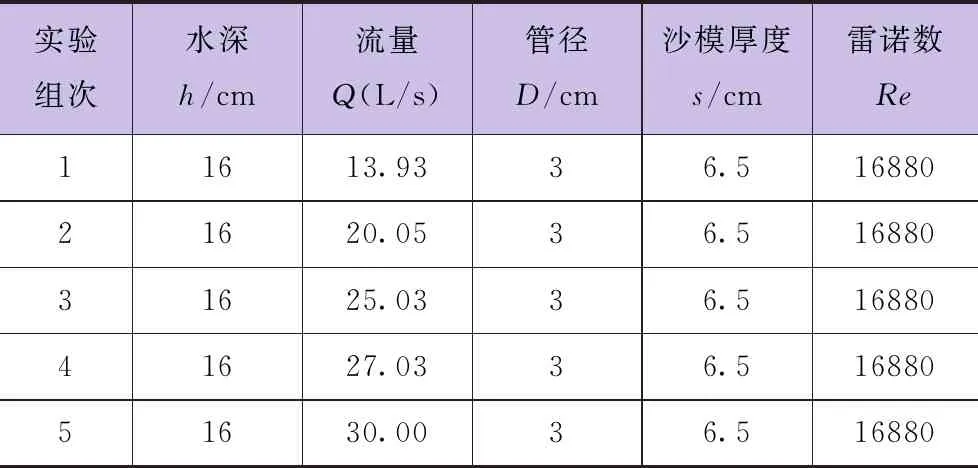
表2 实验工况

1.2 观测截面及测点布设

实验以距玻璃槽底50mm的高度，在透明硬质有机玻璃槽中心部位固定实验所用的30mm直径圆管。考虑管墩桩固定有阻碍水流作用，故选择应用502胶粘贴固定实验管以尽可能降低额外水流扰动。铺设130mm厚模型沙，该沙用水浸润均匀拌和无气泡。调整好模型沙的平整度，误差控制在±3mm内。此时，管上方模型沙厚50mm，管身处模型沙厚30mm，圆管下方模型沙厚50mm，符合以1∶30比例换算后的河底浅埋管线埋置深度需要。模型沙浸水沉淀一夜后，开始实验。

实验的着重点是观测分析模型管线近身周边的冲刷特性，实验前把所制作的两个滑动车衔接在管线四周。在滑动车的下方架子上粘贴软尺，以管线正上方所布设的截面为中心截面，取25mm间距，逆水流向上和顺水流向下各取5个测流截面,即获得顺水流依次为1-1、2-2、3-3、4-4、5-5、6-6、7-7、8-8、9-9、10-10、11-11共计11个测流截面，设置11个测流垂线，分别位处深度30mm、60mm、90mm、120mm、150mm处，每垂线再设置5个测点。距离所测部位30～50mm布置多普勒声学流动速率仪。

2 紊动强度基本特性分析

水流运动存在紊流及层流之分，紊流为绝大多数河道水流存在的一种流态现象。流速脉动是紊流的基本特征，脉动流速有正负大小之分，水流点脉动强度一般用脉动流速均方根表示，称作紊动强度或者脉动强度。本研究选择四个典型截面绘制紊流状态点线图和波动范围云图并重点探讨，以揭示基于过流量差异的沙中浅埋管线冲刷流紊动强度及雷诺应力特性。

实验所需流量由实验水槽进口入流挡板调节控制获得，调节置放在实验水槽尾端出水口的挡板高度，以获得实验所设定流量的相应的流速状态，从而形成多组所设定的实验流量和流速组合工况。本冲刷实验在满足所设定的水深要求后，依据起动流速计算结果，特别拟定了13.93L/s、20.05L/s、25.03L/s 计3种流量工况。

2.1 未冲刷时管线周围紊动强度特性

未冲状态和Q=13.93L/s的紊动强度曲线见图3，不同层基于Q=13.93L/s的紊动强度云图见图4。

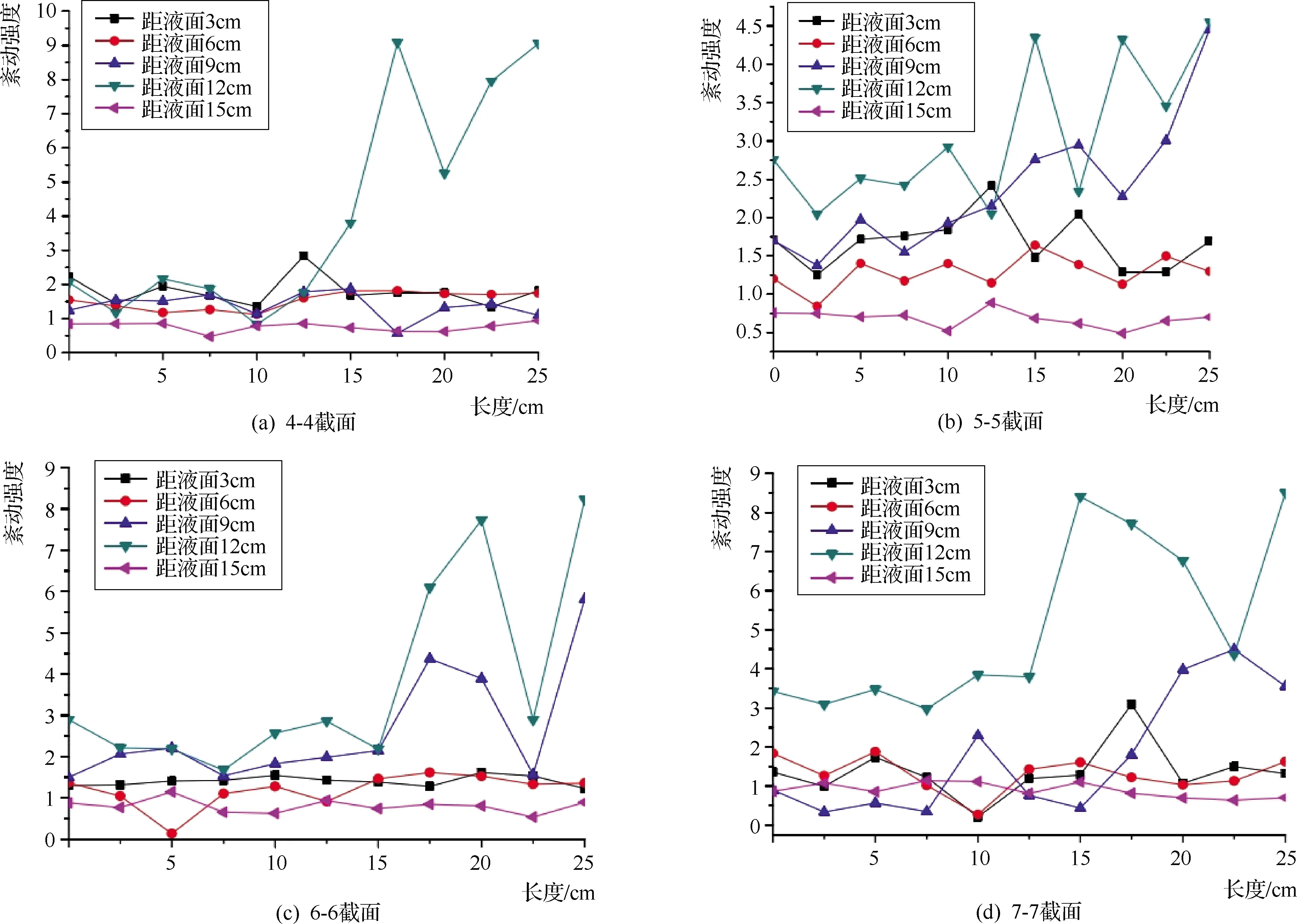
图3 基于未冲状态和Q=13.93L/s的紊动强度曲线

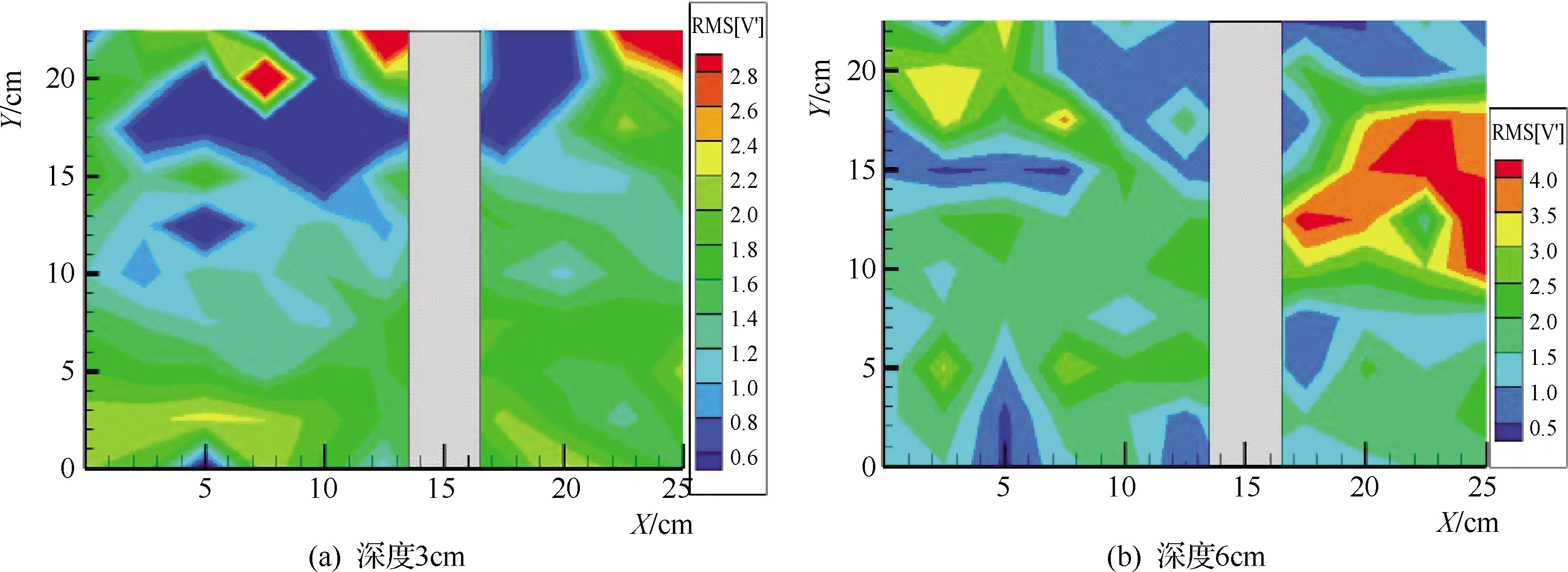
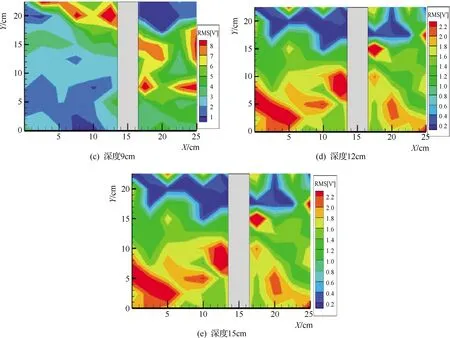
图4 不同层基于Q=13.93L/s的紊动强度云图

由图3和图4可知：因贴近沙面处的水流相对较为平稳，贴近沙面处15cm深度底层的紊动强度波动在0.5～1之间，其平均值约为0.8，没有大的紊动强度改变，是紊动强度相对较小的液层。深度12cm区域的紊动强度在3～6之间变动，其平均值约为4.6。9cm深度区域的平均紊动强度接近2.5。据此可以得到RVS9>RVS6>RVS3>RVS12>RVS15的流动速率规律，其中速率越大的地方，质点交换的能量越大。云图揭示，在未冲状态下，不管是管前还是管后，紊动强度都存在上下浮动，这是由于水流在运动过程中存在能量交换，导致紊动强度在0.5～4之间变动。

2.2 起冲时管线周围紊动强度特性

起冲状态和Q=20.05L/s的紊动强度曲线见图5，不同层基于Q=20.05L/s的紊动强度云图见图6。

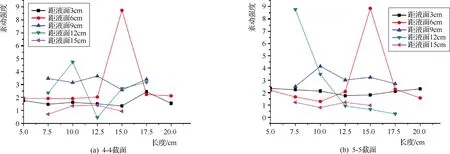
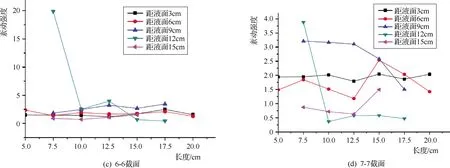
图5 起冲状态和Q=20.05L/s的紊动强度曲线

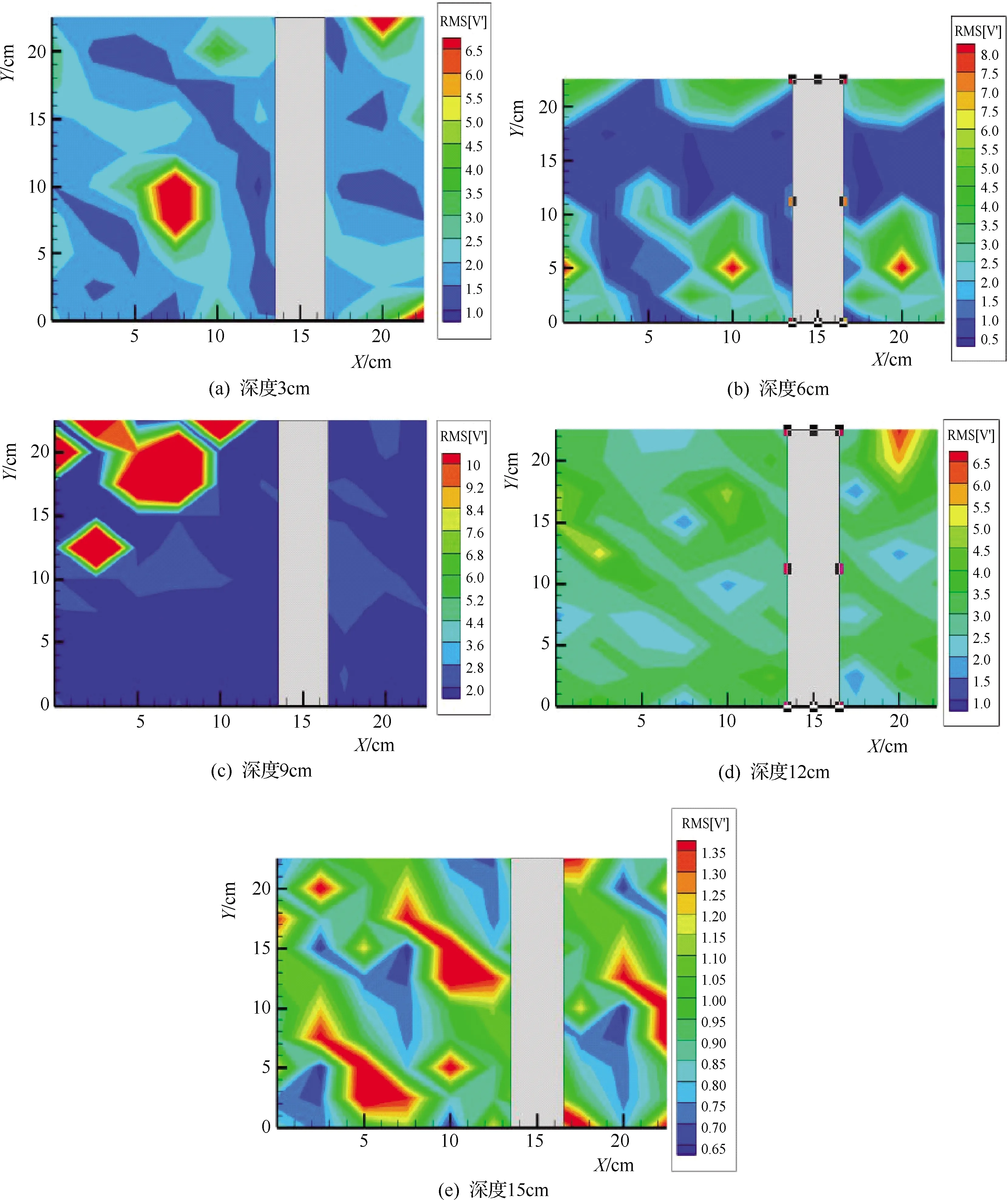
图6 不同层基于Q=20.05L/s的紊动强度云图

由图5和6图可知：ⓐRVS9>RVS6>RVS3>RVS12>RVS15，此与同条件下的纵向流动速率变动特性相同，15cm深度的近底层区域紊动强度相对较小，各工况下管线纵向紊动强度特性演变规律大致相同，在水体中层以上，深度与紊动强度明显呈线性递增关系，与纵向流动速率的演变规律一致；ⓑ近底层紊动强度波动在0.65～1.45之间，是未冲状态强度的1.2倍左右，近面层深度3cm区域的紊动强度基本是左侧低于右侧，模型壁对流动速率存在较大影响，导致质点剧烈交换能量；ⓒ在管线附近存在着一个紊动强度波动的核心区域，紊动强度发生值最大，此时管线对紊动强度的影响范围管后是管径的2.5倍，管前是管径2.0倍。

2.3 冲刷裸露至稳定状态时管线周围紊动强度特性

冲刷到裸露和Q=25.03L/s的紊动强度曲线见图7，不同层基于Q=25.03L/s的紊动强度云图见图8。

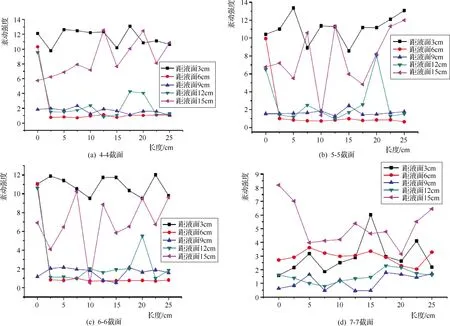
图7 冲刷到裸露和Q=25.03L/s的紊动强度曲线

由图7和图8可知：ⓐRVS3>RVS6>RVS9>RVS12>RVS15，即随着深度的加大紊动强度呈线性递增，这是因为水质点互相混掺的程度决定着紊动强度的大小和水面的波动强度，此时观察DV录像可清晰看到深度9cm高程以上，水体大量混掺运动；ⓑ冲刷裸露至稳定状态下的紊动强度在1～10之间波动，平均值为6.4，是未冲刷Q=13.93L/s状态的8倍，是起冲状态Q=20.05L/s的3.4倍；ⓒ从冲刷特性的云图中可清晰看到在管线周围存在着一个紊动强度波动的核心区域，紊动强度发生值最大，冲刷开后在管线前侧对紊动强度的影响范围大概是管线直径的2.5倍，管线后侧对紊动强度的影响范围是管线直径的2.2倍。

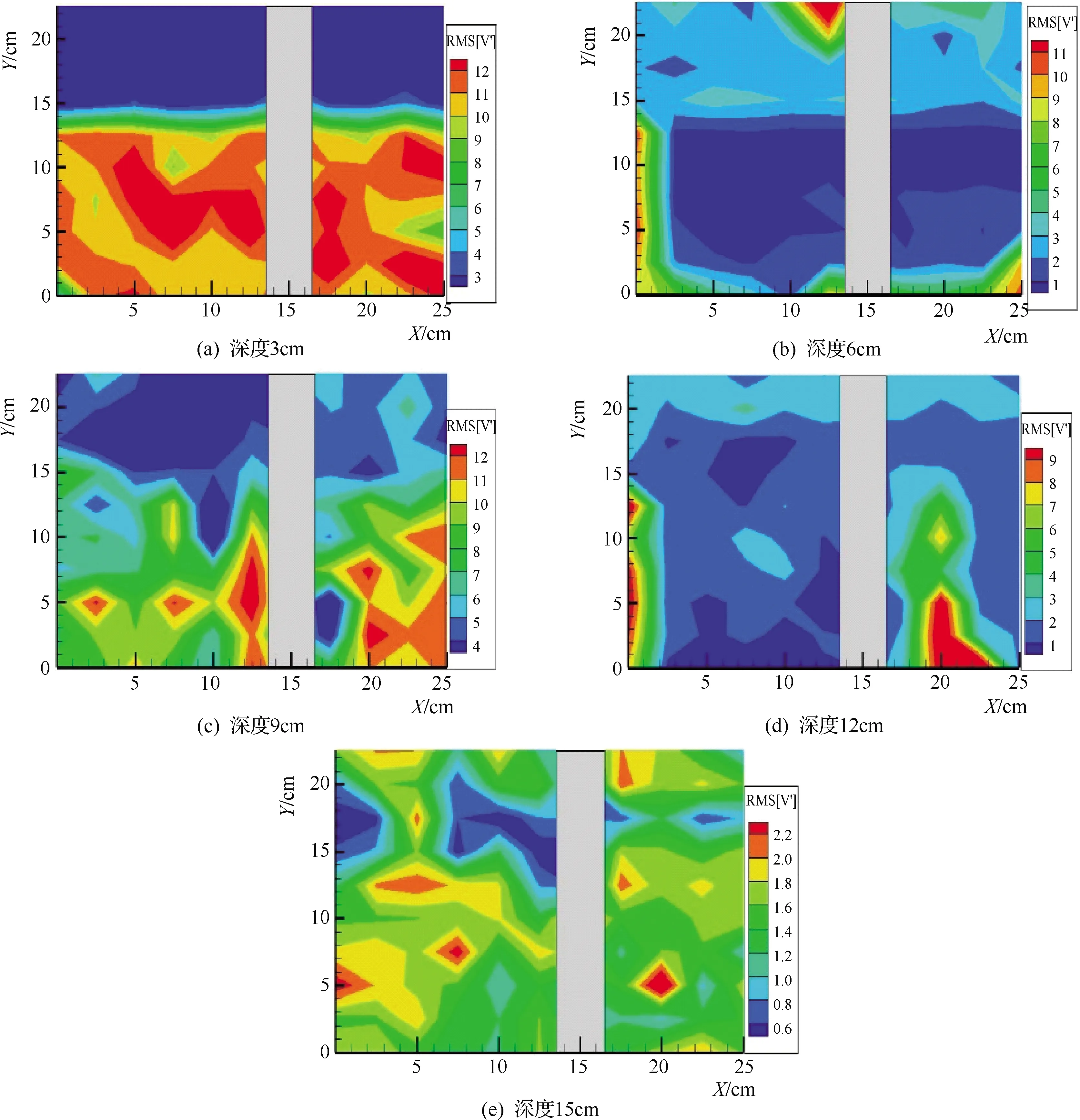
图8 不同层基于Q=25.03L/s的紊动强度云图

3 雷诺应力状态分析

3.1 未冲刷时管线周围雷诺应力特性

基于未冲状态和Q=13.93L/s的截面雷诺应力演变曲线见图9。

图9曲线揭示，未受水流冲刷时，管线处在13.5cm深度处，雷诺应力多于-1.0～1.0之间波动，临近管线周围会发生雷诺应力核心区域，在管线后侧方雷诺应力发生值最大，该区域中雷诺应力尽管发生负值，但负值仅表示了方向，绝对值大小会比其近边其他区域数值高出很多，因为深度小故紊动强度相对较大，导致雷诺应力有所增加。

3.2 起冲时管线周围雷诺应力特性

基于起冲状态和Q=20.05L/s的截面雷诺应力演变曲线见图10。

图10曲线揭示，此情况下的雷诺应力在-2.5～2.0之间波动，是未冲刷情况下雷诺应力平均值的2.25倍。管线设埋于13.5cm横坐标部位，图线清晰可见，管线后方出现雷诺应力的升高区域，升高影响区域大致为1.5倍管径，可知在大水流的状态时此区域管线会遭受较大掏刷冲蚀，因此越河管线抗冲刷保护，该区域应被列为重点强化对象。

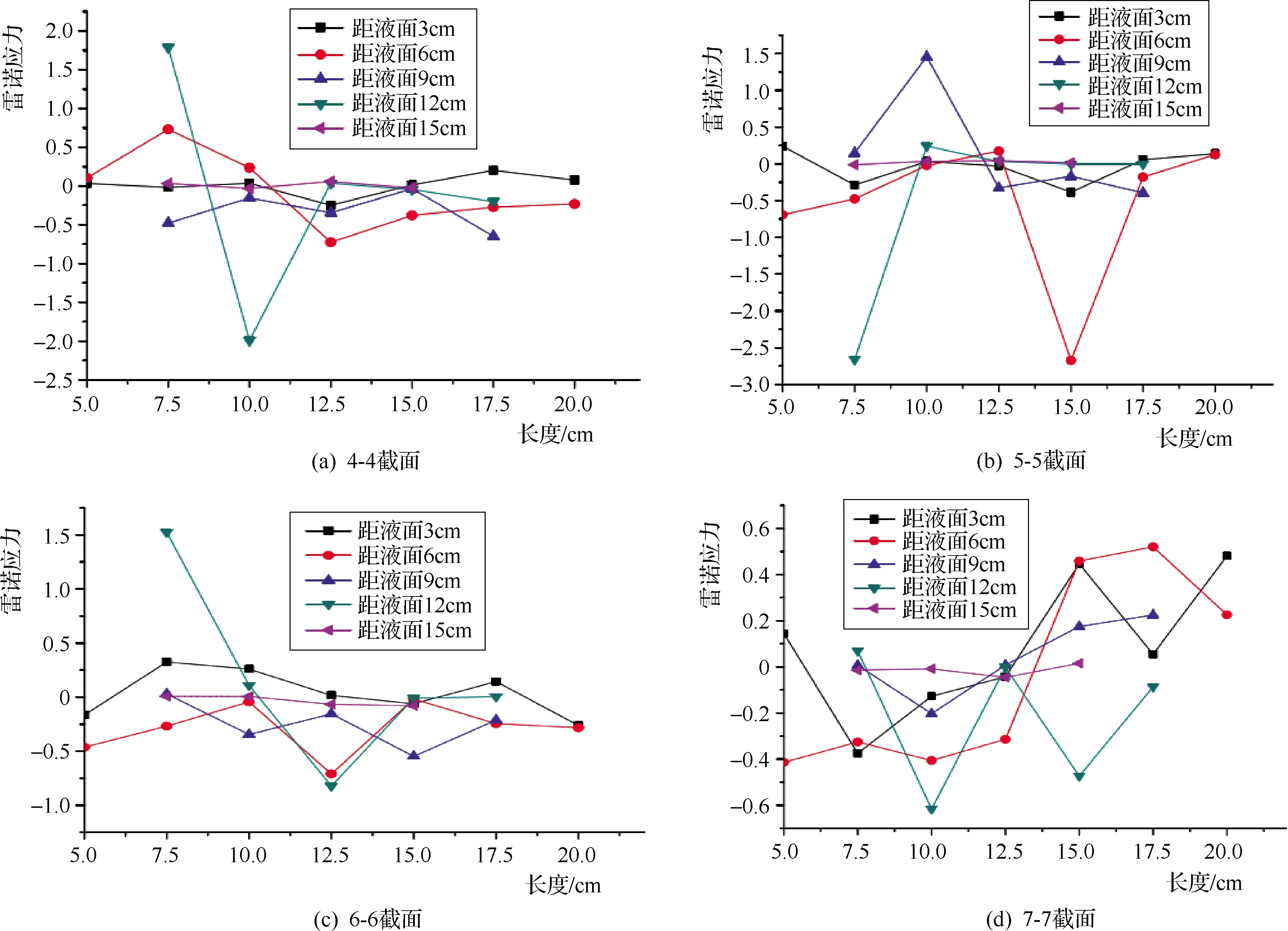
图9 基于未冲状态和Q=13.93L/s的截面雷诺应力演变曲线

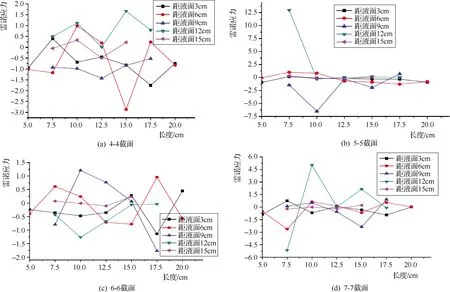
图10 基于起冲状态和Q=20.05L/s的截面雷诺应力演变曲线

3.3 冲刷裸露至稳定状态时管线周围雷诺应力特性

基于冲刷裸露和Q=25.03L/s的截面雷诺应力演变曲线见图11。

图11曲线揭示，此情况下的雷诺应力在-5.0～5.5之间波动，是未冲刷情况下雷诺应力平均值的30倍，是起冲状态雷诺应力的2.33倍。此时深度不同的雷诺应力数值大小杂错分布，不同于流动速率不同深度的规律性，可能缘于露出管线对水流的阻碍作用，同时在大过流量情况下，相对未冲刷与起冲状态，水体所携带的能量大得多，质点间混掺能力强，才导致点线图的杂乱。管线后侧17.5cm处，雷诺应力变动趋向相对稳定，影响范围为4cm，是管径的1.8倍，此范围内应对管线加以保护。

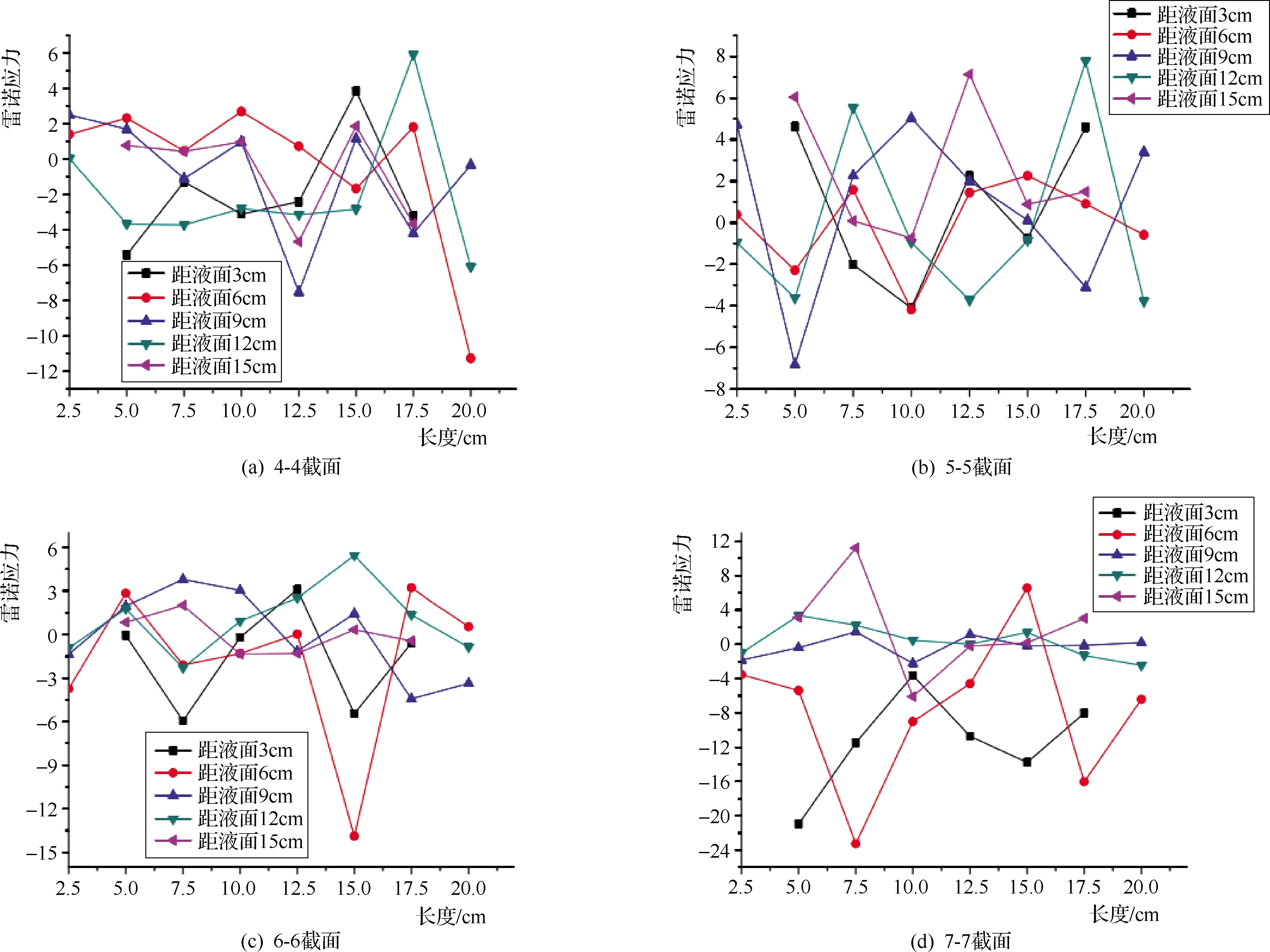
图11 基于冲刷裸露和Q=25.03L/s的截面雷诺应力演变曲线

4 结 语

本文借助实验室比尺模拟实验的方式，对河道管线冲刷的紊动强度及雷诺应力特性进行了专题分析探究。主要获得以下研究成果：

a.开展了泥沙河道管线冲刷紊动强度基本特性分析。实验揭示，冲刷过程中，管线周围存在着一个紊动强度波动的核心区域，会发生最大紊动强度值，管线前侧紊动强度的影响范围大概为管线直径的2.5倍，管线后侧紊动强度的影响范围一般为管线直径的2.2倍。

b.开展了泥沙河道管线冲刷雷诺应力状态分析。实验揭示，冲刷过程中，管线后方出现雷诺应力的升高区域，升高影响区域大致为1.5倍管径。

c.分析揭示，穿河管线不论在未冲刷状态、起冲状态还是冲刷至裸露状态，均为中层液面以上区域的雷诺应力与紊动强度数值较大，两者影响大致分布于1.5倍管线直径的管线后方范围内，此范围内应对管线加以保护。起始冲刷后，水体中层的流动速率影响较大，埋设管线应该尽可能靠近沙泥底层。本实验所探究的泥沙河道管线未冲刷、起冲刷、冲刷裸露至稳定工况下的管线紊动强度和雷诺应力变动规律，可为同类泥沙河道管线工程设计建设提供实验数据参考，以助力建设和维护安全牢固的穿越河道管线工程。