Proximal Point-Like Method for Updating Simultaneously Mass and Stiffness Matrices of Finite Element Model

，

College of Science，Nanjing University of Aeronautics and Astronautics，Nanjing 211106，P.R.China

Abstract:The problem of correcting simultaneously mass and stiffness matrices of finite element model of undamped structural systems using vibration tests is considered in this paper.The desired matrix properties，including satisfaction of the characteristic equation，symmetry，positive semidefiniteness and sparsity，are imposed as side constraints to form the optimal matrix pencil approximation problem.Using partial Lagrangian multipliers，we transform the nonlinearly constrained optimization problem into an equivalent matrix linear variational inequality，develop a proximal point-like method for solving the matrix linear variational inequality，and analyze its global convergence.Numerical results are included to illustrate the performance and application of the proposed method.

Key words：model updating；proximal point method；optimal matrix pencil approximation；matrix linear variational inequality

0 Introduction

It is necessary to build highly accurate mathematical models for analyzing，predicting and controlling the dynamic response of actual structures，such as automobiles，aircrafts，satellites and so on.The analytical model of an undamped system withndegrees of freedom，obtained by finite element methods，can be represented by

wherex（t），f（t）∈Rnare the displacement and external force vectors，respectively，andMa，Ka∈Rn×nare the analytical mass and stiffness matrices.In general，MaandKaare symmetric，sparse and positive semidefinite matrices（denoted byMa≥0，Ka≥0）with special zero/nonzero patterns.The natural frequencyωand the corresponding mode shapexof the system can be obtained via the following characteristic equation or generalized eigenvalue problem

Using eigensolvers［1］，we can compute the frequenciesand the corresponding mode shapesof the finite element model（1）.On the other hand，some of the lower order frequencies（i=1，…，m≪n）and corresponding mode shapesof the real structure can be obtained experimentally by performing vibration tests on the structure.Owing to the complexity of the actual structure，the finite element model is an approximate discrete analytical model of the continuous structure.The analytically evaluated dynamic behavior of the structure seldom agrees with the corresponding experimentally measured ones.The engineer would like to correct the mass and stiffness matrices of the existing structure such that the updated finite element model predicts accurately the observed dynamic behavior.Then the improved finite element model may be considered to be a better representation of the structure than the original finite element model，and can be used with more confidence to analyze，predict and control the dynamic responses of the structure.

Over the past years，many methods［2-3］have been developed for correcting finite element model to predict test results more accurately.The most common approach is to correct the analytical mass or stiffness matrix with minimal deviation from the finite element model by imposing the characteristic equation and the desired matrix properties as side constraints.

Assume that the analytical mass matrixMais exact.Imposing the characteristic equation and the symmetry of the stiffness matrix as side constraints，Baruch［4］and Wei［5］obtained closed-form solutions of the updated stiffness matrix by using Lagrangian multipliers.However，these methods do not guarantee the positive semidefiniteness of the updated stiffness matrix.Based on the QR-factorization of measured mode shapes，Dai［6］proposed an expression of the updated stiffness matrix.Using a decomposition of the stiffness matrix，Kenigsbuch et al.［7］presented the closed-form solution of the updated stiffness matrix.The stiffness matrices corrected by these two methods not only satisfy the characteristic equation and are symmetric positive semidefinite.In all the aforementioned methods，however，the analytical stiffness matrix is adjusted globally，and the sparsity or the zero/nonzero pattern of the stiffness matrix is not taken into consideration.Kabe［8］，Sako and Kabe［9］developed a method and its direct leastsquares formulation for updating stiffness matrix by imposing the characteristic equation，the symmetry and connectivity of the stiffness matrix as side constraints.Applying the theory of inverse problems for symmetric matrices［10-11］，Li et al.［12］presented a method for updating stiffness elements in local error model.But these methods fail to guarantee that the updated stiffness matrix is positive semidefinite.Recently，Yuan［13-15］considered the problem of finding the least change adjustment to the analytical stiffness matrix subject to constraints including characteristic equation，symmetry，positive semidefiniteness and sparsity of the stiffness matrix，transformed the problem into the dual problem and the matrix linear variational inequality，and presented a subgradient method，a projection and contraction method，and a proximal-point method，respectively.

Using experimentally measured mode shapes，Berman et al.［16］sought the least change adjustment to the analytical mass matrix subject to both the symmetry of the mass matrix and the orthogonality relation，and derived an expression of the updated mass matrix by using Lagrangian multipliers.Zhang［17］，and Lee et al.［18］obtained the explicit expressions of the updated mass matrix by using matrix transformation method and the Moore-Penrose inverse，respectively.However，the mass matrices corrected by these expressions not only change the sparsity of the analytical mass matrix，but also are not necessarily positive semidefinite.In order to maintain the sparse structure of the analytical mass matrix，Wei and Zhang［19］，and Cha［20］proposed the analytical mass matrix modification method via element correction，but the updated mass matrix fails to be positive semidefinite.Recently，Dai and Wei［21］considered the problem of correcting the analytical mass matrix subject to constraints including symmetry，orthogonality relation，positive semidefiniteness and sparsity of the mass matrix，and presented a cyclic projection method.

Combining the analytical mass matrix modification with the analytical stiffness matrix adjustment，Baruch［22］，Berman and Nagy［23］，Kenigsbuch and Halevi［7］，Cha and Gu［24］，Wang and Yang［25］proposed procedures to adjust alternately analytical mass and stiffness matrices.The mass and stiffness matrices are related by the characteristic equation，therefore it is conceivable that simultaneously correcting the mass and stiffness matrices will yield better results than sequential correction.Dai［26］，Wei［27］，Kenigsbuch and Halevi［7］considered the problem of simultaneously updating the analytical mass and stiffness matrices.However，the analytical mass and stiffness matrices are adjusted globally in these methods.Recently，Yuan and Dai［28］investigated the problem of simultaneously correcting the analytical mass and stiffness matrices to satisfy characteristic equation，symmetry，positive semidefiniteness，orthogonality and sparsity，and presented a subgradient algorithm for solving the problem.However，the computational cost of the subgradient algorithm is expensive and the measured mode shapes may not satisfy orthogonality before the mass matrix is determined.More recently，Wang and Dai［29］developed an alternating projection method for simultaneously correcting the analytical mass and stiffness matrices.Using the vectorization and the Kronecker product of matrices，Rakshit and Khare［30］proposed a novel solution approach for the finite element model updating problem with no spillover.The approach preserves symmetric band structure of finite element model，but fails to guarantee that the updated mass and stiffness matrices are positive semidefinite.

For convenience，we use the following notations.For a matrixA，tr（A），ATand‖A‖2denot e the trace，transpose and spectral norm ofA，respectively.ForA，B∈Rn×m，andA2Bdenote the inner product and the Hadamard product ofAandB，respectively，and the matrix norm ‖A‖Fis th e Frobenius norm induced by the inner product.SRn×ndenotes the set of alln×nsymmetric matrices andSR0n×nis the set of all symmetric positive semidefinite matrices in Rn×n.A≥0 means thatAis a real symmetric positive semidefinite matrix.The vector inequalityx≥0 is meant to be componentwise（i.e.，forx=（x1，x2，…，xn）T∈Rn，we writex≥0 ifxi≥0 for alli=1，…，n），and let={x|x∈Rn，x≥0}.ForA，B∈Rn×m，sparse（A）=sparse（B）means that the matrixAhas the same zero/nonzero patterns with the matrixB.LetΛe=di ag（（ω1（e））2，…，（ωm（e））2）∈Rm×mconsist ofmmeasured frequencies，consist ofmmeasured mode shapes and be of full column rank.Without loss of generality，we assume that the analytical mass matrixMaand stiffness matrixKaare symmetric since

holds forM，K∈SRn×n.

In this paper，we consider the problem of updating simultaneously the analytical mass and stiffness matrices with requirements of satisfaction of the characteristic equation，the symmetry，the positive semidefiniteness and the sparsity，and formulate such a problem as the following matrix pencil nearness problem

Using partial Lagrangian multipliers，we convert the nonlinearly constrained optimization problem（3）into an equivalent matrix linear variational inequality.Applying proximal point algorithm（PPA）for variational inequality problems，we develop a proximal point-like method for solving the problem（3）.

The rest of this paper is organized as follows.In Section 1，we transform the sparsity constraints on the mass matrixMand stiffness matrixKinto two equality constraints，and give a brief description of PPA for variational inequality problems.In Section 2，we convert the matrix pencil nearness problem（3）into an equivalent matrix linear variational inequality by using partial Lagrangian multipliers.In Section 3，we develop a proximal point-like algorithm for solving the problem（3），and analyze its convergence.In Section 4，three numerical experiments are performed to illustrate the effectiveness and application of the proposed method.Some conclusions are drawn in Section 5.

1 Preliminaries

1.1 Reformulation of problem（3）

We transform the sparsity requirements on the mass matrixM=(mij)∈Rn×nand the stiffness matrixK=(kij)∈Rn×ninto convenient forms.The zero/nonzero patterns of the matricesmay be definitely described as the following index sets

Based on the sparsity constraints on the mass matrixMand the stiffness matrixKdepending on the zero/nonzero patterns of the matricesMaandKa，We define two auxiliary matricesas follows

The matricesMaandKaare symmetric and so are the matricesTMaandTKa.Yuan and Dai［28］showed that

Then the problem（3）is equivalent to the following convex minimization problem

Obviously，the feasible region of the problem（4）is nonempty.

In order to convert the minimization problem（4）into an equivalent matrix linear variational inequality，we need the following lemmas.

Lemma 1［31］For following convex programming problem

wheref（x）：Rn→R is a continuously differentiable and convex function andΩ⊆Rnis a closed convex set，x*∈Ωis a minimum if

Lemma 2［31］For following constrained minimization problem

wheref（x），gi（x），hj（x）：Rn→R are assumed to be continuously differentiable，its feasible region is denoted byΩ.Letg（x）=（g1（x），…，gm（x））T，h（x）=（h1（x），…，hl（x））T，andL（x，u，v）=f（x）-uTg（x）+vTh（x）be the Lagrangian function of the minimization problem with Lagrangian multipliersandv∈Rl.Assume thatf（x），-g（x）are convex functions，h（x）is a linear function and the minimization problem satisfies the Slater constraint qualification［32］，thenx*∈Ωand，v*∈Rlsatisfy the Karush-Kuhn-Tucker（KKT）conditions［31］if and only if

1.2 Proximal point algorithm（PPA）

LetΩ⊆Rnbe a closed convex set，andF：Rn→Rnbe a mapping.Assume thatF（u）is monotone onΩ，i.e.，for allu，v∈Ω.The variational inequality problem is that of findingu*∈Ωsuch that

A classical method for solving the variational inequality problem is the proximal point algorithm（PPA）proposed first by Martinet［33］，and then developed by Rockafellar［34］，Burachiky and Iusem［35］.For givenuk∈Ω，the new iterateuk+1is obtained by solving the following auxiliary variational inequality subproblem

where ｛βk｝is a sequence of positive numbers called regularization parameters，bounded above.However，it is impractical to solve exactly the subproblem（10）since solving the subproblem（10）may require a computation as difficult as solving the original problem.Many researchers presented some implementable PPAs.Recently，He et al.［36］proposed an implementable PPA method for monotone variational inequalities.The method generates a proximal pointkwhich is the solution of the following proximal subproblem

where the proximal termH（u）is positive definite（not necessarily symmetric）but may not be the gradient of any function，and the new iterateuk+1is updated by

He et al.［36］established the global convergence of the PPA-based method.The parameterγin Eq.（13）is a relaxed factor.In practical computation，takingγ∈［1，2）is wise for fast convergence.

2 Equivalent Matrix Linear Variational Inequality Formulation

Let

thenΩis a closed convex set.LetΔ∈Rm×n，Γ1，Γ2∈Rn×nbe the Lagrangian multiplier matrices corresponding toKXe=MXeΛe，M*TMa=0 andK*TKa=0，respectively.We get the following partial Lagrangian function for the problem（4）

Eq.（14）is defined onΩ.Obviously，the gradient ofL（M，K，Δ，Γ1，Γ2）with respect toM，K，Δ，Γ1andΓ2can be written as

The compact form of Eq.（15）is the following linear variational inequality

We call the problem（16）matrix linear variational inequality（MLVI）.

3 Proximal Point-Like Method for MLVI

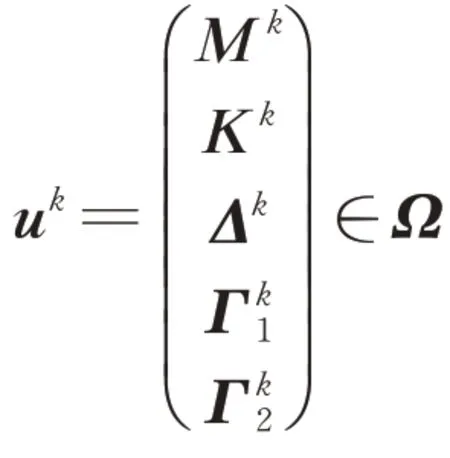
whereH(k-uk)is the proximal term.In this paper，we construct the proximal term as follows

whereu∈Ωands，ri，ti∈R（i=1，2）are positive numbers selected to ensure the positive definiteness of the linear operatorH(u).

It is easy to verify the following lemma.

Remark 1Theorem 2 shows that the linear operatorH（u）is positive definite onΩunder the condition（20）.For convenience，we use the notation，and assume that Eq.（20）holds always.

By Eq.（19），we can decompose the problem（18）into several smaller and easier subproblems as follows

It is easy to find the solutions to the problems（23）—（25）as follows

The problems（21）and（22）are equivalent to the following minimization problems

In order to find the solutions to the subproblems（29）and（30），we need the following Lemma.

Lemma4［37］LetA∈Rn×n，=(AT+A)/2，and the spectral decomposition of the real symmetric matrix=Qdiag(θ1，θ2，…，θn)QT，whereθj(j=1，2，…，n)are the eigenvalues of，Q∈Rn×nis an orthogonal matrix.Then the following problem

has the unique solutionA+which may be expressed by

A+=Qdiag(β1,β2,…,βn)QT

whereβi=max{θi，0}，i=1，2，…，n.

Using Lemma 4，it is easy to compute the solutions to the subproblems（29）and（30），denoted bykandk，respectively.

From Theorem 1，we know that the problem（16）is a monotone variational inequality.Onceare obtained，ukcan be updated touk+1by using Eqs.（12），（13）and（19）.However，this is time consuming.We use the following extrapolation formula to correctuk+1，that is

where the parameterγis a relaxed factor，it is wise to setγ∈［1，2）for guaranteeing the fast convergence［38］.A numerical algorithm for the problem（4）is summarized as follows.

Algorithm 1Proximal point-like algorithm

Input：Ma，Ka，TMa，TKa∈SRn×n，Λe∈Rm×m，Xe∈Rn×m，initial matricesM0，K0∈SRn×n，Δ0∈Rm×n，，toleranceε＞0 andk=0.

Output：Updated mass and stiffness matrices.

（2）Solve the subproblems（29）and（30）to getk，k，respectively；

（3）Compute the new iterateuk+1by using Eq.（31）；

（4）If||uk-k||F＜ε，set the solutionu*=uk+1and exit；else setk：=k+1 and go to（1）.

Now we analyze the convergence of Algorithm 1 and show that Algorithm 1 converges globally.

Lemma 5LetΩ*be the solution set of the problem（16）which is assumed to be nonempty，andu*be a solution of the problem（16）.Ifkis generated from the givenuk∈Ωby Eq.（18）with the proximal termH（u）（Eq.（19）），then

ProofSinceu*∈Ω*，it follows from Eq.（18）and the linearity ofH（u）that

Adding Eqs.（33）and（34）and using Theorem 1，we obtain

Consequently，we have Eq.（32）.

Lemma 6Letkbe the proximal point generated from the givenuk∈Ωby Eq.（18）with the proximal termH（u）（Eq.（19））.Then for allu*∈Ω*，the sequence｛uk｝generated by Algorithm 1 satisfies

ProofIt follows from Theorem 2，Eq.（31）and Lemma 5 that

Lemma 6 shows that the sequence｛uk｝generated by Algorithm 1 is Fejér monotone［39］with respect to the solution setΩ*.

Theorem 3The sequence｛uk｝generated by Algorithm 1 for the problem（16）converges to the solution setΩ*.

ProofFor anyγ∈［1，2），it follows from Theorem 2 and Lemma 6 that｛uk｝is bounded and thus

and thusu∞is a solution point of the problem（16）.Noting that the inequality（36）is true for all solutions of the problem（18），we get

thus the sequence｛uk｝converges tou∞.

4 Numerical Tests

In this section，we present three numerical examples to show the effectiveness and the application of Algorithm 1 for solving the problem（3）arising in structural dynamics model updating.All the numerical tests are carried out in MATLAB.Letandbe the measured lower order eigenvalues and corresponding eigenvectors，respectively，andλiandxi（i=1，2，…，m）be the lower order eigenvalues and corresponding eigenvectors of the updated system，respectively.We useMandKto denote the updated mass and stiffness matrices，respectively.Let

In Algorithm 1，the parametersr1，r2，s，t1，t2inH（u）should theoretically satisfy Eq.（20）.In fact，the parametersonly needs to satisfy the conditions＞0 since some inequalities are overestimated in the proof of Theorem 2，so some of our numerical experiments show that Algorithm 1 converges faster for 0＜s＜1 than fors≥1.

Example 1An undamped spring-mass system，including the spring stiffness and mass values，is shown in Fig.1.

Letmi=1 kg（i=1，2，…，5），ki=0.5 N/m（i=1，2，…，6）.The exact stiffness and mass matrices are given by

We choose three exact lower order eigenvalues and corresponding eigenvectors as the given measured data，denoted byΛeandXe，respectively.

To show the effectiveness of Algorithm 1，the exact stiffness and mass matrices are perturbed by

whereRMandRKare 5×5 symmetric matrices whose entries are generated randomly and distributed uniformly within［-1.0，1.0］，andμis a parameter.In this example，we setμ=0.001.

To implement Algorithm 1，we set the prescribed toleranceε=4.5×10-5，and chooseγ=1.95，s=0.11，andt1=t2=1.001.Algorithm 1 terminates after 159 iterations.Numerical results are reported in Table 1.

Table 1 Numerical results of Example 1

The updated mass and stiffness matrices are obtained as follows

The updated mass and stiffness matricesMandKhave the same zero/nonzero patterns asMaandKa，respectively.It is easy to verify thatM≥0 andK≥0.Table 1 shows that the updated matricesMandKsatisfy the characteristic equation and the differences between the measured eigenpairs and the reproduced ones are very small.

The following two real-life models are built by Patran 2008 r2 and analyzed by Nastran［40］.

Example 2［28］Consider a cantilever with one fixed end and a lumped mass on the other free end.The cross section of the cantilever is like“I”（Fig.2）.The length and height of the cantilever areL1=1 m andL2=0.05 m，respectively.The geometric parameters of the cross section areH=0.1 m，W1=W2=0.068 m，t=0.004 5 m，andt1=t2=0.007 6 m.The elastic modulus is 2.0×1011N/m2，Poisson’s ratio is 0.33，and the density is 7 800 kg/m3.The lumped mass on the free end isF=2 kg.The cantilever is meshed into 40 nodes with 6 degrees of freedom by using finite element method.The 240×240 analytical mass and stiffness matricesandare obtained.has 122 nonzero entries，has 1 098 nonzero entries，and they have special zero/nonzero patterns.

In order to illustrate the effectiveness of Algorithm 1，we choose four lower order eigenpairsof the matrix pencilas the measured eigendata，and set

Table 2 shows that the updated matricesMandKsatisfy the characteristic equation and the differences between the measured eigenpairs and the reproduced ones are very small.It is easy to verify that the updated matrices satisfy symmetry，positive semidefiniteness and sparsity simultaneously.

Example 3［28］The deflection of a plate acted on by a distributed load is considered as shown in Fig.3.The geometric and physical parameters of the plate areh=0.01 m，L=1.2 m，w=0.6 m，elastic modulus 7.0×1010N/m2，Poisson’s ratio 0.33，and density 2 800 kg/m3.The distributed loadF=2 000 N/m3is rigidly supported at its two borderlines.Using finite element method，we mesh the plate into 150 rectangular grids，and obtain 1 008×1 008 analytical mass and stiffness matricesandwith special zero/nonzero patterns.There are 504 nonzero entries inand 14 418 nonzero entries in.

We choose 20 lower order eigenpairsof the matrix pencilas the given eigendata，and setwhereare 60×60 symmetric matrices whose entries are generated randomly and distributed uniformly within［-1.0，1.0］，andμ=0.001 is a perturbed parameter.Lettingε=1×10-3，γ=1.5，s=1.01，，and using Algorithm 1，we obtain the updated mass and stiffness matricesMandKafter 3 636 iterations.Numerical results are given in Table 3.

It is easy to verify that the updated matrices are symmetric and positive semidefinite，and have thesame zero/nonzero patterns asand.Table 3 shows that the updated matricesMandKsatisfy the characteristic equation and the differences between the given eigenpairs and the reproduced ones are very small.

Table 2 Numerical results of Example 2

Table 3 Numerical results of Example 3

5 Conclusions

In this paper，we consider the problem of correcting simultaneously mass and stiffness matrices of finite element model of undamped structural systems using vibration tests，and develop a new analytical model updating method on the basis of the optimal matrix pencil approximation and the proximal point method for solving variational inequalities.In this method，the desired matrix properties，including satisfaction of the dynamic equation，symmetry，positive semidefiniteness and sparsity or connectivity，are imposed，thus preserving the physical and geometric configuration of the analytical model.Numerical examples demonstrate that the new model updating method is effective.