基于DDPG算法的光伏充电站策略优化
2020-05-10江友华帅禄玮曹以龙
江友华, 帅禄玮, 曹以龙
(上海电力大学 电子与信息学院, 上海 200090)
随着电动汽车的发展,充电站的数量也在不断增加。传统充电站只能通过向用户售电获取利润,而光伏充电站由于光伏电源的存在,既可以向用户售电,也可以并网发电获得收益。因此,如何合理分配充电功率和并网功率,以获得最大化利润是充电策略研究的重点[1-4]。
文献[5]采用蒙特卡洛法,分析了光伏充电站在有序充电情况下的充电策略,直观明了,但属于离线优化,需要大量的随机模拟实验,数据利用率过低。文献[6]通过乘子交替方向算法,得到以充电电量和交互电量为优化变量的分布式优化模型,模型比较精确,但由于考虑了分布式的情况,所以模型的复杂度较高。文献[7]通过多目标遗传算法,优化了光伏充电站充电策略,充分考虑了各种条件下的优化情况,但受制于精度问题和局部收敛问题,且只适用于离线优化。文献[8]探讨了不同时间尺度下的分层优化情况,方法简洁,但优化效果受制于时间尺度的划分方法。文献[9]采用了神经网络预测充电数据,预测结果较为准确,但需要大量的样本数据。文献[10]通过负荷优化考虑光伏充电站的储能配置,但分析方法过于繁琐。
为了解决光伏充电站决策优化问题,本文提出了基于深度策略梯度(Deep Deterministic Policy Gradient,DDPG)算法的充电策略。利用DDPG算法优化充电策略,由于DDPG算法中神经网络具有记忆性,使得优化结果也具有记忆性,可以在经验事实的基础上实现在线优化,保证光伏充电站平均利润的最大化。
1 深度增强学习算法
增强学习是机器学习算法的一种,其学习过程更加接近控制系统。在增强学习中,学习的本体被称为智能体,智能体可以在环境中执行动作。类比于控制系统中,控制器对被控对象施加控制量。同时,环境会给予智能体状态输入和回报,类似于被控对象对控制系统的反馈[11]。
智能体通过学习状态、动作和回报,期望在不同的状态中,执行可以得到最大期望回报的动作。若直接将单次回报的最大值作为最大期望回报,就会造成智能体的局部最优,难以兼顾全局。因此,增强学习引入了值函数作为对期望回报的估计,公式为
(1)
式中:Qv(s,a)——目标优化函数;
R(s|s′,a)——在状态s执行动作a后转化到状态s′的回报函数;
γ——衰减因子;
P(s|s′,a)——执行动作a时,由状态s转换到状态s′的概率集合;
S,A——状态集合和动作集合;
maxQv(s′,a)——状态s′下可能得到的函数Qv的最大值。
上述值函数需要有确定的动作a。若a为连续值,则集合P(s|s′,a)的规模为无穷大,故普通值函数只能对离散的动作估值,无法适用于连续动作[12]。
文献[13]提出的DDPG算法是一种深度增强学习算法,使用了基于确定动作策略的演员-评论家算法框架,并在演员部分采用了确定性策略(Deterministic Policy Gradient,DPG)。该算法的核心是4个神经网络,演员部分有2个神经网络(演员网络u和演员网络u′),评论家部分有2个神经网络(评论家网络Q和评论家网络Q′)。其神经网络结构如图1所示。

图1 DDPG算法的神经网络结构示意
2 新能源充电站建模
DDPG算法的关键是建立合理的状态、动作和回报函数。综合考虑决策所需的变量,应获取每个充电桩的需求功率、每台电动汽车的剩余电量、当前时间和光伏输出功率。
假设充电站共有N个充电桩,其中第i个充电桩对应的电动汽车的需求功率为Pni(i=1,2,3,…,N),其剩余电量为Si。
由于光伏电能在一天中是渐变的,不用实时统计,为了降低决策的维度,可以根据光伏典型出力信息表,以15 min为时间间隔,将一天时间分为96段,即t=1,2,3,…,96,因此输入状态可以表示为
St=[Pn1,Pn2,…,PnN,S1,S2,…,SN,t,PV]
(2)
式中:PV——太阳能在t时刻的光伏输出功率。
由于DDPG算法允许以连续量作为输出,所以直接以每台充电桩的输出功率动作表示为
At=[Po1,Po2,Po3,…,PoN]
(3)
式中:Poi——第i个充电桩的输出功率,范围为0~1(最大输出功率归一化)。
采用利润作为回报函数[5],为
(4)
式中:Pt——t时刻充电桩输出的总功率;
Sc——当前的购电电价;
Psun——太阳能的并网输出功率;
nfail——连接时长已到,但未充满所需电量的汽车数量;
Ss——售电电价。
3 优化管理策略的求解流程
DDPG算法的具体流程如图2所示。
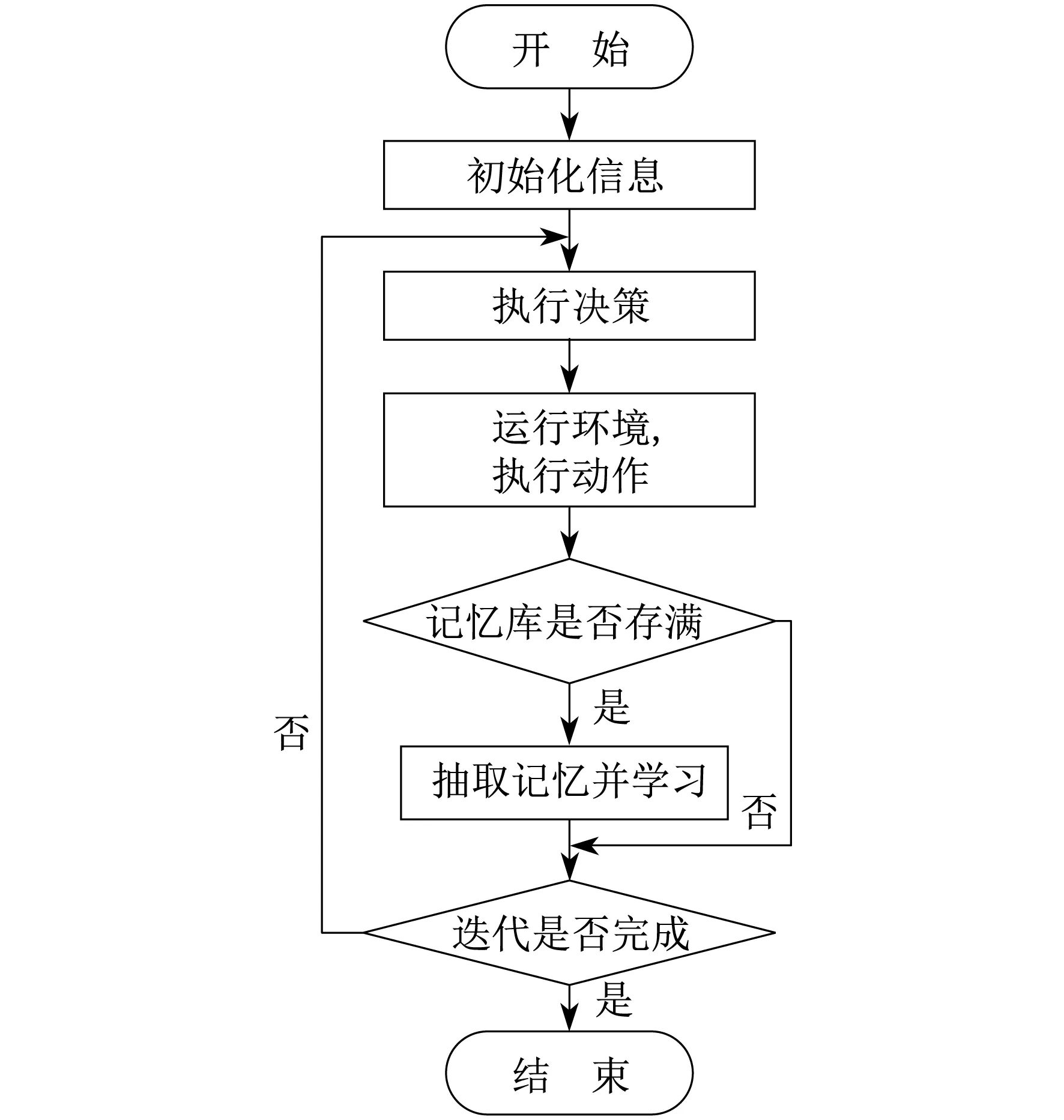
图2 DDPG算法的流程示意
首先,初始化各种数据信息。其次,执行决策部分,获取当前状态St,输入演员网络u,其输出为决策信息,即在当前状态下每台充电桩的输出功率At。再次,运行环境,执行动作,并利用式(4)计算利润Rt,得到下一状态St+1,将St,At,Rt,St+1作为回合记忆存入记忆库。当记忆库存满时,对记忆库进行随机抽样,取得N条回合记忆,并对每条回合记忆进行学习。最后,判断迭代次数是否满足要求,若不满足,则重复上述过程。
4 实 验
实验数据来源于文献[1]。以配置8台充电桩的新能源充电站为例,假设1天中有100辆汽车进行充电。DDPG算法的超参数设置如下:记忆库大小为20 000;神经网络训练的批数量M=32 ;衰减因子γ=0.9;替换步长τ=0.01;评论家网络学习速率为0.001;演员网络学习速率为0.000 5。
评论家网络和演员网络的结构如图3所示。其激活函数采用线性整流函数(Rectified Linear Unit,ReLU)。
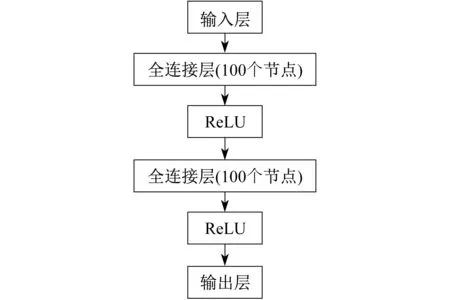
图3 DDPG算法中评论家网络和演员网络的结构
其中,演员网络的输入层节点数为18个,输出层节点数为8个,评论家网络的输入节点数为26个,输出节点数为1个。
8台充电桩一天内的功率输出变化三维图如图4所示。图4中标出的点表示04:00时,1#充电桩上的电动汽车需要6.64 kWh的能量。
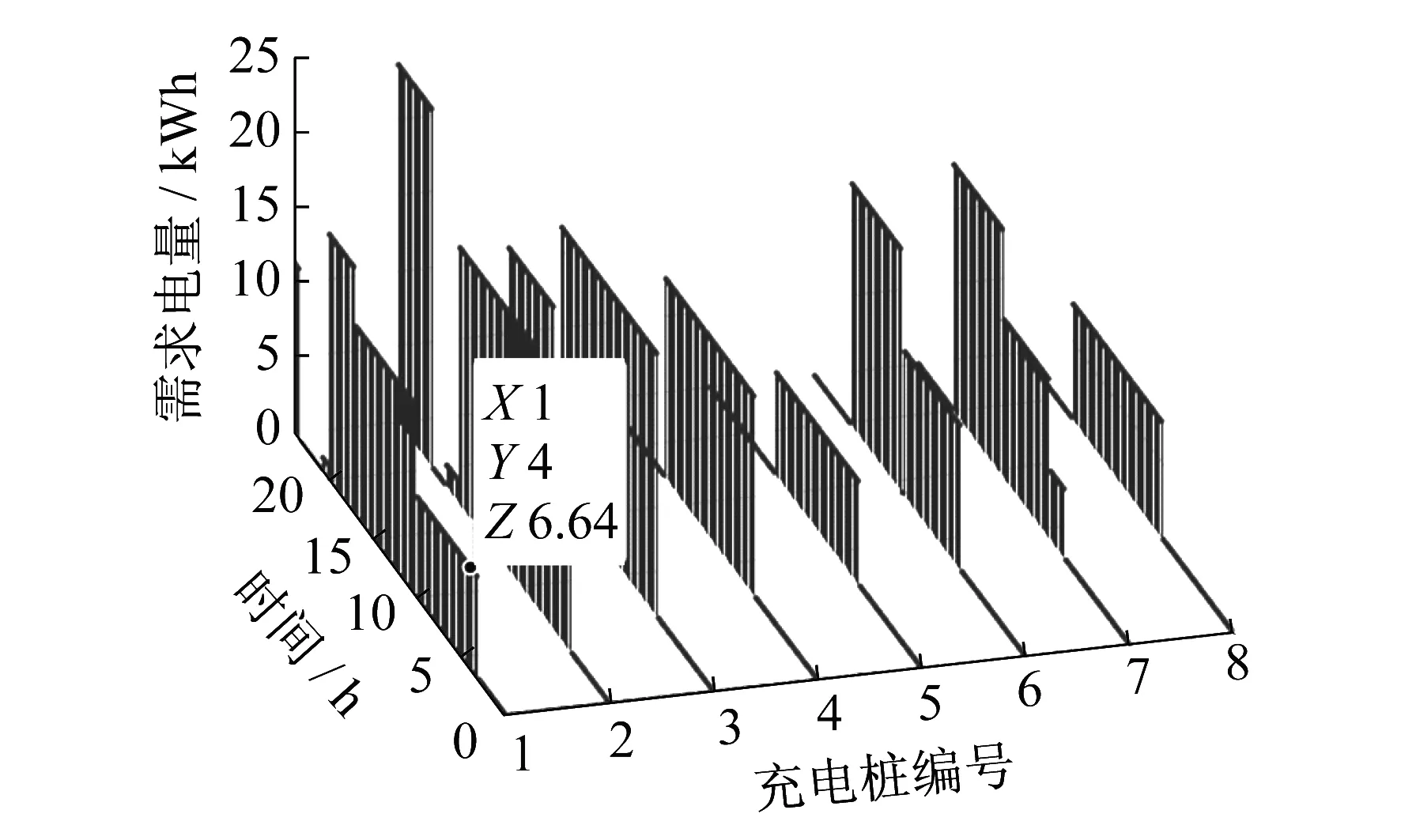
图4 8台充电桩一天内的需求功率变化三维图
DDPG算法中,充电站在光能达到完全利用的情况下的利润曲线如图5所示。由图5可以看出,利润曲线在前期有较大波动,这是算法不断寻优的过程,最终算法会找到一个最优解,其后输出的利润逐渐稳定。
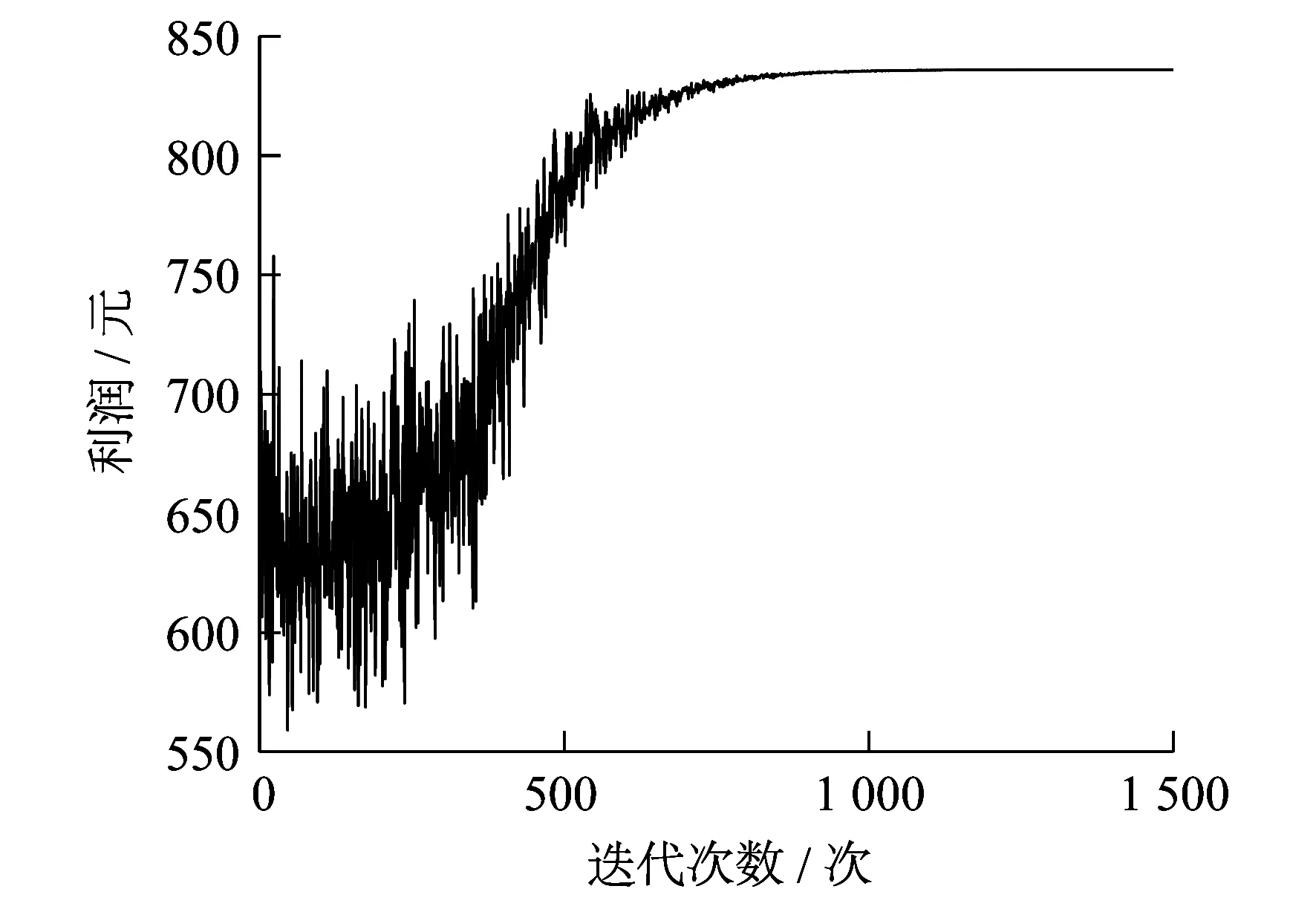
图5 DDPG算法迭代收敛曲线
在不同光照条件下,DDPG算法得到的输出功率如图6所示。此处,采用的光伏电池输出功率表示光照条件。在光照条件较弱时[图6(a)],光伏输出的功率较小,最大功率约为40 kW,且日照时间较短,在06:15时输出功率约为4 kW;在光照条件较强时[图6(b)],光伏电池的输出功率较大,最大功率可到60 kW以上,日照时间较长,在05:00时输出功率接近30 kW。
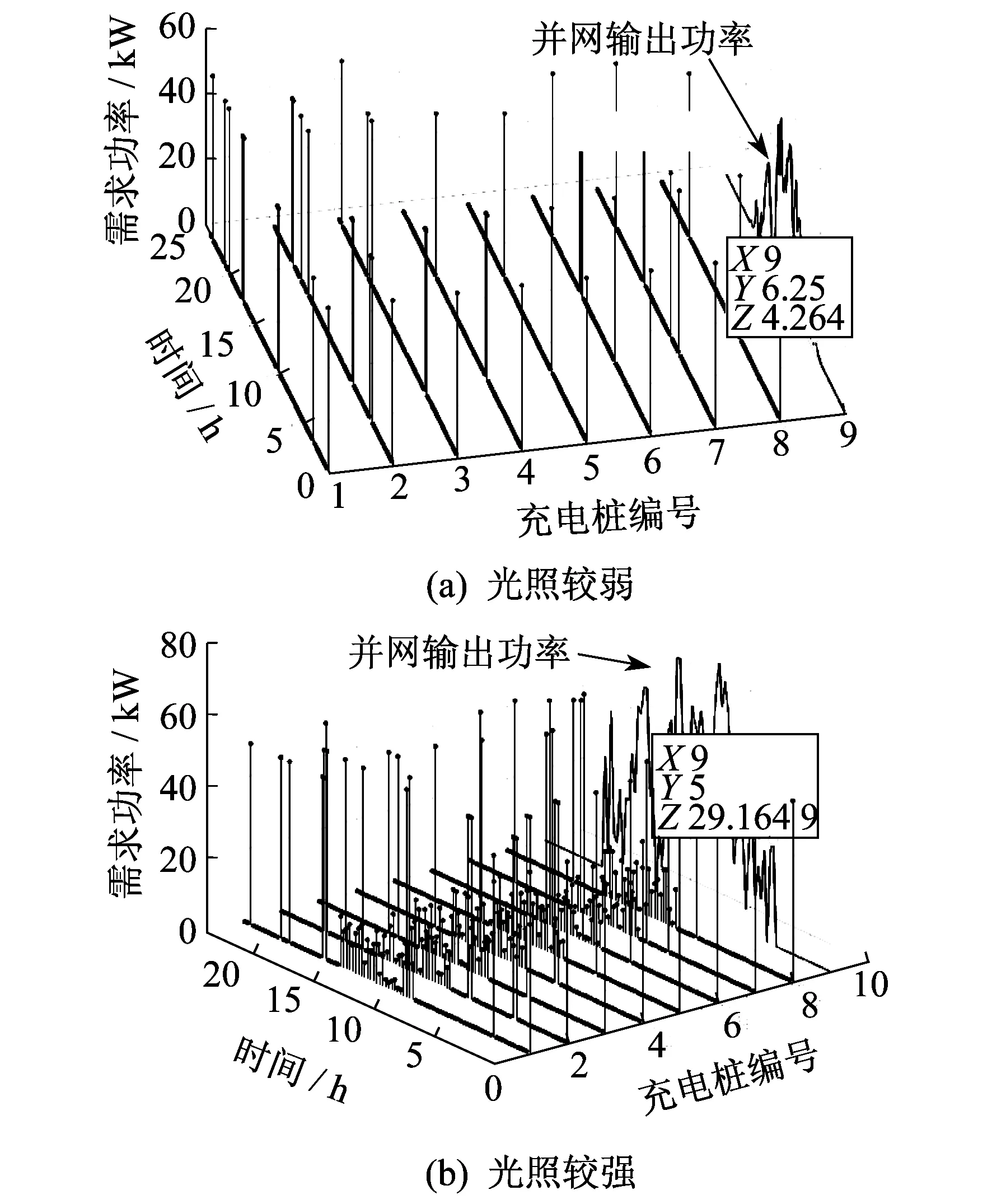
图6 不同光照条件下DDPG算法的输出功率曲线
由图6可知,在光照条件比较充足时,智能体会偏向在光照条件丰富的时候对电动汽车充电,但也没有盲目提升充电功率;在光照条件较弱时,则会采用比较均匀的充电方式。这说明DDPG算法对于不同的光照条件具有良好的适应性。
对遗传算法、布谷鸟算法与DDPG算法在不同车辆数量和不同光照条件下的利润进行对比。其中,DDPG算法的超参数如前文所述,遗传算法和布谷鸟算法参数如表1所示。3种算法的利润曲线如图7所示。

表1 对比实验参数

图7 3种算法的利润对比曲线
由图7可知:在相同情况下,遗传算法的利润由于受到精度与局部收敛的影响,其利润较其他两种算法要低,而在车辆较少时,布谷鸟算法的利润比DDPG算法要高;在光照条件较弱时,布谷鸟算法的利润较高。但在充电车辆数量较多或光照较强时,DDPG算法的利润要高于其他两种算法,优化效果更好。
5 结 论
本文使用DDPG算法对光伏新能源充电站的充电策略进行了优化,通过仿真实验可以证明该优化存在以下优点。
(1) DDPG算法可直接输出动作,解决了Q值学习类算法无法输出连续动作的缺点。
(2) 直接采用利润作为回报函数,使智能体可以追寻利润最大化。
(3) 相较于传统寻优算法,DDPG算法具有神经网络的记忆性,适用于无先验的在线学习,在充电车辆数量较多或光照较强的条件下均能取得相对较高的利润,优化效果较好。
