中国西南地区小时雨量概率分布特征

潘建华

(四川省气象台，四川 成都 610072)

引 言

降水是多尺度、多因素等综合作用的结果，其中短时强降水更具有复杂多变的特性，通过对降水的日变化研究可以了解和掌握当地降水规律，以便更好地开展降水预报及服务工作[1]。随着理论探讨的不断深入以及气象服务需求的提升，极易引发多种灾害和极端事件的短时强降水备受广泛关注[2-4]，尤其是自动气象站的大面积布网及推广应用，小时雨量资料日渐丰富，使得小时雨量的研究和认识得到不断拓展和更新[5-7]，表明在天气预报服务及气象灾害防御中，小时雨量是不可忽视的重要气象要素[8-9]，同时深化了对降水尤其是暴雨物理过程及成因的认识[10-12]。

短历时降水是降水过程中多时空尺度相互作用的结果，在不同地域、不同气候状况下，其表现特征和影响程度各不相同，致使相关研究的侧重点有所不同[13-16]。周盈颖等[13]从强降水事件着手，研究了重庆东北部短时强降水的时空分布特征及概念模型，发现当地短时强降水事件逐年增多，且夜间发生概率最大，其次是午后。冯汉中等[16]从致灾成因出发，认为短历时强降雨是诱发局地泥石流的关键因素。然而，更多的研究则集中在短历时降水概率分布特征的探讨上[17-19]，特别是近年来在大力推进的暴雨、山洪、地质灾害等防御工作中，越发展现出小时雨量概率分布的重要性。国家防汛抗旱总指挥部办公室起草的《山洪灾害预警指标检验复核技术要求》中明确指出，山洪灾害预警指标需要有从5 a一遇到100 a一遇不等的临界雨量[20]，而小时雨量概率分布在阈值确定中有重要作用[21-22]。

西南地区地跨我国第一、二阶梯，地势起伏大，气候类型多样，短历时降水预报难度一直位居全国前列，其引发的灾害及其危害性十分突出，迫切需要对其时空分布特点开展深入研究。参考以往研究思路[23-25]，本文利用中国西南地区300多个气象站小时雨量观测资料，提出拟合系数与区间概率的适应性修正方法，开展小时雨量频率分布和伽马概率密度函数拟合分布的对比分析，探讨小时雨量频率分布与海拔高度的关系，以加深该区域小时雨量概率分布的认识，力图为短时强降水预报及其引发的灾害防御提供参考。

1 资料与方法

1.1 站点与资料

我国西南五省市现有国家级气象观测站点400多个，均于2005年前建成自动气象观测站，十多年的自动观测资料全部进入中国气象局的CMISS(China integrated meteorological information sharing system)业务系统，可提供2005年3月31日20:00(北京时，下同)至2017年10月31日20:00区域内所有站逐小时雨量观测资料。该时间点的划定与业务上的日雨量时界(20:00至次日20:00)相吻合，同时考虑了低海拔地区冬季降水量小，高原地区很多站点冬季无雨量观测的情况。由于自动气象站观测资料的影响因子较多，在进入CMISS系统库时均经过数据质量控制检验，既关注小时雨量与日雨量的相容性，也注重异常值的核查，确保数据的可靠性。

按照中国气象局地面气象观测规范[26]，该类小时雨量包括液态降水和随降随化的固态降水，但不包括冰雹、雪花等固态降水。小时雨量以每小时降水量大于等于0.1 mm作为一次有效记录，而针对某一时段内只有累计雨量的情况，由于无法将累计雨量准确分配到每一个时次上，故而视为缺测。经分析，确定缺测率在5%以下的369个站点的样本为基础数据集，其中大多数站点(93.77%)的缺测率在1%以下(表1)。这369站的海拔高度在138～3342 m之间，主要集中在重庆、四川、贵州、云南4省市。由于西藏仅东边察隅站有资料，四川西北部大片区域无站点资料，故将无资料的区域去除，站点及地形分布见图1。可以看出，中国西南地区(西藏除外)海拔高度大致自东南向西北逐渐升高，四川盆地以及滇、川交界的盐边及周围海拔较低。

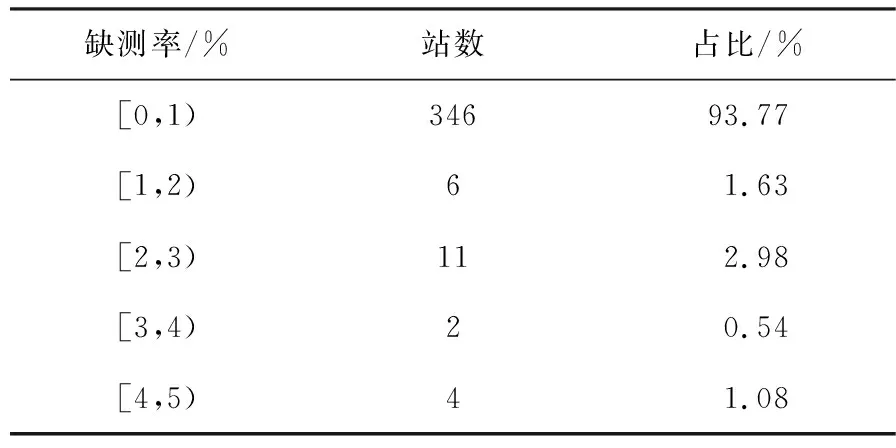
表1 小时雨量数据缺测的站数及比例Tab.1 The numbers and rates of station missing hourly precipitation data

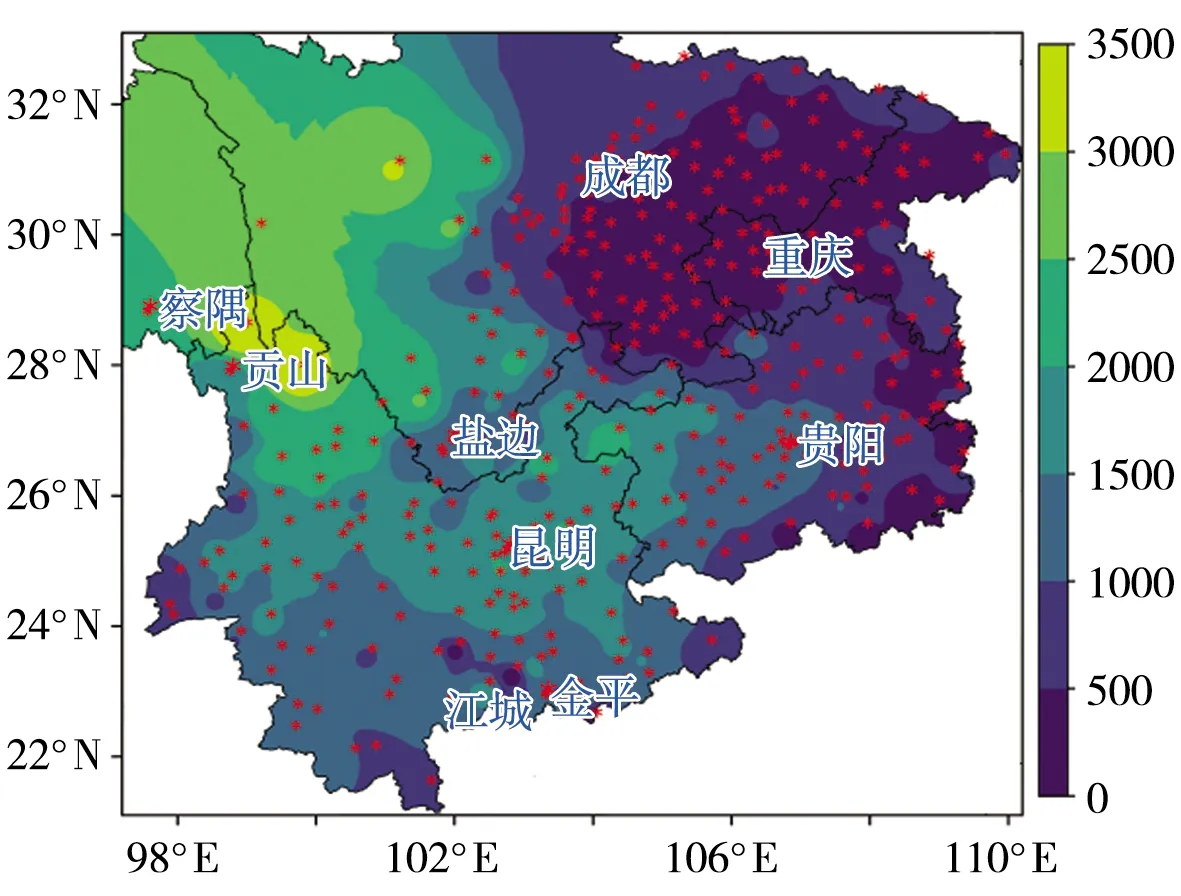
图1 中国西南地区海拔高程(阴影，单位：m)及369个小时雨量站(星号)分布Fig.1 Distribution of elevation (shadows, Unit: m) and 369 meteorological stations (asterisks) in southwestern China

1.2 伽马拟合概率

通常，小时雨量的频率分布表现为低值区频率极高、高值区频率极低的特征，这种频率分布可采用伽马概率密度函数进行拟合[27-28]，其表达式如下：

x>0,α>0,β>0

(1)

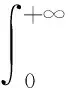
(2)

式中：α和β分别是形状参数和尺度参数。当β一定时，随着α的减小，概率密度大值区逐渐向左靠，α越接近0，概率密度越大，右偏现象越显著，较小量级降水出现的概率越大。β控制着分布函数曲线的拉伸和收缩程度，当α一定时，β越大，各量级降水概率密度分布越集中，反之，则越分散。

概率密度函数中的α和β参数可用最大似然估计[29]来计算得到，表达式为：

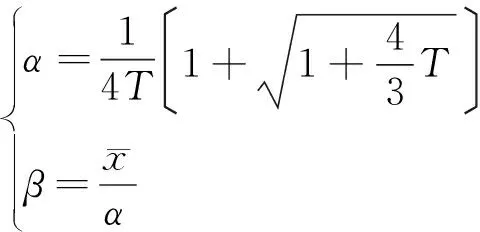
(3)

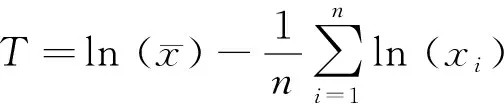
(4)

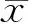
对于某一降水量区间[a,b]，出现降水的区间累积概率可表示为：

(5)

降水量超过某一阈值b的累积概率可表示为：

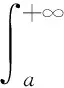
(7)

为便于比较，针对每个站点的小时雨量进行排列，按从小到大均分为31等份，每份即为一个档位，对落入各档位的小时雨量进行计数，从而获得在各档位上的频率。伽马拟合概率是根据(3)式计算得到参数α和β，然后基于(5)和(6)式，利用差分方法获得各档位区间上的概率。

另外，采用反距离加权法对站点小时雨量进行空间插值，该方法能更好地保留要素的极值[30]；采用了统计学中常用的χ2检验、z检验和t检验等方法[31-33]。

2 中国西南地区小时雨量频率分布

2.1 伽马函数拟合概率分布

经计算，中国西南地区单站小时雨量概率密度分布函数的拟合参数α和β分别为0.5～0.9、5～45。在此基础上，构建了各站点的小时雨量概率密度分布函数，并逐站计算各档位概率及χ2检验(样本数31，当显著性水平为0.01时，χ2临界值约52)。检验结果发现，369个站点有354站通过χ2检验，未通过率仅4.07%。由此可见，西南地区绝大多数站点的小时雨量频率分布可用伽马函数进行很好的拟合。

另外，将区域内所有站点的小时雨量归并组成一个全样本序列，对其进行伽马概率密度函数拟合，得到全样本序列的α和β参数分别为0.6115、24.54，与369站各自拟合参数的均值0.6219和24.66非常接近。

图2是基于全样本的中国西南地区小时雨量频率分布及伽马函数拟合的概率分布曲线及局部，发现在第5档位的概率已接近0，但频率还保持较高数值，两者差距极大且基数接近0的状态会造成比值异常大，从而导致对χ2数的贡献急剧增大。在单站拟合中，未通过χ2检验的15站概率和频率曲线的相对布局(图略)与图2类似。

小时雨量的概率与频率在中(11～20)、高(21～31)档位上差异异常大的现象，可通过调整α和β参数值的方法加以修正。根据伽马概率密度分布函数，α和β取值不同，则拟合曲线的形状与尺度不同，从而导致拟合概率发生变化，因此可通过调整拟合参数使得χ2数大幅减小到可接受范围内。通过反复调试两参数值发现，当α、β分别小于一定数值后，χ2数极速增加；当α、β分别大到一定程度时，χ2数会迅速减小到可通过显著性检验的范围，随后，当α、β继续增大时，χ2数缓慢增大。相对小时雨量频率分布，伽马函数中α、β参数可在一定范围内取值使拟合概率通过显著性检验。

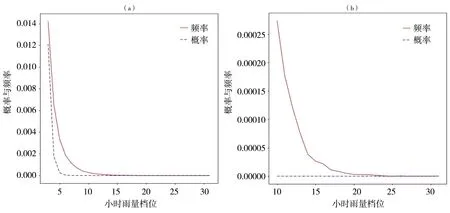
图2 中国西南地区基于全样本的小时雨量频率分布和伽马函数拟合概率分布曲线及其局部(a)第3～31档位，(b)第10～31档位Fig.2 The curves and their local of frequency distribution and probability distribution of hourly precipitation fitted by Gamma function based on total samples in southwestern China(a) from the 3rd to the 31st tap position, (b) from the 10th to the 31st tap position

针对全样本，当0.10 ≤α≤0.70、30≤β≤90 时，分别以0.5和5的步长递进计算，获得多个χ2数。比较发现，当α=0.4、β=60时，χ2数最小，且当α和β分别在该数值的两端一定范围内变化时，χ2数有所增大，且都能通过统计检验。

关于在第1、2档位等出现的频率与概率之间差异较大的现象，可以利用相邻档位衰减率大的特点，通过调整概率计算的差分方法加以修正。依照差分原理，在计算各档位概率时，一种方法是利用档位中点的小时雨量计算概率密度，再乘以档位宽度获得；另一种方法是利用档位两端点的小时雨量计算概率密度后取均值，再乘以档位宽度获得。由于在第1档位、第2档位(部分站点可能是更高的档位)处，概率曲线急剧衰减，表明在这些档位的两个端点以及中点处的概率密度差异很大，故而采用第二种和第一种方法分别计算的档位概率也存在显著差异。基于此特点，可用来对第1档位、第2档位的概率进行修正以减小拟合概率与样本频率之间的差异。需要注意的是，这种修正无法因档位而异，可能会造成在这个档位上减小了频率与概率的差异，而在另一档位上增大了差异，故修正时需考虑在多个档位上的综合效果。另外，在采用第二种方法计算档位概率时，要注意第1档位的下端点取值合理。第1档位的下端点原本取0.1 mm，但由于伽马函数的特性，即在靠近0奇点的该端点处，0.1 mm将导致概率密度奇异地偏大到不合理程度，所以不能取0.1 mm。该端点取值的两个限制条件：一是第1档位的概率不能大于1；二是所有档位的概率之和等于1。综合以上分析，中国西南地区第1档位的下端点取为0.4 mm。

采用上述修正方法，基于α=0.4、β=60以及最低档位起点端为0.4 mm，获得修正后的全样本概率拟合分布。从图3概率分布曲线看出，较低档位上小时雨量的拟合概率与频率之间的差异很小，修正前频率与概率的巨大差异得到显著削弱，两者吻合情况很好，且通过χ2显著性检验。

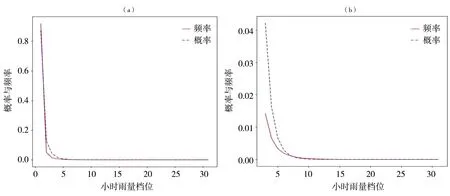
图3 中国西南地区修正后的全样本小时雨量频率和拟合概率分布曲线(a)及其局部(b)Fig.3 The curves (a) and their local (b) of corrected frequency distribution and fitted probability distribution of hourly precipitation based on total samples in southwestern China

需要注意的是，在χ2数可接受的情况下，可以直接选择使χ2数最小的α与β，或是两参数的其他组合。然而，这只是总体比较的χ2数较小，而在各档位，特别是低档位上概率与频率的吻合度并不一定都很高，可附加低档位概率与频率的限制条件，如第1档位的概率和频率相差不能大于10%等，来缩小形状参数和尺度参数的选择范围，从而保证拟合结果能够通过χ2检验。

2.2 小时雨量频率分布特征

2.2.1 小时雨量频率与概率分布对比

为避免不同站点小时雨量极值的显著差异给频率分布曲线对比造成的不便，对小时雨量进行了归一化处理。伽马函数拟合的中国西南地区单站小时雨量概率分布曲线均呈现“L”型分布，这与综合所有站点的全样本拟合结果[图4(a)]相同。各站点小时雨量频率、拟合概率分布形态的差异主要表现为：第1档位频率的大小不同，即曲线起点的高低不同；拐点的高低不同，即档位频率的大小不同。经统计，中国西南地区小时雨量第1档位频率在0.7～0.9之间的有344站，第2档位频率在0.05～0.15之间的有355站，可见绝大多数站点是从第1档位的0.8左右陡降至第2档位的0.1左右，降幅高达约70%；大多数站点在第2、3、4、5档位出现“L”型分布的拐点，且从第6档位开始，频率普遍接近于0，而后极为缓慢地降低到第31档位。其中，在第11档位后，很多站点的频率出现明显的不连续现象，如云南景洪站从第11档位开始，其后很多档位上的小时雨量频率都为0，直至最大雨量所在的第31档位上有一小到无法显示的频率(至少有1个样本)[图4(b)]。这与高强度降水出现概率小、随机性强的特点密切相关，从而造成频率分布曲线的不连续。

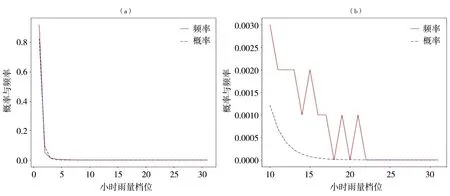
图4 中国西南地区全样本小时雨量频率和拟合概率分布曲线(a)及云南景洪站分布曲线局部(b)Fig.4 The curves of frequency and fitted probability distribution of hourly precipitation based on total samples in southwestern China (a) and the local of distribution curve at Jinghong station of Yunnan Province (b)

综上可见，频率与概率分布曲线尽管视觉上匹配很好，但两者的χ2检验值异常大(1011以上)，无法通过检验，其原因是高档位上频率与概率的差异太大，可通过调整α和β参数值加以修正，使之通过检验。

2.2.2 小时雨量频率与海拔高度的关系

中国西南地区第1档位的小时雨量频率与站点海拔高度有较好的对应关系，海拔高度越高，其小时雨量频率越小。将所有站第1档位的频率均分为6个等级，分别计算各等级的站点数及其平均海拔高度，见表2。可以看出，在第1档位上一级、五级、六级的站点分别不超过2个，尽管这3个等级随站点海拔高度的增加，其频率值呈减小趋势，但由于站点数太少，无法进行统计检验，而对于二级、三级、四级站点样本序列进行的z检验值分别为30.90、 22.31，均通过0.01的显著性检验，表明按照小时雨量在第1档位频率大小划分的二、三、四3个等级之间的站点平均海拔高度有显著差异，在此档位上频率越大，其站点海拔高度越低，两者呈反相关关系，即频率由0.9降低到0.6，站点平均海拔高度由796.3 m升到1559.3 m。

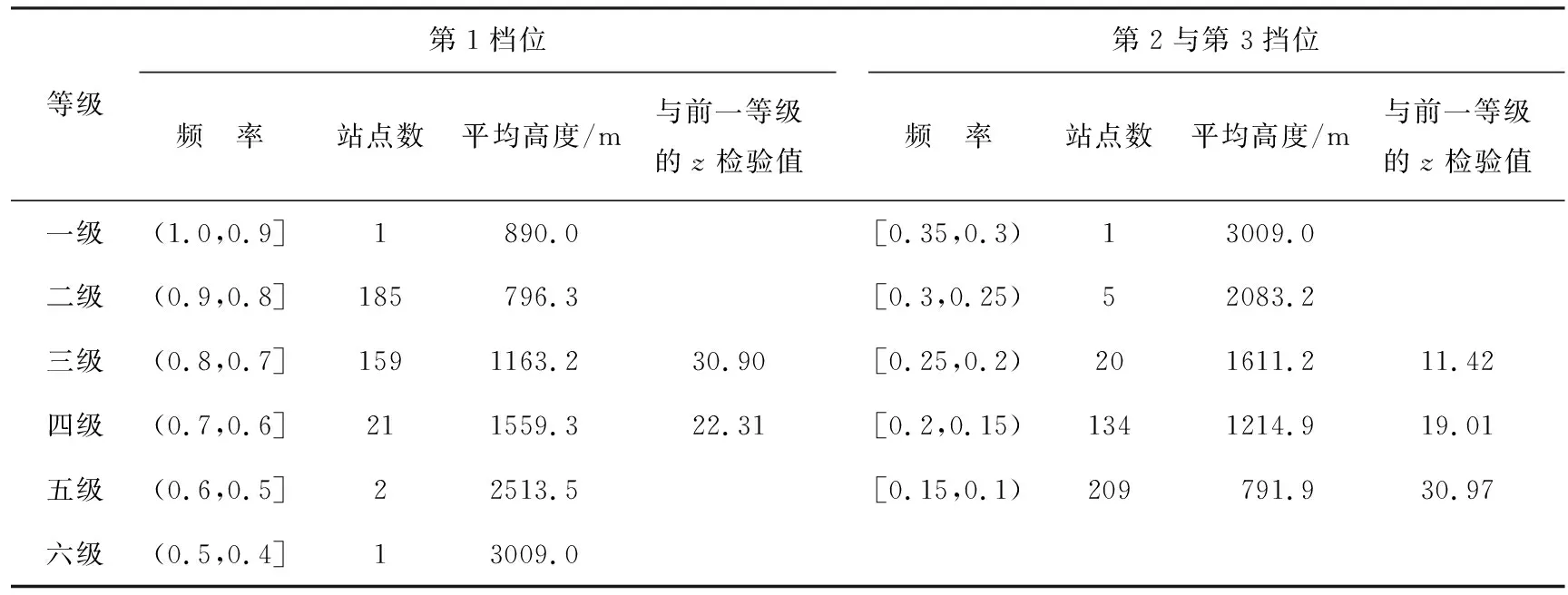
表2 不同档位小时雨量频率分级及对应站点平均高度和相邻等级高度z检验Tab.2 Grades of hourly precipitation frequency in different taps and average height at corresponding stations, andztest of the height between adjacent grades

对第1～2档位和第1～3档位的累积频率进行等级划分，也得到相同的结果，这2组频率的一级与二级站点平均高度的z检验值分别为32.62、22.54(表略)，远大于0.01显著性水平下的临界值，表明相邻等级的站点平均海拔高度有显著差异，其中起主要作用的是第1档位频率。

然而，如果考虑其他档位频率，则会出现完全不同的情况。单站小时雨量频率分布曲线的重要特征之一是“L”型的拐点位置。对西南地区369站小时雨量频率分布曲线观察发现，拐点位置一般在第2、3、4、5档位附近，且随海拔高度增加拐点处频率有增大趋势，即拐点位置升高。从表2看出，各站点第2～3档位的频率和为0.10～0.35，等分的5个等级中一级站点数量太少，没有代表性，可对二、三、四、五级进行z检验，发现相邻等级站点高度的差异均通过0.01的显著性检验，说明随着海拔高度的增加，小时雨量频率“L”型分布的拐点位置升高，即海拔较高的站点在较低档位(第2、3、4、5等档位)上的降水频率比海拔较低的站点在同档位上的高，这和第1档位上频率与海拔高度的关系正相反。针对第2～4档位和第2～5档位上小时雨量频率与海拔高度的关系分析，也得到相同的结果。

2.2.3 拟合参数与海拔高度的关系

对α、β拟合参数进行四等分分级，以落入各等级的站点海拔高度为样本，进行相邻等级的z检验(表3)，可以看出，各等级的站点数分布不均匀，参数α的一级和二级站点数显著偏多，而参数β的二、三级站点数显著偏多；随着参数α(等级)的增大，站点平均高度逐渐降低，而参数β变化正相反，站点平均高度随β(等级)的减小而降低；参数α和β任何相邻等级的站点平均高度均存在显著差异。

结合站点小时雨量频率分布发现，在第1档位上，海拔较高站点的小时雨量频率小于海拔较低站点，而在拐点附近的第2、3、4、5等档位处，前者的频率高于后者，小时雨量频率分布曲线的这种差异体现在α和β的数值上。

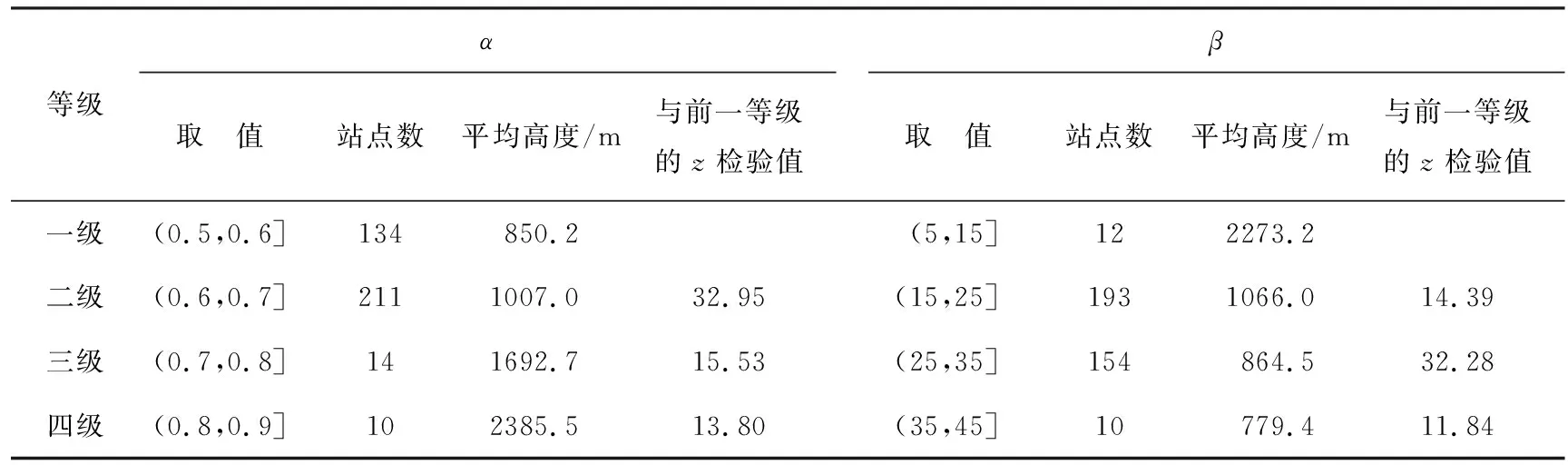
表3 拟合参数分级及对应站点的平均高度与相邻等级高度z检验Tab.3 Grades of fitting parameters and average height at corresponding stations, andztest of the height between adjacent grades

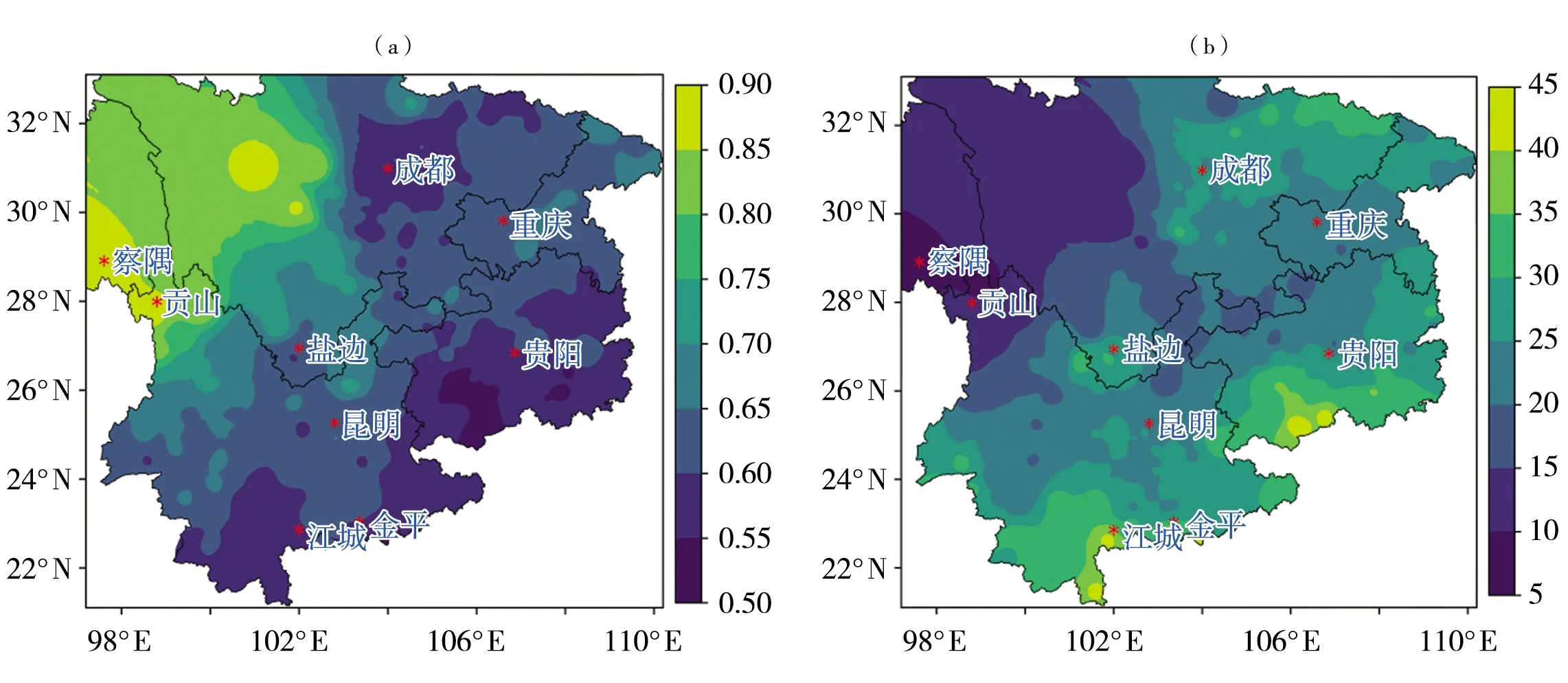
图5 中国西南地区伽马函数拟合参数α(a)和β(b)的空间分布Fig.5 Spatial distribution of fitting parameters of α (a) and β (b) of Gamma function in southwestern China

图5是中国西南地区伽马函数拟合参数α和β的空间分布。可以看出，中国西南地区伽马函数拟合参数α为0.526～0.885，且呈现自东南向西北逐渐递增的空间分布特征，这与海拔高度分布非常吻合[图5(a)]，即参数α随海拔高度增加而增大。其中，四川盆地为α低值中心，而川黔滇三省交界处为高值区。参数β的空间分布也与地形有较高的一致性，四川盆地、川滇交界的盐边站附近更为明显，但β随地形高度的增加逐渐减小[图5(b)]，这与α正相反。

另外还看出，α和β的空间分布与站点高度极为吻合。经计算，α和β与站点高度的相关系数分别为0.4525、-0.3339，仅通过0.05的显著性检验。可见，站点的小时雨量概率分布与站点的海拔高度有关，同时还受周围地形地貌以及盛行风向与天气系统的影响。

3 结论与讨论

尽管中国西南地区地形地貌复杂、高差悬殊、气候差异明显，但区域内站点的小时雨量频率分布一致性特征明显，其结论主要如下：

(1)大多数站点的小时雨量频率分布都可以用伽马概率密度函数进行拟合。

(2)各站点小时雨量频率分布曲线呈“L”型分布，在统一划分的31个档位中第1档位的频率在0.8左右，第2档位的频率在0.1左右，两档位间的衰减率约70%，之后各档位的衰减显著降低，且高档位上还出现频率不连续现象。

(3)在“L”型分布中，第1档位的小时雨量频率随海拔高度的升高而减小，而拐点处档位的小时雨量频率却随海拔高度的升高而增大，即海拔越高地区站点除第1档位外的低强度小时雨量所占的比例更大。

(4)伽马函数中的α和β拟合参数与地形分布非常吻合，且两参数与站点海拔高度分别呈显著正、负相关关系，即海拔越高，形状参数α越大，尺度参数β越小；反之亦然。

多数情况下可以直接利用伽马概率密度函数拟合小时雨量分布，但少数情况下需要采用不同的差分方式、合理选择第1档位的起点值以及根据χ2数主观调整α和β值等方式来提高拟合度，获得能通过统计检验的结果，但这将会影响到概率分布曲线的唯一性。此外，站点周边一定范围内地形的综合效应会对站点的小时雨量频率分布产生较大影响，因此可将小时雨量频率内插到更高的空间分辨率上，以适应特定地区对致灾雨量阈值的需求。