基于小波分析的矿用通风机故障诊断研究

张永杰

（五矿邯邢矿业有限公司 西石门铁矿机动科，河北 武安056300）

0 引 言

矿用通风机是保障煤矿企业正常有序生产的重要动力设备，在煤矿开采过程中起着重要的作用[1]。然而由于煤矿开采的工作环境交叉，通风机的电动机在正常运行时需要承受较大的电压、电流及剧烈的振动，同时受限于电动机轴承的制作工艺，其转子自身存在一定的缺陷，极易发生转子断条及开裂，人工巡检方式很难提前发现隐患故障[2]。因此，研究矿用通风机的故障诊断技术，对于提高矿用通风机的运维水平，具有重大实际生产指导意义，预测的故障诊断结果可在一定程度上分析通风机的故障特征，对于提前安排检修运维，可有效地减少通风机运行中因发生故障而带来的一系列危害[3-4]。

对于矿用通风机故障诊断而言，国内外学者也开展了一系列的研究。常用的方法有时域分析方法和频域分析方法，时域分析方法实现简单，但难以清晰分析复杂工况下的电动机振动故障特征[5]。传统的电动机轴承故障诊断频域分析方法大都采用的是傅里叶变换分析方法，该方法在分析平稳故障信号时具有良好的效果，但是通常电动机轴承设备故障存在突变性，故障信号呈现非平稳特征，导致故障信号含有大量噪声信号，此时采用傅里叶变换难以提取有用信号的故障特征[6]。

针对上述问题，本文提出了一种基于小波分析的煤矿通风机故障诊断方法。该方法首先利用小波分析方法对采集到的通风机轴承振动数据进行降噪处理，然后利用Hilbert变换求解出小波降噪后特征信息的故障特征频率，可有效提高矿用通风机故障诊断的精度。

1 小波分析及降噪

1.1 小波降噪分析

小波分析方法的思想来源于傅里叶分析方法，其具备了傅里叶分析法的局域化分析特征，同时弥补了其在局域化分析中的不足，对工程信号的突变具备良好的观测效果[7]。小波分析方法可以根据实际运行情况自动调节其窗口的大小及形状，同时其时间分辨率也能够根据信号的频率自动调整。具体来讲就是低频信号能够通过窗口变长来获取，而高频信号则通过窗口变短来获取，即实现窗口的自适应调整。

和传统的傅里叶变换相一致，小波变换分析法可将一个信号分解为多种不同频段分量的叠加，而对应的权重和特定的小波具有一定的关联性。通过对基本小波函数进行变换可以求得小波函数，其是小波函数的基本组成部分，能够实现信号的多尺度分析。小波基函数是对基本小波函数进行平移和延伸所求得的，其表达式为

式中：a为尺度因子；b为平移因子；Ψ为基本小波函数。

因此，连续小波变换的定义为

1.2 小波降噪

矿用通风机在实际运行过程中，其轴承振动信号包含各种高频的干扰噪声，因此需要剔除该类干扰信号。为获取小波到实际数据信号的最佳映射，需要将原始的信号从噪声中分离出来，因此需要进行小波降噪。小波降噪可看成是低通滤波的过程，其基本原理是将高频噪声信号滤除，但不同于传统的低通滤波器，小波降噪还能够保留低频信号的原始特征，有效结合了低通滤波及特征保留提取的优点，小波降噪的基本流程如图1所示。

图1 小波降噪过程

小波降噪的基本原理是：原始信号在小波变换下映射到对应的小波域，实际真实信号和噪声信号的小波变换系数存在差异性，因而根据该系数的差异性进行去噪处理。在降噪过程中，本文采用的是阈值降噪函数方法，该方法实现简单、效果较好，其基本实现途径是对小波分解系数设定阈值，来处理原始信号的小波系数，然后反变换得到所需信号。因此，可通过减少噪声信号的小波系数而最大限度地保留实际真实信号的小波系数，随后进行信号重构，从而在实现消除噪声的同时保留实际可用信号的特征。

阈值降噪函数方法采用的是硬阈值及软阈值降噪方法，设置绝对值小的系数为0，对绝对值大的系统进行保留和收缩，其中硬阈值和软阈值分别为：

硬阈值：

软阈值：

式中：x为变量；λ为小波阈值；sign(.)为符号函数。

阈值降噪函数中的阈值选择方法为

式中：l为信号层数；Nl为第l层细节信号长度；δl为第l层细节信号噪声标准差。

δl的计算公式如下：

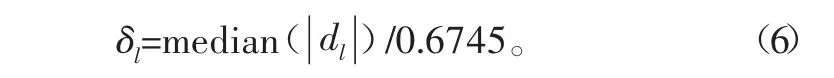
式中：median(.)为中值层数；dl为第l层细节系数。

综上，小波分解的基本步骤可总结为：1）对原始的信号进行小波变换；2）用阈值降噪函数方法处理小波系数，减小噪声的小波系数；3）对小波系数进行逆变换，重构处理之后的小波系数，得到降噪之后的信号。

2 Hilbert 变换

Hilbert变换能够对时域信号的包络谱进行提取，实现调制信号的解调[8]。在矿用通风机轴承故障诊断中，轴承固有的高频信号会调制故障特征频率，采用Hilbert变换能够有效分析振动信号。信号经过Hilbert变换之后会产生一个90°的相移，能够与初始信号形成一个解析的信号，即可构成信号的包络信号。

信号x（t）经过Hilbert变换的定义可表示为

因此，信号x(t)的解析信号可以表示为

式（8）代表原始信号的包络，经过FFT变换后可得

式中：f为信号傅里叶变换；sgn(x)为符号函数；X（f）为x（f）在频域中的相位移。

因此，Hilbert变换能够实现调节功能，轴承故障的振动信号通过Hilbert变换后，可清晰地显现轴承的故障信号。

3 实例分析

以某煤矿的矿用通风机为例进行分析，该通风机的滚动轴承在运行中存在表面损伤的可能，一旦滚动体经过损伤表面会产生交互变化的激振作用力，而滚动表面的损伤呈现不规则的变化会导致多种振动频率的产生。轴承振动机理表明，轴承的滚动形态和旋转速度共同决定了整个轴承的最终振动频率。

记录矿用通风机实际的一组轴承振动信号数据，该组数据的数量为234 839个，采样的频率为50 kHz。采集到的振动信号数据经过运算处理传送至计算机中，采集信号的时域图和频域图分别如图2和图3所示。

对图2和图3中的信号进行降噪处理，采用上述阈值降噪函数方法，选用db5型的小波基函数，降噪分解后的时域和频域图分别如图4和图5所示。从降噪结果可知，采用本文所提的降噪方法能够有效抑制高频噪声干扰。

降噪后的信号经过分解后重构，并采用Hilbert变换进行解调和细化谱的分析，如图6所示。由图可知，降噪后的信号再经过Hilbert变换能够进一步消除高频干扰信号，可清晰地筛选出振动信号的故障特征。

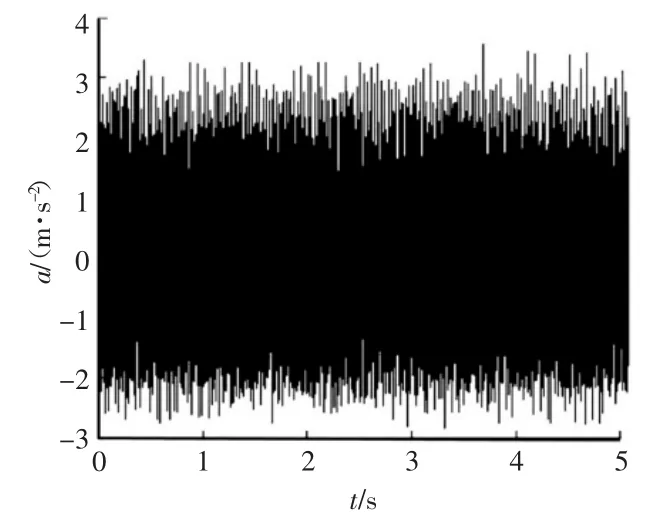
图2 采集信号时域图

图3 采集信号频域图

4 结 论

本文提出了一种小波分析的矿用通风机故障诊断方法，该方法首先利用小波分析方法对采集到的通风机轴承振动数据进行小波分析，并采用阈值降噪函数方法进行信号降噪处理；然后对降噪后的特征信号进行Hilbert变换，求解出特征数据中的故障特征频率。实例测试分析结果表明，本文提出的小波分析故障诊断算法相对于传统的频域故障诊断算法而言，能够高效处理故障特征信息，有效提高了故障诊断的可靠性和精度。

图4 降噪后信号时域图

图5 降噪后信号频域图

图6 Hilbert解调频域图