风机机舱罩的参数化缠绕线型设计及其仿真

2020-05-08李世康邓奕苏军艾孝文

机械工程师 2020年4期

李世康，邓奕,2，苏军，艾孝文

(1. 湖南工程学院机械工程学院，湖南湘潭411104; 2. 湘潭复合材料制造装备工程技术研究中心，湖南湘潭411104;3. 湖南江南四棱数控机械有限公司，湖南湘潭411300; 4. 岳阳长岭设备研究所有限公司，湖南岳阳414012)

0 引言

目前，风能是世界上发展速度最快的可再生能源之一，亦是近期内最具有开发前景的能源，其开发潜力已经受到了世界各国的认可[1]。而为了提高风力发电机对风能的利用，需要解决的一个关键问题就是风机零部件的制造问题。因此，对风机零部件制造的相关问题展开研究与优化，对于解决世界能源和环境问题也有着重要的意义。

风机的各零部件中，机舱罩体积较大，装载着风机的齿轮箱、发电机等关键设备，同时也为维护人员提供了必要的操作空间[2]。因此，对其制造方法的研究很有意义。而复合材料质量轻、强度高、抗疲劳、耐腐蚀，纤维缠绕作为复合材料成型中的重要技术，正好适用于制造机舱罩之类的一体成型的大型结构，制造优势明显[3-5]。纤维缠绕是将纤维通过浸胶后，按照设计好的线型规律缠绕到芯模上，然后固化脱模成制品的一种复合材料成型工艺[6-7]。缠绕结构可以通过改变缠绕角等参数来满足不同的力学性能要求。所以，与其他的复合材料成型方法相比，单从对材料性能的利用率来看，纤维缠绕成型就具有不可忽略的优势。而且，机舱罩是一种典型的非圆截面组合体结构，目前对这种结构的缠绕研究还很少。

综上所述，笔者对机舱罩的纤维缠绕技术展开研究，是针对现有制造工艺的不足的一种解决办法，为机舱罩制造提供了一种新的思路，同时也拓展了对非圆截面组合体结构进行缠绕的应用研究。本研究根据纤维缠绕原理搭建的仿真环境可以根据机舱罩芯模的几何尺寸等要求进行相应的工艺设计，能很方便观察到模拟线型，从而找到设计的不足之处，进一步提高设计过程的效率与合理性。

1 机舱罩数学模型的建立

图1为经过简化后的机舱罩结构，该结构基本保持了机舱罩的非圆截面组合体特征。机舱罩芯模主体部分是由一个长方体的4条侧边倒圆角而成；芯模尾部部分的各截面轮廓中，两条侧边长度与主体部分截面轮廓对应两条边的长度成比例，而其余各边长度和圆角大小与主体部分的相同。

建立坐标系如图2所示。

再设参数θ为垂直于z轴的截面上芯模表面的任意一点与x轴正方向的夹角。

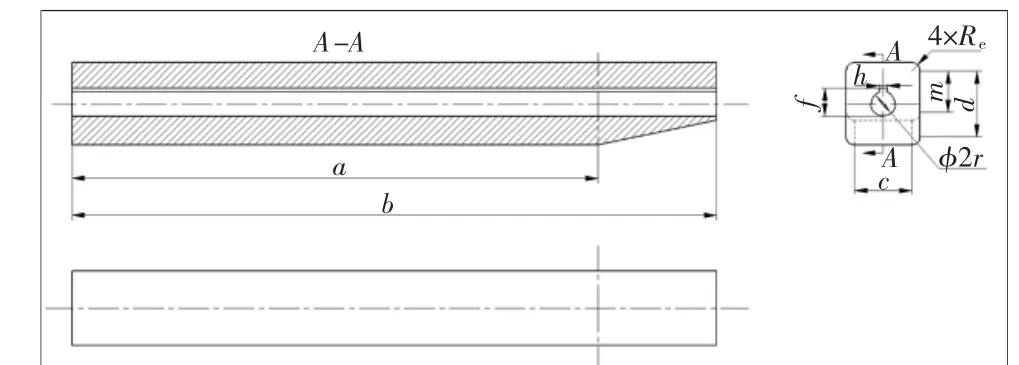
图1 机舱罩结构简图

图2 坐标系的建立

芯模的主体部分由4个圆角面和4个平面组成，圆角面的参数方程为：

其中，对于式(1),θ∈[0°,90°],z∈[0,a];对于式(2),θ∈[90°,180°],z∈[0,a];对于式(3),θ∈[180°,270°],z∈[0,a];对于式(4),θ∈[270°,360°],z∈[0,a]。

各平面的参数方程分别为：

其中，对于式(5), x∈[-c/2,c/2],z∈[0,a];对于式(6),y∈[-d/2,d/2],z∈[0,a];对于式(7),x∈[-c/2,c/2],z∈[0,a];对于式(8),y∈[-d/2,d/2],z∈[0,a]。

则圆角面的参数方程为：

其中，对于式(9),θ∈[0°,90°],z∈(a,b];对于式(10),θ∈[90°,180°],z∈(a,b];对于式(11),θ∈[180°,270°],z∈(a,b];对于式(12),θ∈[270°,360°],z∈(a,b]。

各平面的参数方程分别为：

其中，对于式(13),x∈[-c/2,c/2],z∈(a,b];对于式(14),y∈[d/2-h(z),d/2],z∈(a,b];对于式(15),x∈[-c/2,c/2],z∈(a,b];对于式(16),y∈[d/2-h(z),d/2],z∈(a,b] 。

2 机舱罩的纤维缠绕稳定线型

2.1 机舱罩封头的确定

机舱罩芯模为矩形截面，一般来说，矩形截面芯模的封头有延长型和阶梯轴型两种[8]。由于延长型封头并不缠绕封头端面，不满足机舱罩成型的要求，所以本研究采用的是阶梯轴型封头。

2.2 机舱罩主体表面的测地线方程

机舱罩芯模主体部分的表面由4个圆角面和4个平面组成，应用8个独立方程对其进行描述。由此可知，其主体表面的测地线方程也需要分成8个部分来讨论。而其中平面上的测地线是该面上对应两点的连线，计算过程简单[9]。因此，研究的重点在于计算圆角面的测地线方程。

该面的曲面第一基本量分别为：

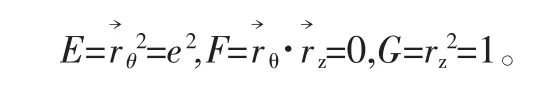
由Liouville公式[10]可得：

于是得到z与θ的微分关系：

测地线缠绕时缠绕角α为定值，故将此微分方程积分即可得到其通解，并可根据初始条件确定其特解。

2.3 机舱罩尾部表面的测地线方程

2.4 机舱罩缠绕过程

综上所述，本研究设计了整个缠绕过程为：首先，纤维从芯模一端的极孔圆周上某点开始，沿封头平面上与极孔圆相切的直线绕过封头。再沿着测地线轨迹绕过机舱罩主体和尾部表面，并绕入芯模的另一端。然后，再返回至尾部和主体表面。最后，回到开始缠绕的一端。如此重复上述过程即可完成机舱罩的缠绕[11]。

3 机舱罩的缠绕线型仿真

3.1 芯模几何模型的建立及其格式转换的方法

首先，在UG软件中创建机舱罩芯模的几何模型，并转存为.stl格式的文件。然后，将.stl格式的文件导入到3Ds Max软件中，并对其坐标进行校正，再转存为FBX格式的文件。然后将FBX格式的文件导入到Unity3D软件中。

3.2 虚拟仿真环境搭建的方法

在Unity3D软件中，首先添加Sphere组件（即：球体组件）并设置其大小，该组件用于展现缠绕落纱点。然后使用C#语言进行编程，用以实现对此前设计的缠绕线型的落纱点坐标的计算，并将求出来的各点坐标代入至Sphere组件的坐标中，从而展现虚拟仿真的效果。

3.3 缠绕线型的仿真实验

以图1的标注为基准，本研究采用了如下芯模尺寸进行线型仿真实验：a=3200 mm, b=3920 mm, c=350 mm, d=400 mm, e=50 mm, r=75 mm, m=234.9 mm（h、f的尺寸并不影响线型设计结果，所以并未列出）。

根据本文中3.1节和3.2节的方法，并综合缠绕工艺要求和展现效果的考虑，本次实验选用了缠绕角α=65°来完成仿真效果。以圆角面r→1(θ,z)的第一段缠绕仿真为例，首先根据该面上第一段的缠绕线型计算出其落纱点坐标，如表1所示。再将该段上各点坐标代入到Sphere组件的坐标中，即可得到落纱点轨迹的虚拟仿真效果，如图3所示。该图中芯模上的白色轨迹即为落纱点轨迹。同理，根据各面上的缠绕线型计算出各自的落纱点坐标，并将这些坐标都代入到Sphere组件的坐标中，即可得到整个机舱罩的缠绕线型仿真效果，如图4所示。

表1 圆角面1(θ, z)上第一段落纱点坐标

编号i xi/mm yi/mm zi/mm 1234 225.0000 223.2963 218.3013 210.3553 200.0000 212.9410 225.0000 235.3553 99.9999 106.1039 112.2079 118.3118 567 200.0000 187.9410 175.0000 243.3013 248.2963 250.0000 124.4158 130.5197 136.6237