焊缝磨抛机器人运动学建模与动力学仿真
2020-05-08葛吉民邓朝晖余卓尔
葛吉民, 邓朝晖, 余卓尔
(1.难加工材料高效精密加工湖南省重点实验室,湖南 湘潭411100;2.湖南科技大学 智能制造研究院,湖南 湘潭411100)
0 引 言
目前结构件焊缝普遍采用人工磨抛,存在着生产效率低、磨抛质量难保证、劳动强度大、成本高、安全性差等问题[1]。虽然市场上出现了焊缝砂带磨抛机,但仍存在柔性差和生产效率不高的问题,因此使用工业机器人作为打磨平台成为快速发展趋势。国内外学者开展了大量研究,Song等[2]搭建了一个机器人打磨平台,基于CAD模型匹配校正打磨工件的姿态误差和位置;张明德等[3]设计了一个机器人砂带打磨系统,并且建立了机器人砂带磨削的数学模型,进行了螺旋桨叶片型面磨抛作业实验。上述初步实现机器人磨抛过程,但其智能化程度仍较低,因此本课题组提出在机器人本体上安装一套焊缝跟踪系统,激光线扫描焊缝,相机抓取轨迹位置信息并控制机器人磨削,实现对结构件焊缝的智能磨抛。
机器人焊缝打磨属于刚性磨削[4],机器人运动、受力过程比较复杂。建立一个准确并满足控制要求的运动学、动力学模型显得尤为重要[5]。目前运动学建模最常用的方法有D-H(参数)法[6-8]和旋量法[9-11]。其D-H法因其简单、方便而应用广泛。动力学建模最常用的方法有:拉格朗日法、牛顿-欧拉法、虚功原理法、凯恩法等。殷志峰等[12]基于Kane-Huston和旋量理论建立了双臂空间机器人动力学模型;张安翻等[13]采用力矩平衡原理和改进的牛顿第二定律构建水下机器人动力学模型;WU等[14]针对并联机器人,利用虚功原理法建立逆动力学方程;WANG等[15]针对3-DOF机器人,基于传统牛顿-欧拉法,提出简化的动力学建模方法;ABDELLATIF等[16]利用Lagrange方程,提出一种建立动力学模型的高效计算方法;STE FAN等[17]以带旋转执行器的机器人为研究对象,创建一种新的动力学分析法(即迭代矩阵法);刘晓等[18]结合虚功率形式达朗贝尔原理建立了机构的耦合动力学方程;GALLARDO等[19]将螺旋理论和虚功原理结合,对机器人进行动力学分析。
本文利用经典成熟的D-H法建立磨抛机器人运动学模型,在此采用简化的牛顿-欧拉法建立其动力学模型,通过Matlab编写程序计算动力学结果。在Simulink和Simmechanics两种环境下联合仿真,并建立一套完整的动力学仿真系统,验证了动力学模型的正确性,为后续智能磨抛机器人的研究奠定了基础。
1 焊缝磨抛机器人运动学分析
1.1 模型参数分析
本文研究的焊缝磨抛机器人三维模型如图1所示,由腰部、大臂、小臂、末端手臂、马达、砂轮组成,此磨抛机器人六个关节都是旋转副,前三个关节确定手腕参考点的位置,后三个关节确定手腕的位姿,关节4、5、6的轴线交于一点。建立必要坐标系,并选取机器人腰关节坐标系为基坐标系,其简化的三维模型如图2所示。
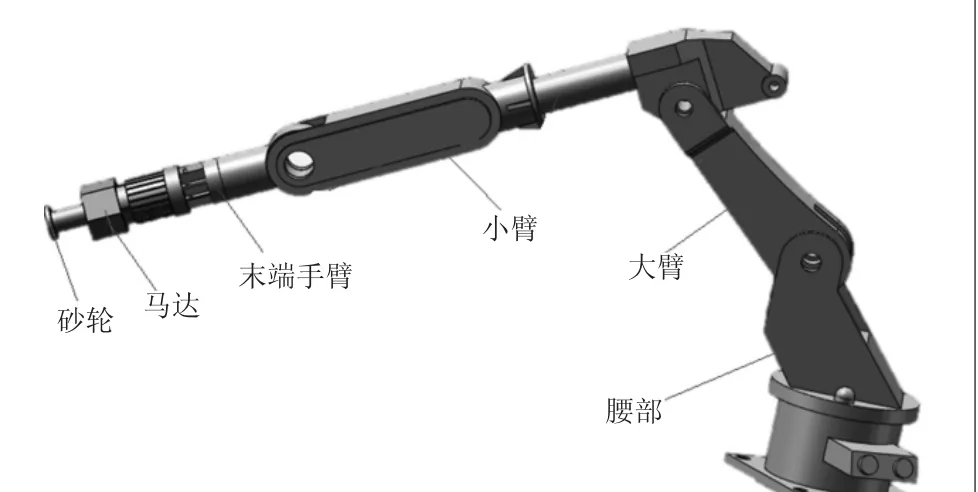
图1 焊缝磨抛机器人三维模型

图2 简化三维模型
1.2 运动学模型建立
1.2.1 正运动学
D-H法建立运动学模型,实质上就是连杆之间的变化矩阵。将这些矩阵依次相乘得到末端砂轮相对于基坐标系的齐次变化矩阵,图2为相邻连杆的坐标变换。

将以上连杆变换矩阵依次相乘得到末端砂轮相对于基坐标系的变换矩阵为


根据上述公式,求得六轴机械臂在相同位姿下可能存在8种关节转角组合,所以往往要根据实际情况选取一种最优的解(行程最短、功率最小、受力最优)。
1.2.3 运动学验证
利用Matlab的Robotics Tool box工具箱,定义磨抛机器人连杆参数如图3所示,当各关节角为[0 π/4 -π 0 π/4 0]时的机器人位姿如图4所示。
利用Matlab的fkine函数,求得在已知各关节角的情况下的变化矩阵为

图3 磨抛机器人连杆参数

图4 磨抛机器人位姿模型

利用Robotices Toolbox[12]中的求逆函数ikine6求得各关节角,其主要命令语句为qz=p560.ikine6s(T),得到的各关节角分别为[0 0.7845 3.1416 0 0.7854 0],[2.6486-3.9270 0.0940 2.5326 0.9743 0.3734 ], 前者与上述正运其中,C=cos θ,S=sin θ。
1.2.2 逆运动学
机器人逆运动学用来描述机器人末端相对于基坐标系的位置关系,即已知末端位姿,求解各关节变量。逆运动学的求解方法最简单的是将依次左乘T的逆矩阵,使两对应元素相等,便可求得各关节变量,求解过程如下:

动学的关节角一致,证明模型的正确性。出现两组关节角也证明了逆运动学的多种转角组合,利用polt函数显示其模型图如图5、图6所示,可以看到有2种姿态。
2 焊缝磨抛机器人动力学建模与仿真
2.1 动力学建模
本文利用简化的牛顿-欧拉法建立磨抛机器人的动力学模型[6],即已知关节角的角位移、角速度、角加速度计算关节力矩。
2.1.1 已知条件
1)多项式插值得到的理想关节 运 动 参数——角位移、加速度、角加速度:
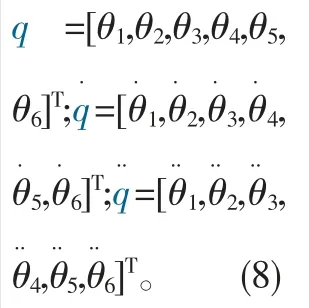

图5 模型右姿态

图6 模型左姿态
2)末端砂轮作用外力f和外力矩和τ。
3)构建的第i个质心在坐标系{i}中的坐标。
4)连杆坐标系{i+1}原点在连杆坐标系{i}的位置矢量P,可以从变化矩阵Ti+1的第四列得到。
5)基座固定,角位移和角速度为0。
2.1.2 旋转关节的速度和加速度传递
连杆i+1的角速度等于连杆i的角速度加上连杆i+1绕关节i+1旋转的角速度,在坐标系{i+1}中表示为

坐标系{i+1}原点线速度大小等于坐标系{i}原点线速度加连杆i转动速度的分量,在坐标系{i+1}中表示为

由式(9)、式(10)进一步推得角加速度和线加速度传递公式:
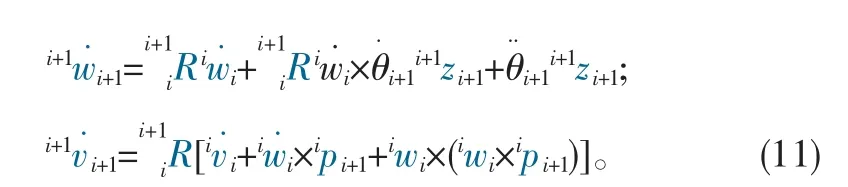
2.1.3 质心的速度和加速度
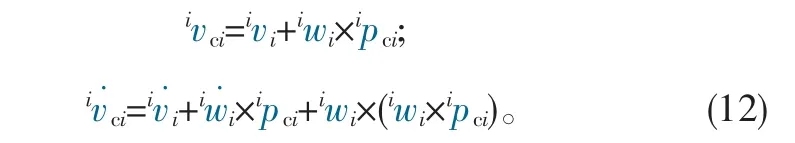
2.1.4 牛顿力平衡方程和欧拉力矩平衡方程

2.1.5 递推的牛顿-欧拉动力学算法
首先向外递推计算各连杆速度、加速度;其次利用牛顿-欧拉方程求得各连杆惯性力和力矩;最后向内递推计算出各关节相互作用力和力矩,乘z分量得到各关节的驱动力矩:

通过上式计算得到所需驱动力和驱动力矩:


2.2 动力学计算
根据上述公式,采用递推的牛顿-欧拉方程,利用Matlab编程求得各关节完成运动所需关节力矩,程序流程如图7所示。
起始位置各关节角为[3.2631,2.0791,0.5992,0,0.4633,0.1215], 终止位置各关节角为[2.3358,2.0791,0.5992,-2.3209, 1.2425,-2.377],使磨抛机器人做直线运动(如图8)。采用多项式插值的方法,用Matlab计算各关节角、关节角速度、关节角加速度,最终通过牛顿-欧拉递推求得在此过程中磨抛机器人各关节驱动力矩如图9所示。
2.3 动力学仿真
在SoildWorks和Simmechanics两种环境下对磨抛机器人进行动力学仿真[20]。
机器人Simmechanics模型图如图10所示;通过from workspace将上述求出的关节角、关节角速度、关节角加速度作为信号输入端求得所需的关节驱动力矩如图11所示。
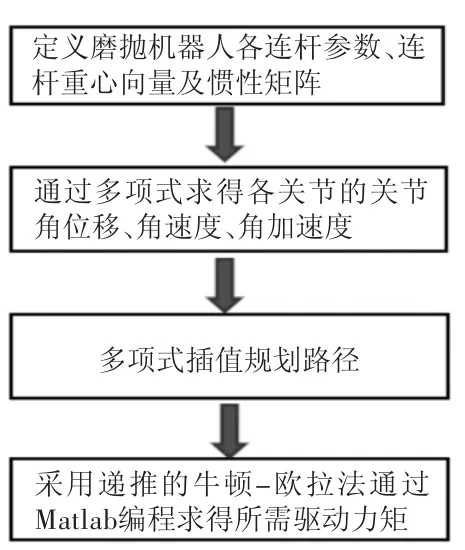
图7 程序流程图

图8 机器人直线运动轨迹

图9 理论计算各关节力矩变化
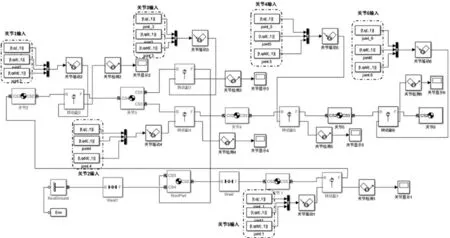
图10 Simmechanics模型
通过理论计算和仿真结果的对比,关节1、2、3、4、5、6 的仿真结果与理论计算结果趋于一致。但其存在一定偏差的原因可能是仿真模型的三维模型图与理论计算使用的磨抛机器人各参数(连杆质量、质心位置等)存在偏差。

图11 仿真计算各关节力矩变化
3 结 论
提出一种快速建立机器人运动学与动力学模型的方法,并通过Matlab编程计算机器人实现直线运动所需的驱动力大小,最终在Simulink和Simmechanics两种环境下联合仿真,利用力矩输入模块、力矩检测模块搭建仿真,并通过scope以示波器的方式输出仿真的结果,仿真结果与理论计算结果大体一致。验证该简化动力学模型的正确性,为后续磨抛机器人进一步动力学及控制研究奠定了基础。
