一般的中性Gauss-Bonnet-AdS黑洞复杂度演化
2020-05-08梁华志张靖仪
梁华志,张靖仪
(广州大学 物理与电子工程学院,广东 广州,510006)
复杂度是量子信息理论中的概念,指的是从一个参考状态到一个目标状态所需要的量子门的最小数目。在量子信息中,量子门指的就是简单操作。2015年Brown等[1]基于全息引力[2-5],提出了复杂度—作用量对偶(Complexity-Action duality,简称CA对偶),他指出d维边界全息状态的量子计算复杂度对偶于(d+1)维Wheeler-DeWitt patch(简称WDW片)的经典作用量。研究黑洞复杂度的问题最终回到了对作用量的计算,这是研究黑洞复杂度的全新方法。应该指出的是在Brown等[1]提出复杂度—作用量对偶之前,Susskind[6]提出了复杂度—长度对偶,Stanford[7]等提出了复杂度—体积对偶,逐步改进后才有了后来的Brown等[1]提出的复杂度—作用量对偶。
CA对偶提出后的短短几年,黑洞复杂度的研究得到了很大发展[8-14]。到目前为此,人们利用CA对偶,得到了Schwarzschild-AdS黑洞和RN-AdS黑洞全时(包含初期和晚期)的复杂度演化的结果[8,12],以及Kerr-AdS黑洞的晚期复杂度演化的结果[9]。与此同时,对于高阶导数引力,特别是Gauss-Bonnet引力和三阶Lovelock引力的复杂度演化也有了很大发展[13-14]。最近Fan[14]等得到了一般高阶导数引力的复杂度演化公式,并利用数值方法对平面的(k=0)中性Gauss-Bonnet-AdS黑洞的复杂度演化进行了详细讨论,特别需要注意的是Fan[14]等对中性Gauss-Bonnet-AdS黑洞复杂度讨论的结果仅局限于视界面几何为平面的情况(k=0)。本文将在Fan等[14]工作的基础上,利用一般高阶导数引力的复杂度演化公式,对一般的(k任意)中性Gauss-Bonnet-AdS黑洞的复杂度演化进行计算,得到一般的中性Gauss-Bonnet-AdS黑洞的复杂度演化公式,不失一般性,我们再利用数值方法,画出平面的(k=0)以及球对称的(k=1)中性Gauss-Bonnet-AdS黑洞的复杂度演化图以及微分图,找出不同视界几何的中性Gauss-Bonnet-AdS黑洞复杂度演化的共同点以及差异,并对结果进行一些讨论。
1 一般的中性Gauss-Bonnet-AdS黑洞复杂度演化公式
复杂度—作用量对偶[1](Complexity-Action duality,简称CA对偶):

其中,dC/dt表示复杂度增长速率,dI/dt表示作用量增长速率,使用自然单位制,普朗克常量ħ=1。一般的中性高阶导数引力AdS黑洞(D维)线元表达式为

一般h(r) ≠f(r),k= 1 ,0,-1分别表示视界面为球面、平面以及双曲抛物面的黑洞。
根据Fan等[14]的结果,一般的中性高阶导数引力AdS黑洞的复杂度增长速率为

其中,Δ为总作用量增长速率的晚期极限。图1为一般的中性双边AdS黑洞WDW片的示意图,rm为WDW片两条过去类光边界交界处的径向坐标。临界时间tc指的是WDW片两条过去类光边界相交的“节点”恰好落在过去奇点上所对应的时间t,t为两侧边界时间之和,即

乌龟坐标r∗(r)定义为

所以r∗(∞) = 0 。一般的中性高阶导数引力AdS黑洞的温度函数

瓦尔德熵函数

D维(D≥5)的一般的中性Gauss-Bonnet-AdS黑洞线元表达式为
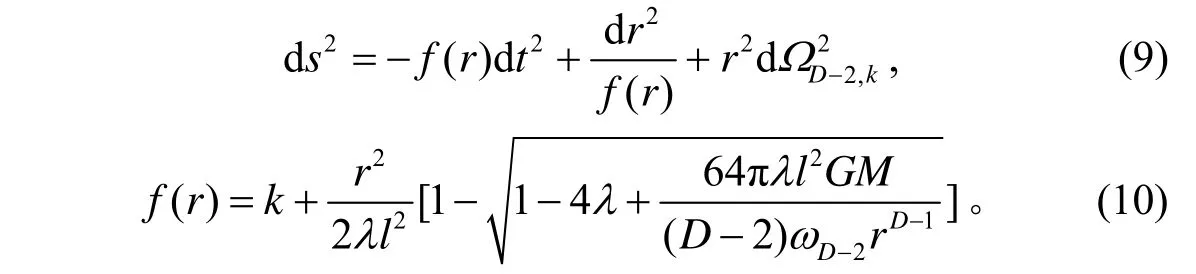
其中,k= 1 ,0,-1分别表示视界面为球面、平面以及双曲抛物面的黑洞,此时w(r)=1,l为AdS半径,M为黑洞质量,ωD-2为和视界面几何相关的余二维的单位体积。λ为耦合常数,它的取值范围为


图1 一般的中性双边AdS黑洞Wheeler-DeWitt patch


可以得到一般的中性Gauss-Bonnet-AdS黑洞总作用量增长速率的晚期极限
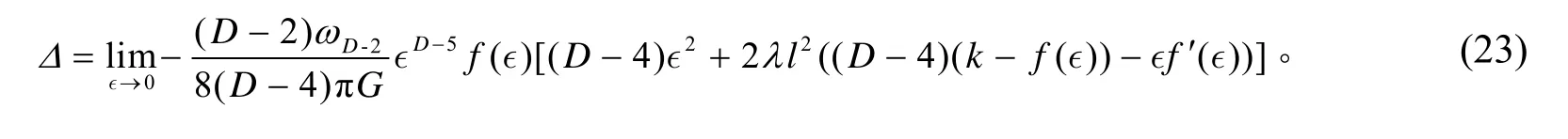
进一步计算,得

不难证明,当k=0时,上述结果和Fan等[14]的文章里的平面的中性Gauss-Bonnet-AdS黑洞的结果是完全一致的。
2 一般的中性Gauss-Bonnet-AdS黑洞复杂度演化图和微分图
为了更直观地看出黑洞复杂度演化的情况,本文利用数值方法画出一般的中性Gauss-Bonnet-AdS黑洞复杂度演化图和微分图。由于乌龟坐标在事件视界处是奇异的,不可能直接用数值方法去解(5)式得到rm随时间t的演化函数再代入(4)式从而得到复杂度增长的函数,和Fan等[14]的方法一样,必须引入新的函数F(r)和H(r)

其中,F(rh) = 2 πT/rh。此时,乌龟坐标可以重新表示为

乌龟坐标的奇异部分已经分离到右边第一项,现在可以很容易得到乌龟坐标的数值解。此时,时间t以及临界时间tc分别为
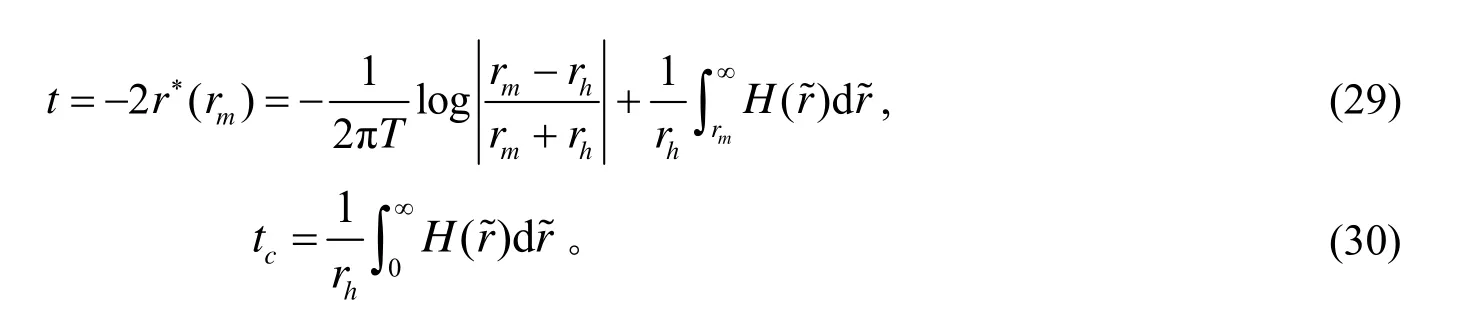
在数值方法里,通常采用无量纲的量,因此采用无量纲的时间≡t/β=Tt,其中β表示热时间,β= 1 /T。此时,无量纲的时间以及临界时间分别为

复杂度增长速率同样需要通过除以晚期极限来无量纲化,即

下面给出一般的中性Gauss-Bonnet-AdS黑洞的复杂度演化的数值分析结果。为不失一般性,选择k= 0(平面黑洞)以及k=1(球对称黑洞)。图2为不同大小的一般的中性Gauss-Bonnet-AdS黑洞的复杂度演化图,图3为对应的复杂度微分图,复杂度微分δC=C(t) -C(tc)通过对dC/dt积分得到。表1和表2分别记录了不同大小的平面(k=0)和球对称(k=1)的中性Gauss-Bonnet-AdS黑洞的无量纲的临界时间。图4为不同耦合常数的一般的中性Gauss-Bonnet-AdS黑洞的复杂度演化图,图5为对应的复杂度微分图,表3和表4分别记录了不同耦合常数的平面(k=0)和球对称(k=1)的中性Gauss-Bonnet-AdS黑洞的无量纲的临界时间。

图2 不同大小的一般的中性Gauss-Bonnet-AdS黑洞的复杂度演化图。选择:λ=0.05,G=α=1,ωD-2=16π。


图3 不同大小的一般的中性Gauss-Bonnet-AdS黑洞的复杂度微分图。选择:λ=0.05,G=α=1,ωD-2=16π。
表1 不同大小的平面的中性Gauss-Bonnet-AdS黑洞无量纲的临界时间(k=0,λ=0.05)

表1 不同大小的平面的中性Gauss-Bonnet-AdS黑洞无量纲的临界时间(k=0,λ=0.05)
images/BZ_34_757_1810_1719_1868.pngD=5 0.379 584 0.379 584 0.379 884 D=6 0.578 743 0.578 743 0.578 743 D=7 0.757 474 0.757 474 0.757 474 D=8 0.926 736 0.926 736 0.926 736
表2 不同大小的球对称的中性Gauss-Bonnet-AdS黑洞无量纲的临界时间(k=1,λ=0.05)
images/BZ_34_757_2239_1719_2297.pngD=5 0.483 888 0.395 163 0.385 353 D=6 0.752 212 0.603 286 0.587 788 D=7 0.996 399 0.790 546 0.769 637 D=8 1.231 620 0.968 409 0.942 043

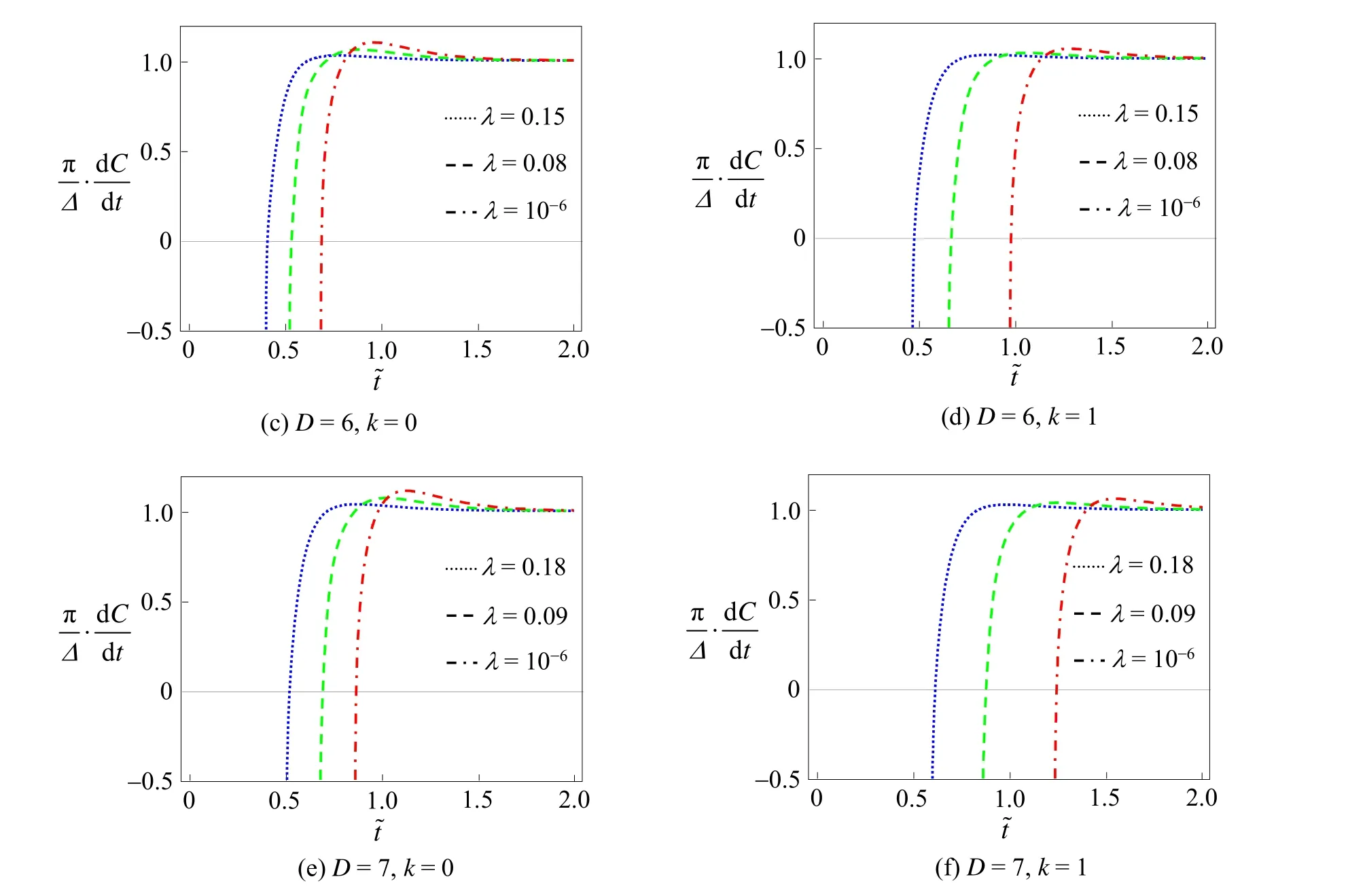
图4 不同耦合常数的一般的中性Gauss-Bonnet-AdS黑洞的复杂度演化图。选择:rh/l=1,G=α=1,ωD-2=16π。


图5 不同耦合常数的一般的中性Gauss-Bonnet-AdS黑洞的复杂度微分图。选择:rh/l=1,G=α=1,ωD-2=16π。
表3 不同耦合常数的平面的中性Gauss-Bonnet-AdS黑洞无量纲的临界时间 (k=0,rh/l=1)
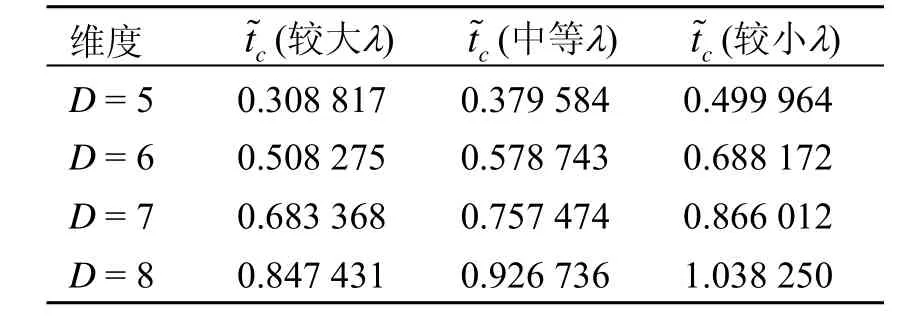
表3 不同耦合常数的平面的中性Gauss-Bonnet-AdS黑洞无量纲的临界时间 (k=0,rh/l=1)
维度 tc ~(较小λ)D=5 0.308 817 0.379 584 0.499 964 D=6 0.508 275 0.578 743 0.688 172 D=7 0.683 368 0.757 474 0.866 012 D=8 0.847 431 0.926 736 1.038 250~(较大λ) tc~(中等λ) tc
表4 不同耦合常数的球对称的中性Gauss-Bonnet-AdS黑洞无量纲的临界时间(k=1,rh/l=1)

表4 不同耦合常数的球对称的中性Gauss-Bonnet-AdS黑洞无量纲的临界时间(k=1,rh/l=1)
~(较小λ)D=5 0.362 820 0.483 888 0.707 060 D=6 0.625 259 0.752 212 0.973 399 D=7 0.855 176 0.996 399 1.231 950 D=8 1.073 700 1.231 620 1.486 990维度 tc~(较大λ) tc~(中等λ) tc
3 结果和讨论
根据数值分析的结果可知,一般的中性Gauss-Bonnet-AdS黑洞的复杂度增长有如下特点:(1)复杂度增长的整体趋势都是先增长到一个局部的极大值,再开始下降,最后趋近于晚期极限;(2)随着维度的增加,不同大小和不同耦合常数的一般的中性Gauss-Bonnet-AdS黑洞的复杂度演化图都会整体往右移,说明一般的中性Gauss-Bonnet-AdS黑洞的无量纲的临界时间随着维度的增大而增大;(3)当k=0时,不同大小的黑洞无量纲的临界时间总是相同的,这和Fan等[14]的文章的分析结果是一致的,而当k=1时,不同大小的黑洞无量纲的临界时间却不再相同,在相同维度下,黑洞越大,无量纲的临界时间越小,而且维度越高,不同大小的黑洞的复杂度演化图越“分散”,说明无量纲的临界时间差别越大;(4)无论是k=0还是k=1,不同耦合常数黑洞无量纲的临界时间随着耦合常数的增加而减小,而且维度越高,不同耦合常数的黑洞之间的无量纲的临界时间的差别越大。
通过比较,可以发现平面的(k=0)和球对称的(k=1)一般的中性Gauss-Bonnet-AdS黑洞的复杂度增长的图像有明显的区别,说明视界几何对黑洞复杂度的增长是有一定影响的。但是不同视界几何的黑洞的复杂度增长的整体规律是一致的,都是增长到一个局部的极大值,再开始下降,最后趋近于晚期极限,这体现了一般的中性Gauss-Bonnet-AdS黑洞的复杂度增长内在的统一性。与此同时,平面的中性Gauss-Bonnet-AdS黑洞也有其特殊性,主要体现在不同大小的平面的中性Gauss-Bonnet-AdS黑洞的无量纲的临界时间都是相同的,而球对称的黑洞没有这样好的性质。
