基于响应面法的挡土墙多失效模式可靠度分析

王成洋，张佳华，肖超，凌涛

基于响应面法的挡土墙多失效模式可靠度分析

王成洋1，张佳华2，肖超3, 4，凌涛5

(1. 中南大学 土木工程学院，湖南 长沙 410075；2. 湖南科技大学 南方煤矿瓦斯与顶板灾害预防控制安全生产重点实验室，煤矿安全开采技术湖南省重点实验室，湖南 湘潭 411201；3. 中建隧道建设有限公司，重庆 401320；4. 中国建筑第五工程局有限公司，湖南 长沙 410004；5. 中铁五局集团 第一工程有限责任公司，湖南 长 沙 410117)

为预防土体发生主动坍塌破坏和被动挤出破坏，研究挡土墙需提供的合理支护力范围，基于极限分析上限法构建挡土墙的主动坍塌和被动挤出2种失效模式，根据虚功率方程求解主动土压力和被动土压力，得到支护力范围。在此基础上，考虑土体参数以及支护力的随机性，建立挡土墙的多失效模式可靠度模型，采用响应面法求解了可靠度，并且引入目标可靠指标获取支护力范围。研究结果表明：与单一失效模式下的结果相比较，基于多失效模式所得到的结果更优。建议采用多失效模式可靠度模型分析挡土墙的稳定性，所得到的支护力范围更合理。

多失效模式；响应面法；主动土压力；被动土压力；可靠指标

挡土墙有主动坍塌和被动挤出2种失效模式。这2种失效模式在实际工程中经常发生，造成巨大的人员伤亡和经济损失。因此，研究挡土墙的稳定性具有重要的科研价值和工程意义[1−2]。目前研究挡土墙稳定性的理论方法一般为极限平衡法和极限分析法。OUYANG等[3]根据极限平衡法计算挡土墙的主动土压力，研究了墙体倾角、土体黏聚力、内摩擦角、回填土的坡度对土体的临界压力系数、土压力的作用点和滑动面形状的影响。Conti等[4]考虑地震效应，采用拟静力法和极限平衡法分析了开挖深度、埋置深度、土体强度等参数对挡土墙稳定性的影响。Rajesh等[5]采用改进的拟动力法和极限平衡法求解了非竖向刚性挡土墙被动土压力的解析解。XU等[6]采用极限平衡法评估静态条件下刚性挡土墙后黏性回填土的应力分布。赵国等[7]根据极限平衡法建立了挡土墙被动土压力的泛函极值变分模型，通过拉格朗日乘子将等周变分模型转化为含有2个自变量的泛函极值模型，其计算结果与库仑土压力解一致。此外，一些学者采用极限分析法研究挡土墙的稳定性。如：李泽等[8]采用极限分析下限法构建了静力许可的应力场，求解了挡土墙的极限承载力，并通过算例验证了结果的正确性。HUANG等[9]采用极限分析上限法建立了重力式挡土墙的地震旋转稳定性理论模型，该模型考虑了挡土墙高度、形状、土体容重以及墙土界面摩擦角的影响。高昂等[10]采用极限分析上限法构建了加筋土挡墙的破坏模式，并且分析了其抗震性能。Karkanaki等[11]采用极限分析上限法和拟静力法研究挡土墙的稳定性，并且求解了地震加速度系数的临界值。王作伟等[12]运用拟静力法和极限分析上限法求解地震作用下挡土墙的主动土压力，并验证了结果的正确性。以上文献均只研究了挡土墙的单一失效模式，即主动坍塌失效模式或被动挤出失效模式。本文同时考虑挡土墙的这2种失效模式，采用极限分析上限法和响应面法研究挡土墙的稳定性，并且给出满足安全等级的合理支护力范围，为类似工程提供参考。

1 挡土墙失效模式

挡土墙所提供的支护力小于主动土压力，墙后土体极易发生主动破坏，向挡土墙方向坍塌；挡土墙所提供的支护力大于被动土压力，墙后土体又极易发生被动破坏，向远离挡土墙方向挤出[13−14]。因此，本文基于挡土墙墙后土体的破坏特征，结合已有研究成果[15−16]，采用极限分析上限法构建挡土墙的主动与被动失效模式，如图1和图2所示。挡土墙高度或土体高度为，墙背竖直倾角为1，墙后土体破裂面为，破裂角为，土体水平倾角为2，地表荷载为，墙背与土体之间的外摩擦角为，主动土压力为E，被动土压力为E。0，01和1为速度场中各间断线的速度，满足闭合关系。

由图1和图2可得：

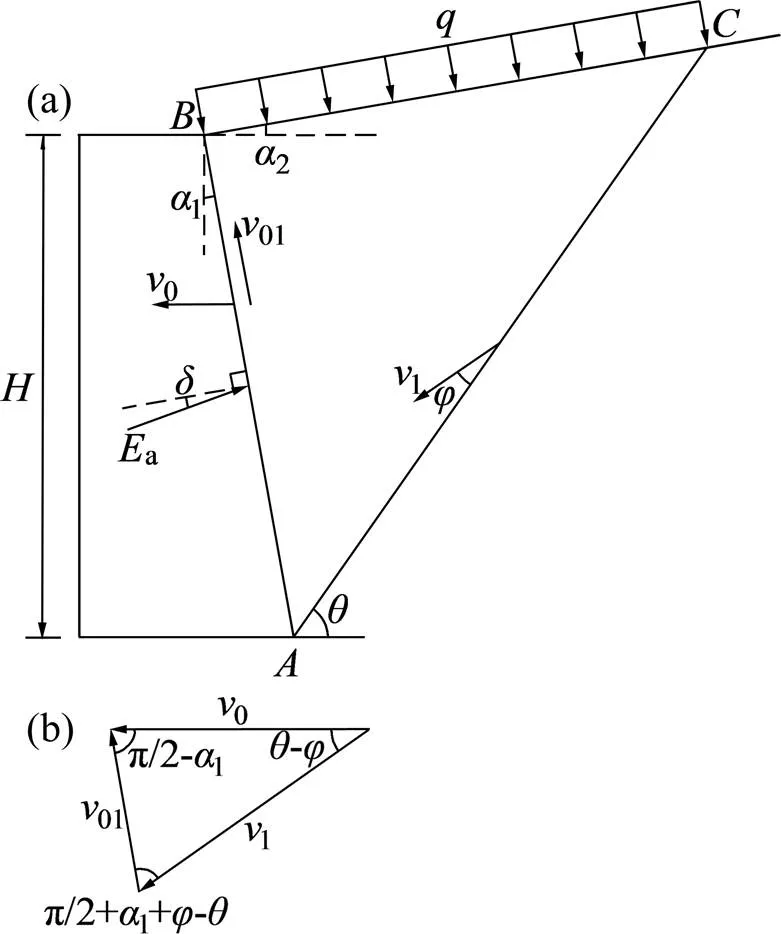
(a) 破坏机制；(b) 速度场

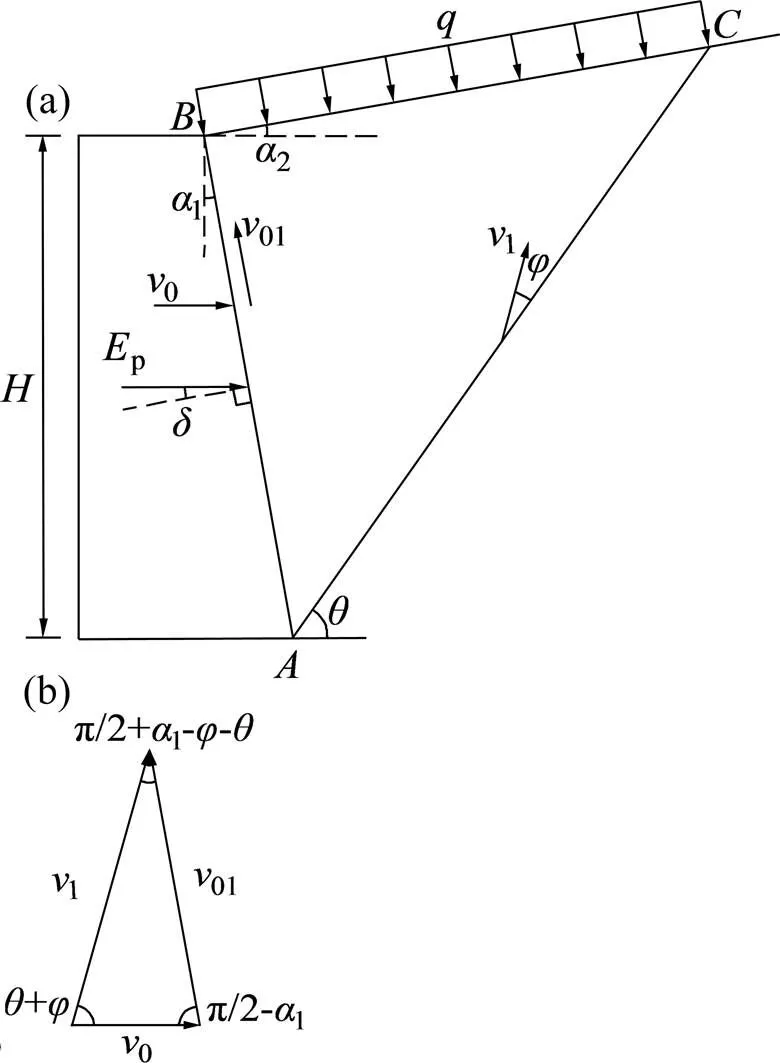
(a) 破坏机制；(b) 速度场

2 土压力计算

2.1 假设条件

在计算时作如下假设：1) 挡土墙主动与被动失效模式简化为二维平面应变问题分析；2) 破坏体在滑动过程中体积不变，能量耗散仅发生在速度间断线上。

2.2 主动土压力

2.2.1 速度

根据图1(b)可得主动失效模式各速度：

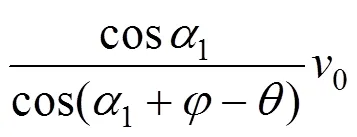
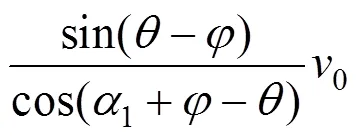
2.2.2 外力功率和内能耗散率

在图1(a)破坏机制中，外力功率包括土体重力功率、地表荷载功率和主动土压力功率。内能耗散仅发生在速度间断线上。

土体重力功率为：

地表荷载功率为：

主动土压力功率为：

内能耗散率为：

2.2.3 优化求解

根据外力功率等于内能耗散率建立虚功率 方程：

根据虚功率方程可推导出主动土压力的解 析解：

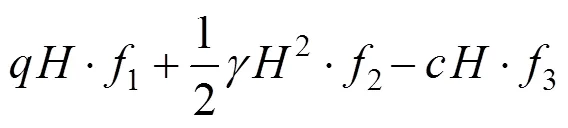
约束条件为：

在式(16)约束条件下，采用Matlab软件中穷举法可得到式(12)主动土压力最优解。

2.3 被动土压力

2.3.1 速度

根据图2(b)可得被动失效模式各速度：

2.3.2 外力功率和内能耗散率

在图2(a)破坏机制中，外力功率包括土体重力功率、地表荷载功率和被动土压力功率。内能耗散仅发生在速度间断线上。

土体重力功率为：

地表荷载功率为：

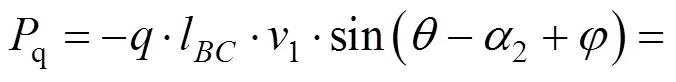
被动土压力功率为：

内能耗散率为：

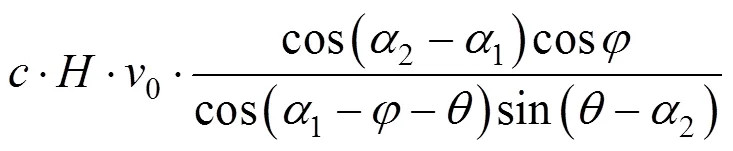
2.3.3 优化求解

根据外力功率等于内能耗散率建立虚功率 方程：

根据虚功率方程可推导出被动土压力的解 析解：

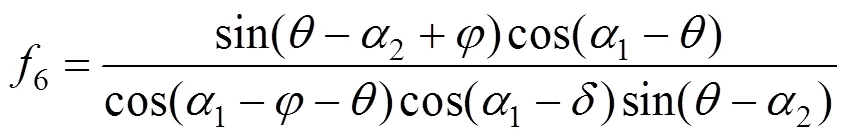
约束条件为：

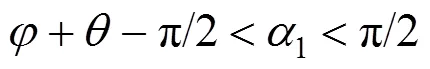
在式(28)约束条件下，采用Matlab软件中穷举法可得到式(24)被动土压力最优解。

3 多失效模式可靠度模型

基于图1和图2中挡土墙主动与被动失效模式，采用极限分析上限法分别求解主动土压力a和被动土压力p。假定挡土墙对墙后土体所提供的支护力为，墙后土体发生主动坍塌破坏或被动挤出破坏的极限状态方程分别为：

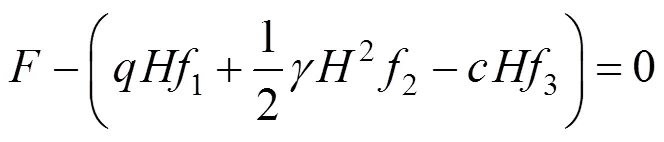
考虑单一失效模式，挡土墙墙后土体不发生主动坍塌破坏或被动挤出破坏，其可靠度模型分 别为：

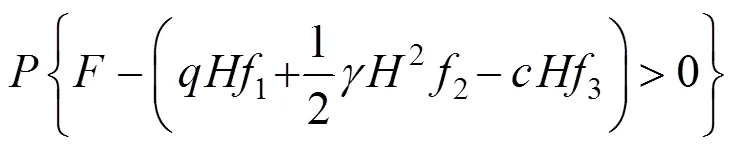
考虑多失效模式，挡土墙墙后土体既不发生主动坍塌破坏也不发生被动挤出破坏，其可靠度模型为：

失效概率为：

可靠指标为：

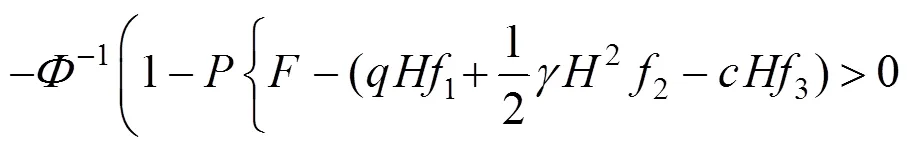
4 对比

表1为土体参数和支护力的统计特征，其余参数不考虑随机性，其值分别为：土体高度=8 m，地表荷载=20 kN/m2，墙背竖直倾角1=10°，土体水平倾角2=10°，外摩擦角=0。基于挡土墙单一失效模式可靠度模型与多失效模式可靠度模型，采用响应面法分别计算了失效概率和可靠指标，如图3所示。以图3(b)中的可靠指标为例进行分析，随着支护力均值F递增，单一主动失效模式下挡土墙的可靠指标非线性递增，单一被动失效模式下挡土墙的可靠指标非线性递减；多失效模式下挡土墙的可靠指标先非线性递增，然后非线性递减，且与单一失效模式曲线基本重合。由此可见，多失效模式同时考虑了单一主动和单一被动2种失效模式，且计算结果高度吻合，则验证了多失效模式结果的正确性以及其可靠度模型的优越性。

表1 土体参数及支护力的统计特征Ⅰ

(a) 失效概率；(b) 可靠指标

5 结果分析

5.1 主动土压力与被动土压力

不考虑土体参数及支护力的随机性，其参数值分别为：土体高度=8 m，土体重度=18 kN/m3，黏聚力=15 kPa，内摩擦角=20°，地表荷载=20 kN/m2，墙背竖直倾角1=10°，土体水平倾角2=10°，外摩擦角=0。采用极限分析上限法求解挡土墙的主动土压力和被动土压力。如图4所示，随着土体高度增大，主动土压力a和被动土压力E均非线性增大；随着地表荷载增大，主动土压力a和被动土压力E均线性增大。这表明土体高度和地表荷载越大，挡土墙越容易发生主动坍塌破坏；反之，土体高度和地表荷载越小，挡土墙越容易发生被动挤出破坏。随着黏聚力增大，主动土压力a线性减小，被动土压力E线性增大；随着内摩擦角增大，主动土压力a非线性减小，被动土压力p非线性增大。这表明表征土体抗剪强度的黏聚力和内摩擦角越小，土体越不稳定，挡土墙就越容易发生主动坍塌破坏或被动挤出破坏。随着墙背竖直倾角1增大，主动土压力a非线性增大，被动土压力p非线性减小。这表明墙背竖直倾角1增大不利于挡土墙的稳定性，即挡土墙更容易发生主动坍塌破坏或被动挤出破坏。随着土体水平倾角2增大，主动土压力a和被动土压力p均非线性增大。这表明土体水平倾角2增大更容易引起挡土墙发生主动坍塌破坏，反之则更容易引起挡土墙发生被动挤出破坏。

(a) H-q-Ea；(b) H-q-Ep；(c) c-φ-Ea；(d) c-φ-Ep；(e) α1-α2-Ea；(f) α1-α2-Ep

5.2 可靠指标与支护力范围

考虑土体参数及支护力的随机性，如表2所示，其余参数值分别为：土体高度=8 m，地表荷载=20 kN/m2，墙背竖直倾角1=10°，土体水平倾角2=10°，外摩擦角=0。基于挡土墙的多失效模式可靠度模型，采用响应面法求解了可靠指标。如图5所示，随着支护力均值F递增，挡土墙的可靠指标先非线性增大，达到最高点后再非线性减小。这表明支护力增大初期，此时挡土墙以主动坍塌破坏为主，其失效概率减小，可靠指标增大，而达到最高点后，支护力继续增大，此时挡土墙以被动挤出破坏为主，其失效概率增大，可靠指标减小。为了确保挡土墙的稳定性，以安全等级1即目标可靠指标=4.2作为设计要求，可以得到挡土墙合理的支护力范围，如表3所示，以=20°为例，采用极限分析上限法所得到挡土墙的主动土压力为276 kN/m，被动土压力为2 013 kN/m，那么不考虑土体参数及支护力的随机性，采用定值法所得到挡土墙的支护力范围为276~2 013 kN/m。但是考虑土体参数及支护力的随机性，基于多失效模式可靠度模型采用响应面法所得到挡土墙的支护力范围为845~ 1 088 kN/m，则明显缩小了支护力范围，从而显著降低了挡土墙的失效概率，增大了挡土墙的可靠 指标。

(a) 不同H；(b) 不同q；(c) 不同c；(d) 不同φ；(e) 不同α1；(f) 不同α2

表2 土体参数及支护力的统计特征Ⅱ

表3 基于多失效模式可靠度模型的挡土墙支护力范围

6 结论

1) 采用极限分析上限法构建挡土墙的主动坍塌失效模式和被动挤出失效模式，求解挡土墙的主动土压力和被动土压力。通过参数分析可得，土体高度，土体水平倾角2以及地表荷载越大，挡土墙越容易发生主动坍塌破坏，反之挡土墙容易发生被动挤出破坏。表征土体抗剪强度的黏聚力和内摩擦角越小，土体越不稳定，挡土墙就越容易发生主动坍塌破坏或被动挤出破坏。墙背竖直倾角1增大不利于挡土墙的稳定性，建议无特殊地质条件或设计要求优先考虑垂直式墙背。

2) 基于挡土墙的多失效模式可靠度模型，采用响应面法求解挡土墙的可靠指标，并且得到挡土墙满足安全等级1(目标可靠指标=4.2)的支护力范围。该结果明显缩小了极限分析上限法所得到的支护力范围，显著降低了挡土墙的失效概率，提高了挡土墙的可靠度。针对挡土墙的支护设计，建议采用定值方法和可靠度方法相结合，建立挡土墙的多失效模式可靠度分析模型，本文方法可提供理论 参考。

[1] 龙建辉, 焦姗, 王晓娅. 考虑摩擦损耗的加筋挡土墙临界高度研究[J]. 土木工程学报, 2018, 51(1): 124−128. LONG Jianhui, JIAO Shan, WANG Xiaoya. Critical height research of reinforced retaining wall considering the friction loss[J]. China Civil Engineering Journal, 2018, 51(1): 124−128.

[2] 杨山奇, 卢坤林, 史克宝, 等. 刚性挡土墙后三维被动滑裂面的模型试验[J]. 岩土力学, 2018, 39(9): 3303− 3312. YANG Shanqi, LU Kunlin, SHI Kebao, et al. Model tests on 3D slip surface of passive failure behind a rigid retaining wall[J]. Rock and Soil Mechanics, 2018, 39(9): 3303−3312.

[3] OUYANG Chaojun, XU Qiang, HE Siming, et al. A generalized limit equilibrium method for the solution of active earth pressure on a retaining wall[J]. Journal of Mountain Science, 2013, 10(6): 1018−1027.

[4] Conti R, Viggiani G M B. A new limit equilibrium method for the pseudostatic design of embedded cantilevered retaining walls[J]. Soil Dynamics and Earthquake Engineering, 2013, 50: 143−150.

[5] Rajesh B G, Choudhury D. Seismic passive earth resistance in submerged soils using modified pseudo-dynamic method with curved rupture surface[J]. Marine Georesources and Geotechnology, 2017, 35(7): 930−938.

[6] XU S Y, Kannangara K K P M, Taciroglu E. Analysis of the stress distribution across a retaining wall backfill[J]. Computers and Geotechnics, 2018, 103: 13−25.

[7] 赵国, 陈建功. 挡土墙上被动土压力的变分求解方法[J]. 土木与环境工程学报(中英文), 2019, 41(2): 29−35. ZHAO Guo, CHEN Jiangong. Variational method for computation of passive earth on retaining wall[J]. Journal of Civil and Enviromental Engineering, 2019, 41(2): 29−35.

[8] 李泽, 刘毅, 周宇, 等. 基于混合离散的砌石挡土墙边坡极限承载力下限分析[J]. 岩土力学, 2018, 39(3): 1100−1108, 1129. LI Ze, LIU Yi, ZHOU Yu, et al. Lower bound analysis of ultimate bearing capacity of stone masonry retaining wall slope using mixed numerical discretisation[J]. Rock and Soil Mechanics, 2018, 39(3): 1100−1108, 1129.

[9] HUANG D, LIU J. Upper-bound limit analysis on seismic rotational stability of retaining wall[J]. KSCE Journal of Civil Engineering, 2016, 20(7): 2664−2669.

[10] 高昂, 张孟喜. 直立式加筋土挡墙基于极限分析的抗震性能研究[J]. 地震工程学报, 2019, 41(2): 313−318, 384. GAO Ang, ZHANG Mengxi. Seismic performance of vertically reinforced earth-retaining walls based on limit analysis[J]. China Earthquake Engineering Journal, 2019, 41(2): 313−318, 384.

[11] Karkanaki A R, Ganjian N, Askari F. Pseudo-static analysis of cantilever retaining walls using upper bound limit analysis approach[J]. Journal of Central South University, 2019, 26(1): 241−255.

[12] 王作伟, 杨小礼. 水平地震力对非线性主动土压力上限解的影响[J]. 矿业工程研究, 2009, 24(3): 23−26. WANG Zuowei, YANG Xiaoli. Upper bound solution of active earth pressure considering horizontal earthquake and nonlinearity[J]. Mineral Engineering Research, 2009, 24(3): 23−26.

[13] Pain A, Choudhury D, Bhattacharyya S K. Seismic rotational stability of gravity retaining walls by modified pseudo-dynamic method[J]. Soil Dynamics and Earthquake Engineering, 2017, 94: 244−253.

[14] LI X P, SU L J, WU Y, et al. Seismic stability of gravity retaining walls under combined horizontal and vertical accelerations[J]. Geotechnical and Geological Engineering, 2015, 33(1): 161−166.

[15] ZHANG D B, JIANG Y, YANG X L. Estimation of 3D active earth pressure under nonlinear strength condition[J]. Geomechanics and Engineering, 2019, 17(6): 515−525.

[16] 刘洋, 于鹏强. 刚性挡土墙平移模式的土拱形状与主动土压力分析[J]. 岩土力学, 2019, 40(2): 506−516, 528. LIU Yang, YU Pengqiang. Analysis of soil arch and active earth pressure on translating rigid retaining walls[J]. Rock and Soil Mechanics, 2019, 40(2): 506−516, 528.

Reliability analysis of multi-failure mode for retaining wall based on response surface method

WANG Chengyang1, ZHANG Jiahua2, XIAO Chao3, 4, LING Tao5

(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. Work Safety Key Lab on Prevention and Control of Gas and Roof Disasters for Southern Coal Mines,Hunan Provincial Key Laboratory of Safe Mining Techniques of Coal Mines, Hunan University of Science and Technology, Xiangtan 411201, China; 3. China Construction Tunnel Corp., Ltd, Chongqing 401320, China; 4. China Construction Fifth Engineering Division Corp., Ltd, Changsha 410004, China;5. The First Engineering Co. Ltd. of China Railway Wuju Group, Changsha 410117, China)

In order to avoid the active collapse and passive extrusion failure of soil masses, the reasonable range of supporting force of retaining walls was determined. These active collapse and passive extrusion failure modes of retaining walls were constructed based on the upper bound method of limit analysis. The active and passive earth pressure was solved according to the virtual power equation. And then the range of supporting force was obtained. On this basis, the multi-failure reliability model of retaining walls was established considering the randomness of soil parameters and supporting force. The reliability of retaining walls was solved by the response surface method. Moreover, the target reliability index was introduced to acquire the range of supporting force. The results show that the result from the multi-failure mode is better than which of single failure mode. It is suggested to adopt the multi-failure reliability model to analyze the stability of retaining walls, and the range of supporting force will be more reasonable.

multi-failure mode; response surface method; active earth pressure; passive earth pressure; reliability index

TU43

A

1672 − 7029(2020)04 − 0882 − 09

10.19713/j.cnki.43−1423/u.T20190560

2019−06−21

国家自然科学基金资助项目(51804113)

张佳华(1983−)，男，湖北天门人，讲师，博士，从事隧道与地下工程方面研究；E−mail：1010090@hnust.edu.cn

(编辑 涂鹏)