高铁路基在振动荷载下的空间动态响应特性试验研究
2020-05-07吴龙梁于琦江辉煌向卫国高明显闫晓夏
吴龙梁,于琦,江辉煌, ,向卫国,高明显,闫晓夏
高铁路基在振动荷载下的空间动态响应特性试验研究
吴龙梁1,于琦2,江辉煌1, 3,向卫国1,高明显3,闫晓夏3
(1. 中国铁道科学研究院,北京 100081;2. 深圳市建筑工务署,广东 深圳 518031;3. 中国铁道科学研究院 深圳研究设计院,广东 深圳 518000)
为从空间的角度探讨振动荷载下路基的动力响应特性,开展基于振动速度和加速度的现场激振响应试验,得到路基内部水平和竖向动力响应分量沿不同方向的衰减规律。研究结果表明:响应加速度和响应速度沿深度方向和水平方向均呈指数衰减,沿深度方向的衰减相比水平方向更为显著,深度方向衰减系数为水平方向衰减系数的2.5~3倍,并且距离激振点越远衰减越缓慢;响应速度和加速度的竖向分量幅值约为水平分量幅值的2倍,水平分量沿水平方向的衰减速度约为竖向分量的1.5~1.9倍,水平分量沿深度方向的衰减速度约为竖向分量的0.9~1.0倍;进行滤波处理后的响应加速度与响应速度的变化规律相近。加速度对外界激励的响应相比速度更为敏感,能够较好反映出衰减规律的细微变化。
高铁路基;动力响应;加速度;速度;土动力互易性

高铁路基的性能关系到路线的平顺性与运行安全,高铁路基的动力响应特性是反映和评判其性能的关键依据[1]。研究振动荷载下高铁路基的动力响应特性受到了业界的广泛关注且具有重要的现实意义。试验研究具有较强的针对性和可靠性,能够直观、真实地反映实际情况,是研究路基动力响应问题的重要手段。Ishikawai等[2]开展了轨道路基模型试验,研究了模拟移动荷载作用下路基内部的动应力分布规律和累积沉降规律。Shaer等[3]通过特定的加载器模拟列车荷载的移动效应,研究了不同加载振次下路基的累计沉降变化规律。Indraratna等[4]采用自制的加载设备开展了铁路路基动力响应模型试验,研究了路基的应力/应变传递和衰减规律。牛婷婷等[5]基于大比例尺模型试验,研究了列车荷载作用下路基响应速度幅值沿深度方向的衰减规律和横向振动传播规律。陈善雄等[6]开展了现场激振试验,探讨了高铁路基动应力和加速度沿深度方向的变化规律。目前,路基的累计变形沉降[2−3, 7−9]、动位移[9−10]、动应力[2, 4, 6, 10−11]、振动速度[5]和振动加速度[6, 12−13]的变化规律是高铁路基动力响应主要研究内容。其中,基于振动加速度的研究相对较多,基于振动速度的研究较少。路基在车辆振动荷载下的振动速度多为mm/s量级,而振动加速度可以达到m/s2的量级,振动加速度因更具可测性而在试验研究中得到了广泛采用。而另一方面,加速度传感器对激励十分敏感,容易受到外部噪音干扰而产生误差。速度传感器则受频率变化的影响较小,具有良好的稳定性。因此,两者的适用性存在一些不确定性,有必要针对路基动力响应加速度和响应速度进行对比研究。另外,目前关于路基动力响应规律的研究多为沿单一方向的规律研究,尤其是响应物理量的竖向分量沿深度方向的变化规律,而以空间的角度探讨高铁路基内部的动力响应规律的报道较为少见。实际上,路基的动力响应是一个空间问题,振动沿水平方向的作用不容忽视。动力响应物理量沿水平方向的变化规律以及其水平分量的变化规律尚需进一步研究与探讨。为此,本文通过开展振动荷载下高铁路基动力响应现场试验,研究路基内部竖向/水平响应加速度和响应速度沿不同方向的变化规律,以期从空间的角度描述路基的动态响应特性,为高铁路基的设计和质量评估提供依据和参考。
1 现场试验
本次试验在赣深高铁广东段某过渡路基基床处进行。现场试验时路基处于施工阶段,未能采用实际运行时的激振荷载。既有研究表明[5, 14−16],等速列车对均匀路基的作用通常为“M”型周期荷载,可采用振动频率和振动强度相近的简谐振动荷载进行等效替代。因而本试验采用小型振动压路机在压实后的路基面上施加简谐振动荷载以近似模拟动车对路基的振动作用。通过建立动态测试系统采集路基内部的振动数据,以路基不同深度/水平距离处的响应加速度和响应速度作为研究对象,研究路基响应加速度和响应速度的传递与衰减规律、路基动力响应沿深度方向与沿线路方向的变化规律以及动力响应量沿深度方向的竖向分量与沿线路方向的水平分量的变化规律。
1.1 试验方案
根据土体Green函数的互易性[17],激振点与受振点空间位置互换时,路基响应结果保持不变。为增强试验的灵活性和可操作性,减少预埋过多传感器而引起的误差以及传感器失效等风险问题,本试验将振源固定不动时路基内部不同位置处的振动响应问题转换成受振点固定不动而振源分别在不同位置处振动的问题。试验时,在沿线路方向的中轴线0.55 m标高处相间埋设加速度和速度传感器,传感器埋设间隔为1 m。速度传感器共布设2个,依次编号为01号和02号。其中,01号测试竖向速度响应数据,02号测试水平速度响应数据。加速度传感器共布设4个,依次编号为03号,04号,05号和06号。其中,03号测试水平加速度响应数据,04号测试竖向加速度响应数据,05号为校对用传感器,06号为备用传感器。按不同层厚分层压实回填并依次采集不同水平位置处的振动响应数据。回填层厚依次为15,10,20,15和15 cm,受振点与激振点的水平距离为0~6 m,激振点的水平间距为1 m,激振点和传感器布置如图1所示。

单位:cm
1.2 试验测试系统
试验测试系统主要由路基基床、试验加载系统、传感器和数据采集系统4部分组成。路基基床采用不均匀系数为6.4,曲率系数为1.83,最大干密度为2.03 g/cm3的B组填料分层填筑,填筑压实过程与数据采集交叉进行。试验填筑前进行填料预碾压测试,确定本试验条件下路基的最大压实度为0.97,试验碾压遍数为6遍,填料虚铺厚度系数约为1.15。试验加载系统采用可稳定输出正弦波形的YZF3.0型振动压路机,其工作质量为3 000 kg,激振频率为30 Hz,激振力为30 kN。振动测试采用的竖向加速度传感器为INV9823型传感器,测试量程为25,测试频率范围为0.5~4 000 Hz,测试分辨率为250 μm/s2。水平加速度传感器为941B型传感器,测试量程为20,测试频率范围为0.25~80 Hz,测试分辨率为5 μm/s2。速度传感器为941B型传感器,测试量程为0.6 m/s,测试频率范围为0.17~100 Hz,测试分辨率为1.6 μm/s。传感器如图2所示。传感器现场埋设时加盖自制防护罩防护,接线穿过厚壁PVC套管防护,如图3所示。数据采集系统采用INV3062C型采集仪,通过与安装有DASP V11动态信号采集分析系统的笔记本电脑相连,实时获取响应数据并储存于电脑硬盘。

图2 传感器

图3 传感器现场埋设
1.3 试验数据采集
试验中路基共分为5个测试层,待各测试层回填压实至最大压实度后再进行振动测试。压实度检测采用灌砂法,若低于控制标准则增加碾压遍数,并重新检测压实度,直至满足压实要求后再进行振动测试。为保障采集数据的准确性和可靠性,试验前需对传感器进行标定处理。振动压路机的振动轮依次在各层激振点处稳定振动,振动持时不少于60 s,同时采集振动响应数据。各测试层重复测试2次以上,若存在测试波形异常情况,则重新测试直至连续2次的测试结果一致为止。
2 试验结果及分析
2.1 动态响应测试结果
试验过程中,采集到激振点在不同位置时各受振点的加速度和速度响应数据。根据土体Green函数的空间互易性,将某一受振点的各组响应数据依次对应等效为激振点固定不动时沿线路方向剖面不同位置处的动力响应值,从而得到路基内部的动力响应结果。为减小外部噪声干扰,对测试结果进行低通滤波处理(截止频率取200 Hz),同时对振动数据进行傅里叶变换以分析振动频谱并剔除异常数据。部分处理后的测试结果如图4所示。
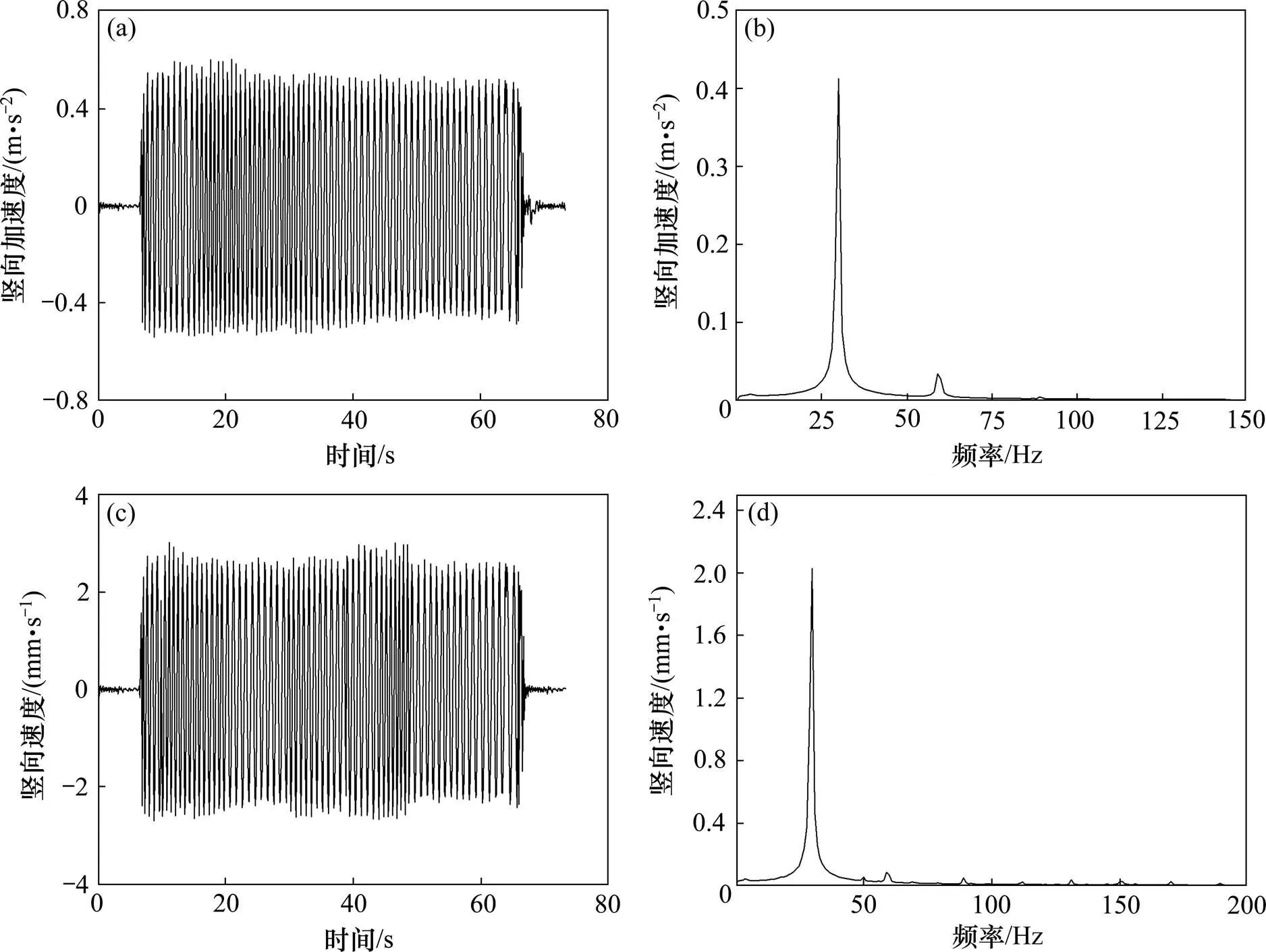
(a) 竖向加速度时域图(04号,h=0.15 m,L=4 m);(b) 竖向加速度频谱图(04号,h=0.15 m,L=4 m);(c) 竖向速度时域图(01号,h=0.15 m,L=4 m);(d)竖向速度频谱图(01号,h=0.15 m,L=4 m)
由图4可知,采集到的响应加速度信号和响应速度信号近似呈周期性波动,响应基频和谐频趋于离散分布。说明在填料单一、均匀的情况下,路基动力响应信号与激振信号相接近。响应信号的基频均为29 Hz,略小于振动压路机的激振频率30 Hz,表明了测试结果是有效的。
2.2 动态响应的空间规律
为研究路基动力响应特性,通过拟合不同位置处的响应幅值,得到了如图5和图6所示的速度、加速度沿水平方向和深度方向的衰减规律。采用的拟合函数如式(1)所示:
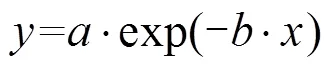
式中:为衰减拟合系数,表示衰减的初始状态;为衰减系数,表征衰减的程度。
(a) 竖向加速度;(b) 水平加速度;(c) 竖向速度;(d) 水平速度
图5 水平方向衰减规律
Fig. 5 Horizontal attenuation law

(a) 竖向加速度;(b) 水平加速度;(c) 竖向速度;(d) 水平速度
由图5和图6可知,函数拟合的相关性系数均在0.9以上,表明函数拟合的效果良好,采用式(1)能够较好描述路基动力响应变化特性。由拟合结果可知,路基中轴剖面加速度和速度沿水平方向和深度方向均呈现指数衰减规律。响应加速度、速度的竖向分量和水平分量沿深度方向和沿水平方向的衰减规律基本一致,竖向分量幅值约为水平分量幅值的2倍,表明路基的动力响应主要体现在竖向分量上,但水平分量不容忽略。在水平方向2 m和深度方向0.45 m范围内加速度和速度衰减迅速,此范围外的衰减缓慢并逐渐趋近于0,表明路基的动力响应区域是有限的。
为对比研究不同位置处的空间衰减规律,分别以各深度位置处的响应幅值的最大值为归一化基准,通过式(1)进行拟合得到各响应物理量沿水平方向相对的变化规律,同理得到沿深度方向相对的变化规律,分别如图7和图8所示。
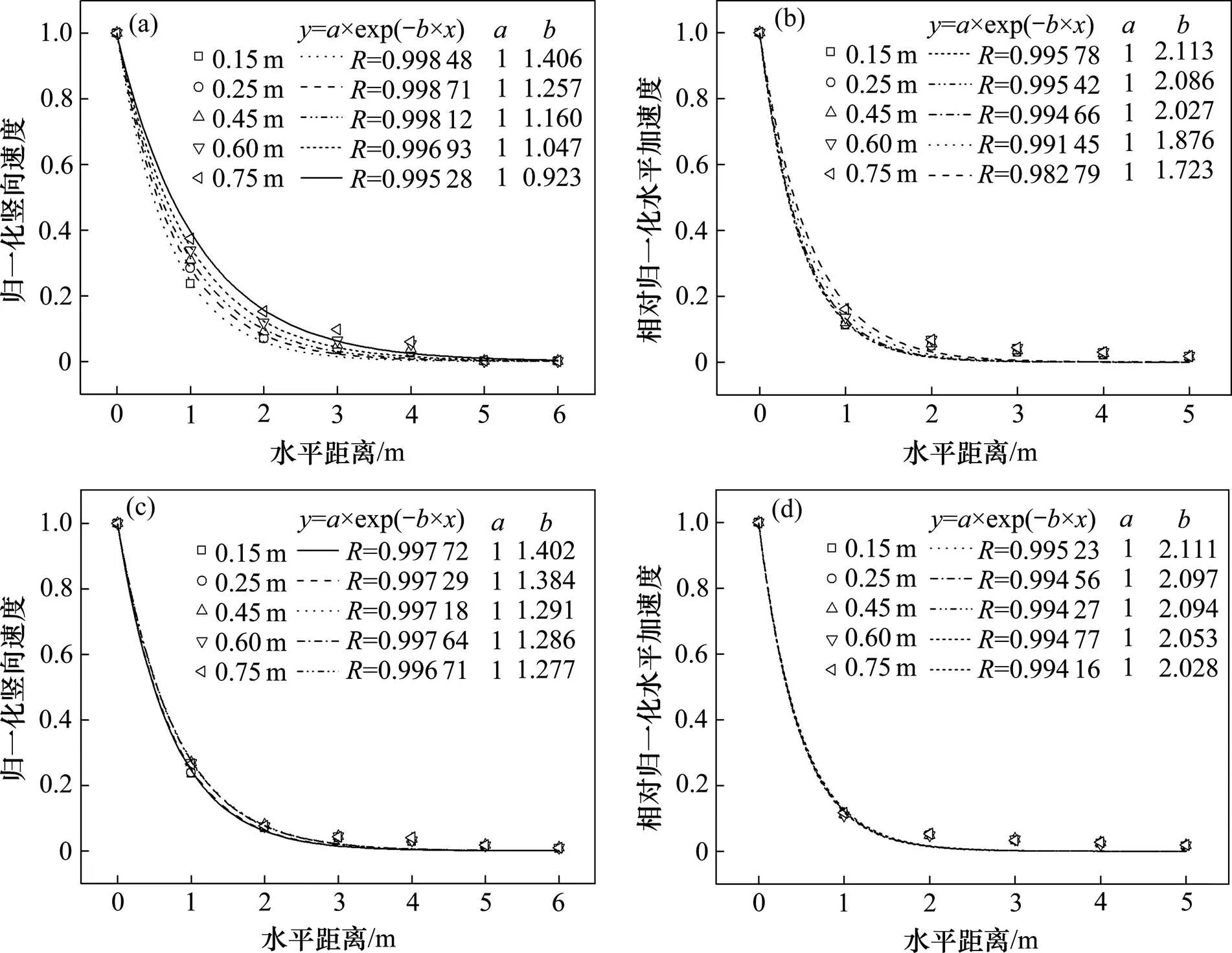
(a) 竖向加速度;(b) 水平加速度;(c) 竖向速度;(d) 水平速度
由图7和图8可知,响应加速度与响应速度的传递和衰减规律相同,响应加速度测试结果无明显波动变化,说明滤波处理可有效减少外界噪声干扰。不同位置处路基的动力响应加速度、速度沿水平方向的衰减规律相近,沿深度方向衰减规律十分接近。响应加速度、速度的竖向分量与水平分量的变化规律基本一致。对比衰减系数可知,响应加速度和响应速度的衰减系数随着深度和水平距离的增加而减小,说明距离激振点越深,沿水平方向衰减越缓慢;距离激振点越远,沿深度方向衰减同样越缓慢。根据振动理论和波动理论分析可知,路基产生的振动以应力波的形式传播,随着水平距离和深度的增加,路基内部应力波的波阵面曲率半径逐渐增加并最终趋近于平面。当路基振动衰减系数减小至0时,将沿路基水平方向和深度方向传播平面波。因此,距离振源越远处的响应加速度和响应速度衰减越缓慢。
为进一步对比分析沿深度方向与沿水平方向的传递和衰减规律、竖向分量与水平分量的传递和衰减规律以及加速度与速度的变化规律,根据图7和图8中的拟合结果,选取衰减系数的最大值和最小值为研究对象,得到如表1所示的沿深度方向和沿水平方向相对归一化后的加速度、速度的衰减系数的对比数据。表中衰减系数越大衰减越迅速,反之衰减越缓慢。

(a) 竖向加速度;(b) 水平加速度;(c) 竖向速度;(d) 水平速度

表1 相对归一化后的衰减系数
由表1可知,沿深度方向的衰减系数约为沿水平方向衰减系数的2.5~3倍,说明响应加速度和响应速度沿深度方向的衰减更显著。沿水平方向衰减时,响应加速度、速度的水平分量衰减系数约为竖向分量衰减系数的1.5~1.9倍,表明水平分量沿水平方向的衰减比竖向分量沿水平方向的衰减更快;沿深度方向衰减时,响应加速度、速度的水平分量衰减系数约为竖向分量衰减系数的0.9~1.0倍,表明水平分量与竖向分量沿深度方向的衰减速度基本一致。对比加速度与速度衰减系数最大值可知,竖向分量衰减系数最大值的比值和水平分量衰减系数最大值的比值均接近于1.0,说明加速度和速度的变化规律相近。另外,对比加速度、速度的衰减系数差值的比值可知,各比值均大于1.0,并且沿水平方向的比值大于沿深度方向的比值,说明加速度的变化幅度更大,加速度对外部激振的响应更为敏感,能够更精确反映衰减规律的细微变化,研究沿水平方向的变化规律时采用加速度指标的优势更明显。
2.3 动态响应范围
为进一步研究路基动力响应的范围,以响应加速度、速度趋近于0时的水平方向5 m和深度方向0.75 m处为研究范围,分别以该范围的加速度、速度之和为归一化基准,得到沿水平方向和沿深度方向的加速度、速度归一化后的累计值,如图9所示。

(a) 水平方向;(b) 深度方向
由图9可知,沿水平方向和沿深度方向的归一化后的累计值的变化规律相似。在靠近振源的某一范围内归一化后的累计值迅速增大,随后逐渐增长缓慢并最终趋近于1。在水平方向1.5 m和深度方向0.45 m范围内累计归一化水平已达到0.9,表明此范围已发生的动力响应占整体动力响应的90%,可认为此范围是路基内部的动力响应区域。
3 结论
1) 基于土体动力互易性原理开展现场激振试验,不仅可以得到可靠的测试结果,而且极大地简化了现场操作。
2) 路基响应速度、加速度沿深度方向和水平方向均呈指数衰减规律,衰减系数随着深度和水平距离的增加而减小,距离激振点越远衰减越缓慢。沿深度方向衰减系数约为沿水平方向衰减系数的2.5~3倍,路基的动力响应沿深度方向衰减更快。
3) 响应加速度、速度的竖向分量幅值约为水平分量幅值的2倍,路基的动力响应主要体现在竖向分量上,但水平分量不容忽视。水平分量沿水平方向的衰减速度约为竖向分量的1.5~1.9倍,水平分量沿深度方向的衰减速度约为竖向分量的0.9~1.0倍,水平分量沿水平方向的衰减相对明显。
4) 进行滤波处理后的响应加速度和响应速度的变化规律相近。加速度对外部激励的响应更为敏感,能够更精确地反映细微变化,建议采用滤波处理后的加速度指标研究路基动力响应规律。
5) 在本实验条件下,水平方向两侧3 m和深度方向0.45 m范围为路基最主要的动力响应区域。
[1] 陈云敏, 边学成. 高速铁路路基动力学研究进展[J]. 土木工程学报, 2018, 51(6): 1−13. CHEN Yunmin, BIAN Xuecheng. The review of high-speed railway track foundation dynamics[J]. China Civil Engineering Journal, 2018, 51(6): 1−13.
[2] Ishikawai T, Sekineiia E, Miura S. Cyclic deformation of granular material subjected to movingwheel loads[J]. Canadian Geotechnical Journal, 2011,48(5): 691−703.
[3] Shaer A A, Duhamel D, Sab K, et al. Experimental settlement and dynamic behavior of a portion of ballasted railway track under high speed trains[J]. Journal of Sound &Vibration,2008, 316(1/2/3/4/5): 211−233.
[4] Indraratna B, Nimbalkar S. Discussion of “stress-strain degradation response of railway ballast stabilized with geosynthetics”[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(5): 684−700.
[5] 牛婷婷, 刘汉龙, 丁选明, 等. 高铁列车荷载作用下桩网复合地基振动特性模型试验[J]. 岩土力学, 2018, 39(3): 872−880. NIU Tingting, LIU Hanlong, DING Xuanming, et al. Piled embankment model test on vibration characteristics under high-speed train loads[J]. Rock and Soil Mechanics, 2018, 39(3): 872−880.
[6] 陈善雄, 宋瑞军, 余飞, 等. 降雨入渗对路基动力响应的变化规律研究[J]. 岩石力学与工程学报, 2017, 36(增2): 4212−4219. CHEN Shanxiong, SONG Ruijun, YU Fei, et al. The change rules of dynamic response on subgrade underThe rainfall infiltration[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(Suppl 2): 4212− 4219.
[7] Thach P N, LIU H L, Kong G Q. Vibration analysis of pile-supported embankments under high-speed train passage[J]. Soil Dynamics and Earthquake Engineering, 2013, 55(12): 92−99.
[8] WANG C, WANG B, GUO P, et al. Experimental analysis on settlement controlling of geogrid-reinforced pile-raft- supported embankments in high-speed railway[J]. Acta Geotechnica, 2015, 10(2): 231− 242.
[9] Yoshitsugu M, Etsuo S, Fumio T. Deformation characteristics of railway roadbed and subgrade under moving-wheel laod[J]. Soil and Foundations, 2005, 45(4): 99−118
[10] 冷伍明, 梅慧浩, 聂如松, 等. 重载铁路路基足尺模型试验研究[J]. 振动与冲击, 2018, 37(4): 1− 6, 18. LENG Wuming, MEI Huihao, NIE Rusong, et al. Full- scale model test of heavy haul railway subgrade[J]. Journal of Vibration and Shock,2018, 37(4): 1−6, 18.
[11] 金书滨, 张长胜, 刘政, 等. 大吨位压路机碾压大粒径填石路基的动力响应[J]. 铁道科学与工程学报, 2016, 13(9): 1743−1748. JIN Shubin, ZHANG Changsheng, LIU Zheng, et al. The dynamic response of large diameter fill subgrade by large tonnage rollers[J]. Journal of Railway Science and Engineering, 2016, 13(9): 1743−1748.
[12] 王子玉, 凌贤长, 惠舒清. 季节冻土区铁路路基振动加速度现场监测[J]. 岩土工程学报, 2015, 37(9): 1591− 1598. WANG Ziyu, LING Xianchang, HUI Shuqing. Field monitorring of vibration response of subgrade in a seasonally frozen region[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(9): 1591−1598.
[13] 屈畅姿, 王永和, 魏丽敏, 等. 武广高速铁路路基振动现场测试与分析[J]. 岩土力学, 2012, 33(5): 1451−1456, 1461. QU Changzi, WANG Yonghe, WEI Limin, et al. In-situ test and analysis of vibration of subgrade for Wuhan -Guangzhou high-speed railway[J]. Rock and Soil Mechanics, 2012, 33(5): 1451−1456, 1461.
[14] Thom N H, Mcdowell G R, Brown S F, et al. The Nottingham railway test facility[J]. UK. Transport, 2007,160(2): 59−65
[15] LIU S, HUANG H, QIU T, et al. Effect of geogrid on railroad ballast particle movement[J]. Transportation Geotechnics, 2016, 9: 110−122.
[16] 付强, 宋金良, 丁选明, 等. 高铁荷载下桩−土复合地基振动响应特性研究[J]. 铁道科学与工程学报, 2017, 14(10): 2050−2058. FU Qiang, SONG Jinliang, DING Xuanming, et al. Study on dynamic response characteristic of PCC pile-soil composite foundation under high-speed railway train load [J]. Journal of Railway Science and Engineering, 2017, 14(10): 2050−2058.
[17] 曹艳梅, 夏禾. 基于Betti-Rayleigh动力互易定理求解移动荷载引起的地基土振动[J]. 岩石力学与工程学报, 2009, 28(7): 1467−1476. CAO Yanmei, XIA He. Solution of foundation soil vibrations induced by moving loads based on Betti- Rayleigh dynamic reciprocal theorem[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(7): 1467− 1476.
Experimental study on spatial characteristics of dynamic responses of high-speed railway subgrade under vibrational loading
WU Longliang1, YU Qi2, JIANG Huihuang1, 3, XIANG Weiguo1, GAO Mingxian3, YAN Xiaoxia3
(1. China Academy of Railway Sciences Corporation Limited, Beijing 100081, China;2. Bureau Public Work of Shenzhen Municipality, Shenzhen 518031, China;3. Shenzhen Research and Design Institute, China Academy of Railway Sciences Corporation Limited, Shenzhen 518054, China)
In order to study the characteristics of dynamic responses of the subgrade under vibrational load, field loading tests were conducted to monitor excitation responses based on vibration velocity and acceleration, and the dynamic response attenuation law of the subgrade along the depth direction and the horizontal direction was obtained. The results show that acceleration and velocity responses are exponentially decayed along the depth direction and horizontal direction, the attenuation along the depth direction is more significant than that along the horizontal direction, and the attenuation coefficient in the depth direction is 2.5~3 times higher than that in the horizontal direction. The further the vibration point is, the slower the attenuation is; the amplitude of the vertical component of the velocity and acceleration responses is about twice of that in the horizontal direction, and the horizontal component of the attenuation velocity along the horizontal direction is about 1.5 to 1.9 times of the vertical component, and the attenuation of the horizontal component of the velocity along the depth direction is about 0.9 to 1.0 times of the vertical component; the acceleration response after filtering is similar to the velocity response. The acceleration response to the external excitation is more sensitive than the velocity, which can better reflect the subtle changes of the attenuation law.
subgrade of high-speed railway; dynamic response; acceleration; velocity; soil dynamic interaction
TU470
A
1672 − 7029(2020)04 − 0799 − 09
10.19713/j.cnki.43−1423/u.T20190610
2019−07−07
中国铁路总公司科技研究开发计划重点课题(2016G006-C);深圳市建筑工务署技术研究课题(THZQ-033-2018)
吴龙梁(1988−),男,湖南岳阳人,博士研究生,从事连续压实控制方面的研究;E−mail:ramlee@126.com
(编辑 阳丽霞)
