基于EIEMD-IMDE-XGBoost 模型的短期电力负荷预测

邢 伟， 母卓元

（内蒙古国合电力有限责任公司，内蒙古自治区 呼和浩特 010060）

0 引言

短期电力负荷预测是电力系统运行及调度的关键，也是系统经济运行的前提条件，能够实现准确的负荷预测，对于电网规划及安全稳定运行具有重要意义。短期电力负荷监测数据具有明显的非平稳特征，如果对其进行预处理，将其分解为多个更为简单的平稳分量，则更容易挖掘出内在特征，有助于实现精确趋势预测。作为一种自适应数据处理方法，经验模态分解方法EMD（empirical mode decomposition） 具有独特的优势，但也存在模态混叠、端点效应等不足[1]。因此，本文在传统EMD 方法基础上提出集成干扰重构经验模态分解方法EIEMD（ensemble interferencereconstructed empirical mode decomposition），可有效缓解模态混叠和端点效应，与此同时，原始数据中不可避免的干扰源也可以彼此相互抵消，从而达到抑制干扰的目的。

信息熵理论可有效反映非线性非平稳数据的特征突变行为，能够准确刻画数据序列的内在状态特征。与传统的近似熵、样本熵、排列熵相比，由Rostaghi 等人[2]提出的散布熵具有实现简便、抗干扰能力强等优点。但其仅能在单一尺度上描述数据特性，而基于粗粒化处理过程提出的多尺度散布熵MDE（multiscale dispersion entropy） 算法[3]则可以描述数据序列在多个尺度上的内在特性，但其算法的熵值计算不稳定。为此，本文提出一种改进多尺度散布熵IMDE（improved multiscale dispersion entropy） 算法，用于刻画电力系统负荷监测数据的内在特征。

由于训练数据少，异常扰动明显，预测实时性要求高，因此对电力负荷预测器的性能提出了更高要求[4]。目前，常用的一些预测器都存在影响参数多、计算负担大、容易陷入局部最优等缺点，为规避此类缺陷，本文将一种新颖的XGBoost模型应用于电力负荷预测[5]，并将其与提出的EIEMD 和IMDE 方法相融合，提出基于EIEMDIMDE-XGBoost 模型的电力负荷预测方法，有望实现准确的预测结果。

1 集成干扰重构经验模态分解

1.1 EIEMD 方法

假设s（t）为真实数据序列，n（t）为干扰源，所监测的原始数据x（t）可表示为x（t）=s（t）+n（t），EIEMD方法的具体实现步骤如下。

步骤1：由于干扰源n（t）=x（t）-s（t），在实际工况中存在各种干扰源nj（t），因此取j∈N。

步骤2：先从监测到的原始数据x（t）中计算干扰源n（t），然后重采样干扰源n（t）获得nj（t）。

步骤3：对原始数据x（t） 进行EMD 处理，EMD 具体原理可参考文献[6]。

步骤4：使用固有模态函数IMF（intrinsic mode function） 分量估计得到干扰分量（t）。

步骤5：再次重采样（t）来得到第j个干扰源（t）。

步骤6：用式（1）再次重构所得数据序列（t）。

其中，（t）=x（t）-（t）。

步骤7：通过EMD 将x^j（t）分解为k个IMF 分量｛cj,（kt），k=1，2，…，n｝和1 个残差分量｛rj,（nt）｝。

步骤8：r次重复步骤5 和步骤7，直到满足敏感评判指标为止。

步骤9：当满足敏感评判指标时，利用式（2）和式（3） 求其均值，最终得到平均处理后的IMF分量和残差分量

1.2 敏感评判指标选取

考虑干扰源影响，引入干扰误差来量化去干扰效果。假定经过r次EMD 处理后获得式（2）、式（3）中的IMF 分量和残差分量，通过式（4）重构去干扰数据（t）。

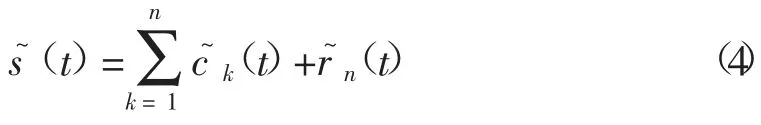
继而得到平均干扰源

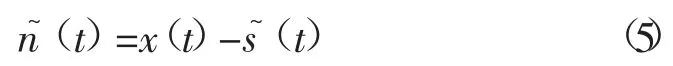
通过式（6）获得相对干扰误差

敏感评判指标依据er＜ε 来选取，其中ε=0.1为预设的误差容限。

2 改进多尺度散布熵

2.1 IMDE 算法

本文对传统多尺度散布熵MDE 算法进行改进，提出IMDE 算法，实现过程如下。

a） 在IMDE 算法中，对于长度为N的原始数据｛x|x1，x2，…，xj，1≤j≤N｝，在尺度条件下的粗粒化序列可通过式（7） 获取。以尺度τ=2、τ=3 为例，MDE 和IMDE 算法粗粒化过程分别如图1 和图2 所示。对比可发现，计算不同尺度下的散布熵时，原始算法仅仅考虑一个粗粒化序列，在改进算法中，对于每个尺度因子τ，可以获得τ 个不同粗粒化序列(k=1，2，…，π)。

b） 对于每个尺度因子τ，计算各粗粒化序列(k=1，2，…，π) 的散布熵值，并根据式（8） 求取散布熵的平均值，则不同尺度因子下对应的散布熵均值即为最终结果，IMDE 表达式为

图1 传统MDE 算法粗粒化示意图

在IMDE 算法中，连续计算了所有粗粒化序列的散布熵值，并通过求均值获取最终的结果，该过程可有效提高所得熵值精确度及计算过程的稳定性，更适合非线性非平稳定时间序列的分析处理。

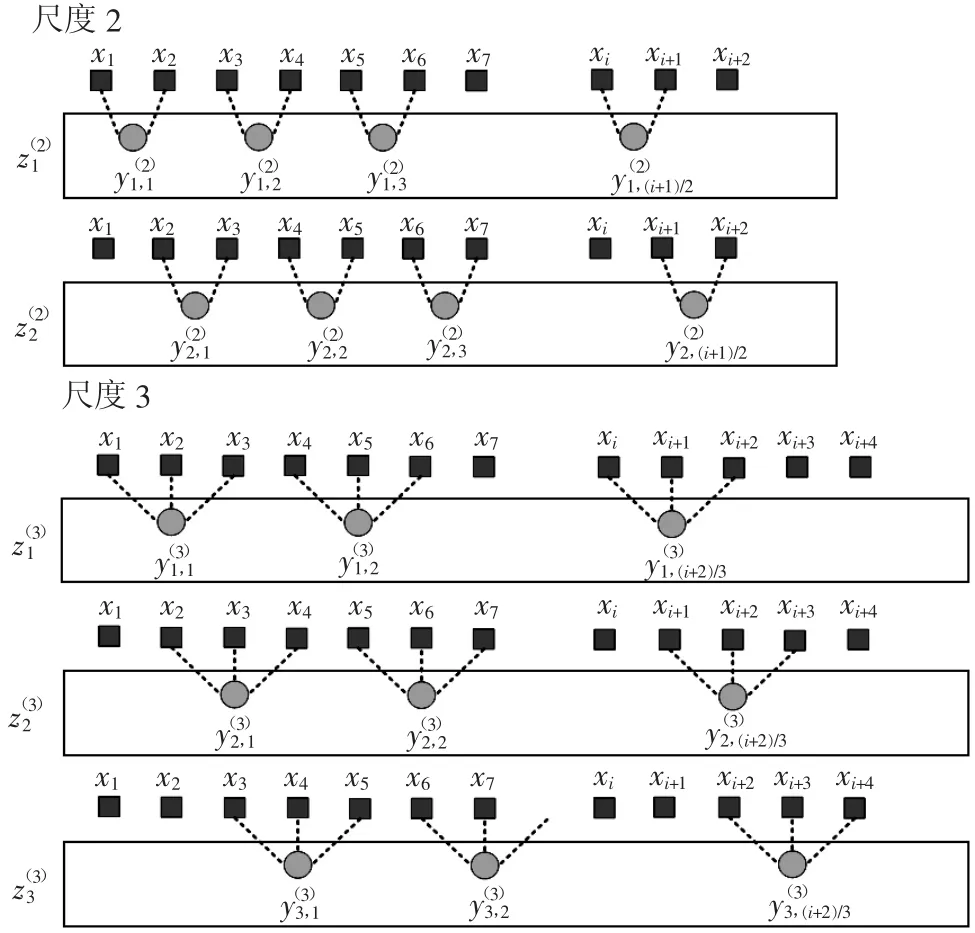
图2 IMDE 算法粗粒化示意图

2.2 计算稳定性对比

构造仿真数据序列来对比传统多尺度散布熵算法及改进多尺度散布熵算法的计算稳定性。给定一个功率谱与频率满足S（f）∝1/fα条件的自相似随机时间序列，当α=0 时属于高斯序列，当α=1 时属于分数阶序列[7]。

分别计算这两种数据序列的熵值曲线，对比可发现，由于分数阶序列比高斯序列更加复杂，具有长程相关性，其散布熵值较大，而高斯序列则不具有这一性质，因此其散布熵值更小。随机生成30 个分数阶序列，每个序列1 000 个数据点，计算IMDE 及MDE 误差曲线，由此给出不同尺度下两种算法所得熵值的均值及标准差，用于验证二者的稳定性，结果如图3 所示。观察可发现，IMDE 所得熵值的均值与MDE 相比，变化更平缓，稳定性更好，并且熵值的标准差明显更小，高斯序列对比结果与此相同。由此表明所提出的IMDE算法计算过程更加稳定、准确，在描述数据序列内在特性方面更胜一筹。

3 XGBoost 模型

XGBoost 基于损失函数2 阶泰勒展开进行优化，提升了可分性，为避免过拟合和降低模型复杂度，在损失函数之外还引入了正则项整体求最优解[8]。

图3 分数阶序列误差曲线

假设模型有k个决策树，即

其损失函数为

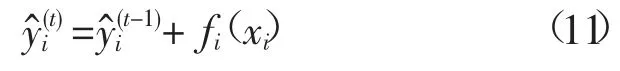
损失函数可表示为

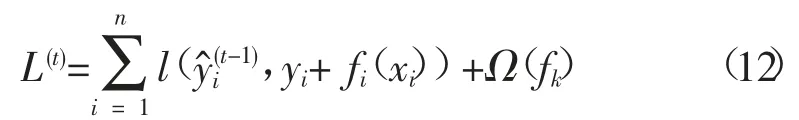
对损失函数泰勒展开有

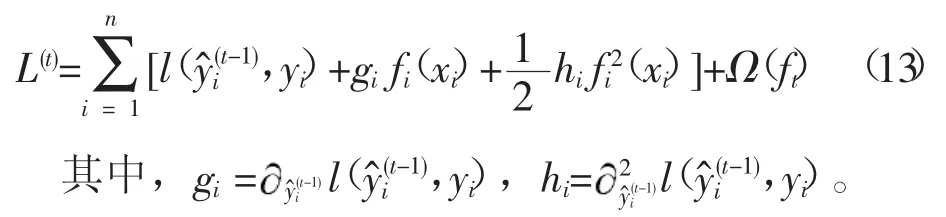
移除常数项得到

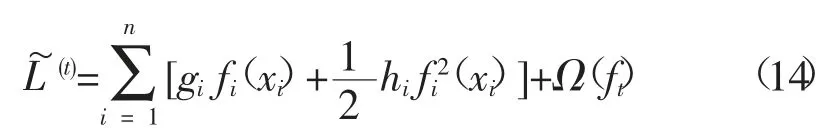
定义Ij=｛i|q(xi=j｝) 为第j个叶子点，即

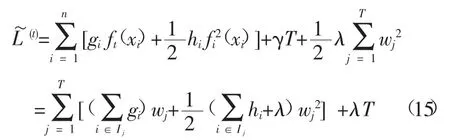
将式（15） 求导并令结果为0，则可得

把wj最优解wj*带入目标函数，可得最终结果

XGBoost 的分割步骤发生在每个已有的叶子节点，取代了传统分割标准最小化均方差的方法，能够更加有效地枚举树的结构。

4 短期电力负荷预测流程

电力系统负荷监测数据是一种具有周期性、随机变化性与趋势性的复杂非平稳数据。为了提高电力负荷预测的精度，本文提出了基于EIEMD-IMDE-XGBoost 模型的方法，预测流程如图4 所示，具体实现步骤如下。

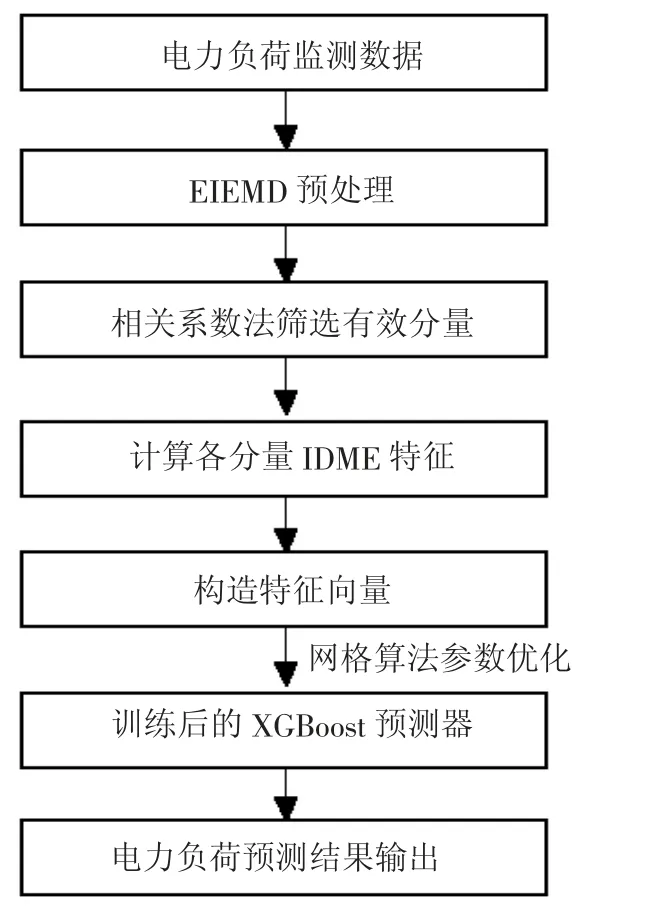
图4 电力负荷预测流程

步骤一：对原始电力负荷数据进行预处理，利用EIEMD 方法将其分解为若干平稳的IMF 分量。步骤二：通过计算所得各IMF 分量与原始数据序列的相关系数，将相关系数大于0.1 的IMF分量作为有效分量予以保留，同时剔除无效分量。步骤三：计算所得有效IMF 分量的IMDE 特征，合并后由此构造特征向量。IMDE 计算过程选取嵌入维数m时，如果m取值过小则难以有效检测序列特性，反之则无法区分其波动状态，综合比较后取m=3。设置类别个数c过小，则差异较大的数据点容易被划分为同一类别，取值过大则计算效率降低，本文取c=5 来保证结果的可靠性。由于时延参数对计算过程影响很小，本文直接取λ=1。至于尺度的选取，设置过小难以完整提取有效信息，较大则容易导致计算不稳定，综合考虑后取τ=20。步骤四：利用所构造的训练样本特征向量对XGBoost 模型进行训练，在训练过程中，以对数损失为准则，通过网格搜索预测器的最优决策树规模及深度参数。步骤五：构造测试样本的特征向量，并输入到训练好的最优XGBoost 预测器中，输出最终预测结果。

5 实例分析

以内蒙古呼和浩特市2018 年全年用电量为例，以1 h 为间隔全程监测该市2018 年1 月1 日至12 月31 日的电力负荷数据。本文将2018 年8月1 日至10 月30 日的监测数据作为训练样本。

首先利用EIEMD 算法对原始数据进行预处理，共得到如图5 所示的8 个IMF 分量和1 个余量。继而计算所得分量与原始数据的相关系数，用于有效分量的选取，结果如表1 所示。由于前4 个分量的相关系数大于设定的阈值0.1，因此将IMF1～IMF4 作为有效分量予以保留，同时计算各有效分量的IMDE 值，由于每个分量得到20 个散布熵值特征，因此最终构造出由80 个散布熵值组成的特征向量，同时将其输入到XGBoost 预测器中对其进行训练。

图5 原始负荷数据EIEMD 处理结果

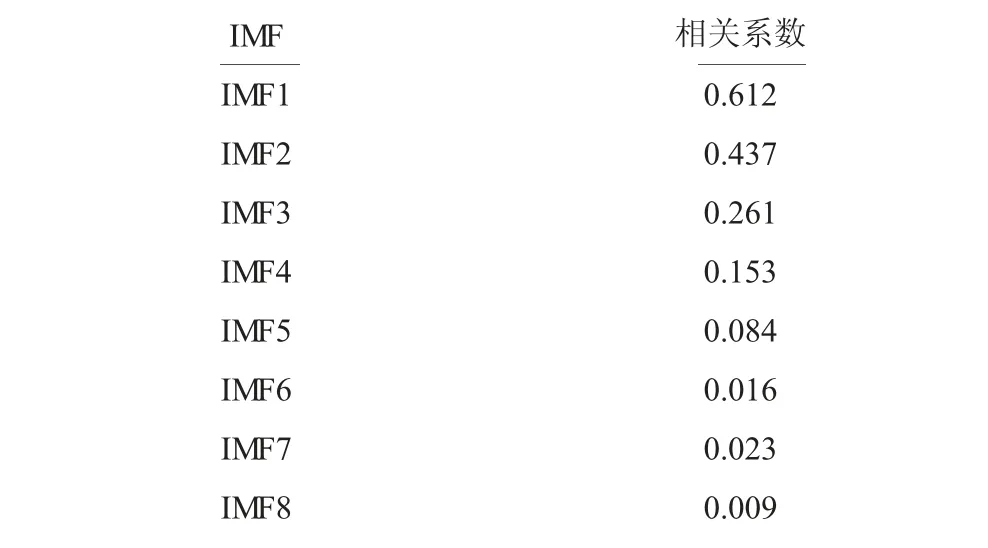
表1 各分量与原始数据的相关系数

XGBoost 在顺序创建或者增加决策树时，每个决策树都会试图去纠正之前预测中存在的错误，当树的规模达到一定程度后，预测效果已达到最优，即使再增加树的棵数及深度，效果也不会出现明显提升，反而会影响预测效率。因此，本文利用网格搜索方法对决策树的规模及深度进行寻优。在寻优过程中，利用对数损失作为指导标准，对数损失越小达到的效果就越好。由于XGBoost模型中默认树的棵数为100，本文在寻优时围绕这一参考量将树的规模取[50，100，150，200]，深度取[2，4，6，8]，参数寻优结果如图6 所示。由图6 可知，决策树的深度取4、规模取150 时，预测效果已经达到最优，因此在该参数条件下进行测试分析。

图6 决策树的规模与深度寻优曲线

将呼和浩特市2018 年10 月31 日当日监测数据作为测试样本来验证所述方法的可靠性，图7为预测结果与当日实际负荷的对比。为定量衡量预测结果的可靠性及准确性，引入相对误差RE指标进行评判[9]。

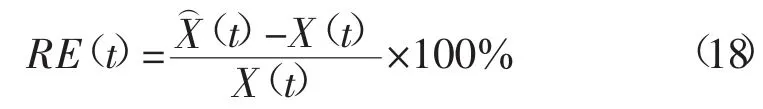
其中，X（t）为电力负荷实际监测值，（t）为通过预测方法得到的预测负荷值。

通过观察图7 可发现，本文所述方法的预测结果走势与实际负荷值基本保持一致，仅在前6个时间点处存在一定偏差，但最大相对误差值也仅为-2.7%，后续18 个时间点预测结果更加精确，与实际负荷值相对误差均保持在1%以内，偏差值波动很小。总体来看，本文所述方法的预测结果较为准确，对于电力系统调度应用可提供较高的参考价值。

图7 本文所述方法负荷预测结果

为了突出所述方法的优势，将所得结果与其他4 种不同预测方法结果进行对比。在方法1（EIEMD+MDE+XGBoost） 中，利用传统MDE 算法来提取有效分量的内在特征并构造特向量；在方法2（IMDE+XGBoost） 中，原始负荷监测数据不经过EIEMD 预处理，直接计算其IMDE 特征，并构造维度为20 的特征向量；在方法3（EIEMD+MDE+SVM） 中，数据预处理及特征向量构造过程不变，利用广泛应用的SVM 预测器来替换XGBoost 预测器；在方法4（EIEMD+MDE+BP）中，利用BP 神经网络预测器来替换XGBoost 预测器。经过计算各方法的预测相对误差曲线，结果显示本文所述方法在各个时间点处预测相对误差变化较为平滑，误差值最小，而其他4 种方法得到的相对误差波动幅度均较大。由此验证了本文所述方法在电力负荷监测数据内在特征描述以及预测性能上的优势。

6 结束语

电力负荷短期预测是电力系统调度运营部门的日常工作，已成为电力企业现代化管理的重要内涵之一。本文将XGBoost 模型引入电力负荷预测领域，提出了基于EIEMD-IMDE-XGBoost 模型的新方法，填补了现存预测方法存在的不足。实例验证结果表明，该方法能够高效、可靠、准确地实现电力负荷短期预测，可为发电计划和输电方案的制定提供参考，对于实际工程应用具有一定借鉴价值。