基于SIMULINK 的振动传递路径系统灵敏度分析

秦净净，王 宇

（黄河水利职业技术学院，河南 开封 475004）

0 引言

振动系统包括振动源、 振动传递路径和振动接受结构3 部分［1-3］。研究表明，控制振动的噪声源、切断传递路径、保护接受体是减振降噪的3 种措施。因此，研究振动传递系统预测模型和动态设计，可以为解决工程中的振动和噪声问题提供有效的途径，但是清晰地阐述多维路径的贡献量并不是一件容易的事情［4-5］。目前，关于振动源、传递路径和接受结构的交互作用的研究还处于初级阶段， 主要集中于实验方法和能量传递方法上［6-8］。张义民等基于随机摄动法和振动系统传递路径灵敏度分析， 提出了一种时域内计算系统参数灵敏度和传递路径灵敏度的有效方法， 定义了相应的系统参数和传递路径灵敏度指标［9］。 赵薇等建立了具有路径质量的振动传递路径系统模型， 将矩阵微分理论与振动力学理论结合起来， 对频域内振动传递路径系统的参数灵敏度进行了论述， 探讨了接受体频域动力学响应对路径参数灵敏度的影响［10］。但是，受制造环境、技术水平、安装条件等因素的影响，工程结构系统的材料特性、几何尺寸和边界条件等参数变化具有随机性［11］。鉴于此，笔者基于一般概率摄动有限元法和结构系统响应的随机性理论， 试运用MATLAB 的一个附加组件SIMULINK，把传递率作为度量指标，描述振动传递路径系统的路径传递率的排列顺序， 并对其进行灵敏度分析， 以期为识别各传递路径参数的贡献度提供理论支持。

1 振动系统传递路径分析的理论基础

1.1 路径模型

在分析振动对噪声的影响时， 常常需要分析激励（输入）和响应（输出）之间的关系。为简单起见，本文选取图1 所示的单激励有阻尼的两自由度的传递路径系统模型进行分析。

根据牛顿定律，模型的表达式如式（1）所示。

图1 振动传递系统路径系统模型Fig.1 Vibration transmission system path system model

设稳态响 应为Xs（w）＝Xsei（wt-φ），Xr（w）＝Xrei（wt-φ）。这里Xs和Xr是决定激励频率ω 和系统参数的实数。 将Xs和Xr代入式 （1）， 得到相应的特征行列式，如式（2）所示。

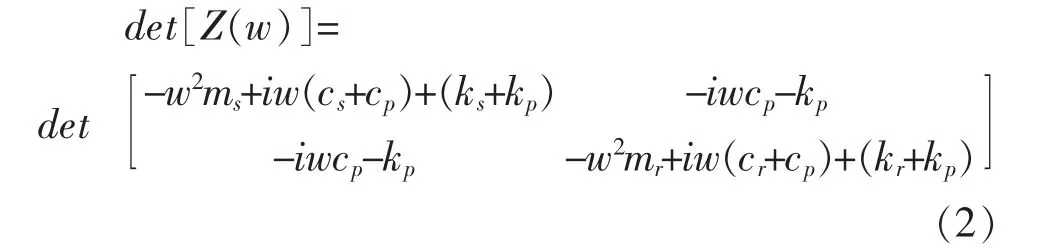
经过一系列推导， 将传递率定义为实际传递力的力幅与激励力幅之比，如式（3）所示。

1.2 路径传递度

考虑到系统参数的随机性，设随机参数向量b＝（kp1kp2kp3cp1cp2cp3）T代表路径的随机性， 则传递力FTpj（j＝1，2，3）为随机变量，X（b，w）为外激励频率w和设计参数b 的函数。

由于X（w）＝Xei（wt-φ），则方程（2）可表示为式（5）。

式（3）两边同时对b 求导，得式（6）。

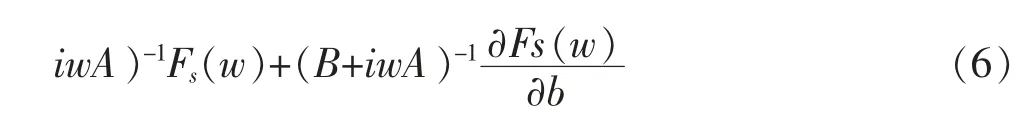
2 数值算例

某振动传递路径系统的模型如图1 所示， 其振源系统的质量ms＝8 kg、 阻尼系数cs＝0.5 N·s／m、刚度ks＝10 N／m，接受系统的质量mr＝8 kg、阻尼系数cs＝1.0 N·s／m、刚度kr＝180 N／m，激励幅值（确定性变量）F0＝100 N、频率w＝100 rad／s。 随机路径以随机参数向量b＝（kp1kp2kp3cp1cp2cp3）T为代表， 路径的随机阻尼系数和弹性刚度分别服从方差为0.05 的正态分布，3 个路径的阻尼系数和弹性刚度的均值分别为：cp1＝0.5 N·s／m，cp2＝0.75 N·s／m，cp3＝0.25 N·s／m，kp1＝450 N／m，kp2＝225 N／m，kp3＝300 N／m， 分析此振动传递系统的各路径的传递率和参数敏感性。

2.1 数值模型的建立

对于振动问题的求解，传统计算模式多借助于数值方法， 但这种方法需要编制复杂的计算程序。SIMULINK 是MATLAB 的一个附加组件， 也是一种用来实现计算机仿真的软件工具， 可用于实现各种动态系统（包括连续系统、离散系统和混合系统）的建模、分析和仿真。

运用SIMULINK 建立如图2 所示模型， 则得到该系统两个振型的时程曲线，如图3 所示。该系统的固有频率为w1＝3.939 7 rad／s，w2＝15.308 3 rad／s。

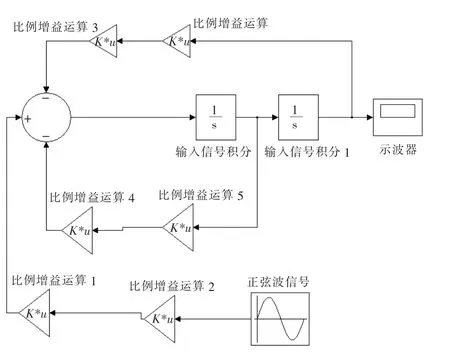
图2 SIMULINK 模型示意图Fig.2 Schematic diagram of SIMULINK model

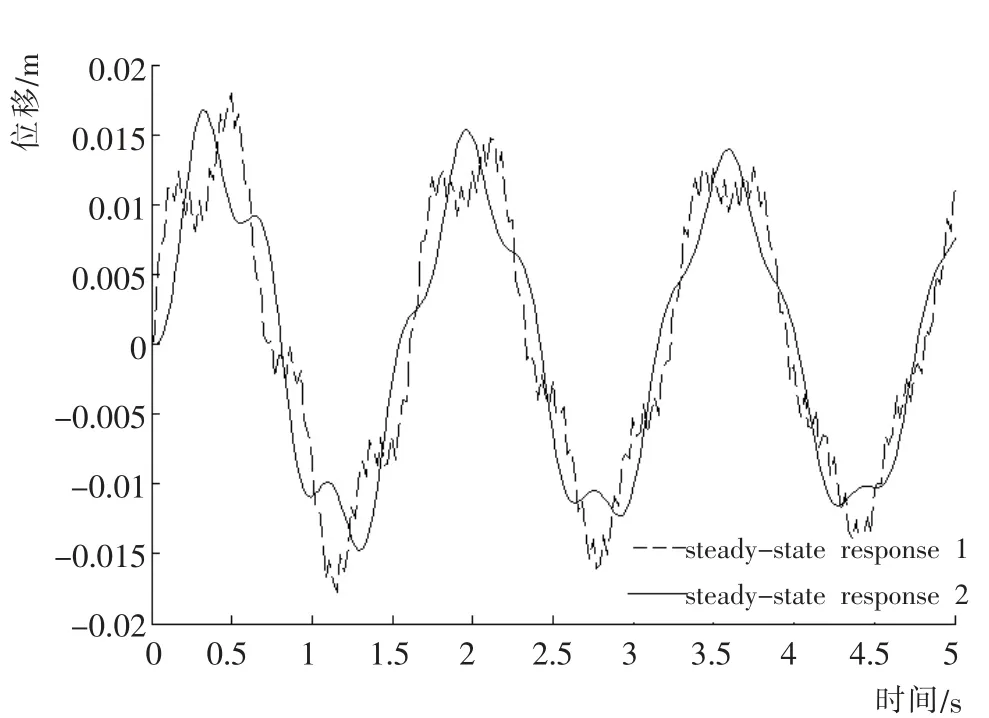
图3 稳定位移响应时程曲线Fig.3 Stable displacement response time history curve

2.2 路径传递灵敏度分析

分别计算3 种路径状况下各路径的传递率，并绘出路径传递率与激励频率ω 的关系曲线， 如图4所示。

图4 路径传递率关于激励频率的特性曲线Fig.4 Characteristic curve of path transfer rate with respect to excitation frequency

从图4 中可以看出，在两个固有频率（w1和w2）处，3 种路径的传递率都很高。 其中，路径1 对接受结构振动的贡献度最大，其次是路径2，最后是路径3。 因此，在实际中，应更多地关注路径1 的参数变化，以便为抑制振动和控制噪声提供度量依据。

2.3 振动系统路径阻尼和刚度对位移响应参数的敏感度分析

为了研究系统振动中路径阻尼和刚度对位移响应的参数敏感度，以便有效进行低振动与噪声设计，以及通过采取相应技术措施把系统的振动噪声降低到符合国家标准的范围内。 分别计算在3 种路径情况下，在频域响应过程中，位移响应对路径刚度和路径阻尼的影响程度，结果如图5 和图6 所示。

从图5 和图6 可知， 路径刚度和路径阻尼对接受体位移的震荡趋势与系统路径传递率在频域内的振荡趋势相同， 路径阻尼对接受体频域响应的影响程度大于路径刚度的影响程度。 因而路径阻尼的灵敏度大于路径刚度的灵敏度， 成为系统重要的路径参数。

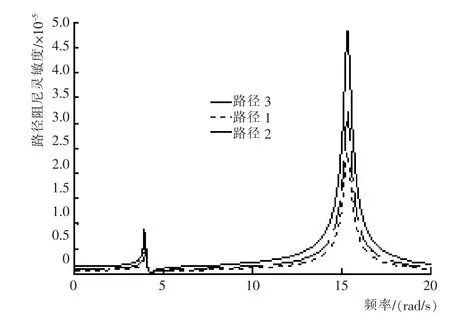
图5 位移响应对路径刚度的灵敏度Fig.5 Sensitivity of displacement response to path stiffness

图6 位移响应对路径阻尼的灵敏度Fig.6 Sensitivity of displacement response to path damping

3 结语

综上所述， 本文采用基于一般概率摄动有限元法和结构系统响应的随机性分析方法， 对频域内振动传递路径系统的路径传递率进行了探索， 以确定各路径对接受结构振动的贡献量， 并对振动传导路径系统进行了灵敏度分析， 得出以下结论：（1）SIMULINK 计算方法简单、快捷，其过程是建立数学及仿真模型，并不需要编辑大量的复杂程序，且所得结论可靠。（2）路径刚度和路径阻尼对接受体位移的震荡趋势与系统路径传递率在频域内的振荡趋势相同， 路径阻尼对接受体频域响应的影响程度大于路径刚度的影响程度。因而，路径阻尼的灵敏度大于路径刚度，是系统路径的重要路径参数。