基于过渡工作过程的航空发动机气路分析方法

杨锟，张鑫，屠秋野，陈飞阳，郑康

(1.西北工业大学 动力与能源学院，西安 710129) (2.中国航发湖南动力机械研究所 发动机总体研究部，株洲 412002)

0 引 言

航空发动机健康监测的目标是掌握发动机各部件的性能退化程度，即获得相应部件在特定工作状态下健康参数的量值，它们通常与旋转部件的流通能力、做功效率，燃烧室反应效率、燃油泵延迟，高/低压轴承的摩擦损失，气路的漏气比例以及变几何机构的控制参数等的变化相关。上述健康参数通常无法通过传感器直接测量，因此需要采用气路分析(Gas Path Analysis)技术并利用发动机气路传感器测得的各旋转部件转速以及部分截面的压力和温度等对相应的健康参数进行估计。

自从L.A.Urban[1]将基于线性模型的气路分析方法引入航空发动机状态分析以来，绝大多数的气路分析研究均基于发动机的稳态过程[2-7]。然而从工程实践的角度来说，稳态数据经常难以获得[8]，且在实际某个航段获得多个稳态工作点的数据更不现实。在民航客机特别是国内航线上运行的发动机，存在着相当比例的过渡工作状态，而这一状态在军用发动机的工作过程中占比甚至达到了70%[9]。此外，由于发动机的很多故障特征仅在过渡工作状态下才能表现出来，使用相对更容易获得的过渡态数据能够更全面的对发动机的健康状态进行评估。

目前过渡态气路分析中比较有代表性的工作有：T.Groenstedt[10]发展了基于最小二乘的扩展常微分代数方程算法；Li Yiguang[11]提出了以积累误差构建目标函数的理论；J.C.Simmons等[12]和J.R.Mc Cusker等[13]分别对过渡态输出信号进行了小波分析，前者获得了故障特征并以此为基础开发出一套适合机载系统使用的快速诊断方法，后者实现了对测量参数的选择并对性能参数进行了非线性最小二乘估计。但是上述研究均未对影响发动机动态性能的关键参数进行分析，也无法解决在测量传感器数目少于待求健康参数数目情况下的大偏差发动机气路分析问题。

本文首次提出基于过渡工作过程的航空发动机大偏差欠定气路分析方法，是为在测量传感器数量有限的条件下，实现对包含表征发动机机动性能在内的大量关键气路部件健康参数精确估计的系统方法。该方法基于发动机非线性模型，采用序列工作点分析方法，并应用间接递归牛顿-拉夫逊法强化非支配分类差分进化算法(Indirectly Recursive Newton-Raphson Method Enhanced Non-dominated Sorting Differential Evolution Algorithm)执行健康参数估计的数值计算。其优点是能够区分在同一过渡工作过程中不同功率条件下退化程度的差异，且在提升发动机大偏差性能退化条件下全局寻优能力的同时，平衡演化算法的高计算时间成本。通过对多组序列工作点算例的应用以及对算法性能的分析，验证本文方法的有效性。

1 模型理论

采用基于非线性模型的方法对发动机的健康状态进行估计，研究对象为某型大涵道比分开排气涡轮风扇发动机，其布局如图1所示。

图1 分排涡扇发动机示意图Fig.1 Schematic diagram of separated flow turbofan engine

发动机模型的数学描述为一组非线性方程组：

(1)

z(t)=g[(x(t),u(t)]

(2)

式中：x为发动机性能参数向量；u为发动机输入向量(包括飞行高度、马赫数和燃油流量等)；z为发动机测量参数向量。式(1)左边部分分量为零。

将上述非线性模型进行扩展，嵌入部件健康参数向量θ，构建发动机非线性状态分析模型：

(3)

z(t)=g[(x(t),u(t),θ(t)]

(4)

式中：θ各分量由对应部件性能参数的相对值定义，其形式为

(5)

式中：X为特定的部件性能参数；下标d、c分别表示实际退化发动机与标准发动机；p为健康参数向量维度。

状态分析模型中健康参数偏差的定义为

Δθi,d(t)=θi,d(t)-1 (i=1,…,p)

(6)

在对健康参数进行估计的过程中，需对非线性模型进行线性逼近并实施迭代计算，其过程如下：

(7)

(8)

(9)

式中：q为测量传感器数目。

将式(7)写为差值形式：

(10)

(11)

(12)

根据式(10)可以给出健康参数估计的最小二乘迭代格式：

(13)

式中：k为迭代步数。

利用式(13)进行迭代计算的原理如图2所示。

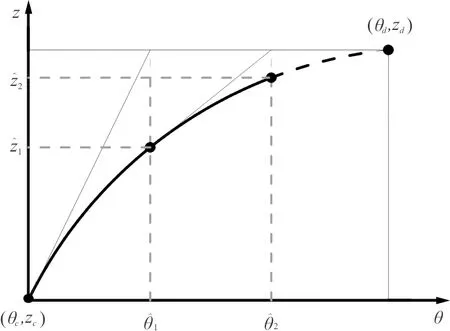
图2 迭代计算原理示意图Fig.2 Schematic diagram of iterative computation

2 大偏差欠定气路分析方法

2.1 序列工作点分析技术

考虑式(13)的构造形式，Jacobi矩阵J的行数应该大于或等于列数，而在测量传感器数目较少的情况下，这一条件并不满足。因此，本文采用基于多工作点分析(Multiple Operating Points Analysis，简称MOPA)[14]思想的序列工作点分析技术(Sequential Operating Points Analysis，简称SOPA)[15]对Jacobi矩阵进行扩维。SOPA方法在发动机的某段过渡工作过程中选取特定传感器布局下一组采样频率为10 Hz(气路传感器信号的带宽为5～20 Hz[16])的连续测量数据进行气路分析。序列工作点选取在发动机某加速过程工作线上的分布如图3所示。

图3 序列工作点选取示意图Fig.3 Schematic diagram of sequential operating points

在不考虑传感器故障的前提下，序列工作点的数量l需满足如下条件：

p≤l×q

(14)

(15)

(16)

式中：T为t时刻(如图3所示)对应的采样点。

基于序列工作点的迭代更新格式为

(17)

2.2 间接递归牛顿-拉夫逊法强化非支配分类差分进化算法

本文提出间接递归牛顿-拉夫逊法强化非支配分类差分进化算法，其流程如图4所示，通过结合进化算法的全局搜索能力与确定性算法的局部逼近能力，为大偏差气路分析问题提供一种解决思路。

在不考虑测量噪声的情况下，在各序列工作点构造子目标函数：

(18)

多目标进化算法能够将散布在整个搜索空间的非支配个体逐步向局部最优解或全局最优解聚集，但是由于演化过程的随机性，准确判断非支配个体进入全局最优解凸邻域范围的时机并不现实，故本文算法采用一种特殊的后验偏好衔接(A Posteriori Preference Articulation)[17]方式：渐进后验偏好衔接(Progressively A Posteriori Preference Articulation)，即在种群的进化过程中，按照一定的代数间隔选择非支配个体执行最优解决策，如果达到决策目标，则算法结束，否则继续演化进程。其中，非支配个体的演化过程采用非支配分类差分进化算法(Non-dominated Sorting Differential Evolution，简称NSDE)，通过将NSGA-Ⅱ[18]中的遗传算法(GA)替换为基本差分进化算法(DE/rand/1)构建。

图4 间接递归牛顿-拉夫逊法强化非支配 分类差分进化算法流程Fig.4 Indirectly recursive Newton-Raphson method enhanced nondominated sorting differential evolution flowchart

最优解决策的过程采用间接递归牛顿—拉夫逊方法(Indirectly Recursive Newton-Raphson Method，简称IRNRM)，其构建思路如下：

3 算例分析

以某型大涵道比双轴分排涡扇发动机作为研究对象进行方法验证，其布局如图1所示。给定发动机工作高度和马赫数，燃油计划如图5所示。

图5 目标发动机燃油计划Fig.5 Fuel schedule of target engine

待分析部件性能参数为风扇、增压级、压气机、高压涡轮、低压涡轮的换算流量Γ和效率η，高压轴承、低压轴承的摩擦损失μ，压气机导叶调节角度β，燃烧室燃烧效率η以及燃油泵延迟τ，即p=15，如表1所示(第一列)。将测量传感器布置给定为(如图1所示)：增压级出口总压p25、压气机出口总温T3、压气机出口总压p3，即q=3。在持续时间为5 s的加速工作过程中，于t分别为1.0、1.5和3.0 s处各选取一组序列工作点(如图6所示)的测量数据分别采用如图4所示算法进行气路状态分析。其中每组序列工作点包含5个连续的发动机状态点以满足式(14)条件，即l=5。

(a) 算例1

(b) 算例2

(c) 算例3图6 在过渡工作过程中包含t=1.0 s,t=1.5 s 以及t=3.0 s时刻的序列工作点选取示意图Fig.6 Schematic diagram of sequential operating points including t=1.0 s,t=1.5 s, and t=3.0 s

本文以预先植入性能偏差的发动机非线性模型仿真数据代替真实发动机的测量数据，待估计性能参数偏差的植入值、搜索范围，以及在各算例中使IRNRM决策计算过程收敛的非支配个体取值、健康参数估计结果和计算所需机时如表1所示。假设传感器测量准确且不受噪声影响，表中所列部件的健康参数偏差同时存在。另需说明的是，虽然本文在整个过渡工作过程中均采用了表1所列的植入健康参数偏差，但这并不代表在实际发动机工作过程中健康参数的偏差值是恒定的。

表1 发动机性能参数植入偏差、搜索范围以及估计结果

从表1可以看出：采用本文所提出的方法，仅利用有限的测量传感器布置即能实现大偏差范围内多于测量传感器数目的大量健康参数的精确估计，而较低的计算时间成本也体现了本文优化方法的计算效率。另需说明的是，本文所采用的传感器布置(p25、T3、p3)在该过渡工作过程不同位置的序列工作点上应用时，其参数辨识能力存在一定差异，从而会影响算法的收敛性及计算效率，但是由于该部分内容不属于本文的讨论范围，在此不再赘述。

以图6中算例1为例，进一步论证本文的参数估计方法：NSDE的种群大小设置为NP=100，差分变异操作中缩放因子F=0.5，交叉概率Cr=0.5。算例1在非支配解搜索过程中起始代(第0代)、中间代(第10代)以及终了代(第20代)非支配个体的分布情况如图7所示。由于可视化呈现的维度限制，图中仅选择健康参数中压气机流量偏差、效率偏差两个分量进行展示，纵坐标OF取值为式(18)中各子目标函数平方和的正二次方根。

(a) 起始代

(b) 中间代

(c) 终了代图7 典型代数非支配解相对真实解的分布Fig.7 Distribution of nondominated solutions for representative generations relative to the true solution

从图7可以看出：伴随演化过程的进行，非支配解的数量逐渐增多，且在空间中向真实解聚集；根据图4所列流程，图7中所列非支配解均需经历决策过程；当某代种群非支配解集中某个体足够接近真实解(即进入了真实解的凸邻域范围内)时，以其作为初值的IRNRM决策过程计算收敛并可最终获得真实解；而图7(c)所示终了代编号为13的非支配个体(个体取值如表1阴影列所示)即满足了上述条件，以其作为初值进行IRNRM最优决策计算收敛。

由决策计算中各步迭代结果的均方根误差(RMSE)所表示的收敛历史如图8所示。

图8 算例1终了代13#非支配个体IRNRM 决策过程收敛历史Fig.8 Convergence history of No.13 nondominated individual in the 20th Generation of Case 1

4 结 论

(1) 本文提出的基于过渡工作过程的气路分析方法，可以实现对压气机变导叶角度、燃油泵控制延迟等发动机关键机动性能参数的退化估计。

(2) SOPA方法既能解决工程实际中待求健康参数较多而测量参数不足所导致的欠定问题，又可以在最大程度上降低由多工作点分析方法的平均效应所引入的参数估计系统误差。具体到本文结果，该方法能够在仅利用3个低温截面传感器测量信息的条件下，确定发动机在不同功率条件下(针对不同算例)由15个健康参数描述的真实健康状态。

(3) 本文提出的间接递归牛顿-拉夫逊法强化非支配分类差分进化算法，既具备全局搜索能力，又能够实现高效高精度的局部逼近。该算法能在配置一般的个人电脑上于数小时内完成大偏差参数空间内健康参数的精确求解。

综上所述，本文所提出的系统性方法能够有效地解决涵盖发动机机动性能退化的大偏差欠定气路分析问题。