基于欧雷准则的某纯电动车悬架刚度优化匹配研究

田玲玲 郝文权 蒋永峰

（中国第一汽车股份有限公司 研发总院，汽车振动噪声与安全控制综合技术国家重点实验室，长春130013）

主题词：欧雷准则 精准 舒适 优化匹配 电动汽车

1 概述

悬架是汽车的重要总成之一，悬架的运动特性直接决定了整车的性能，影响汽车行驶平顺性、操纵稳定性和制动性能。目前，国内多数主机厂悬架的自主开发多是借鉴竞品车型进行逆向设计，悬架性能主要是靠后期实车调校、改善整车性能，开发周期长，成本高。对于前后悬架固有频率的匹配问题，国外学者做了很多研究且应用较成熟，如Hormoz等指出用Olley准则指导悬架平顺性设计[1]。但这些方法在国内主机厂自主开发悬架应用中存在不足，需要做适应性改进。国内学者做了一些研究，如文献[2]、[3]基于整车性能，对悬架进行了优化匹配，但这些方法仅限于仿真对比，没有实际工程应用。本文从与平顺性强相关的前后悬架偏频入手，对欧雷准则进行了理论分析，以车辆二自由度模型为基础研究了前、后悬架刚度优化匹配的方法，并在某电动车动力学性能开发前期得以应用，通过实车试验与优化结果比较，充分验证了该方法具有一定的工程应用价值，并且大大缩短了样车调校时间。

2 欧雷准则及其应用理论推导

2.1 欧雷准则内容

在平顺性研究中，现代汽车动力学创始人之一欧雷(Olley)在研究著名的“k2”车的实验中发现有良好平顺性的车辆需要满足以下准则，后人称之为欧雷准则[1,4]：

（1）前悬架的刚度应比后悬架低30%。

（2）俯仰与跳动频率不应相隔太近，俯仰至少是跳动频率的1.2倍以上，主要是由于频率靠近2种运动的重叠可能产生干扰冲击。

（3）前、后偏频不应超过1.3Hz，车辆的有效静挠度必须超过152.4 mm。

因为欧雷准则是一个从实验中总结出来的准则，没有形成具体的理论，无法对前后悬架刚度进行精准匹配。本文对欧雷准则进行理论分析，研究车辆平顺性，为实现平顺性性能正向开发提供理论依据。

2.2 2自由度车辆模型的解耦

由于主要研究车辆俯仰和弹跳2个方面的表现，故将车辆简化为如图1的2自由度模型系统[5-6]。在两根弹簧上，放置一个长度为L、质量为m、绕质心C的俯仰惯量为I的梁，以此来模拟车辆的跳动和俯仰。

对于如图的带有减振器的系统，很容易得到下面的关系：

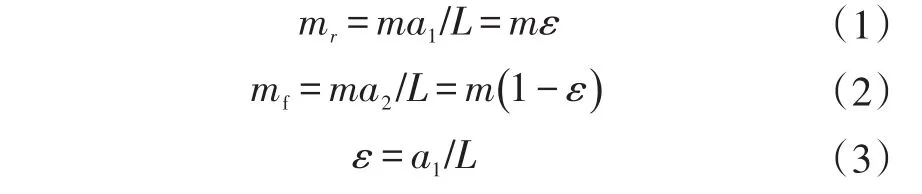
相互独立的系统的方程分别为：

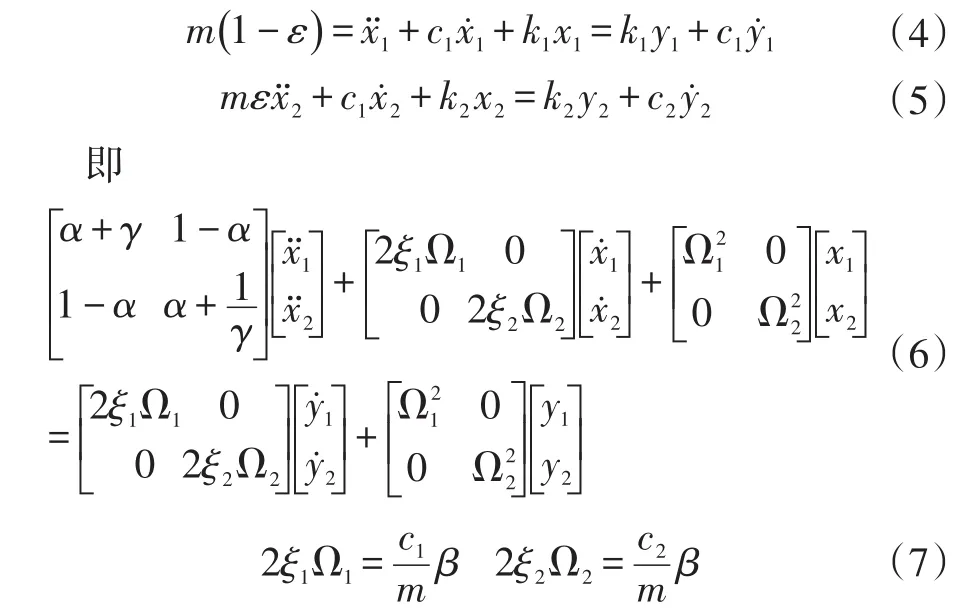
很显然，在α=1时跳动和俯仰被解耦。式中

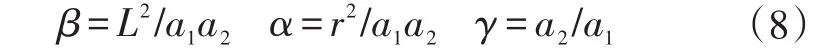
因此，通过设定α=1，两种模态的振动结点如同就分别发生在前、后轴处。结果，前轮处的激励就不会影响后轴处的车体，相反也是如此。对于这样的一辆车，车的前、后部分是相互独立的。因此，解耦条件α=1使得原本的2自由度系统变成了2个相互独立的单自由度系统。也就是说质量分配系数α越接近1车辆的跳动和俯仰越容易解耦。

2.3 线性悬架平顺性

前、后车轮走在同一车辙上，前、后悬架振动间的时间延迟是车辆轴距L和车速v的函数。在车辆后轮刚刚通过一个脉冲激励时，车辆处于俯仰最严重的状态[7-8]。为了建立一个有关平顺性的分析基础，可以将方程(4)、(5)写成[5-6]：

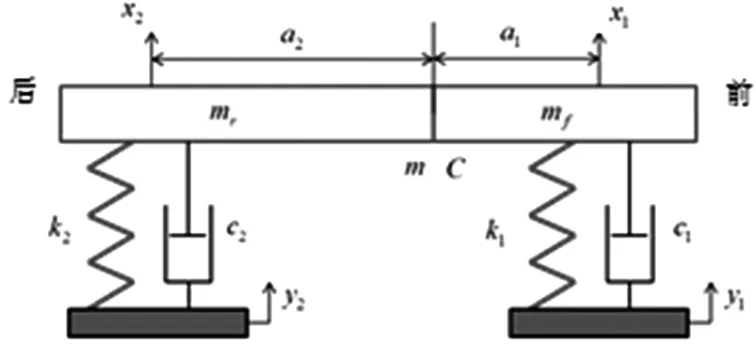
图1 简单2自由度车辆模型[5-6]

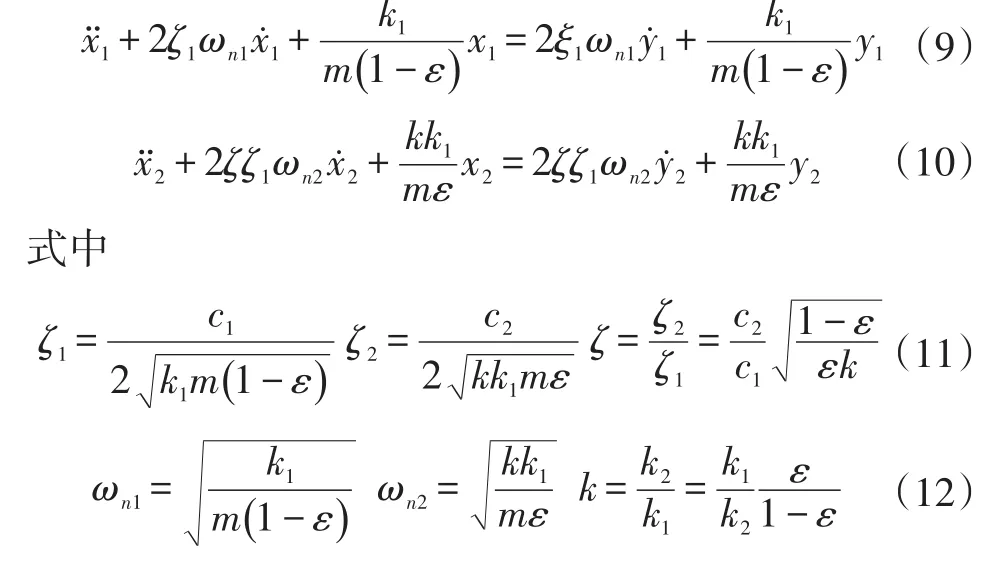
参数k为后/前弹簧的弹簧刚度比，ζ为后/前减振器阻尼比的比值。

为了达到平顺性很必要的一点是，后悬架系统必须振动得更快，并在合理的时间范围内赶上前悬架系统。即后悬架必须设计合适的参数和更高的频率，并在振动消失之前的某个合理时间点，达到和前悬架振幅相同。然后在车辆出现明显俯仰之前，系统的振动已经消失。

在路面设定为单位脉冲激励输入的条件下，求解方程（9）、（10）可得

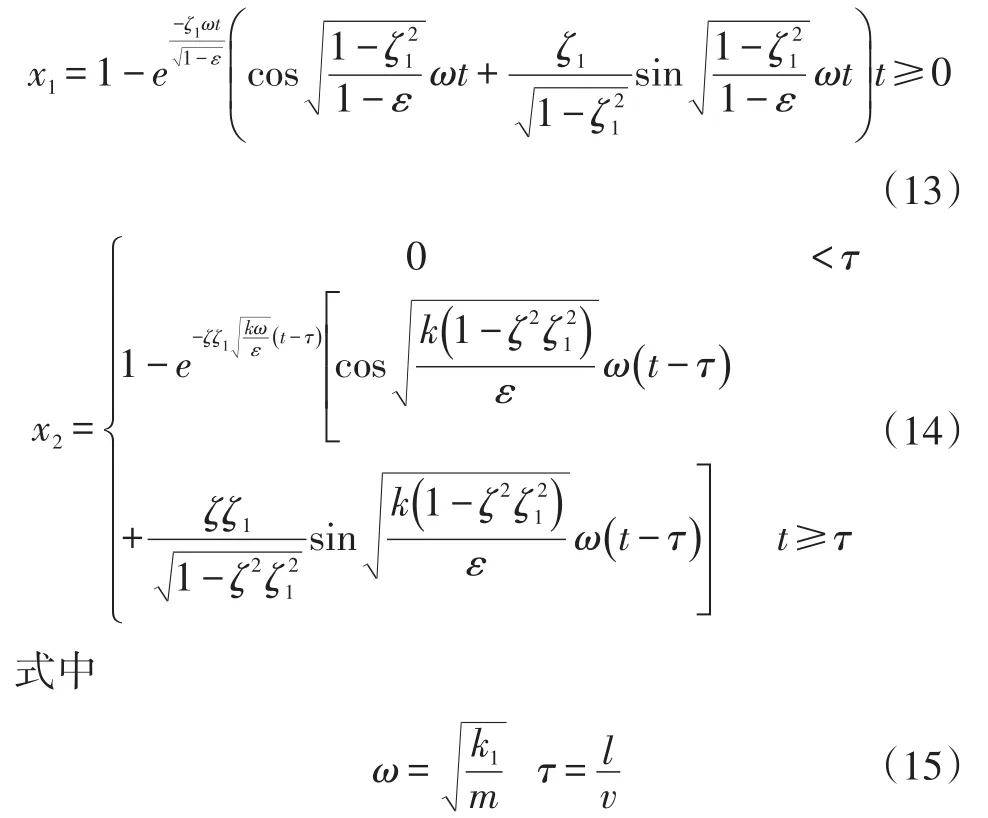
作为一个理想的追赶时间，需满足前、后悬架系统达到他们的第3个极值的时候振幅相同，时间相等。

x1的第3个极值出现的时间及此时相应的位移为：

方程（19）是与弹簧刚度比k无关的，求解可得减振器阻尼比的比值：

这说明了只有在前/后悬架的阻尼比相等的条件下，车辆前、后部在第3个极值时的位移才有可能相等。

通过方程（19）求解弹簧刚度比k可得：

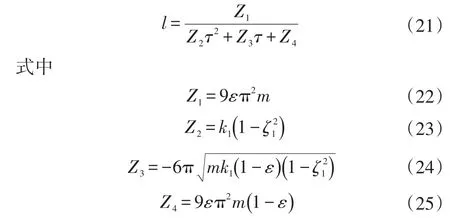
根据以上求得的公式，可以给出要达到近似平顺性的车辆的各参数之间需遵循的关系图。例如，考虑到0.4≤ε≤0.6可以覆盖所有的轿车的情况，图2表示了当ζ=0.5时，对于不同的ε的取值，k与τ之间应保持怎样的函数关系以达到近似平顺性。

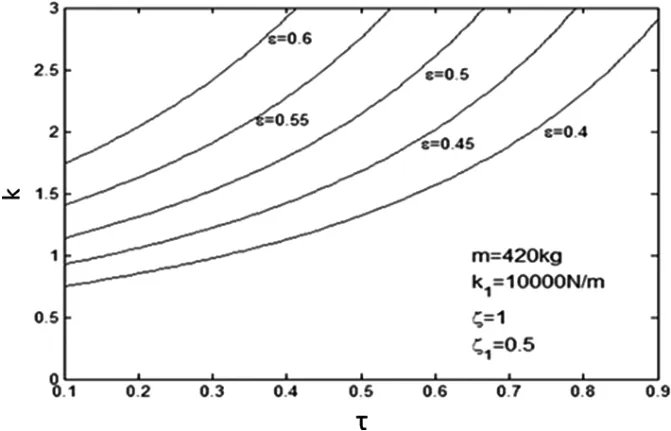
图2 当ζ1=0.5，0.1≤τ≤0.9时，τ与k的函数关系

3 某自主电动车设计案例

以某电动车为例，利用欧雷准则匹配前、后悬架刚度和阻尼，优化整车平顺性，所需整车参数如表1。

3.1 某电动车前悬架偏频目标设定

企划部门给定本电动车的特征目录中舒适性性能定位为细分市场最好（Best In Class,BIC），结合表2的主客观对标结果及性能指标数据库中得出的性能目标发展趋势，综合以上并根据所开发的电动车型载荷、轴距等信息设定所开发车型的前偏频目标为1.215 Hz（图3），则计算的前悬架刚度为k1=24.72 N/mm。

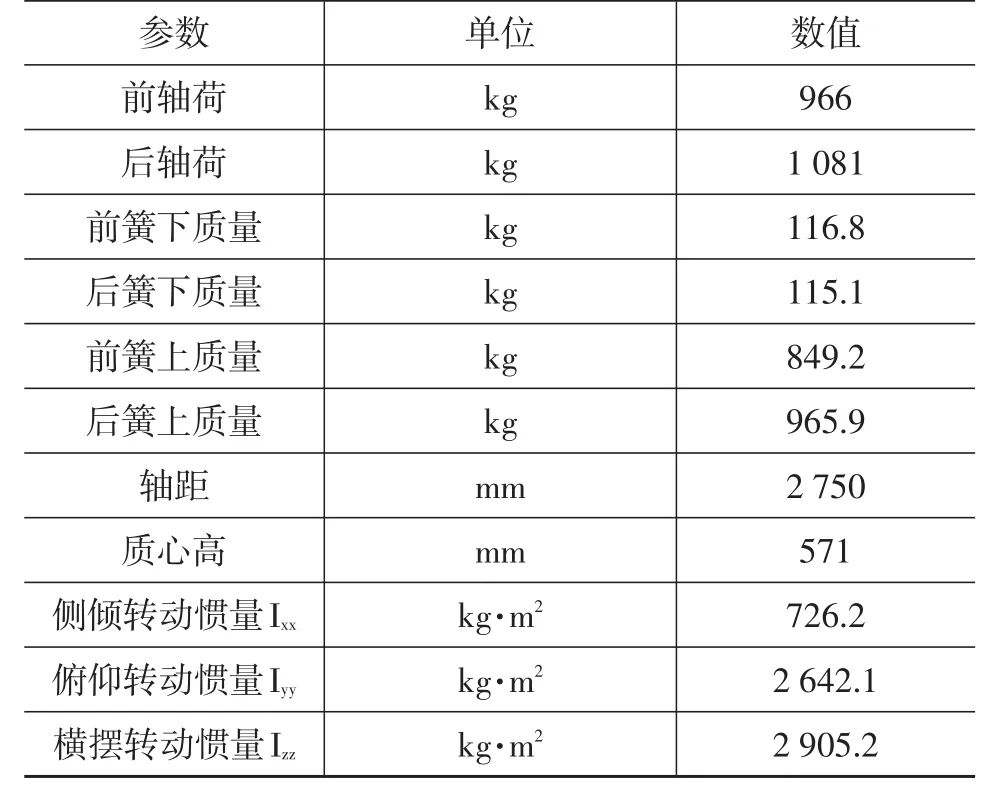
表1 某电动车设计参数

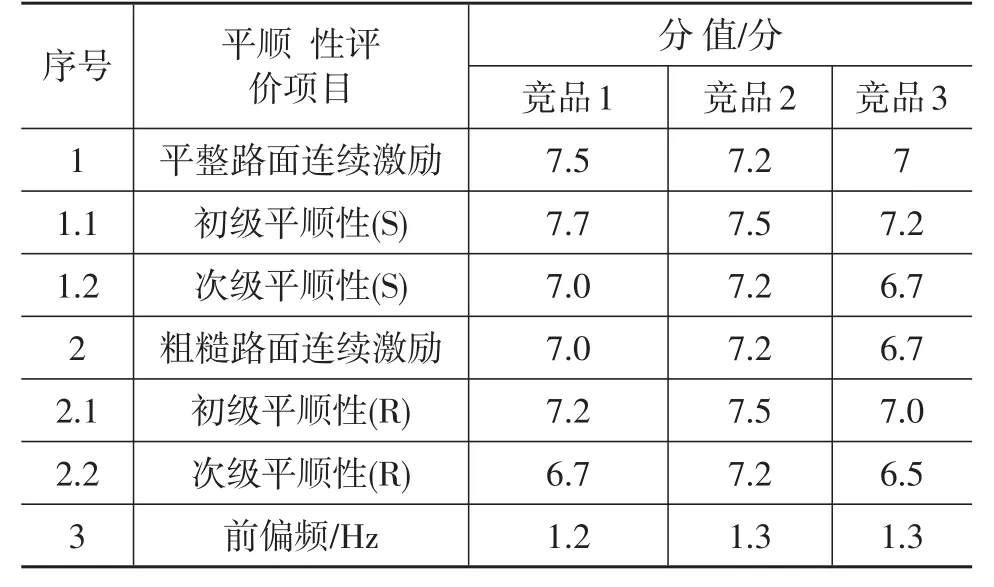
表2 某电动车对标结果(悬架刚度匹配相关)

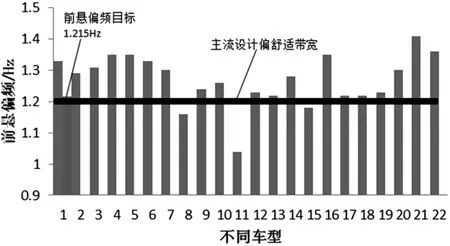
图3 前偏频目标设定

3.2 基于上述准则理论的某电动车前后悬架刚度匹配

对于本电动车来说，据式(3)ε取0.511 1。

主观评价标准规定在进行悬架俯仰特性主观评价过程中的车速为50 km/h至最高车速。根据前面的理论分析可得，某电动车k与τ的函数关系，如图4，最终计算得到后悬架在不同车速下的最佳匹配刚度如表3所示。

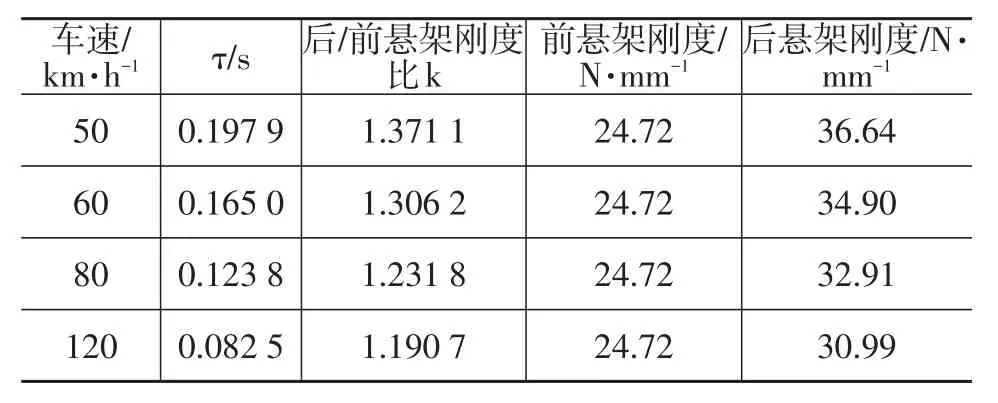
表3 某电动车不同车速前后悬架刚度匹配

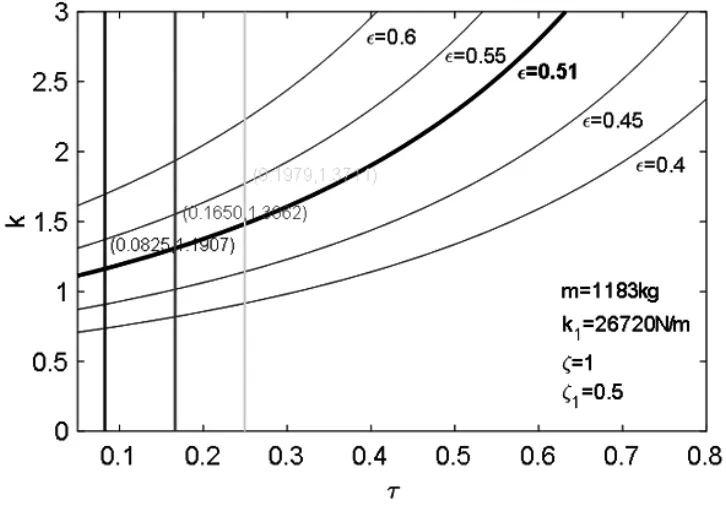
图4 某电动车k与τ的函数关系

常用车速60 km/h,故后悬架刚度匹配初步选择34.90 N/mm。

3.3 某电动车动力学性能调校结果及验证

车辆调校选用不同的前后弹簧刚度匹配最终根据初级平顺性的表现选定了最优方案。此方案前后悬架刚度试验测试结果如图5，主观评价结果(图6)来看匹配效果良好达到了开发目标，在弹跳（Bounce displacement）和俯仰（Pitch balance）方面均表现良好。

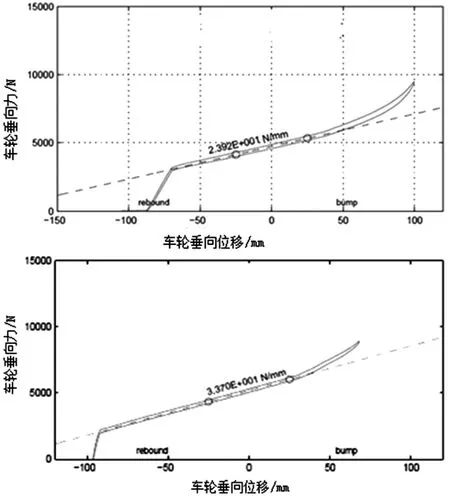
图5 某电动车最终前、后悬架刚度匹配试验结果

计算方案与最终调校方案二自由度模态振型对比结果，见图7。从表4可以看出，最终调校方案前后悬架刚度匹配与前期设计值偏差小于6.2%，可以缩小调校的刚度范围，从而减少调校件方案，减少开发成本，缩短开发周期。

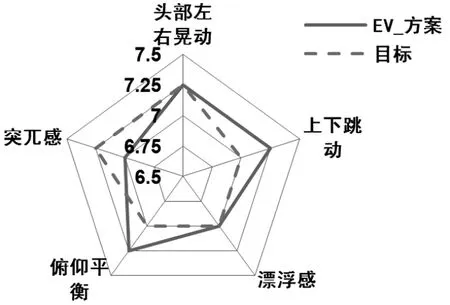
图6 某电动车初级平顺性最终调校及评价结果

图7 计算方案与调校方案二自由度模态振型对比结果

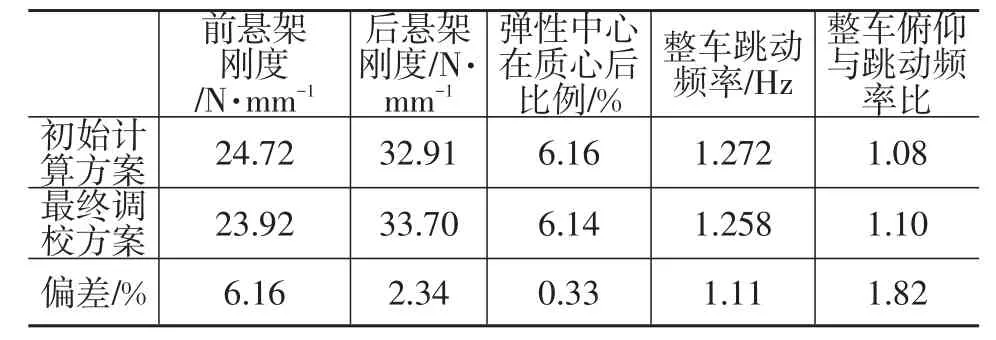
表4 某电动车计算与调校结果对比

4 结论

对由实验总结出来的欧雷准则进行了理论分析及工程应用推导，并应用在某款纯电动汽车动力学性能的开发过程中，通过实车验证来看，前期分析设计可以很接近的对前后悬架刚度进行匹配，该方法不仅能够缩短调校周期满足开发需求具有实际的工程指导意义，同时也发现按准则跳动频率比俯仰频率低1.2倍，而最终实车调校后最优方案为1.1倍，下一步将考虑对悬架阻尼特性匹配结合起来并对欧雷准则经验总结的相关数值进行修正，以便开发前期更精准的对平顺性进行性能设计控制，缩短调校周期。