钢筋混凝土双连梁剪力墙结构受力性能分析

季海峰

(山西省建筑科学研究院有限公司，山西 太原 030001)

0 引言

连梁是剪力墙结构中墙肢传力的重要联系构件，其具有一定的强度、刚度及变形能力，对整体墙肢承载力及抗震性能影响较为显著。在建筑结构设计中，由于连梁的约束作用，使得墙肢具有足够的刚度及承载力，在地震发生时，连梁常作为第一道防线首先屈服，在梁端部产生塑性铰，进而增加结构的阻尼性能。然而在实际工程设计中，连梁抗剪承载力常常不满足要求，需要采取一定措施降低连梁内力。在诸多方法中，较为理想的当属双连梁结构体系[1-3]。

近年来，双连梁体系受力性能也得到了较多研究。朱炳寅[4]对双连梁等效计算问题展开研究，提出抗弯刚度等效及抗剪截面面积等效两种方案。李奎明等[5]通过试验对高性能混凝土双连梁剪力墙展开研究，探讨不同连梁形式对结构承载力、延性及耗能能力影响，研究证实了高性能混凝土双连梁剪力墙具有良好的抗震性能。丁永君等[6,7]对高强钢筋高强混凝土双连梁结构展开研究，结果表明双连梁结构延性及耗能性能更好。姜忻良等[8]对提出双连梁与单连梁转角刚度等效的方法，并基于有限元分析验证了该方法的有效性。陈云涛[9]对双连梁几种等效原则进行了分析，并与实际计算结果展开对比。曹杨等[10,11]对双连梁短肢剪力墙结构随机损伤演化过程展开研究，分析了结构受力过程中均值、方差及变异系数变化规律。胥玉祥等[2]对双连梁受力性能展开分析，结果表明双连梁方案可以显著降低连梁内力，有利于改善高层建筑受力性能。

本文研究旨在基于上述已有研究成果，基于有限元数值模拟进一步对双连梁剪力墙结构体系受力性能展开研究，对比不同连梁形式剪力墙结构的破坏形态、承载力、延性变化特点，为双连梁剪力墙结构体系设计应用提供相应参考。

1 计算模型

1.1 模型尺寸及配筋

本文选取三层联肢剪力墙作为计算模型，分别建立单连梁的联肢剪力墙结构计算模型SW-1和双连梁的联肢剪力墙计算模型DW-1。为提高计算效率，模型计算时采用缩尺模型，具体模型尺寸如图1所示。模型中，墙体总高度为2 200 mm，墙体厚度为100 mm，两侧墙肢长度为600 mm，中间连梁宽度为400 mm。SW-1中连梁宽度为100 mm，高度为250 mm，连梁箍筋为φ6@80，纵筋为4φ12，腰筋为2φ8；DW-1中连梁宽度为100 mm，高度为120 mm，连梁箍筋φ6@80，纵筋为4φ8。墙肢竖向钢筋为双层φ6@80，水平钢筋为φ6@80。墙肢两侧暗柱截面尺寸为100 mm×100 mm，纵筋为4φ8，箍筋为φ8@80。混凝土强度等级为C45，墙体轴压比为0.15。

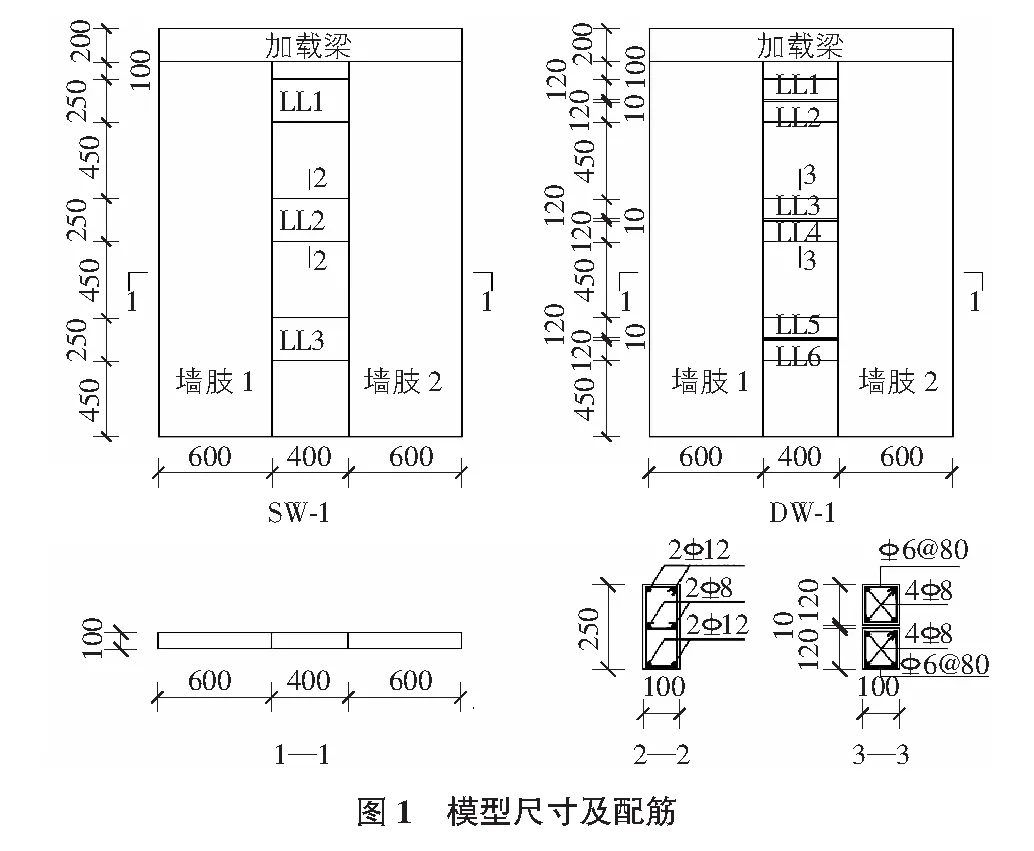
1.2 材料模型

钢筋的应力—应变关系采用理想弹塑性模型，在ANSYS有限元分析时，采用双线性等向强化模型BISO，钢筋屈服强度fy=300 MPa，弹性模量ES=2.0×105MPa，泊松比νs=0.3。

混凝土强度等级为C45，轴心抗压强度fc=29.6 MPa，轴心抗拉强度ft=2.51 MPa，泊松比νc=0.2。采用弹塑性本构关系，混凝土应力—应变关系参照《混凝土结构设计规范》[12]给出的计算式，如下所示：

(1)

(2)

其中，n为方程上升段参数；α为方程下降段参数；fc为混凝土轴心抗压强度；εc为混凝土峰值应变。

依据上述关系，建立混凝土应力—应变关系见图2。

1.3 有限元模型建立

钢筋混凝土结构有限元分析时通常有三种建模方式，即整体式、分离式、组合式。在ANSYS分析中，通常采用整体式和分离式，本文分析中采用分离式模型，即将结构中钢筋及混凝土采用不同的单元处理。模型中，混凝土采用Solid65单元，该单元可以很好的模拟混凝土的开裂和压碎；钢筋采用Link8单元。建立模型时，不考虑钢筋与混凝土的粘结滑移，钢筋与混凝土单元共用节点。三层联肢剪力墙SW和DW有限元模型如图3所示。

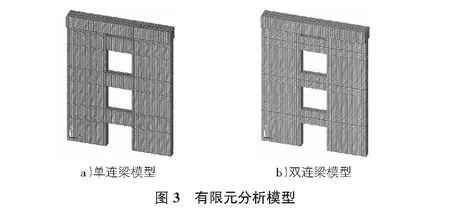
1.4 荷载

模型建立后，对模型底部施加固定约束。在模型加载梁顶面施加均布荷载，使得墙肢轴压比为0.15。在加载梁左侧逐步施加水平荷载，加载子步为10 kN，直至结构破坏。

2 有限元计算结果分析

2.1 荷载位移曲线

在往复加载作用下，获得单连梁和双连梁模型的荷载—位移骨架曲线如图4所示。从图4对两种剪力墙模型的骨架曲线分析可知，在加载的初始阶段，随着位移的增大，荷载迅速增加，荷载与位移呈现线性增大，呈现出明显的弹性特征；此后，随着位移的进一步增加，位移增大幅度逐渐放缓，试件逐渐达到屈服状态，荷载增速开始放缓，曲线的斜率逐渐降低，直至曲线进入下降段。

2.2 承载力及延性系数

单连梁剪力墙模型和双连梁剪力墙模型数值模拟计算结果如表1所示。从表1数据可知，双连梁剪力墙的屈服位移、峰值位移、极限位移较单连梁剪力墙提升11.8%～30.2%，双连梁剪力墙的延性系数较单连梁剪力墙有所提高；双连梁剪力墙的屈服荷载较单连梁剪力墙下降25.7%，双连梁剪力墙的峰值荷载较单连梁剪力墙下降19.5%。可见，采用双连梁剪力墙模型后，结构构件的承载能力出现下降，但同时其延性得到提高。

表1 单连梁剪力墙和双连梁剪力墙荷载、位移及延性系数

2.3 裂缝发展及破坏形态

通过调阅不同受力阶段，单连梁和双连梁剪力墙裂缝发展情况，可知单连梁与双连梁的裂缝发展及破坏过程较为相似。此处以单调加载的单连梁裂缝发展及破坏过程为例，阐述模型裂缝发展及破坏过程。

图5所示为单连梁剪力墙在开裂荷载、屈服荷载及极限荷载三个阶段模型裂缝分布情况。从裂缝发展过程可知，随着荷载的增加，初始裂缝首先在二、三层连梁两个对角位置出现，此后左侧墙肢和右侧墙肢的底部先后开始产生裂缝。此后，上述裂缝均不断扩展，直至连梁和墙肢的纵筋相继屈服，左侧墙肢底部混凝土开始出现压碎，整体模型逐渐进入极限承载阶段，直至结构出现破坏。

3 结语

1)本计算中，在往复加载作用下，单连梁和双连梁剪力墙模型的荷载—位移骨架曲线变化趋势基本相同，均分为弹性阶段、屈服阶段和极限阶段。

2)本计算结果表明，双连梁剪力墙的屈服位移、峰值位移、极限位移较单连梁剪力墙提升11.8%～30.2%，表明双连梁剪力墙模型有着较好的延性及变形能力；双连梁剪力墙的屈服荷载较单连梁剪力墙下降25.7%，双连梁剪力墙的峰值荷载较单连梁剪力墙下降19.5%，表明采用双连梁的剪力墙模型承载能力有所下降，在结构设计中应考虑此类因素的影响。

3)本计算结果表明，单连梁与双连梁的裂缝发展及破坏过程较为相似，初始裂缝首先在二、三层连梁两个对角位置出现，此后左侧墙肢和右侧墙肢的底部先后开始产生裂缝，直至连梁和墙肢的纵筋相继屈服，左侧墙肢底部混凝土开始出现压碎，整体模型逐渐进入极限承载阶段。