基于遗传算法的散货船配载软件的开发
2020-05-05薄志斌
薄志斌,胡 义
(武汉理工大学 能源与动力工程学院,湖北 武汉 430063)
0 引言
传统的配载方案一般是由大副或港口工人通过经验凭借手工方式完成,这样的配载方案一方面耗时耗力,另一方面由于人工的疏忽会出现计算偏差。船舶货运量的大幅增加和航次路线的越来越复杂,使得传统方案越来越不适合当今的发展趋势[1]。
国外,早在20世纪90年代中期就开始研究散货船的配载并在计算机上开发相关的配载软件,其中:德国的SCHIFFKO公司开发了基于DOS环境的船舶计算软件;挪威的Autoship Systems Corporation公司开发出一款名称为Autoload的船用装载仪[2]。国内,大连海事大学史国友教授分析了货物在散货船的实际装载情况,建立约束条件,然后用静水力数据开发出散货船配载仪。另外,还有福海船舶配载仪,这是一款涵盖了谷物稳性计算和破舱稳性计算等很多实用功能的装载软件。
为此,从20世纪90年代起,散货船的配载优化和自动化配载就已经成为了相关领域内的研究热点。随着计算机的广泛应用,关于船舶配载的软件也慢慢开始出现,可以通过手动输入船舶的一些参数来完成配载的计算,但是这种配载方案仍然需要人工的干预调整,才能计算出最优的结果。近几年来随着人工智能的不断发展,该技术也逐渐在航海领域得到了广泛的应用,散货船的智能配载研究就是人工智能在航运业上的一种重要应用。智能化的配载方案不仅可以提高船舶在航行过程中的稳性和强度等,有利于船舶的运输安全,并且还会提高配载效率,降低船舶的运营成本[2]。本文从当前的配载软件市场出发,引进遗传算法对散货船配载进行研究,主要对配载系统中的约束条件从适应度缩放、模拟退火拉伸、加入精英保留法三个方面对配载系统进行研究。
1 散货船的遗传算法优化
1.1 遗传算法的主要操作
遗传算法的基本操作步骤:选择(Selection)、交叉(Crossover)和变异(Mutation)。遗传算法的执行中有编码操作和译码操作,其中编码操作就是将表现型转换到基因型,从基因型转换到表现型被称为译码操作。遗传算法在进行分析的时候只是将一个种群看作是一个对象来对其进行分析,然后进行编码、计算适应值、遗传操作和筛选等步骤,这几个方式都赋予了遗传算法一定的优势[3]。遗传算法实现的基本流程见图1。
1.2 程序设计流程
遗传优化程序的基本流程见图2。从图2可知,通过船舶基本参数来确定散货船的浮态和强度。为了满足散货船的约束条件,保证船舶在运营中的安全性,要对遗传算法的参数进行限制。
1.3 遗传编码的确定
编码是设计遗传算法的一个关键步骤,编码的好坏将直接影响到遗传算法后面的选择、交叉、变异等操作步骤。遗传算法的一大难点就是选择一个合适的编码方案,针对一个具体的应用问题时,首要目标就是找到其编码方案[4-5]。
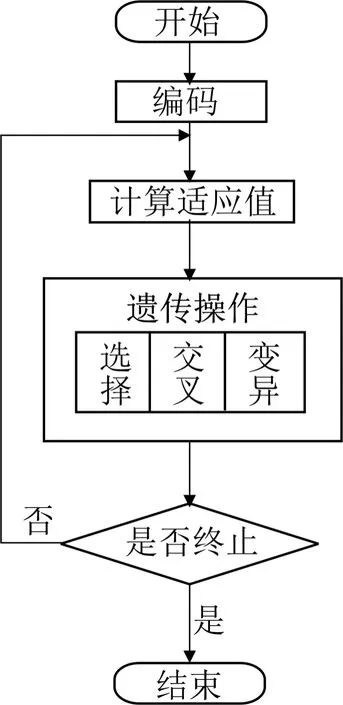
图1 遗传算法基本流程
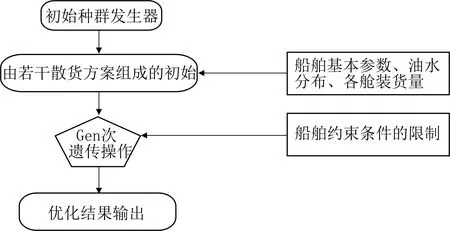
Gen—遗传的代次。
本文研究的76 000 t远洋散货船共有7个货舱,本次遗传算法优化采用两轮装货的编码方案。
随机产生的初始解有可能出现强度或者稳性不合格的情况,为此对遗传算法的初始解进行改进,可以采用第一轮装入货舱预计装载量的1/2。
2 散货船配载系统对约束条件的处理
基于遗传算法的配载系统约束条件主要包括以下4点:
(1)艏艉吃水在散货船装货过程中的任意状态下都不允许超过装货港的限制。
(2)船舶吃水差在散货船装货过程中的任意状态下都要在限定范围之内。
(3)各个校核点的剪力占该处剪力许用值的百分比不超许用值,且尽量小。
(4)初稳性满足规范要求。
对于不满足上述4个约束条件中任何一个条件的个体,装载仪软件中的约束条件函数会自动将其剔除出当前种群。
具体的操作步骤是:散货船配载对种群进行适应度计算时,对上面的4个约束条件依次进行初始判断,不符合的个体直接淘汰,并将其适应度f强制清零。符合的个体才依次进行其他操作,所以这些不能满足约束条件要求的个体将无法被遗传到下一代[6]。
2.1 适应度的缩放
遗传算法中适应度对最终的优化结果有直接的影响,所以对适应度的选择是极其重要的。一般遗传算法的适应度是固定不变的,但是这样存在着一些缺点。固定的适应度可能使早期种群中优秀的个体大部分都可以进入下一代,不仅会带来早熟的现象,而且会使种群的多样性受到影响,不能将早期较差个体中含有的部分优秀基因展示出来。这时,就需要采用适应度的缩放。早期适应度较低,能充分发挥每个个体中的基因作用;后期将适应度放大,扩大优秀个体之间的差异,从而能更好地得出最优解。
f′=af+b
(1)
式中:f′为缩放后的适应度;f为原来的适应度;a、b为系数。
2.2 模拟退火拉伸
Pau1 L.Stoffa提出了模拟退火拉伸。可以将此应用于遗传算法当中,使遗传算法具有适度的拉伸作用。
(2)
式中:fi为第i个的个体适应度;n为种群个数总数;g为遗传代数序号;T为温度;T0为初始温度。
采用模拟退火拉伸,目的在于使早期的个体在温度高时产生后代的概率相差不大,充分保障了种群的多样性。当遗传后期温度下降后,拉伸作用将越来越明显,使优秀的个体同普通个体拉开差距,从而获得遗传算法的优秀解[7]。
2.3 加入精英保留法
Grefenstette提出了精英保留策略。由于遗传算法的包容性,可以在本次配载当中加入精英保留策略。遗传算法中使用精英保留策略的主要目的就是为了使群体当中最优的个体不至于被淘汰,虽然最优的个体进化到下一种群的概率是很高的,但是以防万一,最保险的就是将其直接复制到下一个种群当中,百分百概率保留,并将新种群当中随机的一个种群个体或者最差的一个种群个体淘汰。这样进行操作可以帮助遗传算法优化的速度加快,并且保障了最优解的存在[8]。
3 软件开发
结合上面理论知识,用C++语言在Windows环境下完成装载仪在遗传算法下进行货物配载的开发工作。装载仪编码程序中构建遗传算法的个体和种群两个类,其中个体对应Individual,Generation对应种群。
(1)定义Individual类包括的成员变量和成员函数
设置个体染色体字符串、个体适应度和各舱第一轮的装货量的代码和相应操作的代码。
成员变量:Bool m_chrom[]
//个体染色体字符串
Float m_fitness
//个体适应度
Int m_xl~m_x7
//1~7轮的装货量
成员函数:Void Initial()
//初始化
Void GetX()
//解码
Float Getiftness (int x1,int x2,int x3,int x4,
int x5,int x6,int x7)
//返回个体适应度
Void Update()
//更新
(2)定义Generation类包括的成员变量和成员函数
设置遗传算法中父代种群、子代种群、种群中最优个体、最优个体的适应度、最优装货顺序的代码和相应操作的代码。
成员变量:Individual m_oldpop[]
//父代种群
Individual m_newpop[]
//子代种群
Individual m_bestone
//最优个体
Float m_bestiftenss
//最优个体适应度
Floatm_bestsequenee[]
//最优装货顺序
成员函数:VoidGeneration()
//构造函数
Int select
//选择
Void Crossover(int ml,int m2)
//变异
Void Mutation(bool child[])
//遗传
Void Generaiton()
//遗传操作函数
散货船配载软件的系统流程图见图3。
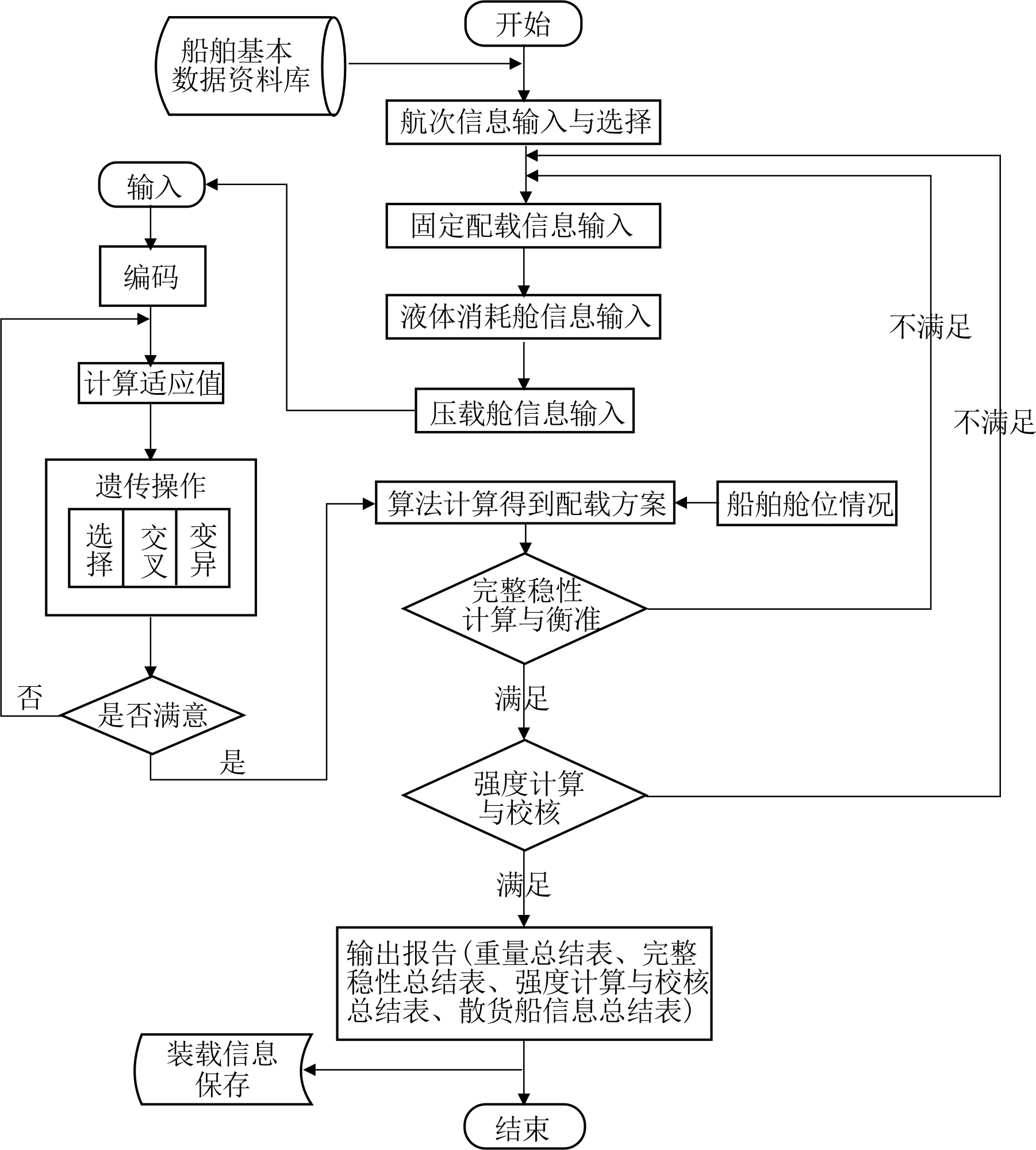
图3 软件流程图
3.1 产生初始种群
利用计算机的随机生成功能,连续随机产生28位二进制数据,这个二进制数即是散货船的一个初始个体。这个28位的二进制字符串对应个体的染色体,其中:1~4位对应的散货船1号舱经过第一轮装货后的舱内货物量,5~8位是对应散货船2号舱经过第一轮装货后的舱内货物量,以此类推。
初始种群是由初始个体组合而成的,可以用图4来表示初始种群的生成过程。图中:M为种群规模,字符串b=1000100010001000100010001000。

图4 初始种群产生流程图
本课题研究的是“76 000 t散货船”,将散货船的基本数据输入装载仪中,对遗传算法的初始解进行改进,可以将总载货量均匀分配作为初始解。1~7舱的装货量均为7 974.516,输入装载仪的货舱装载框中,见表1。表中:ρ为密度,Per为货物所占舱室的体积比,W为货物重量,H为货物高度,LCG为重心纵向坐标。
装载仪根据货舱输入框中的数据生成初始配载图,具体内容见图5,其中:X1~X7分别代表1~7舱的装货量。
计算散货船在初始配载状况下的船舶强度和稳性是否满足要求。通过装载仪算出“76 000 t散货船”在改进初始配载下的强度和稳性。散货船强度计算结果见图6,稳性计算结果见图7。
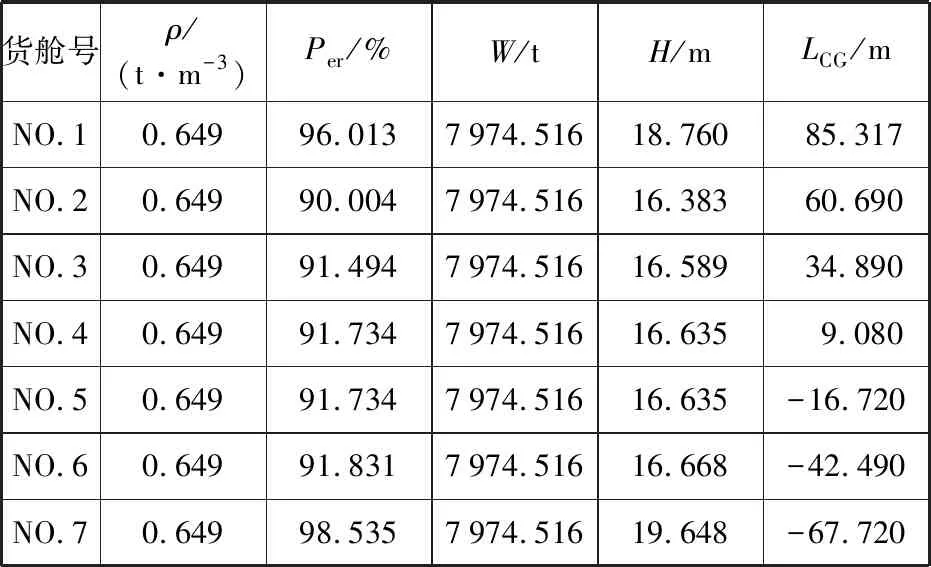
表1 初始解的货舱输入
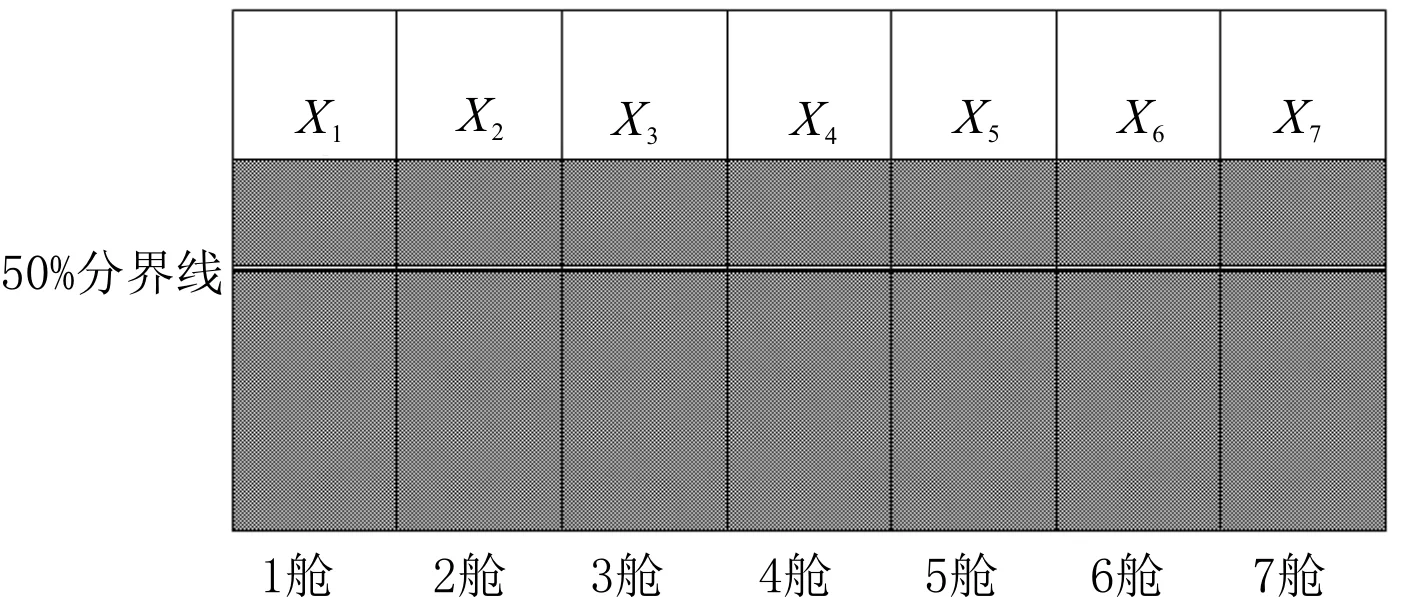
图5 初始配载图

图6 初始解强度计算结果
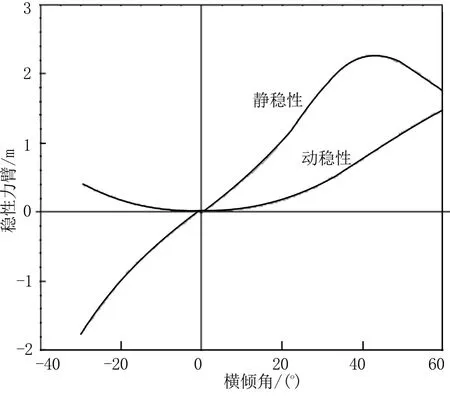
图7 初始解稳性计算结果
3.2 遗传算法的变异实现
经过初始装配后,用代码实现对个体的某些位置进行改变,将某些部位的二进制码从1变成0或者从0变成1,形成新的种群个体。将船舶的初始配载量进行变异操作,得到变异后的1~7舱的装货量为7 216.393、8 610.586、7 310.325、8 010.546、7 410.546、6 408.331、7 644.128,然后将变异后的装货量输入装载仪中。装载仪根据货舱输入框中的数据生成变异配载图,见图8,其中:X1~X7分别代表1~7舱的装货量。
计算散货船在初始配载状况下的船舶强度和稳性是否满足要求。通过装载仪算出“76 000 t散货船”在变异配载下的强度和稳性。散货船强度的计算结果见图9,稳性计算结果见图10。
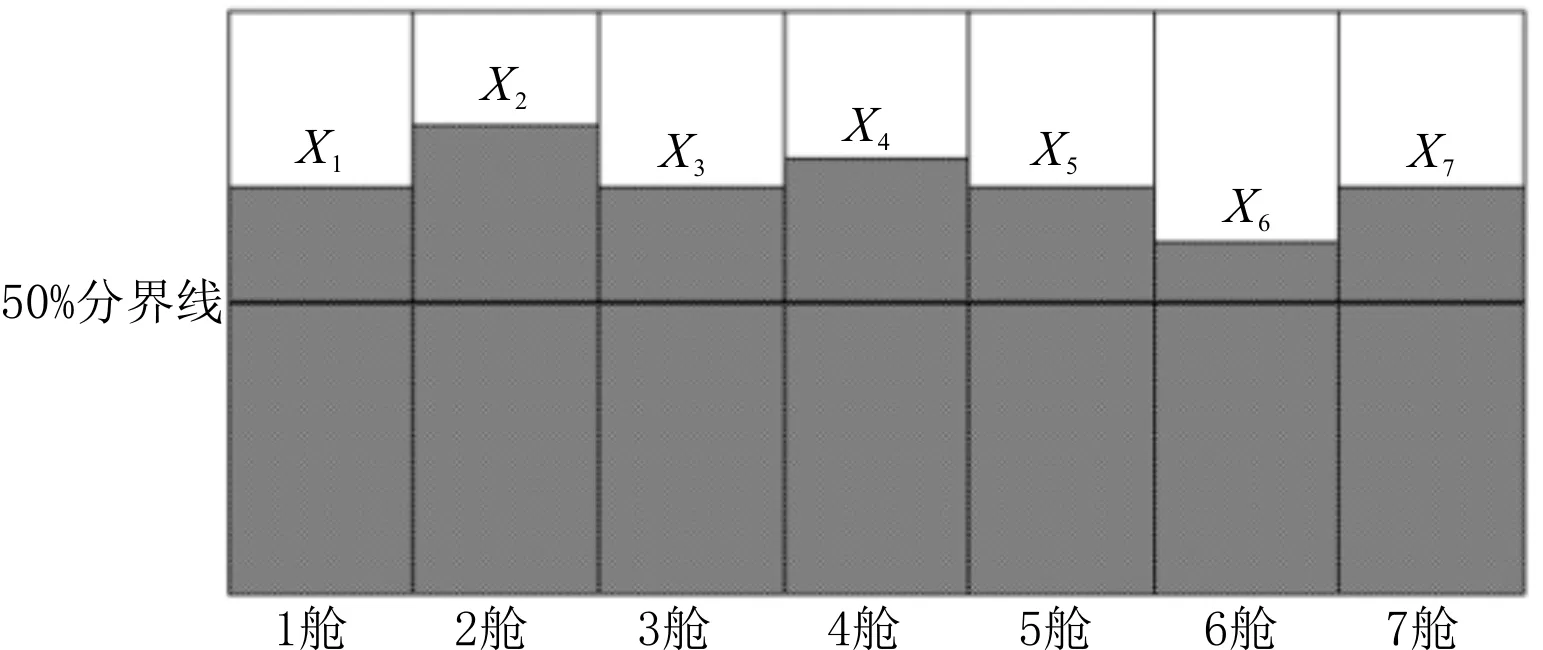
图8 变异配载图
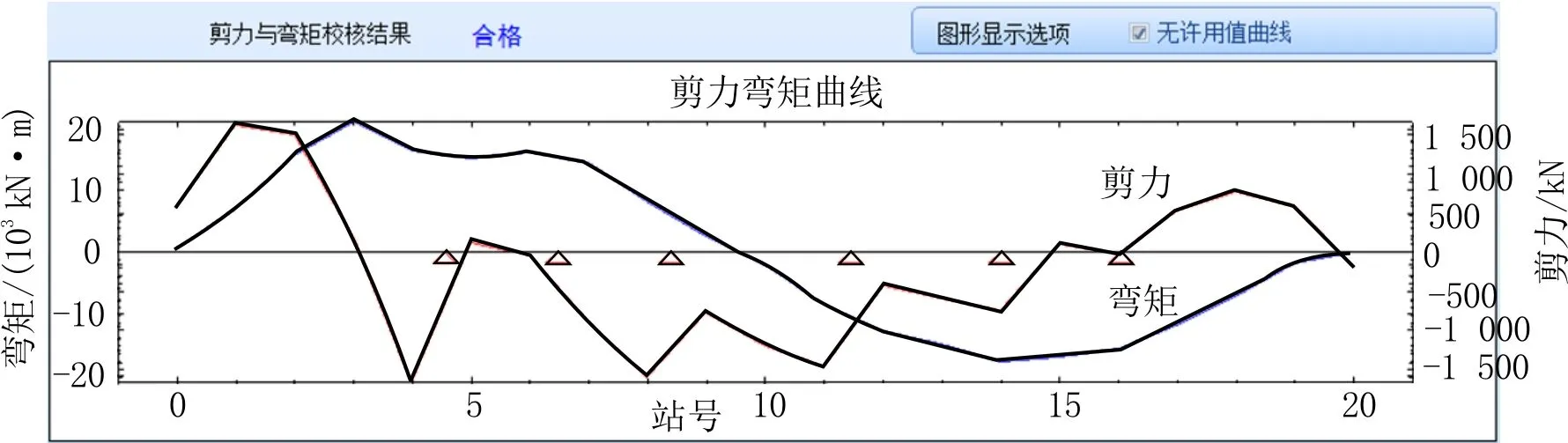
图9 变异强度计算结果
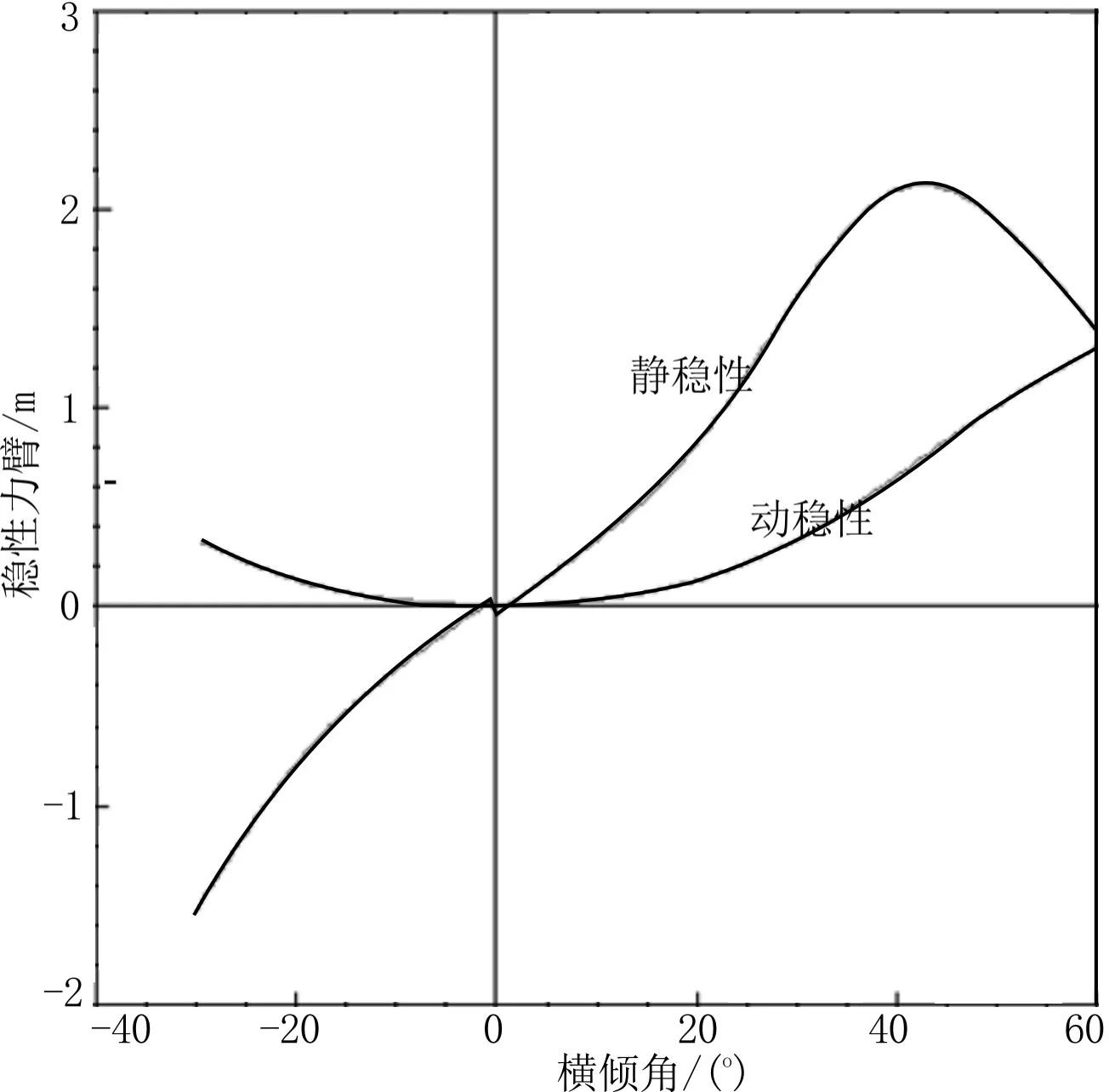
图10 变异稳性计算结果
3.3 散货船的最终配载完成
散货船配载经过上面的变异操作后,接下来需要进行交叉算法实现。交叉算法的主要步骤是:
(1)找到散货船配载交叉算法的起始点。
(2)对散货船配载进行交叉操作。
(3)去除交叉之后的雷同信息。
经过初始装配和变异装配后,进行最后的交叉操作。通过计算机运算得到1~7舱的最优装货量,其装货量分别为8 040.393、7 500.558、7 927.325、8 710.546、7 422.546、6 906.331、8 244.128,将最优解装货量输入装载仪中。装载仪根据货舱输入框中的数据生成变异配载图,见图11,其中:X1~X7分别代表1~7舱的装货量。
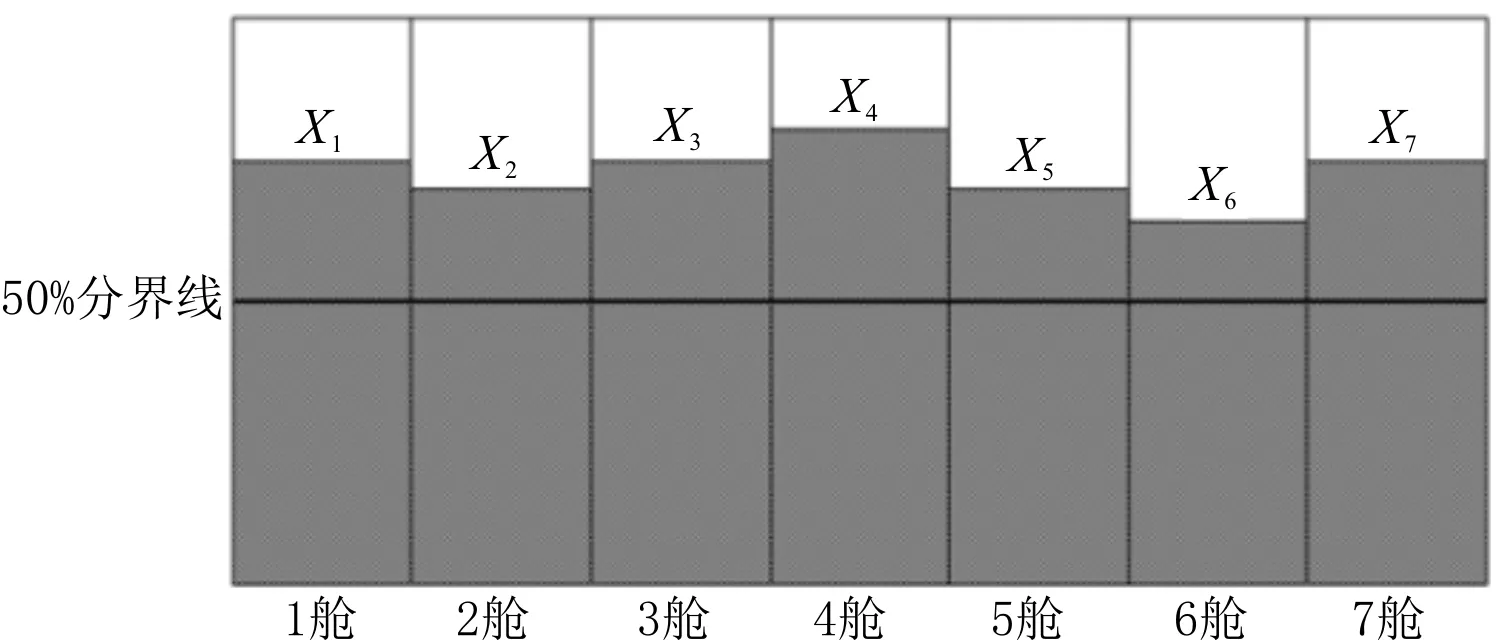
图11 最优解配载图
计算散货船在初始配载状况下的强度和稳性是否满足要求。通过装载仪算出“76 000 t散货船”在最优解配载下的强度和稳性。散货船强度计算结果见图12,稳性计算结果见图13。
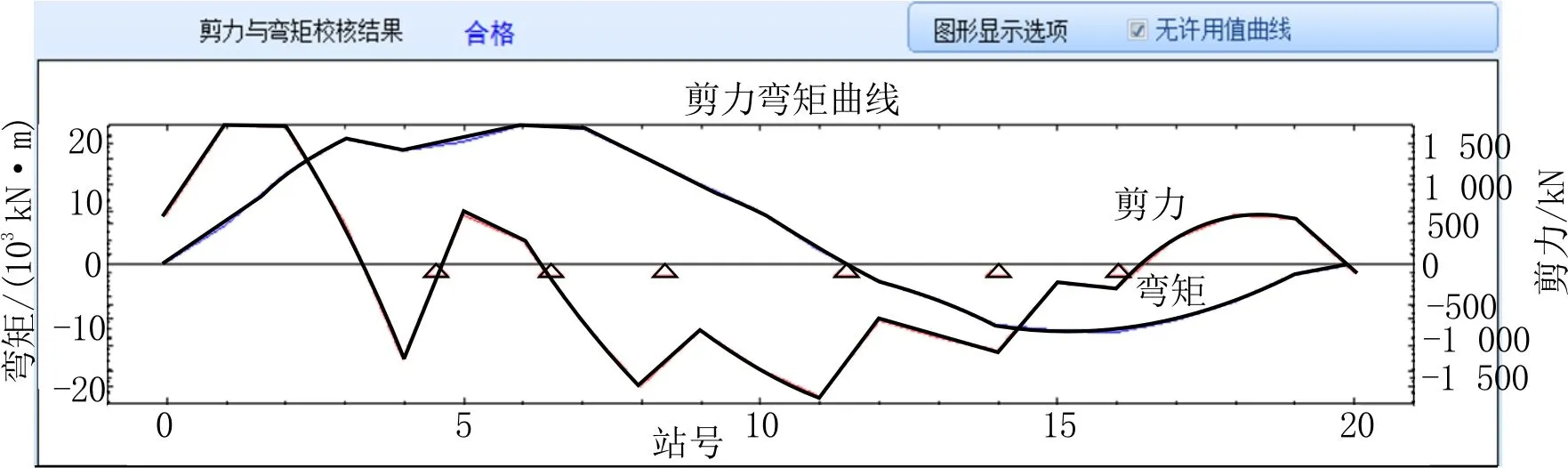
图12 最优解强度计算结果
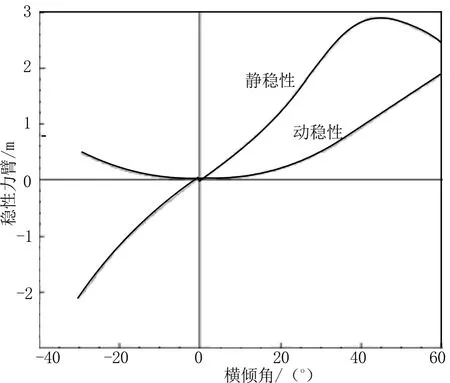
图13 最优解稳性计算结果
从图6、图9、图12中找出初始解、变异解、最优解的剪力许用值比例的最大值和弯矩许用值比例的最大值,其结果见表2。
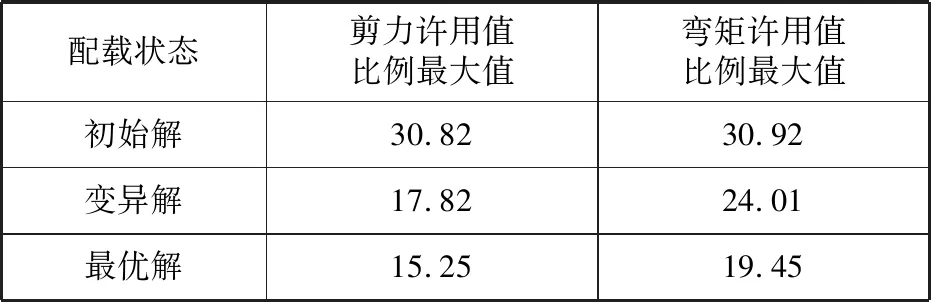
表2 强度计算结果对比
从表2看出,最优解下的剪力和弯矩许用值比例最大值表现最好,稳性没有明显的区别。经过遗传算法优化后的船舶配载方案表现更好,所以此算法有得到满意解的能力。
4 结语
散货船优化配载问题是一个多目标组合优化问题,本文采用遗传算法求解该问题。基于遗传算法,尝试求解在保证船舶安全航行的前提下,满足船舶的强度和稳性的最佳方案,但是限于问题的复杂性,研究过程做了大量的假设,在实际应用中有一定的局限性。
如今,我国大多数散货船码头仍然处于人工作业的状态,需要配载人员做出大量的工作。因此,对散货船配载的研究不管在理论还是实际上,都有着重要意义。
