交错立方体在故障情形下的诊断度和诊断算法*

王 喜，张书奎

(1.苏州工业职业技术学院,江苏 苏州 215004；2.苏州大学计算机科学与技术学院,江苏 苏州 215006)

1 引言

多处理器互连网络(简称互连网络)是指由多个处理器按照一定规则相互连接而成的网络，目前越来越广泛地出现在计算机技术的相关研究与应用领域中。作为并行系统的基础，互连网络的性质直接决定了系统的性能。近年来，我国在基于并行系统的超级计算机领域有一系列的重大突破，特别地，由国防科技大学牵头研制，安装在国家超级计算天津中心的超级计算机——“天河三号”E级原型机，在最新的全球超级计算机TOP500榜单中蝉联冠军[1]。

由于大规模互连网络中有很多处理器，这就很难避免某些处理器出现故障，而这些故障处理器可能影响到整个互连网络的稳定性，从而导致整个网络瘫痪，造成极大的经济损失。一个互连网络的拓扑结构可用一个图来表示，其中处理器与处理器之间的通信链路可分别用顶点集和边集表示。为了确保互连网络可以正常运行，那么在顶点出现故障时，就应及时、准确地找出故障顶点并进行替换。系统能够找出故障顶点并进行替换的能力，称为系统的诊断性。系统的诊断度是一个系统中能够准确找出所有故障顶点的最大个数。若系统中出现的故障顶点的个数不超过其诊断度t时，则该系统能够确保所有的故障顶点都可被正确地诊断出来，那么系统是t-可诊断的[2]。

Preparata等[2]在给出系统级故障诊断概念的同时提出了一个经典诊断模型——PMC诊断模型，该模型是用3位作者姓名的首字母来命名的。基于该诊断模型的研究已经在大规模多处理器系统、无线传感器网络系统、片上网络设计等领域广泛应用[3]。PMC诊断模型使用测试顶点测试其它顶点，且通过测试结果来判断顶点状态，然而，如果测试顶点本身是有故障的，那么测试的结果将是不准确的。Chang等[3]研究了判断一个网络是否适用 PMC诊断模型的方法。 Hakimi等[4]证明了一个系统在PMC模型下是可诊断的，还给出了系统在PMC模型下是t-可诊断的充分必要条件。Lin等[5]研究了基于PMC模型的通用正则图上限制连通度和诊断度之间的关系。然而，上述研究成果无法适用于大部分的网络[6]。因此，近年来，研究者们做出了大量关于特殊网络在PMC模型下的诊断度和t-诊断的研究成果[7 - 10]。曹骞等[8]研究了无K3子图的互连网络在PMC模型下的条件可诊断度。张丽果等[9]提出了PMC模型下超立方体的一种时间复杂度为O(N2)的条件诊断算法。

交错立方体(Cross-cube)[7]作为超立方体网络的一类重要变形，与超立方体相比具有低直径、哈密顿连通性等优越性。研究交错立方体中部分顶点和边出现故障的情形下的诊断度和诊断算法，能够更加精确地度量该网络的可性。本文将讨论交错立方体上存在故障边和故障顶点时，基于PMC模型的系统诊断度和诊断算法。进一步，将研究该算法的时间复杂度并进行相关仿真实验。研究结果表明，本文设计的算法在高效性方面明显优于文献[9]和文献[11]中的诊断算法。

2 预备知识

本文所用到的图的符号和定义遵循徐俊明[12]所著图论书中规范。本文使用G=(V(G),E(G))表示一个图， 其中V(G)表示顶点集，E(G)表示边集[12]。对于图G中任意2个顶点u和v，若(u,v)∈E(G)，则u和v是邻居；顶点u在图G中的邻居集合表示为NG(u)={v|(u,v)∈E(G)}；顶点u和v之间的距离表示为dist(u,v)；顶点u的度数表示为degG(u)。图G的最小顶点度数表示为δ(G)。如果V′⊆V(G)，可用G[V′]表示图G的顶点导出子图。进一步，使用G-V′来表示G[V(G)-V′]。 图G的连通度表示为κ(G)[12]。

Figure 1 A 4-dimensional cross-cube C4图1 1个4维交错立方体C4

在PMC诊断模型下，相邻的顶点可相互测试。给定图G中任意2个相邻的顶点u和v，顶点u对顶点v进行了1次测试可以表示为1个有序对〈u,v〉，其中u表示测试者，v表示被测试者，根据u和v的测试状态可得出相应的测试结果0或1。如表1所示，当且仅当测试者u是无故障的，才可以精确地给出被测顶点v的正确测试结果。例如若v是无故障的，则测试结果是0；若v是有故障的，则测试结果是1。若测试者u是有故障的，则对被测试顶点v的诊断结果是不准确的，测试结果可以随机为0或1。

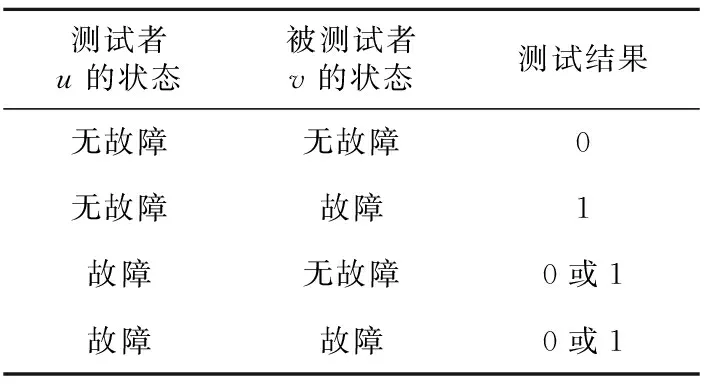
Table 1 PMC model表1 PMC诊断模型

1个图G中相邻顶点之间进行的所有测试所构成的集合，称作测试任务，可用1个有向图T=(V,L)表示，其中在测试任务T中u测试v用〈u,v〉∈L表示。本文假设任意2个相邻顶点会互相进行测试，即若(u,v)∈G，则有〈u,v〉∈L且〈v,u〉∈L。

测试任务T的所有测试结果的集合可表示为症候群，用函数σ：L→{0,1}来表示。给定任意测试任务T的1个症候群σ，故障顶点集合F⊆V，以及顶点u∈V-F，当顶点v∈F的测试结果为σ(〈u,v〉)=1，以及当顶点u∈V-F的测试结果为σ(〈u,v〉)=0时，则称F与σ是一致的。由于测试者出现故障时给出的测试结果是不可靠的，故同一个故障顶点集合F会产生出多个不同的症候群。本文使用σ*(F)来表示故障顶点集F所有可能产生的症候群。在图2的网络结构示例中，有4个顶点相连，其中u,x,y为无故障顶点，v是故障顶点。在PMC模型中，相邻的顶点都会进行相互测试，从而该网络产生测试任务T={〈u,v〉,〈v,u〉,〈v,x〉,〈x,v〉,〈x,y〉,〈y,x〉}。测试结果对应的症候群为σ*={{1,0,0,1,0,0},{1,1,0,1,0,0},{1,0,1,1,0,0},{1,1,1,1,0,0}}。

Figure 2 A diagnosis example of PMC model图2 PMC模型诊断案例

定义2[2]对于任意2个不同的故障顶点集合F1,F2⊂V，若满足条件σ*(F1)∩σ*(F2)=∅，则F1与F2是可区分的故障顶点集，(F1,F2)是1对可区分对；否则(F1,F2)是1对不可区分对。

定理1[3]对于任意2个不同的顶点集合F1⊂V和F2⊂V，F1和F2是可区分对的充分必要条件是V-(F1∩F2)至少存在1个顶点u与F1ΔF2(顶点集合F1和F2的对称差)中的1个顶点v相邻。

定理2[4]任意的图G=(V(G),E(G))在PMC诊断模型下是t-可诊断的充分必要条件是存在2个不同的故障顶点集合F1⊂V和F2⊂V是可区分的，且满足|F1|≤t和|F2|≤t。

定理3[13]若n≥2，则κ(Cn)=(n+1)。

定理4[7]若n≥3，则Cn是(n+1)-可诊断的。

3 交错立方体的诊断度

本节研究交错立方体的诊断度的精确值。首先，在引理1和引理2中证明Cn上顶点邻居集合的下界；接下来在引理3中研究Cn的可区分对；最后给出定理5和定理6，证明Cn的可诊断性和诊断度的精确值。

根据Cn的一些基本性质，可证明引理1成立。

引理1 给定u和v是Cn中2个不同的顶点，且(u,v)∈E(Cn)，则有|NCn(u)∪NCn(v)|≥2n。

证明 根据交错立方体的定义，在Cn中相邻的顶点最多有2个共同邻居。设E′={(u,v)|u=un-1un-2…u2u1u0,v=un-1un-2…u2v1v0},可分为以下2种情形：

情形1 当(u,v)∉E′时,则|NCn(u)∩NCn(v)|=0。由此可得|NCn(u)∪NCn(v)|=|NCn(u)|+|NCn(v)|-|NCn(u)∩NCn(v)|≥(n+1)+(n+1)-0=2n+2。如图3a所示。

情形2 当(u,v)∈E′时,则|NCn(u)∩NCn(v)|=2。由此可得|NCn(u)∪NCn(v)|=|NCn(u)|+|NCn(v)|-|NCn(u)∩NCn(v)|≥(n+1)+(n+1)-2=2n。如图3b所示。

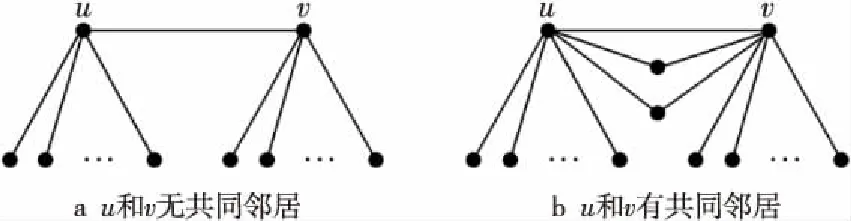
Figure 3 Examples of the verticesu,v and their neighbors in Cn图3 Cn中顶点u和v及其邻居的示例

根据上述情况，可得|NCn(u)∪NCn(v)|≥2n，引理1得证。

引理2 给定u，v和x是Cn上3个不同的顶点，且这些顶点满足如下2个条件：(1) (u,v)∈E(Cn)；(2)(v,x)∈E(Cn)。则有|NCn(u)∪NCn(v)∪NCn(x)|≥3n-2。

证明 根据交错立方体的定义，在Cn中相邻的顶点最多有2个共同邻居，且距离为2的顶点最多有2个共同邻居。令E′={(u,v)|u=un-1un-2…u2u1u0,v=un-1un-2…u2v1v0}以及W(u,v,x)= |NCn(u)∪NCn(v)∪NCn(x)|=|NCn(u)|+|NCn(v)|+|NCn(x)|-|NCn(u)∩NCn(v)|-|NCn(u)∩NCn(x)|-|NCn(v)∩NCn(x)|，可分以下5种情形：

情形1 当(u,v),(u,x),(v,x)∉E′且NCn(u)∩NCn(x)={v}时，则|NCn(u)∩NCn(v)|=|NCn(v)∩NCn(x)|=0且|NCn(u)∩NCn(x)|=1。那么W(u,v,x)≥3(n+1)-0-0-1=3n+2。

情形2 当(u,v)∈E′且(u,x),(v,x)∉E′，则|NCn(u)∩NCn(v)|=2×|NCn(v)∩NCn(x)|=0且|NCn(u)∩NCn(x)|=1。那么W(u,v,x)≥3(n+1)-0-2-1=3n。

情形3 当(x,v)∈E′且(u,v),(u,x)∉E′，与情形2类似，有W(u,v,x)≥3n。

情形4 当(u,v),(u,x),(v,x)∉E′且|NCn(u)∩NCn(x)|={v,y}时，则|NCn(u)∩NCn(v)|=|NCn(v)∩NCn(x)|=0且|NCn(u)∩NCn(x)|=2。那么W(u,v,x)≥3(n+1)-0-0-2=3n+1。

情形5 当(u,v),(u,x),(v,x)∈E′时，与情形4类似，有W(u,v,x)≥3n。

综上所述，可得|NCn(u)∪NCn(v)∪NCn(x)|≥3n-2，引理2得证。

引理3 若n≥4，假设Cn中存在1个由1条故障边和多个故障顶点组成的集合S且|S|≤n，令F1和F2表示Cn中2个不同的故障顶点集合，且满足条件F1≤δ(Cn-S)和F2≤δ(Cn-S)，则当F1-F2中有顶点u,在F2-F1中有顶点v，且(u,v)∈E(Cn)时，F1和F2是1对可区分对。

证明 使用S表示Cn中由1条故障边和多个故障顶点组成的集合S且|S|≤n，即S是V(Cn)∪E(Cn)的1个子集。由定理4可知，当|S|=0时，F1和F2是1对可区分对。

因此，仅需考虑当|S|≥1时的情形。因为(u,v)∈E(Cn)，由定义1，有|NCn(u)∩NCn(v)|≤2。因为|F1|≤δ(Cn-S)和|F2|≤δ(Cn-S)，可以得到|F1|+|F2|≤2δ(Cn-S)。根据定义1和定理3，可以得到δ(Cn-S)<δ(Cn)=n+1。

假设F1和F2是1对不可区分对，则对于在F1ΔF2=(F1-F2)∪(F2-F1)中的任意顶点x，都有NCn-S(x)⊆F1∪F2。此时，将分为以下2种情形讨论：

情形1 当(u,v)∈S时，可得|F1|+|F2|≥|NCn-S(u)∪NCn-S(v)∪{u,v}|=|NCn-S(u)|+|NCn-S(v)|+|{u,v}|≥2δ(Cn-S)+2。这与条件|F1|+|F2|≤2δ(Cn-S)矛盾，故该情况不成立。如图4a所示。

情形2 当(u,v)∉S时，此时(u,v)∈E(Cn)，由定义1，有|NCn(u)∩NCn(v)|≤2。进而可以得到|NCn-S(u)∪NCn-S(v)-{u,v}|=degCn-S(u)+degCn-S(v)-2≥2n-|S|。如图4b所示。由于F1≤δ(Cn-S)，F2≤δ(Cn-S)且顶点u和v在F1ΔF2中，故可得|F1∩F2|≤δ(Cn-S)-1。进一步可以得到|NCn-S(u)∪NCn-S(v)-{u,v}|-|F1∩F2|≥2n-|S|-(δ(Cn-S)-1)≥1>0。

由此可以得出下列情形，即(NCn-S(u)∪NCn-S(v))-({u,v}∪(F1∩F2))中至少存在1个顶点x。根据先前假设，F1和F2是1对不可区分对，则对于任意顶点x∈F1ΔF2=(F1-F2)∪(F2-F1)，都满足NCn-S(x)⊆F1∪F2。根据引理2，可以得出|F1|+|F2|≥|NCn-S(u)∪NCn-S(v)∪NCn-S(x)|≥|NCn(u)∪NCn(v)∪NCn(x)|-|S|≥(3n-2)-|S|。然而这与先前条件|F1|+|F2|≤2δ(Cn-S)矛盾，因此该情况不成立。

Figure 4 Distribution of vertices u,vand their neighbors in Cn图4 Cn中顶点u和v及其邻居的分布情况

综上所述，若F1-F2中存在顶点u，在F2-F1中存在顶点v，且满足(u,v)∈E(Cn)时，F1和F2是1对可区分对。

定理5 给定Cn上存在由1条故障边和多个故障顶点组成的集合S且|S|≤n，则当n≥4时，Cn-S是δ(Cn-S)-可诊断的。

证明 假设在Cn-S中存在满足条件max{|F1|,|F2|}≤δ(Cn-S)的1对不可区分对F1和F2。由于F1和F2是一对不可区分对，则对于在F1ΔF2=(F1-F2)∪(F2-F1)上的任意顶点u，都有NCn-S(u)⊆F1∪F2。

由于F1≠F2，那么在F1-F2中至少存在1个顶点，假设该顶点为v。因为F1≤δ(Cn-S)，degCn-S(x)≥δ(Cn-S)，NCn-S(x)⊆F1∪F2，且v∈F1-F2。所以，至少存在1个顶点x分布于(NCn-S(v)∩F2)-F1中。根据引理3可知，F1和F2是1对可区分对，这与假设矛盾，由定理2可知，当n≥4时，Cn-S是δ(Cn-S)-可诊断的，故定理得证。

定理6 给定Cn上存在由1条故障边和多个故障顶点组成的集合S且|S|≤n，则当n≥4时，Cn-S的诊断度是δ(Cn-S)。

证明 根据定理5可知，当n≥4时，Cn-S是δ(Cn-S)-可诊断的。因此，仅需证明Cn-S中存在1对不同的故障顶点集合F1和F2，使得F1和F2是1对不可区分对，其中F1≤δ(Cn-S)+1且F2≤δ(Cn-S)+1。

假设Cn-S中存在顶点u满足条件degCn-S(u)=δ(Cn-S)。令F1=NCn-S(u)∪{u}且F2=NCn-S(u)，则可以验证|F1|=δ(Cn-S)+1和|F2|=δ(Cn-S)，根据定理1可知，F1和F2是1对不可区分对。

综上所述，当n≥4时，Cn-S的诊断度是δ(Cn-S)。

4 交错立方体上的故障诊断算法

定理6证明了n维交错立方体在故障情形下的诊断度。根据引理3和定理5研究思路，本节提出一种在该情形下基于PMC模型的时间复杂度为O(Nlog2N)的快速诊断算法CDiag，其中N表示Cn的顶点总数。

在算法CDiag中，分别用M和F表示1个无故障集合和故障集合，PMC(u,v)表示顶点u对顶点v的测试结果。具体算法如下所示：

算法:CDiag

输入:当n≥4时，n维交错立方体Cn上存在由1条故障边和多个故障顶点组成的集合S且|S|≤n。

输出:诊断出的故障顶点集合F。

步骤1 令F←∅,M←∅,G←Cn-S,k←δ(G)；

步骤2 令u←FindFFNode(G,k)；

步骤3 returnDiagMain(G,u,M,F,k)；

functionFindFFNode(G,δ)

步骤1 for (u,v)∈E(G) then

步骤2 ifPMC(u,v)=0andPMC(v,u)=0 then

步骤3 令k←1；

步骤4 forx∈(NG(u){v})then

步骤5 ifPMC(u,x)=0 andPMC(x,u)=0 then

步骤6 令k←k+1；

步骤7 fory∈(NG(v)u}) then

步骤8 ifPMC(v,y)=0 andPMC(y,v)=0 then

步骤9 令k←k+1；

步骤10 ifk>δthen

步骤11 returnu；

end function

functionDiagMain(G,u,M,F,δ)

步骤1 forv∈NG(u) then

步骤2 ifv∈(M∪F) then

步骤3 if |M∪F|=|V(G)|or |F|=δthen

步骤4 returnF；

步骤5 else

步骤6 ifPMC(u,v)=0 then

步骤7 令M←M∪{u,v}；

步骤8 if |M∪F|=|V(G)| or |F|=δthen

步骤9 returnF；

步骤10 else

步骤11 returnDiagMain(G,v,M,F,δ)；

步骤12 else

步骤13 令M←M∪{u}，F←F∪{v}；

步骤14 if |M∪F|=|V(G)| or |F|=δthen

步骤15 returnF；

步骤16 if |M∪F|=|V(G)| or |F|=δthen

步骤17 returnF；

end function

算法分析：当n≥4时，给定1个n维交错立方体Cn和满足一定条件的故障集合S。算法CDiag能够在Cn-S(用G表示)上诊断出δ(G)个故障顶点。算法CDiag首先调用函数FindFFNode找出1个无故障顶点u，然后调用函数DiagMain遍历网络G的顶点，通过对整个网络G的顶点进行分类，将识别出的故障顶点放入故障顶点集合F中，无故障顶点放入无故障顶点集合M中，最终精确诊断出G上的δ(G)个故障顶点，算法的流程图如图5所示。

Figure 5 Flow chart of CDiag algorithm图5 算法CDiag的流程图

举例说明：当n=4时，C4上存在由1条故障边(1111,1100)和3个故障顶点{1101,1000,0000}组成的集合S。经过算法CDiag步骤1，G是由顶点集合{0110,0111,0001,0011,0010,0101,0100,1111,1110,1100,1010,1011,1001}和边集合{(0110,1110),(0110,0111),(0110,0101),(0110,0100),(0110,0010),(0111,0101),0111,0001),(0111,0100),(0001,1011),(0001,0011),0001,0010),(0011,0101),(0011,1001),(0011,0010),(0010,1010),(0101,1111),(0101,0100),(0100,1100),(1111,1110),(1111,1001),(1110,1010),(1110,1100),(1010,1011),(1010,1001),(1011,1001)}构成的图，且k=2；经过算法CDiag步骤2，找出1个无故障顶点0110；经过算法CDiag步骤3，最终找出故障顶点集合{1101,1000,0000}。

下面分析该算法的时间复杂度。本节使用邻接表存储图G，使用N表示Cn的顶点总数，显然N=2n。根据定义1，可在O(Nlog2N)内计算出δ(G)和E(G)，在O(N)内计算出V(G)，在O(n) 内计算出NG(u)，这些值可在程序调用前预先计算出来，而算法CDiag可在常数时间内调用这些数值。另外，根据PMC模型的定义，可在常数时间内计算出PMC(u,v)。函数FindFFNode中步骤1需要O(n)，步骤2～步骤3需要O(1)，步骤4～步骤11需要O(n)。因此，函数FindFFNode的时间复杂度为O(n2)。函数DiagMain采用广度优先搜索方法诊断故障顶点，其最坏情形下，时间复杂度为O(2n+n2n)=O(Nlog2N)。综上所述，算法CDiag的时间复杂度为O(Nlog2N)。

5 模拟实验及结果分析

本节将本文设计的诊断算法CDiag与Sengupta-Dahbura提出的诊断算法FDiag(其时间复杂度为O(N5))、张丽果等[9]提出的诊断算法DDiag(其时间复杂度为O(N2))进行比较，文献[9]设计的诊断算法DDiag在故障点数量较小时具有较高的可靠性。本文对上述算法用Python语言编程实现，用1台配置为Intel Core(TM) i5-7Y54 CPU 1.20 1.61 GHz，8 GB内存的计算机来评估算法的性能，并分析实验结果。实验中边故障和顶点故障都是随机生成的。

实验1 给定1个12维的交错立方体C12(共4 096个顶点)在故障情形(由1条故障边和多个故障顶点组成的故障集合S)下，利用算法CDiag诊断出δ(C12-S)个故障顶点所花费的CPU时间。算法CDiag重复运行100次的最坏和平均情况分别如图6a和图6b所示。

Figure 6 CPU time of fault diagnosis图6 故障诊断花费的CPU时间

根据实验结果可以看出，对C12-S进行故障诊断消耗的CPU时间与其网络上顶点数量相关，与S中元素数目的关联性不大。对比使用文献[9]中算法DDiag的实验结果，平均CPU时间900～1 000 ms，最坏CPU时间为1 100～1 300 ms。对比使用文献[11]中算法FDiag的实验结果，平均CPU时间为1 100～1 200 ms，最坏CPU时间为1 300～1 500 ms。由实验数据可以看到，本文算法的执行效率优于文献[9]和文献[11]中算法的。

实验2 给定1个10维的交错立方体C10(共1 024个顶点)。利用算法CDiag基于PMC模型计算C12中诊断出k个故障顶点的成功率，其中k∈{0,50,100,150,200,250,300,350,400,450,500}。进一步，将算法CDiag重复运行100次的成功率与文献[9]中算法DDiag和文献[11]中算法FDiag的实验结果相比较，如图7所示。

根据算法CDiag的实验结果，随着数值k的不断增加，10维的交错立方体C10诊断出k个故障顶点的成功率在k≥300时逐步降低，随着故障顶点数量增加，C10上存在多个连通分支几率逐渐增大，故成功率逐步降低。对比使用文献[9]中算法DDiag的实验结果，当k≥50时成功率逐步降低,并且下降速度快于算法CDiag的。对比使用文献[11]中算法FDiag的实验结果，当k≥50时成功率逐步降低,并且下降速度与算法CDiag接近。由实验数据可以看到，本文算法的稳定性优于文献[9]中算法，并且与文献[11]中算法接近。

Figure 7 Success rate of fault diagnosis图7 故障诊断的成功率

综上所述，本文提出的诊断算法CDiag与Sengupta-Dahbura提出的诊断算法(其时间复杂度为O(N5)[11])和张丽果等提出的诊断算法 (其时间复杂度为O(N2)[9])相比，在高效性方面较优。进一步，其稳定性方面优于文献[9]中算法，并与文献[11]中算法接近。

6 结束语

诊断度和诊断算法是互连网络中可靠性研究的重要课题，而基于PMC模型的诊断方法是互连网络的一种常用的系统诊断方法。本文首先证明了基于n维交错立方体在出现故障边和故障顶点的情况下的诊断度，然后提出了该故障情形下的快速诊断算法，并基于该算法进行了相应的仿真实验。实验结果显示，在多种故障参数下本文所提算法的性能优于对比算法。近年来，研究者们对互连网络的诊断度和诊断算法做了大量的研究，并且延伸到无线传感网络、P2P网络等方向。因此，这些网络出现类似故障情形时，其系统的诊断度和诊断算法还有待于进一步的研究。