单桩基础海上风力机防护装置的船舶碰撞试验与数值对比分析

宋泽成，王 蕾，任年鑫，李炜

(1.济南大学土木建筑学院，山东 济南 250022; 2.海南大学土木建筑工程学院，海南 海口 570228;3.大连理工大学海岸及近海工程国家重点实验室，辽宁 大连 116024;4.中国电建集团华东勘测设计院，浙江 杭州 310014)

随着海上风电场如雨后春笋般在世界范围内的兴起[1]，恶劣海洋环境条件下，大型海上风力机遭受船舶意外碰撞的可能性也日益增高[2-3].海上风力机是一种典型的顶部带有集中大质量的高耸结构，其底部发生的碰撞大变形极易引起整体结构的失稳倒塌，因此，深入研究船舶碰撞海上风力机结构的动力响应特征，即有着深刻的学术意义，又有着重要的实际工程意义.

相关海上风电场的设计规范(IEC 61400-3[4]、DNV-OS-J101[5]等)均涉及了一些有关船舶碰撞海上风力机的参考建议，但由于其大都仅仅局限于简化的准静态分析方法，很难全面细致地揭示整个复杂碰撞过程的作用机理.一些学者[6-10]曾尝试利用LS-DYNA非线性有限元软件分别对船舶碰撞单桩基础、三桩基础和导管架基础的海上风力机过程进行过数值模拟，并获得了一些有实际参考价值的结论.目前，单桩基础在近海风力机基础形式中应用得最为广泛，但由于单桩基础的水平刚度相对较弱，因此在船舶遭遇意外碰撞情况下其整体结构较为危险，为此，一些学者尝试性地提出了几种适用于单桩基础海上风力机结构的防船舶碰撞装置，主要包括：球壳-泡沫铝结构[11]、充气结构[12]、橡胶隔垫结构[13]、钢板-橡胶结构[14]等，并主要基于非线性有限元方法，对其防撞性能进一步进行了较为系统的研究，揭示了其各自的动力响应特征及防撞效果.此外，任年鑫等人[15]采用1∶50缩尺物理模型试验的方法，重点研究了一种新型单桩基础海上风力机防撞装置的防护性能，并提出了优化设计建议.

目前，有关船舶碰撞海上风力机的物理模型试验的研究还非常有限，更缺少数值模拟结果与相关模型试验数据的对比验证研究.因此，本文分别基于简化缩尺物理模型试验和非线性有限元软件LS-DYNA方法，对比研究了在有/无防护装置下船舶碰撞单桩基础海上风力机的动力响应特征，以此揭示新型防护装置的防护性能及物理作用机理，并将数值模拟结果与相关物理模型试验结果进行了对比验证.

1 物理试验模型简介

本试验模型依托江苏某4 MW单桩基础海上风力机的实际工程项目，该项目由中国电建集团华东勘测设计院参与建设，相关海域水深15 m，附近配套运维船舶为2 000 t以下.相关船舶碰撞海上风力机物理模型试验在大连理工大学海岸及近海工程国家重点试验室进行，如图1所示.主要基于动力相似准则，选取1∶50缩尺比，主要模型参数如表1所示.

表1 船舶碰撞单桩海上风力机模型试验主要设计参数

鉴于目前缩尺模型试验桩-土耦合作用的精确模拟仍非常难以实现，故本文单桩风力机基础采用的是简化的底部固结连接方式，即忽略桩土相互作用.利用简化小车模型(通过不同配重铅块)模拟不同船舶质量，并利用直流电机、传动杆和配套平台轨道装置控制模拟船舶的不同碰撞速度.小车模型碰撞防护装置的细部结构如图2所示，小车前端设置有一个高精度压力传感器(精度0.001 N，采样频率1 000 Hz)，用于测量碰撞力；船舶撞击塔架部位的防护装置由外层薄壁钢板和内层橡胶隔垫结构组成.此处仅给出缩尺模型实验的简略介绍，相关物理模型试验更为详细的介绍可参考文献[15].

2 数值模型

基于广泛应用于碰撞分析的非线性有限元软件(LS-DYNA软件)，参照物理试验模型设计参数，构建了船舶碰撞单桩基础海上风力机结构的数值模型，如图3所示.为了便于数值结果与试验数据的对比分析，数值模型中的碰撞船体也采用“小车模型”，并简化为刚体结构，同时考虑了船体碰撞的附粘水效应，即10%船重[16].

考虑到风力机塔架和防护装置薄壁钢壳在碰撞过程中对材料应变率的影响，故选取非线性塑性材料模型(*MAT_PLASTIC_KINEMATIC[17])来描述钢材本构(Cowper-Symonds)，具体描述如下：

(1)

式中，σv、ε、σ0、Ep、εpeff分别表示动态极限屈服应力、应变率、初始屈服强度(345 MPa)、可调参数(0.8)、塑性强化模量(3 GPa)和等效塑性应变；C 和 P为与材料性质有关的常数.

防护装置的橡胶隔垫层材料选用Mooney-Rivlin模型(MAT_MOONEY- PIVLIN_RUBBER[17])，其应变能密度函数W是变形张量不变量I1、I2和I3的函数，即：

W=C10(I1-3)+C01(I2-3)+C(I-23-1)+D(I3-1)2，

(2)

3 模拟结果对比分析

为了便于理解，本部分的相关物理模型试验数据和数值结果都已折算为全尺度模型.

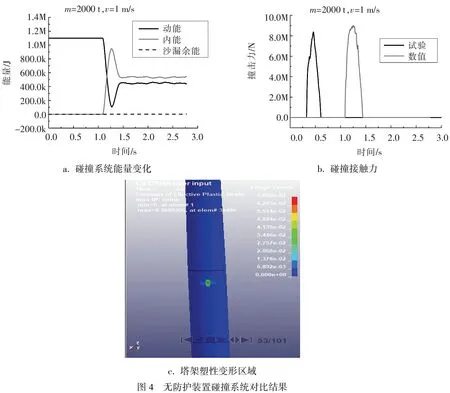
3.1 无防护装置碰撞模拟参照DNV-OS-J101[5]国际规范，选取具代表性的船舶碰撞海上风力机工况，即船舶质量2 000 t，碰撞速度1 m/s.对比分析了在无防护装置下该碰撞结构系统动力响应的主要数值和试验结果，如图4所示.

从图4a的系统能量变化时程曲线可以看出，在船舶与风力机塔架结构发生碰撞后，船舶的动能逐渐转换为风力机塔架结构的变形能.需要指出的是，此数值模拟系统的沙漏余能远小于碰撞系统总能量的1%.图4b给出了碰撞接触力的对比时程曲线，数值结果与试验结果有着很好的一致性，数值模拟结果略大于试验结果，这可能是由于物理试验模型中的下部固结基础很难做到绝对的固结及小车模型并非绝对不变形刚体等原因，即数值模型中忽略了单桩基础和小车模型的弱弹性效应，因此略高地估计了碰撞力的峰值.此外，图4c给出了受碰风力机塔架上的塑性变形区域，相关碰撞区域的结构损伤将严重威胁风力机整体结构长期服役的安全性.

3.2 有防护装置碰撞模拟为尽可能避免由船舶意外碰撞所导致的海上风力机重要主体结构的塑性变形损伤，防船舶碰撞装置对保障大型海上风力机在长期服役期中的结构安全具有一定的必要性.为此，参照本研究团队所提出的海上风力机防船舶碰撞装置[15]，进一步对比分析了该防护装置对碰撞系统结构动力响应特征的影响，主要结果如图5所示.

对比图4a中的系统能量变化时程曲线，图5a所给出的有防护装置碰撞系统的能量曲线随时间的变化相对更为平滑.从图5b所给出的碰撞接触力时程对比曲线可以看出，在有防护装置情况下，数值结果与试验结果也有着很好的一致性.如果将图5b与图4b进行对比分析，有防护装置情况下的碰撞接触时间比无防护装置的碰撞接触时间长，且碰撞力峰值显著小于无防护装置系统的碰撞力峰值，即有防护装置的最大撞击力约为无防护装置工况下最大撞击力的60%.图5c进一步给出了有/无防护装置两种工况下碰撞系统主要结构变形能的时程曲线，由图5c可以看出，在有防护装置的情况下，防护装置的外层薄壁钢板首先与船舶碰撞接触，并利用自身结构的塑性变形充分吸收船舶碰撞的能量，从而有效减弱风力机主体结构的变形能.此外，图5d给出了船舶碰撞下防护装置上的塑性变形区域，即通过防护装置(次要结构)的塑性变形有效地保护了风力机主体结构的安全.

4 结 论

本文基于简化缩尺物理模型试验和非线性有限元软件LS-DYNA相结合的方法，对比研究了船舶碰撞单桩基础海上风力机的动力响应特征，并揭示了新型防护装置对船舶碰撞接触力的影响特征及物理作用机理，获得的主要结论如下：

1)典型碰撞工况下的数值模拟结果与对应试验数据有着很好的一致性，该数值模拟方法的有效性得到了很好的验证.此外，数值模型可以更为细致地从系统能量和局部结构塑性应变等角度描述碰撞系统的动力响应特征.

2)新型薄壁钢壳-橡胶隔垫层组合结构防护装置可以有效地降低作用于风力机主体结构的最大船舶撞击力，并可利用其外层薄壁钢壳结构的塑性变形吸收船舶碰撞的能量，从而保护风力机塔架及整体结构的安全.