圆锥曲线焦点弦的一个简洁性质的证明及应用

王良彬

(浙江省杭州市仁和实验学校，310024)

圆锥曲线中焦点分弦成比例问题是一类常见问题.若焦点为弦的中点,则弦为通径,问题易解;如成其他比例关系,常规解法是由比例关系,把两交点坐标代入圆锥曲线方程,联立方程组,通过求出一交点的坐标等方法解题.由于此方法计算量较大,笔者在解题中发现,运用圆锥曲线的定义可以得到一组简洁性质，方便解题过程.

一、问题的提出

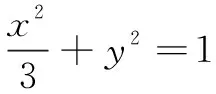
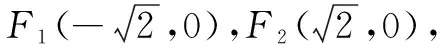
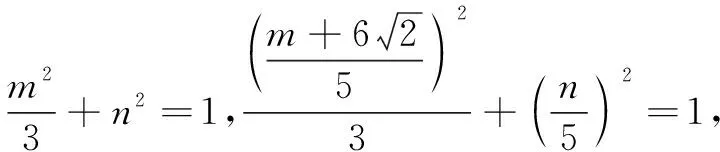
以上是此类问题的常规解法,此方法计算量较大.下面以椭圆为例，介绍笔者在解决此类问题中的一点发现.

二、解法探究

1.焦点弦的一个简洁性质

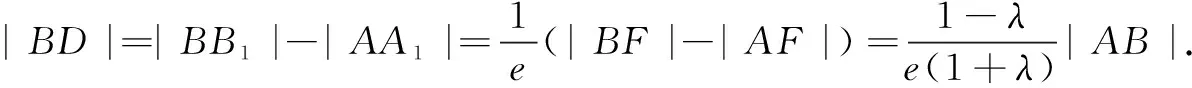
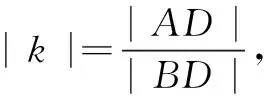
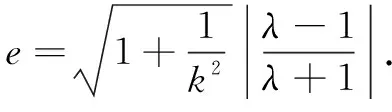
由圆锥曲线焦点弦的上述性质，可得引例的如下简洁解法.

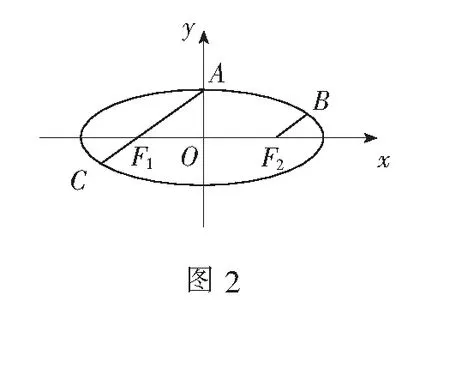
2.应用举例

例1 (2019年全国高考题)已知椭圆C的焦点为F1(-1,0)、F2(1,0),过F2的直线与C交于A、B两点.若有|AF2|=2|F2B|,|AB|=|BF1|,则C的方程为( )

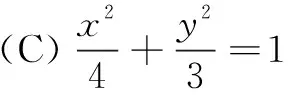
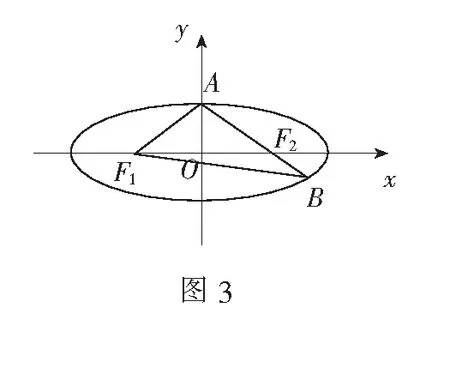
解 如图3所示,不妨设|BF2|=m,则|AF2|=2m,|BF1|=|AB|=3m.由椭圆的定义|BF1|+|BF2|=2a,得4m=2a.再由|AF1|+|AF2|=2a=4m,|AF2|=2m,得|AF1|=2m.

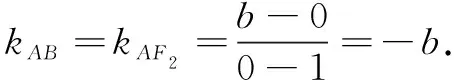
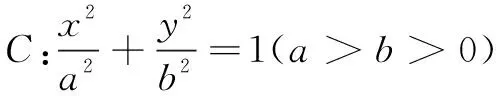
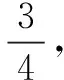
(2)若直线MN在y轴上的截距为2,且|MN|=5|F1N|,求a、b.

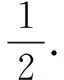
(2)由题意,原点O为F1F2的中点,MF2∥y轴,所以直线MF1与y轴的交点D(0,2)是线段MF1的中点,故点M(c,4).

b2=4a.

①

又|MN|=5|F1N|，由上述性质可得

②

直线与圆锥曲线与分线段成比例有关问题在高考中时常出现,是圆锥曲线中一类常见问题.本文是笔者在解题中的一点探究,给读者提供解决此类问题的一种方法.