点击数列与不等式的交汇题

徐加生

(江苏省金湖县教师进修学校，211600)

数列不等式是数列和不等式的交汇问题,是近年来的高考热点,这类题在很多模拟试卷中也经常见到.解决它们既要有扎实的数列和不等式的有关知识,还需要找准它们的特点及其结合点,掌握此类基本题型的解题思路,才能达到想得到、判断准、解法优的境界.本文分类探索此类交汇问题的常见题型及其解决策略，供读者参考.

一、解不等式型

有些不等式的问题中往往穿插着与数列相关的知识,通过用数列知识变形后,可化归为解不等式的问题.

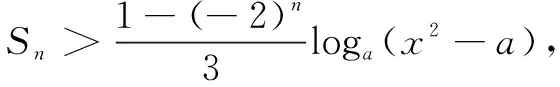
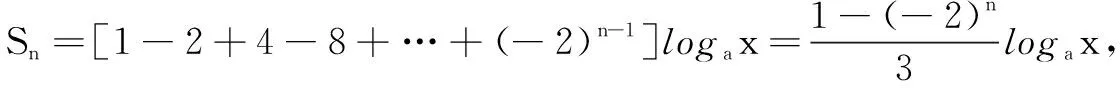
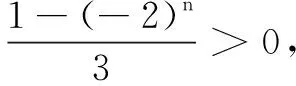
评注 本题由对数的性质简化数列通项公式是难点突破的关键.在此基础上，运用数列知识及整数的性质将不等式化简,问题归结为解一个对数不等式,其中的分类讨论必须细心,不然的话会造成错解或漏解.

二、比较大小型

与数列相关的比较大小问题,需熟悉数列求和的有关技巧及等差等比数列通项公式、前n项和公式的运用,利用已知的或已证过的不等式可大幅度简化解题过程.

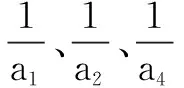
(1)求{an}的通项公式an及Sn;

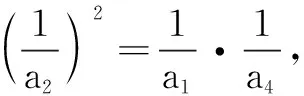
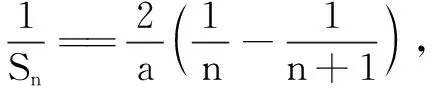
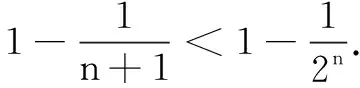
评注 本题的题型比较常见,解题的关键是如何解决求和的问题；对2n的放缩处理也是非常重要的技巧，能有效考查学生综合分析处理问题的能力.

三、不等式证明型

一些与数列或自然数相关的不等式证明题,除用数学归纳法证明外,还可用数列的有关概念、性质和不等式证明的方法来解决.

例3 设实数数列{an}的前n项和为Sn,满足Sn+1=an+1Sn(n∈N*).

(1)若a1、S2、-2a2成等比数列,求S2和a3;

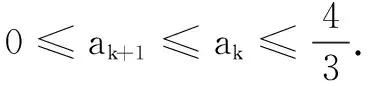
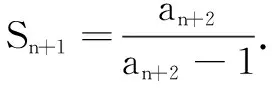
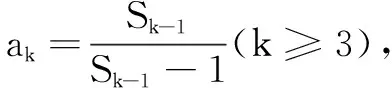
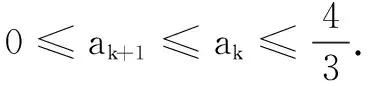
评注 本题通过深挖所给条件等式的内涵,利用等式找出了数列和式的不等关系,为比较大小创造了有利条件.而作差比较两式的大小也是重要的解题手段,必须根据解题需要及时使用.

四、求最值型

数列中的最值问题可由不等式的形式表现出来,也常与恒成立不等式相伴.解决此类问题一般是先考察数列的单调性或用比较法.

例4 在数列{an}中,a1=8,a4=2,且满足an+2-2an+1+an=0(n∈N*).

(1)求数列{an}的通项公式;

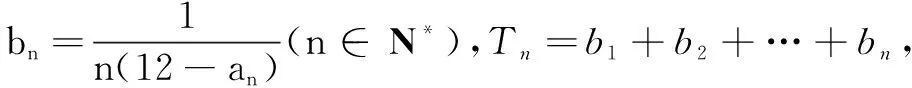
解 (1)由条件可得an+2-an+1=an+1-an,故数列{an}为等差数列.再由a1=8,a4=2,不难求得an=10-2n(n∈N*).

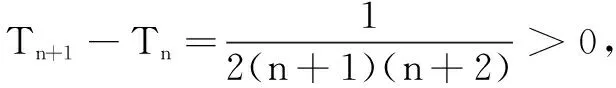
评注 对数列中求数列的最大项的问题,大多都是通过判断数列的单调情况来解决,通常只需通过求相邻两项的差来判断,这一技巧应熟练掌握.

五、求参数取值范围型

在数列不等式恒成立中,求参数范围是一种常见题型,常用解题方法是利用数列的最值列出不等式或用数列知识转化为恒不等式问题.

例5 已知数列{an}是等比数列，且首项a1>0,公比q>0,而bn=an+1-kan+2,数列{an}、{bn}的前n项和分别是Sn、Tn,如果Tn>kSn对一切自然数n都成立,求实数k的取值范围.

解 因为an+1=anq,an+2=anq2, 所以bn=an+1-kan+2=an(q-kq2),Tn=b1+b2+…+bn=(a1+a2+…+an)(q-kq2)=Sn(q-kq2).

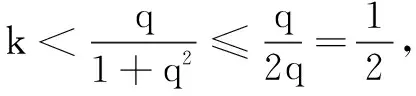
评注 解决数列中的参数问题与函数中同类问题的求解策略是一样的,比较多的是采用参数分离,再转化为求最值问题.这里需要掌握好参数分离的时机,以运算简便为佳.

六、存在性问题

此类问题是以数列不等式为载体的探索性命题,需综合利用数列和不等式知识,结合特值估算以确定参数是否存在.

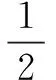
(1)用Sn表示Sn+1;

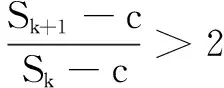
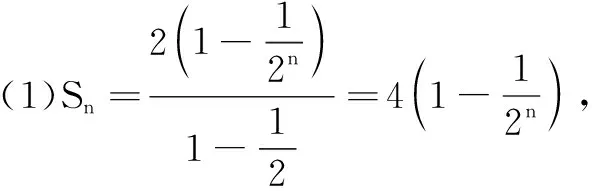
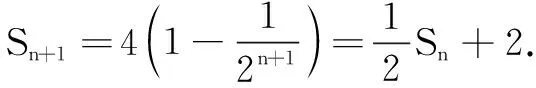
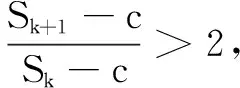
①

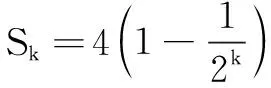
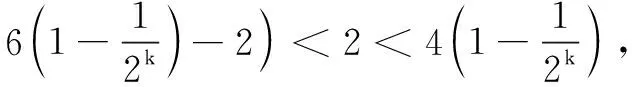
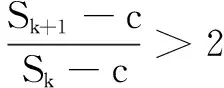
评注 存在性问题的证明过程就是数列运算化简及不等式是否成立的推理分析的过程,需要有丰富的知识储备和熟练的解题技巧,这些都需要在题目训练中不断加强.