“类周期数列”求和技巧赏析
2020-05-03叶土生
叶土生
(广东省广州外国语学校,511455)
数列求和是数列考查的热点问题,而周期数列求和是数列求和中较常见的一类问题,根据周期性求数列和一般都比较容易.对于一些与周期数列结合的非周期数列求和问题又如何解决?我们不妨称其为“类周期数列求和”问题.本文通过类比于周期数列求和介绍“类周期数列”求和的方法技巧,希望对大家有所帮助.
一、周期数列的求和
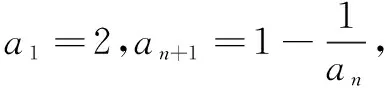
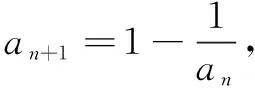
下面求前30项和S30.
解法1 (并项求和)
解法2 (分组求和 )
所以S30=S1+S2+S3=15.
评注 周期数列的求和一般可以从并项求和或分组求和两种思路出发.并项求和步骤是先每个周期进行求和,将求和问题转化为多个周期和的问题,然后再进行整体求和;分组求和就是先将相等的项组合在一起求和然后整体求和.
二、类周期数列求和
类型1 通项公式为an=(-1)nbn类型求和,其中{bn}是一般数列
例2 已知数列{an}的通项公式为an=(-1)n(2n-1),求数列{an}的前n项和.
分析 显然数列是以2为周期的数列,不妨称数列{an}为类周期数列.
解法1 (并项求和)
将同一周期的两项求和,得a2k-1+a2k=-(4k-3)+4k-1=2(k∈N*.
所以,S2m=2m,S2m-1=S2m-a2m=2m-4m+1=-2m+1.
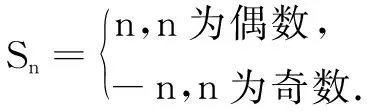
解法2 (分组求和)
按{(-1)n}的周期为2,对{an}每隔2项取出项数分组求和.
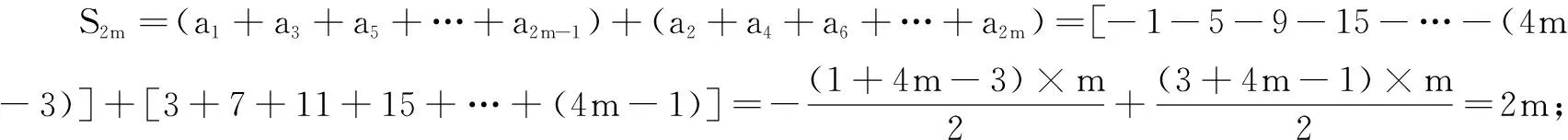
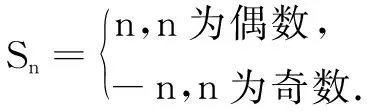
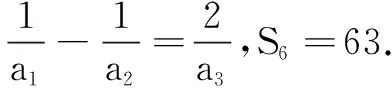
(1)求{an}的通项公式;
(2)若对任意的n∈N*,bn是log2an和log2an+1的等差中项,求数列{(-1)nb2n}的前2n项和.
解 (1)an=2n-1.(过程略)
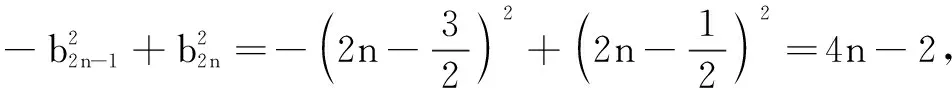
类型2 通项公式为an=bnf(n)类型求和,其中{bn}是以T为周期的周期数列
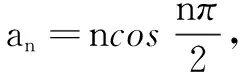
(A)1 006 (B)2 012 (C)503 (D)0
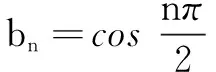
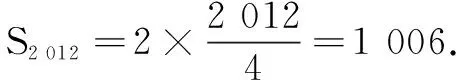
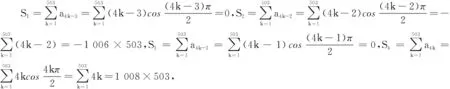
S2012=S1+S2+S3+S4=2×503=1 006.
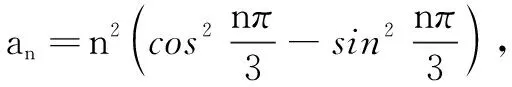
分析 先化简通项,发现{an}是以3为周期的类周期数列,再用并项或分组求和.
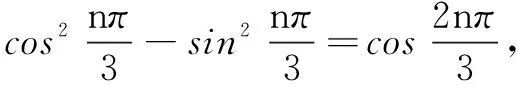
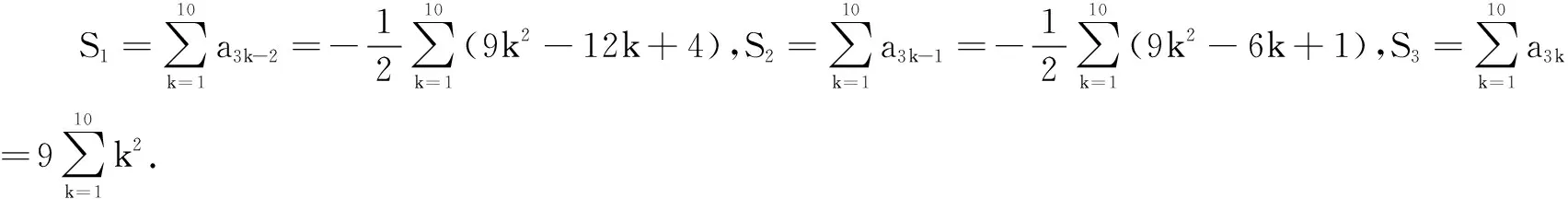
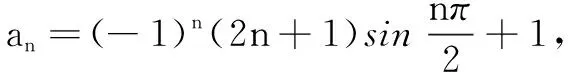
分析 此数列是类型1、2的结合体,可以先分组再并项求和.
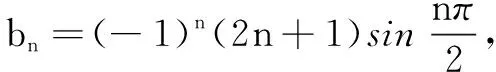
所以,S100=T1+T2+100=200.
评注 变式3的求解是采取降维的思想,先分组求和,消除其中一种周期的影响,再并项转化为常见数列的求和问题.
类型3 通项公式满足an+T-an=f(n)类型,其中T∈N*
例4 已知Sn是数列{an}的前n和,a1=1,a2=2,a3=3,数列{an+an+1+an+2}是公差为2的等差数列,则S25=______.
解 令bn=an+an+1+an+2,则有bn+1-bn=2,即an+3-an=2.所以,数列{a3k-2}、{a3k-1}、{a3k}分别是公差为2的等差数列.
解法1 (分组求和)
所以,S25=S1+S2+S3=233.
解法2 (并项求和)
由a3n-2=1+2(n-1)=2n-1,a3n-1=2+2(n-1)=2n,a3n=3+2(n-1)=2n+1,得a3n-2+a3n-1+a3n=6n.
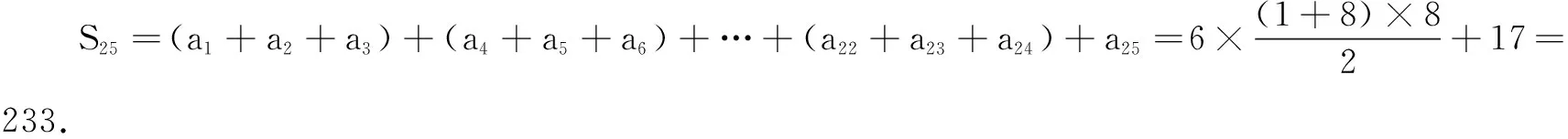
例5 (2012年全国高考题)数列{an}满足an+1+(-1)nan=2n-1,则{an}的前60项和为( )
(A)3 690 (B)3 660
(C)1 845 (D)1 830
分析 因为数列bn=(-1)n是以2为周期的周期数列,但不满足an+2-an=f(n)的形式,所以直接并项不能解决问题,但可以先按奇、偶项分成两组,然后再求和.
解法1 当n=2k时,a2k+1+a2k=4k-1;当n=2k-1时,a2k-a2k-1=4k-3.
两式相减,得a2k+1+a2k-1=2.所以a2k+3+a2k+1=2,可得a2k-1=a2k+3.
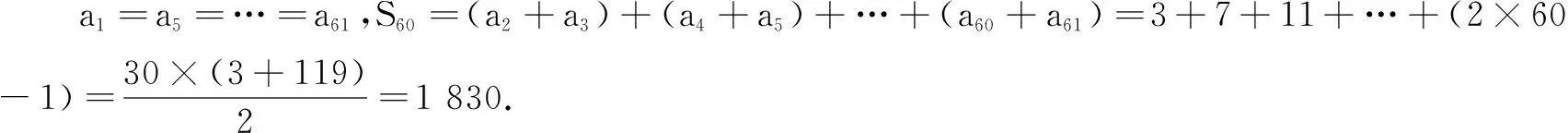
解法2 依题意,对任意k∈N*,有
a2k-a2k-1=4k-3,
①
a2k+1+a2k=4k-1,
②
a2k+2-a2k+1=4k+1.
③
②-①,得a2k+1+a2k-1=2;②+③,得a2k+a2k+2=8k.于是
S1=(a1+a3)+(a5+a7)+…+(a57+a59)=2×15=30;
所以S60=S1+S2=1 830.
三、总结提升
类比周期函数an+T-an=0,当数列递推公式经过运算满足an+T-an=f(n)形式时,我们都可以称数列{an}为“类周期数列”.通过以上的例子,说明类周期数列求和的一般策略是将其转化为一个新数列的求和问题.其方法是将连续的一个周期内的项进行并项求和构造易于求和的新数列,或先按周期T将分成T组,先求出,再整体求和.
数列求和是高考中的难点也是热点, 类周期数列这个概念尽管在目前的高中教材中没有定义过,但与类周期数列有关的问题却在高考和模拟试题中屡见不鲜.在平时的学习、教学中,要善于类比、总结,记住一些常见问题的解题方法和步骤,灵活运用方法技巧,可以起到触类旁通、化繁为简的效果,在复习备考中值得我们重视和研究.
