分类例说立体几何中的最值问题

王小莉

(山东省淄博第六中学，255000)

在立体几何中，涉及最值的问题主要有三类：一是距离(长度)的最值问题;二是面(体)积的最值问题;三是在最值已知的条件下,确定参数(其它几何量)的值.下面举例说明.

一、求体积的最值

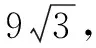
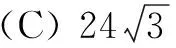
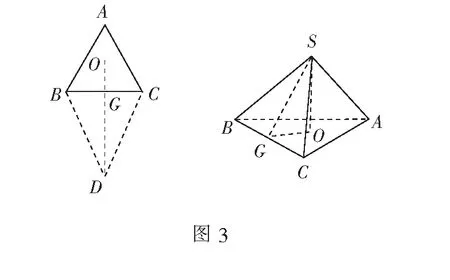
解 如图1,设点M为正三角形ABC的重心,E为AC中点,固定∆ABC，视点D为动点，易见当DM⊥平面ABC时,点D到面ABC距离最大，从而三棱锥D-ABC体积最大, 此时,相应OD=OB=R=4.

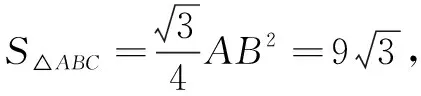
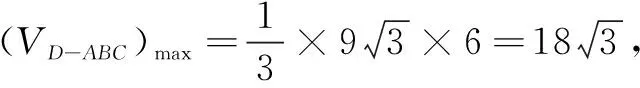
选B.

评注 在球面上利用动静相结合，判断出当DM⊥平面ABC时,三棱锥D-ABC体积最大是本题求解的关键．

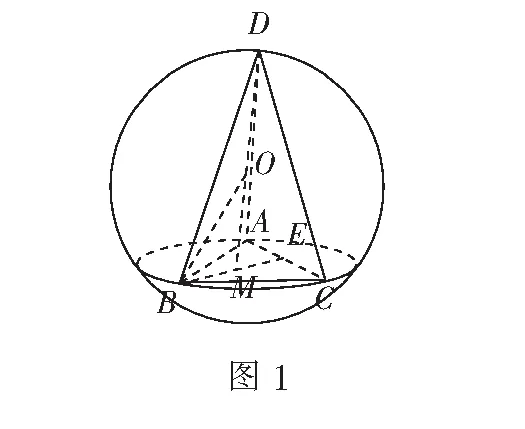
例2 (2017年全国高考题)如图2,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,∆DBC、∆ECA、∆FAB分别是以BC、CA、AB为底边的等腰三角形.沿虚线剪开后,分别以BC、CA、AB为折痕将∆DBC、∆ECA、∆FAB折起,使得D、E、F重合,得到三棱锥.当ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为______.

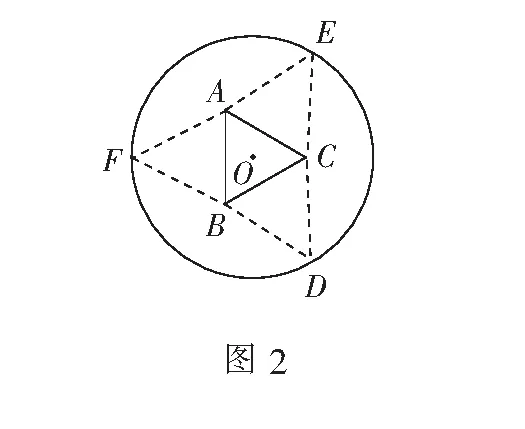
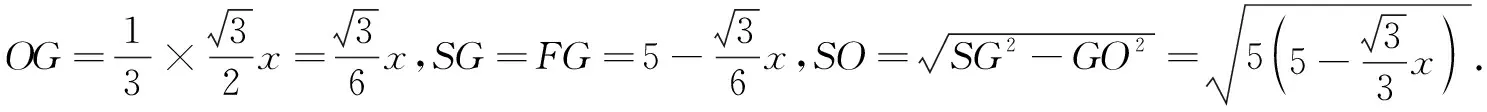
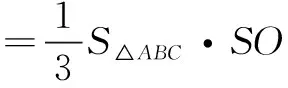
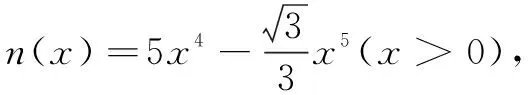
评注 对翻折问题，需分清定量与变量.本题解决的关键是设好未知量,将三棱锥的体积表示为x的函数，再利用导数法处理函数最值，使问题获解.

二、面积的最值

例3 (2018年全国高考题)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积S的最大值为( )

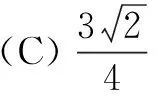
分析 由于平行线与同一平面所成的角是相等的,只要在正方体中选取从同一顶点出发的三条棱为代表来处理问题.

解 在正方体ABCD-A1B1C1D1中,平面AB1D1与线AA1、A1B1、A1D1所成的角是相等的,所以平面AB1D1与正方体的每条棱所在的直线所成角都是相等.

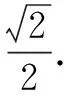
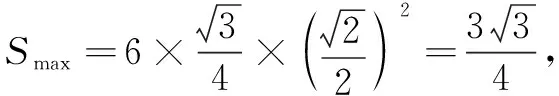
评注 本题求解的关键是将正方体的十二条棱分成三组相互平行线，由此结合正方体的对称性确定截面的位置，对空间想象力与推理能力提高了较高要求.

三、求角的最值

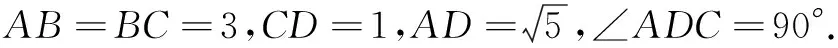
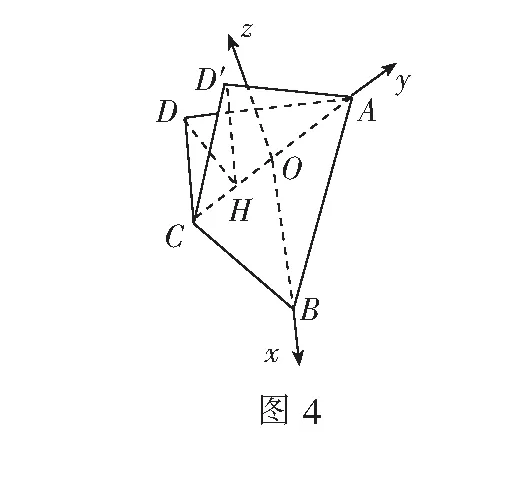
解 设O是AC的中点,如图4,以OB为x轴,OA为y轴,过O与平面ABC垂直的直线为z轴建立空间直角坐标系.由条件得

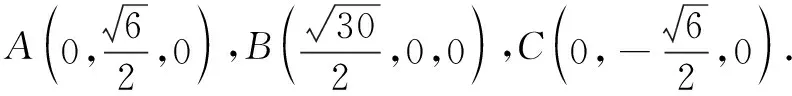
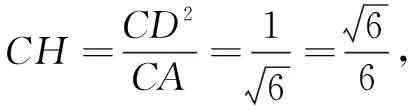
设直线AC与BD′所成角为θ，则

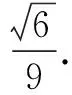
四、求与线段长有关的最值

例5 (2018年全国高考题)某圆柱的高为2,底面周长为16,其三视图如图5.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为( )

(C) 3 (D) 2

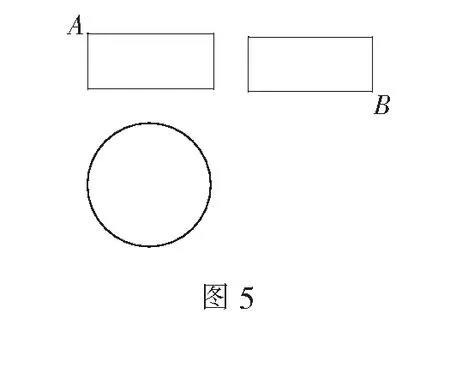
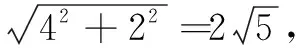
评注 该题考查的是几何体的表面上两点之间的最短距离问题.解题时需要明确两个点在几何体上所处的位置；处理方法是将面切开平铺,利用平面上两点间直线段最短进行求解.

例6 (2015年福建高考题)如图6,AB是圆O的直径,点C是圆O上异于A、B的点,ΡΟ垂直于圆Ο所在的平面,且ΡΟ=ΟΒ=1.

(1)若D为线段AC的中点,求证ΑC⊥平面ΡDΟ;

(2)求三棱锥P-ABC体积的最大值;

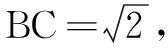
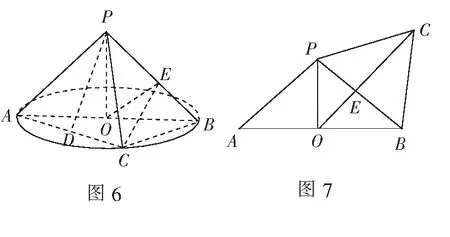
解 (1)略.

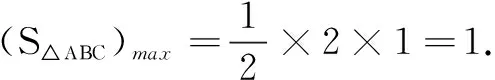
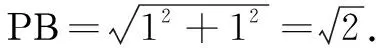
在三棱锥Ρ-ΑΒC中,将侧面ΒCΡ绕ΡΒ旋转至平面ΒC′Ρ,使之与平面ΑΒΡ共面,如图7所示.则当Ο、Ε、C′共线时,CΕ+ΟΕ取得最小值.

评注 第(3)问的求解是转化思想的重要体现.通过旋转到一个平面内,将空问题转化为平面问题，利用两点之间距离最短使问题得以解决.

五、在最值已知的条件下,确定参数(其它几何量)的值

(1)证明:平面AMD⊥平面BMC;

(2)当三棱锥M——ABC体积最大时,求面MAB与面MCD所成二面角的正弦值.

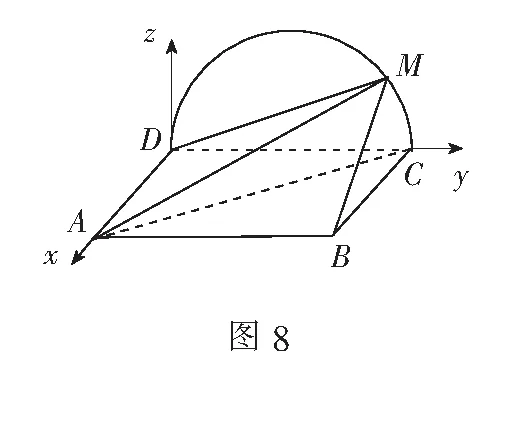
解 (1)略.

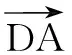
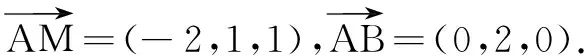
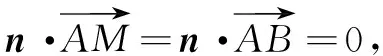
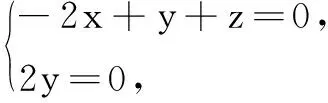
可取n=(1,0,2).