基于改进的线性调频Z变换的高精度地震波速干涉测量*
2020-05-01杨润海谭俊卿姜金钟
杨润海,谭俊卿,向 涯,姜金钟,王 彬
(1.云南省地震局,云南 昆明 650224;2.云南大学,云南 昆明 650091;3.中国地震局地震研究所 中国地震局地震大地测量重点实验室,湖北 武汉 430071)
0 引言
地震波是照亮地球内部的一盏明灯,随着地震观测和数字信号处理技术的发展,地震波不仅可以提供地球内部的结构信息,其波速变化还能反映地球内部的介质变化信息(陈颙,朱日祥,2005;陈颙等,2007a,b;丘学林等,2007;Chenetal,2008,2010)。而其中,基于背景噪声格林函数的波速变化和基于精确定位的相似地震研究是了解介质性质变化的重要方法之一(王伟涛,王宝善,2011;Xu,Song,2009)。
为了通过地震波了解地壳介质性质变化,在云南、甘肃省和新疆地区建立了大型陆地水体气枪震源观测基地(陈颙等,2017;王伟涛等,2017),并积累了多年的观测数据。如何精确测量地震波速变化就成为了解地壳介质性质变化及其过程的关键问题之一(王彬等,2012;王宝善等,2011,2016;Chenetal,2014;Liuetal,2019;Suetal,2019;Wang,Chen,2019)。
地震波速变化测量本质上是要解决数字信号处理的时延估计问题,关键是要提高时延估计的精度(刘自凤等,2015;叶泵等,2017;栾奕等,2016;向涯等,2017;林建民等,2010;Knapp,Carter,2003)。对于确定性的周期或非周期信号、或平稳随机噪声,增加取样长度有利于提高时延估计的精度;但是对于非平稳随机信号,增加取样长度将带来新的误差。尽管大容量气枪震源具有较高的重复性,而实际地震记录信号由于存在随机干扰和能量衰减,具有一定的非平稳性。同时气枪震源能量有限,传播距离较远时信号信噪比低,而传播距离较近的台站震相波列发育较短,有效信号较短,这些因素决定了进行相关计算时只能进行较短取样(蒋生淼等,2017;李孝宾等,2016,2017;徐逸鹤等,2016)。
鉴于互相关的时延检测方法受相关窗口长度和信号信噪比影响较大,本文将改进的线性调频Z变换(Modified Chirp Z Transform,简称MCZT)谱细化和相关峰精确插值(Fine Interpolation of Correlation Peak,简称FICP)引入到陆地大容量气枪主动源观测中的波速干涉测量中,介绍了一种能够获得高精度走时差的短时窗时延估计方法。
1 气枪源地震波速干涉测量方法
陆地大型水体大容量气枪的能量释放由压力脉冲和气泡脉冲组成,震源持续时间约为2 s,不是典型的脉冲源,同时存在水位和水深等影响因素。为了消除或减弱这些影响因素,通常对接收台站记录与源附近的台站(参考台)记录做反褶积运算(王宝善等,2012;翟秋实等,2016;陈佳等,2017),得到接收台近似于脉冲震源的记录,即格林函数。
目前陆地大型水体大容量气枪的波速测量,多数采用处理流程和方法如下(王宝善等,2012;Wangetal,2019):
(1)参考格林函数选取:将接收台站的格林函数叠加得到参考格林函数或者选取某一次激发的台站格林函数作为参考函数。
(2)当前格林函数选取:将每一次激发的格林函数或者相邻几次激发的格林函数叠加形成信噪比更高的格林函数,作为该段时间(内)的格林函数。
(3)震相选取:根据震源距和传播特征选取具有明确物理意义的震相,用于干涉测量,通常选取P波和S波震相。
(4)干涉测量:将当前格林函数与参考格林函数的震相信号做互相关进行时延估计,得到时延量(即走时差),然后将走时差换算成波速变化率。也可用伸缩法(行鸿彦,唐娟,2008)直接得到波速变化率。
(5)波速变化率:根据震相走时将走时差转换为波速变化率。
地震波速变化测量常用方法有互相关法、伸缩法和尾波干涉法(王宝善等,2016;Alexandre,2014)。这些方法都是基于互相关运算,相关运算可以在时域或频域进行,本文主要讨论在频域计算中如何提高计算精度。而在频域进行互相关计算时,需要较精确的频谱估计。
标准快速傅里叶变换(Fast Fourier Transform,简称FFT)的计算速度快,但对于实数序列的FFT计算存在2个显著的缺陷:一是在计算结果中,序列左半边代表信号的频谱,右半边是左半边的共扼对称,只有一半是有用信息,浪费了另一半;二是FFT计算出的信号的频谱相当于对频谱的离散抽样,存在栅栏效应。谱分辨率受取样长度tp制约,Δf=1/tp。在满足信号平稳性的前提下,为了减小栅栏效应的影响,可以增加取样长度,但这也增加了计算量。另外,标准FFT计算的相关函数,是从N点序列到N点序列的计算,相关函数序列的点的时间间隔与采样周期一致,会降低相关波形的分辨率(间隔增加),难以得到精确的时延。针对此问题,传统的方法是对相关峰进行插值计算找峰值点,因插值结果不能完全反映相关峰的形状,因此,插值计算会带来新的误差,且增加了运算量(杨亦春等,2002)。综上认为,精确的互谱估计和互谱插值对时延的精确估计很重要。
在大容量气枪源观测中,地震仪的采样率一般为100 Hz,实际时延量远小于一个采样间隔,互相关得到的时延量只有一个采样间隔的分辨率。为了提高分辨率,对互相关函数的相关峰通过余弦插值等方法进行插值,可以得到更精确的时延估计值,取得较好的结果(Wangetal,2019)。但余弦插值计算过程与信号的信息无关,即与互谱无关,插值结果只能近似反映相关峰的形状。因此要达到计算精度更高而计算量小的目的,有必要寻求同时提高互谱和相关峰计算精度的方法。为此,本文探讨利用MCZT谱细化和FCIP在陆地大容量气枪主动源观测中的波速干涉测量的应用,并与余弦插值方法进行了对比。
2 MCZT谱细化
频谱的细化计算常见的方法有ZOOM算法、频率抽取法、降采样法、ZFFT(降采样)、cFFT(级联FF)等(杨亦春等,2002;侯朝焕等,1990),这几种方法的共同特点是计算量大。MCZT算法可在不增加计算量的前提下提高频谱计算精度(马少春等,2014;杨亦春等,2003;唐娟,行鸿彦,2007;杜娟,程擂,2010;王莉等,2011;徐世友,2003;Benestyetal,2004)。
对长度为N的时域序列x1(n)和x2(n),其相关函数为:
R(m)=E[x1(n)·x2(n+m)]
(1)
式中:R表示相关函数;m表示时延;E表示数学期望;n表示时间。
相关函数的主峰对应的时间就是信号x1(n)和x2(n)之间的时延量,R(n)的频谱R(k)与x1(n)和x2(n)的频谱X1(k)和X2(k)的关系为:
R(k)=X1(k)·X*2(k)
(2)
故频谱计算精度直接影响相关函数的精度。
MCZT定义为:
(k= 0,1,…,N-1)
(3)
定义MCZT的逆变换为IMCZT:
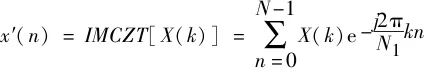
(4)
由式(3)(4)可看出,x′(n)不等于x(n),IMCZT与MCZT的计算结果在数值上是共轭关系,MCZT是CZT(线性调频Z变换)的一个特例。频谱的间隔由N1决定,Δf=fs/N,fs为信号采样率,当N1=fs时,频谱的分辨率就达到1 Hz,N1的选择不受N的限制,可以采用FFT实现快速计算。采用MCZT计算出的信号频谱,是从0 Hz开始到fmax=fs*(N/N1)Hz,即是截取了一段低频谱,为保证不影响相关精度,应该覆盖信号的主要频率范围(Sorensen,Burrus,1993),该方法适用于对低频信号分析。
主动源台阵接收到的主要信号频率为2~7 Hz,相对于100 Hz的采样率,MCZT不仅能计算出了被FFT丢失的谱,而且谱峰的高度也更加精确。另外由于MCZT只计算了有用信息所在的频段,因此还具有抑制宽带噪声的作用。
3 FICP算法
FICP最基本的思想是对2个信号的互谱补零,从而提高相关函数的分辨率。从采样定理可知,采样信号的频谱相当于原始信号频谱的周期重复,且重复间隔等于采样频率。离散傅里叶变换(Discrete Fourier Transfrom,简称DFT)计算出的信号频谱,其右半部分是左半部分的共扼对称,总长度对应采样率数值。提高采样率并增加序列点数(tp不增加)不会改变频谱的形态,只会拉开左右两段谱之间的间隔。因此,如果把计算出的频谱中间加零,拉开左右距离,逆变换计算出的时域波形的采样率就会提高(侯朝焕等,1990)。
对于2个信号x1(n),x2(n)(n=0,1,…,N-1),加窗函数W(n)(n=0,1,…,N-1)后,用MCZT分别计算其细化频谱,根据相关定理计算得到2个信号的互谱:
R(k)=X1(k)·X2(k) (k=0,1,…,N-1)
(5a)
式中,R(k)只是谱的前一部分,通过谱的共轭对称性,对R1(x)补零扩展为N1点R(k):
(5b)
通常信号的时延处在有限范围内,相关函数的主峰处在零值附近,因此只需要计算相关波形的左边(后段)有限点和右边(前段)有限点。实现这一算法的方法可以采用有限点时域(或频域)序列计算在有限点频域序列(或时域)的算法(Sorensen,Burrus,1993)该方法虽然考虑到了减少计算量的问题,但是不能对变换结果进行插值运算。在计算时延时,只需要计算相关峰附近的点,为此可以对逆变换计算进行简化。
按照式(5b)将互谱拉开,设定互谱的长度为N2, 对于n=0,1,…,N-1的时域范围,相关函数前段为:
(6)
将式(6)两项分别计算可以发现,这两项分别为IMCZT计算过程:
(7)
式中:
(8)
B(n)=IMCZT[R3(k)]
(9)
式中:
(10)
同理,对于n=N2-N,N2-N+1,…,N2-1的时域范围, 取n=N2-N+n1, 对应的n1=0,1,…,N-1相关函数为:

(11)
式中:
(n=N2-N+n1;n1=0,1,…,N-1;k=0,1; …,N-1)
(12)
式中:
(13)
F(n)=G(n)·IMCZT[M(k)]
(14)
(15)
(16)
由此可组合出相关波的峰为:
智慧交通公共数据与服务支撑平台,违章违停数据已有30多万条,公交车位置数据有3206万条,虚拟卡口过车数据约有1.6亿条,路边停车次数有50多万次。随着各项数据的积累,未来的吉首将运用大数据分析平台提升吉首市的现代化水平,建立健全的大数据辅助科学决策和社会治理机制,推进政府管理和社会治理模式的创新,实现政府决策科学化、社会治理精准化和公共服务高效化。
(17)
通过设置N2,可以使相关函数的峰值分辨率提高N2/N1倍。
一方面,提高互谱的频谱分辨率可以使相关波形更光滑,相关峰顶更圆,且频谱的细化不受取样长度的影响;另一方面,提高插值的倍数,可以使相关峰顶分辨率提高。可见采用FICP算法可以提高时延估计的精度,特别是对于低采样的信号,其优点更明显。
4 计算分析
4.1 MCZT谱细化的计算
为考察MCZT和FFT在较短取样长度下谱的细化表达能力,将宾川气枪源的气泡振荡频率在2~7 Hz叠加合成一个仿真信号,由相对振幅分别为0.2,0.4,0.6,0.3,频率分别为2.2,3.1,4.4,5.4 Hz,采样率为100 Hz的4个正弦函数叠加而成,时长为4 s(图1)。
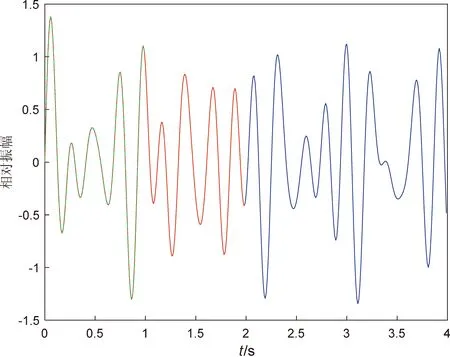
图1 仿真信号Fig.1 The simulated signals
取1 s长度(图1中绿色部分)和2 s长度分别做FFT和MCZT,得到的振幅谱如图2所示。从图2可以看出,在100 Hz采样率,1 s取样长度下,虽然有一定的误差,但MCZT能分辨出4个频率成份,FFT只能分辨出2个频率成份;在2 s取样长度,MCZT和FFT都能分辨出4个频率成份,但FFT的频率分辨率明显比MCZT的低,误差比MCZT大。
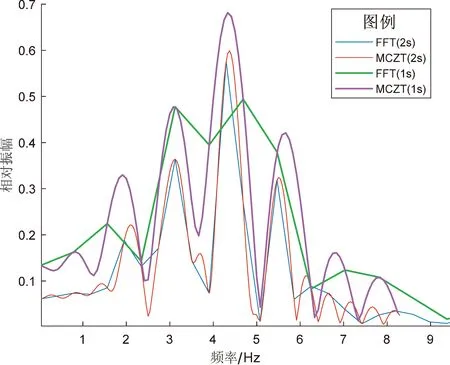
图2 仿真信号不同长度信号的MCZT细化振幅谱和FFT振幅谱Fig.2 MCZT amplitude spectrum and FFT amplitude spectrum of simulated signals with different lengths
4.2 基于MCZT和FICP的时延估计
为了评价基于MCZT和FICP的时延估计方法,先用模拟信号进行仿真实验,仿真信号由距气枪源5.5 km的乌稍台(台站代码53272)的5 000枪记录的格林函数叠加而成参考格林函数(图3a),走时在1~2 s之间的震相为P波震相,3~4 s之间的震相为S波震相。
根据伸缩法原理利用样条函数进行插值,产生1 000个具有时延在±0.5个采样间隔之间3个周期正弦变化时延(图3b)的气枪模拟记录(图3c),所有仿真记录都将最大振幅归一化为1。
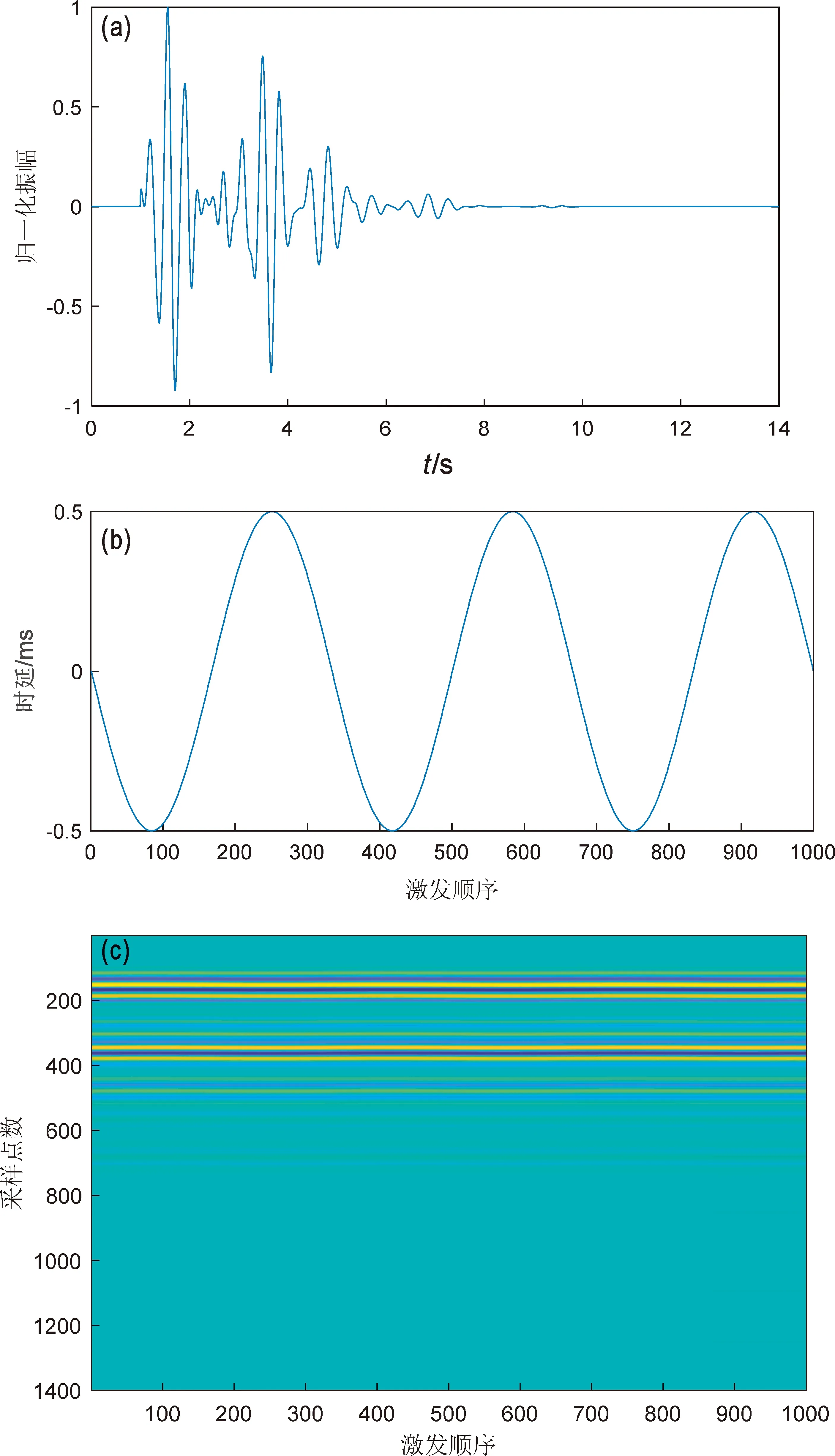
图3 参考格林函数(a)、时延变化(b)和具有时延变化的仿真信号(c)Fig.3 Reference Green function(a),time delay change(b),and simulated signals with time delay variation(c)
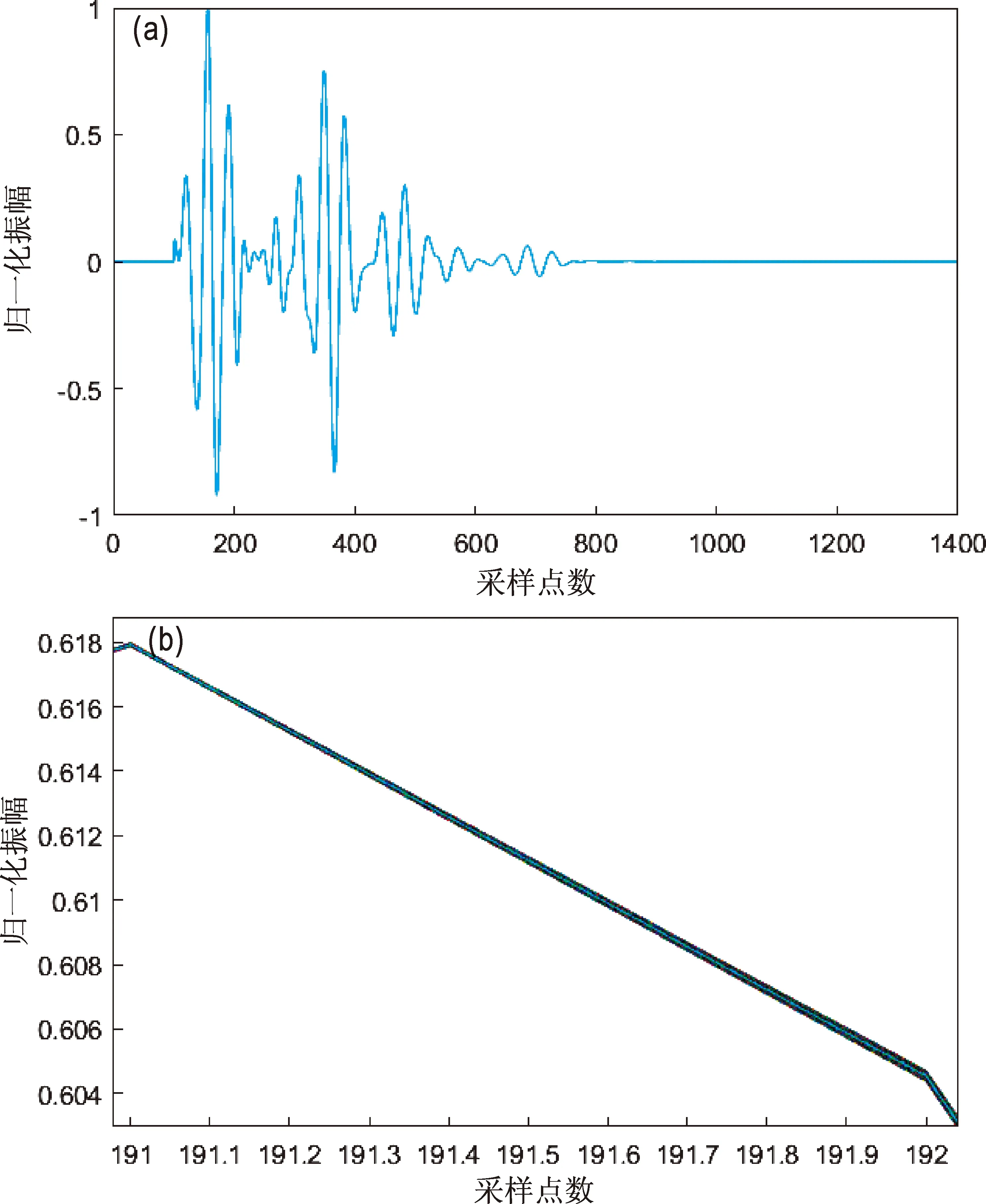
图4 1 000道仿真信号(a)及其在191~192采样点间的放大图(b)Fig.4 Simulated signals at track 1 000(a)and it’s amplification between sampling sites of 191~192(b)
从图4可以看出,最大变化量为5‰的速度变化,这在波形变化上是很细微的,不足一个采样间隔,仿真信号仅有振幅上的微小差异,延时计算需要精细的谱估计。
Srec=max[xcorr(Dr,Dt)]/norm(Dt-Dr)
(18)
式中:xcorr(Dr,Dt)表示互相关;norm(Dt-Dr)表示残差的绝对值。波速变化的恢复度值越大,波速变化的恢复效果越好。
对模拟信号添加高斯白噪声,信噪比为-20~40 dB,得到不同信噪比下的仿真信号,当信噪比≤5 dB时,使用曲波变换去噪。计算波速变化率时,参考格林函数为所有当前格林函数的线性叠加,分别对每一条当前格林函数进行计算,格林函数震相采用P波震相,信号长度约0.8 s共80个采样点,得到波速变化率(图5)。
图6为信噪比10 dB时3种方法计算得到的波速变化率,图7为计算与理论波速变化率的相关系数、残差和波速变化恢复精度。从这2个图可知,伸缩法(Stretch)、余弦插值法(CosInter)和本文方法(MCZT)都能较好地恢复波速变化率的形态,但伸缩法与理论波速变化率(Theory)残差大,余弦插值法居中,余弦插值法和本文方法无论在形态或者量值上都较好地恢复了波速的变化率,但本文方法要优于余弦插值法。

图5 信噪比10 dB时的第1和84道格林函数Fig.5 Green functions at track 1 and 84 when the signal to noise ratio is 10db
数值模拟表明,本文方法相比余弦插值法较好地克服了信号窗较短谱估计精度低的问题,因此提高了互相关估计走时差的精度。

图6 信噪比10 dB时不同方法计算得到的波速变化率与理论波速变化率Fig.6 The wave velocity change rate of different methods and the theoretical wave velocity change rate when signal to noise ratio is 10db
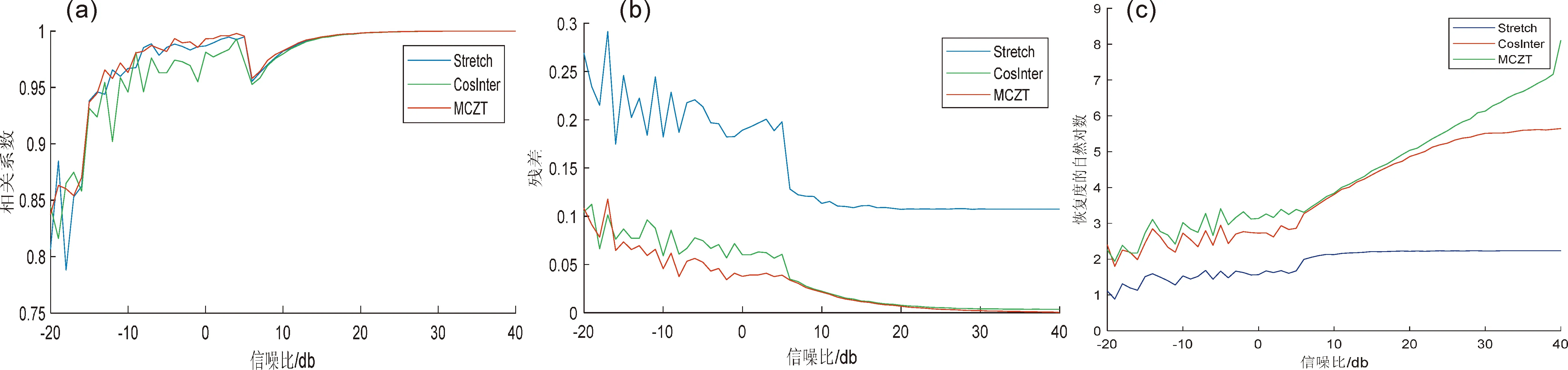
图7 在不同信噪比下测得的相关系数(a)、残差(b)和波速变化恢复精度(c)Fig.7 The correlation coefficient(a),residual(b) and recovery accuracy(c) of evaluation parameters measured under different signal to noise ratio of three methods
4.3 恢复度与窗长的关系比较
分别计算伸缩法、余弦插值法和本文方法在同一信噪比下波速变化的恢复度与时窗长度的关系,如图8所示。
在无噪声情况下(图8a),0.8~1.5 s对应的窗长范围内,波速变化率恢复度的自然对数为:伸缩法最低,本文方法最高,余弦插值法略低于本文方法。本文方法在窗长大于1 s后,恢复度基本维持水平状态,余弦插值法和伸缩法随窗长的增加,恢复度会呈缓慢增长。综合对比可知,本文方法可以在较短的窗长下获得更高恢复度及更高精度的波速变化率。从30 dB噪声情况下计算的恢复度与窗长关系(图8b)来看,同样是伸缩法最低,本文方法和余弦插值法较高,且本文方法优于余弦插值法。在有噪声情况下,波速的恢复程度与无噪声情况具有相似的特征,随着窗长增加,恢复程度都缓慢升高。在计算窗长范围时,本文方法始终优于余弦插值法、明显高于伸缩法,说明了本文方法在短时窗互相关时延估计中的优势。
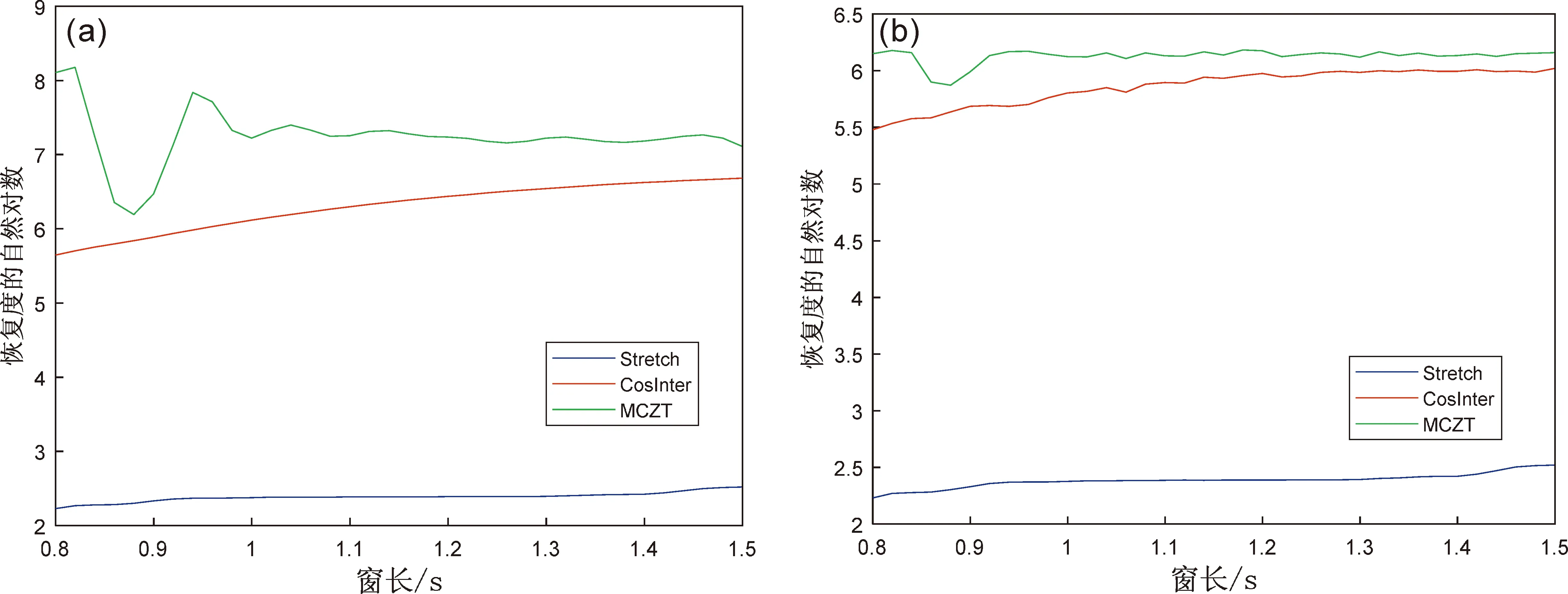
图8 无噪声(a)和信噪比为30 db(b)情况下恢复度的自然对数与窗长的关系Fig.8 Recovery degree and window length of no noise(a)and the signal to noise ratio is 30 db(b)
4.4 实际气枪记录计算
选取源检距50 km的53284台,共8 181条接收记录。因源检距较大,信号信噪比低,经相位加权叠加和曲波变换去噪后,得到8 181条去噪记录,分别用3种方法对11.0~11.30 s时窗信号进行波速变化率计算,结果如图9所示。从图中看到,在信噪比对信噪较高的记录,3种方法计算结果变化形态基本一致,伸缩法得到的波速变化率范围大于余弦插值法,本文方法得到的波速变化率范围较小。伸缩法和余弦插值法对信噪比过低的记录所得到计算结果误差较大,明显超出合理范围,而本文方法得到的波速变化率相对连续、跳跃不大、抗噪性更好,所计算的波速变化更稳定。
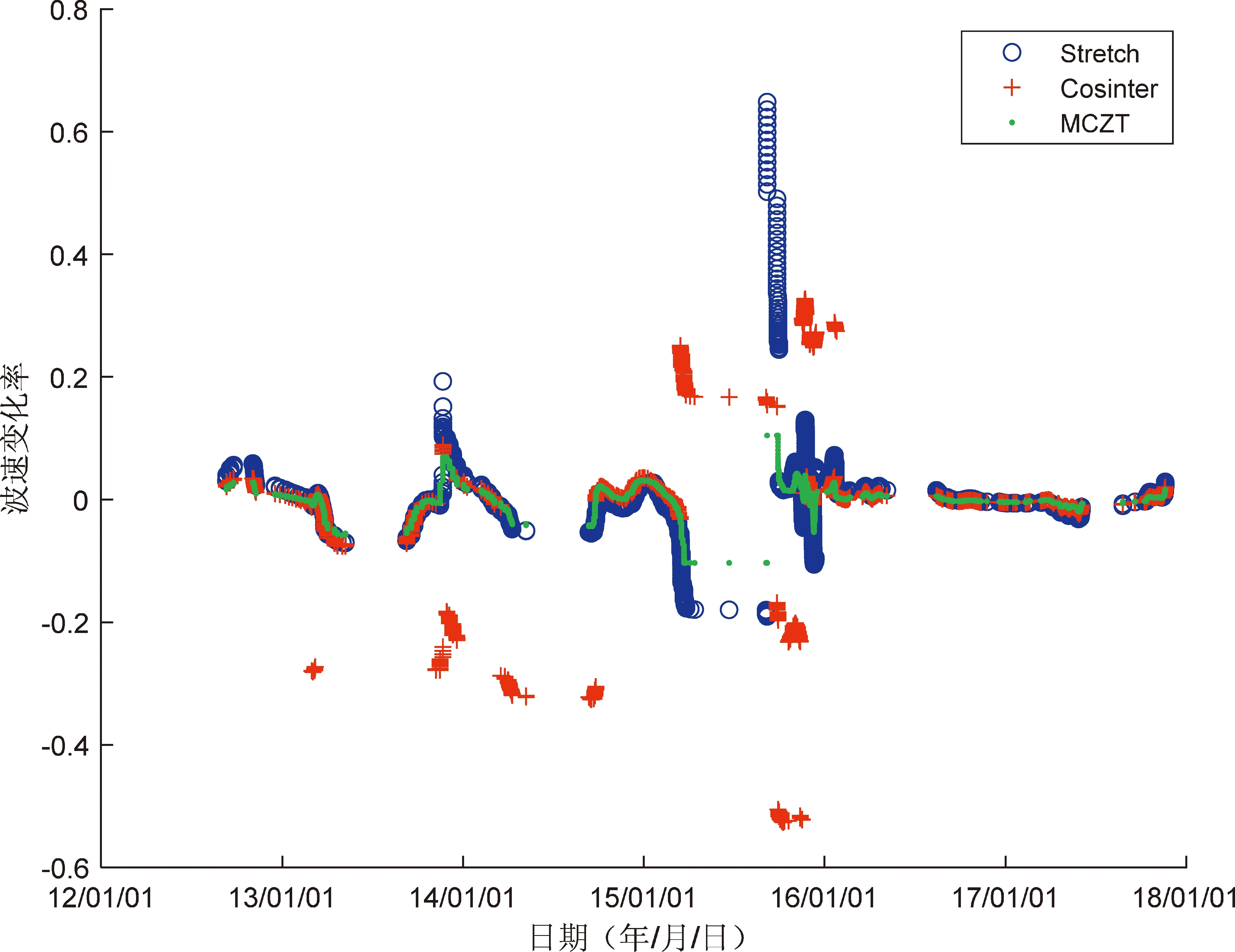
图9 53284台波速变化率Fig.9 Wave velocity change rate of the station 53286
对得到的去噪信号剔除信噪比较低的信号后,得到6 816条记录,最后得到信噪比较高、一致性较好的6 816条去噪记录。对时窗范围为10.0~11.3 s 信号,用3种方法分别计算其波速变化,以三者的结果平均值作为参考(标准)波速变化,然后以10.60 s为开始、步长为0.02 s,与数值模拟方法一样,分别计算不同窗长与恢复度的关系(图10)。计算结果表明:随窗长的增大,3种方法得到的波速变化的恢复度均升高,本文方法略优于余弦插值法,伸缩法最低。
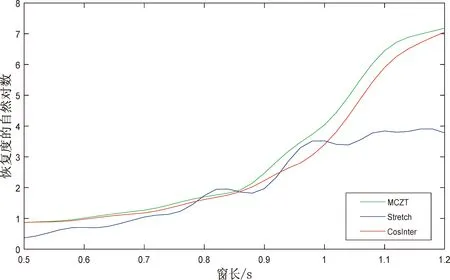
图10 53284台波速恢复度与计算信号窗长的关系Fig.10 The relationship between wave velocity recovery and the calculated signal window length at the station 53284
5 结论
本文根据地下介质波速变化测量精度的需求和宾川气枪主动源数据特点,介绍了一种能够在短时窗互相关计算中获得高精度时延估计的方法,通过实验对比分析,得到以下结论:
(1)基于MCZT和FICP的时延估计方法可以得到较高精度的时延估计值,通过模拟实验表明,该方法较余弦插值法有一定的提升,明显优于伸缩法。
(2)本文方法在短时窗互相关时差计算中优势较大,且在走时差计算过程中,通过使用MCZT,只计算有用信号所在频段,实现对噪声干扰的抑制,提高了地震信号时延估计的精度。
(3)利用FICP相关峰精确插值方法,克服了传统方法插值结果不能完全反映相关峰形状、插值计算而带来信号误差、增加运算量等问题,提高了相关峰顶的分辨率,特别是对低采样信号优势明显。
(4)实际数据计算表明,本文方法略优于余弦插值方法,也具有一定的抗噪能力。
