建筑结构风振响应监测数据处理方法研究

郁 雯 何浩博

(1.河北省土木工程诊断、改造与抗灾重点实验室，河北 张家口 075000；2.河北建筑工程学院，河北 张家口 075000；3.中国铁路设计集团有限公司，天津 300142)

当今社会，随着科技水平的不断提高，建筑结构监测技术及数据处理方法也在不断革新，除了对传统的水准仪、全站仪及加速度计等在监测技术及数据处理方法上的探究外，国内外学者也同时对导航系统三维监测技术及滤波去噪技术进行了分析.

伊晓东[1]、贺志勇等[2]分别以超高层钢结构建筑及塔高610m的在建电视塔为研究对象，采用基于RTK技术的GPS导航系统监测结构在强风作用下的风振位移数据，并与有限元模拟监测数据进行对比分析，结果表明：GPS-RTK技术实测数据与有限元模拟数据之间互差仅为8%，具有定位准，精度高的特点；李宏男等[3]同样采用GPS-RTK技术进行风振监测，以显著水平估计法对监测数据进行去噪处理分析得滤波振动曲线，并与有限元数值分析进行对比，结果表明：滤波技术在建筑结构风振等非线性信号的处理中适用性极高；吉绪发等[4]为了减小GPS监测多路径误差对试验数据的影响，对比分析了小波去噪法及Vondark去噪法的作用特性，并详细阐述了它们的优缺点，结果表明：两种去噪方法都可以在一定程度上减小监测误差，其中较小波去噪法，Vondark去噪可以更大程度上接近原始信号，且可以有效避免端部效应，但是计算效率较低；黄丁发等[5]同样对小波去噪法进行了多尺度分解研究，分离出微小振动影响源，从而提高数据采集精度；伊廷华等[6]针对GPS监测系统数据异常范围难确定的问题，基于仿真模型分析提出了一种关联负选择检测算法，结果表明：该检测算法可以以较少的检测器检测到较大的空间范围，在很大程度提高了检测效率.

综上所述，国内外研究学者关于导航系统监测风振响应数据的方法多数采用单星系监测，且多以GPS监测为主，对于数据去噪处理也有一定分析，但关于EMD滤波去噪处理的作用特性分析较少，因此本文以117大厦为风振监测对象，对比分析了基于GNSS-RTK技术的多星系组合导航系统的定位监测特性，并着重分析了EMD滤波去噪法的作用特性.

1 试验概况

本文采用现场实测的方法，以中国第一高楼天津高银117大厦为试验对象，如图1大厦立面图所示，该大厦属于典型的框架结构，其建造方正对称，以其总建筑面积84.7万平方米达世纪高楼建筑面积之最，其主体塔楼结构首层建筑面积达4200m2，并以0.88°渐变角度向上逐层递减，直至顶层减为2100m2，其地上建筑117层，高度达596.5m，地下建造有三层地下室结构，成为中国建筑第一高.

本文在大厦核心筒顶层四个角分别布设1～4号监测点，进行不同组合星系监测其X向及Y向的风振响应曲线，并通过EMD滤波去噪法进行数据处理，具体布设情况如图1测点平面布设图所示.

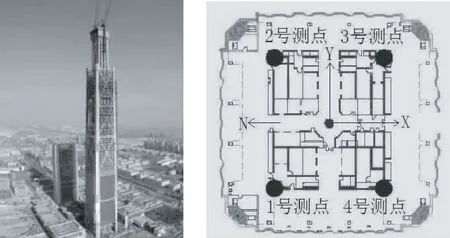
图1 117大厦立体图及测点平面布设图

2 GNSS-RTK定位监测技术

2.1 GNSS-RTK定位机理

GNSS是包括诸如GPS、GLONASS、BDS等众多导航系统及相应增强系统的一种全球卫星，其主要组成部分包括用户设备、空间星座及平面监控等[7-8]，如图2所示，GNSS技术定位原理即通过确定各卫星空间坐标S1(X1,Y1,Z1)、S2(X2,Y2,Z2)、S3(X3,Y3,Z3)及卫星与接收机之间的中心距离ρ1、ρ2、ρ3，同时考虑到多星系导航系统的时间与空间标准存在差异性，因此本文通过等效伪距修正的方法实现时空统一，从而组合导航解算出接收机所处的位置P(X,Y,Z)[9].

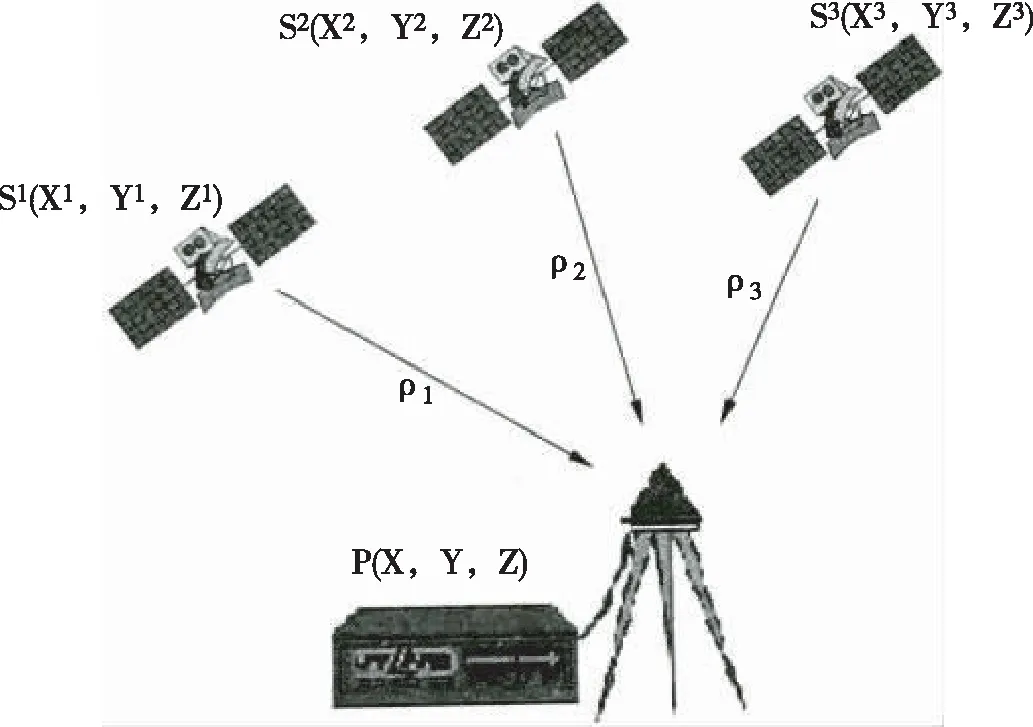
图2 GNSS定位原理示意图

RTK技术原理即通过设置一台接收机作为基准站和多个接收机作为移动站，将与基准站连接好的移动站分别布设在要进行监测的测站位置，进行实时监测时，基准站与移动站同时接受卫星信号，从而获得各测点实时三维动态数据信息，进行统计整理分析.

2.2 GNSS-RTK测量精度及稳定性试验

本试验主要以最为常见的GPS、GLONASS及BDS导航系统多组合星系监测为研究对象，接收机采用海星达H32五台，其中一台作为基准站，编号Q，其它四台作为移动站，分别编号为A、B、C、D，移动站A采用GPS一星系导航监测系统；移动站B采用GPS+GLONASS二星系导航监测系统；移动站C采用GPS+BDS二星系导航监测系统；移动站D采用GPS+GLONASS+BDS三星系导航监测系统，各组合星系监测系统同时进行连续数据采集3000s，进行数据处理，从而进行对比分析，试验布置现场如图3所示.

图3 GNSS-RTK精度试验布置现场

由现场精度测试试验得出不同组合星系导航系统的平面中误差mx与my，高程中误差mz，PDOP值及卫星数量等，其中PDOP表示位置精度强弱度，其大小可用来评价卫星组合分布好坏，其值越小，代表卫星组合分布越好，试验结果如下表1所示.

表1 不同星系组合试验数据

由表1，随着星系组合数的增多，高程中误差mz及PDOP值不断减小，卫星数不断增多，单星系导航系统平面中误差mx及my相对较大，二星系与三星系组合导航系统平面中误差mx及my大小差异不大，由此可知，单星系导航系统定位精度最差，三星系组合导航系统相对于单星系或二星系来说，定位精度最高，空间几何分布最稳定，适用性极强.

3 EMD滤波去噪技术应用

如图4所示为GNSS-RTK监测技术中GPS+GLONASS+BDS三星系导航系统测得的测点处X向及Y向的实时振动曲线.

由图可知，三星系实时振动曲线在X向及Y向振动幅度相当，差异性较小，且其振动曲线表示的规律不太明显，针对此现象，本文采用基于自相关函数的EMD滤波去噪法进行数据处理，从而进行有效的分析.

EMD滤波去噪法对风振响应等非线性信号采集处理适用性极强，其基本原理即通过将复杂的信号由高频到低频分解为若干个本征函数，简称IMF，然后从这些本征函数中分离出噪声，将去噪后的各个分量进行重组，即可得到去噪后的信号，具体解算原理如下所示.

(1)对于非线性信号Xi(t)，设r0=Xi(t)，i=1；

(2)从第i个非线性信号中获取IMF信号，数据处理步骤如下：

①h0(t)=ri(t)，k=1；

②提取hk-1(t)的极大值及极小值序列；

③采用插值法拟合hk-1(t)极值点序列，从而获得上、下包络线值uk-1(t)和vk-1(t)；

④由式mk-1(t)=(uk-1(t)+Vk-1(t))/2计算均值曲线；

⑤计算hk(t)=hk-1(t)-mk-1(t)；

⑥确定是否满足迭代准则，若满足则IMFi(t)=hk(t)，若违背则重复②～⑥，直至满足为止；

(3)计算剩余信号：ri(t)=ri-1(t)-IMFi(t)；

(4)若ri(t)的极值点数>2，则i=i+1，并循环第(2)步，否则分解结束，此时ri(t)即为残余信号分量；

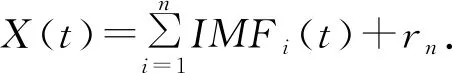
为了验证基于自相关系数的EMD滤波去噪法的适用性，本文对如图4所示三星系组合导航系统测得的振动信号进行数据处理，以X向为例进行分析，首先通过解算原理公式确定X向非线性振动信号的分解曲线如图5所示，然后确定各阶IMF分量的归一化自相关函数，以F1～F9表示，X向各IMF分量自相关函数如图6所示.

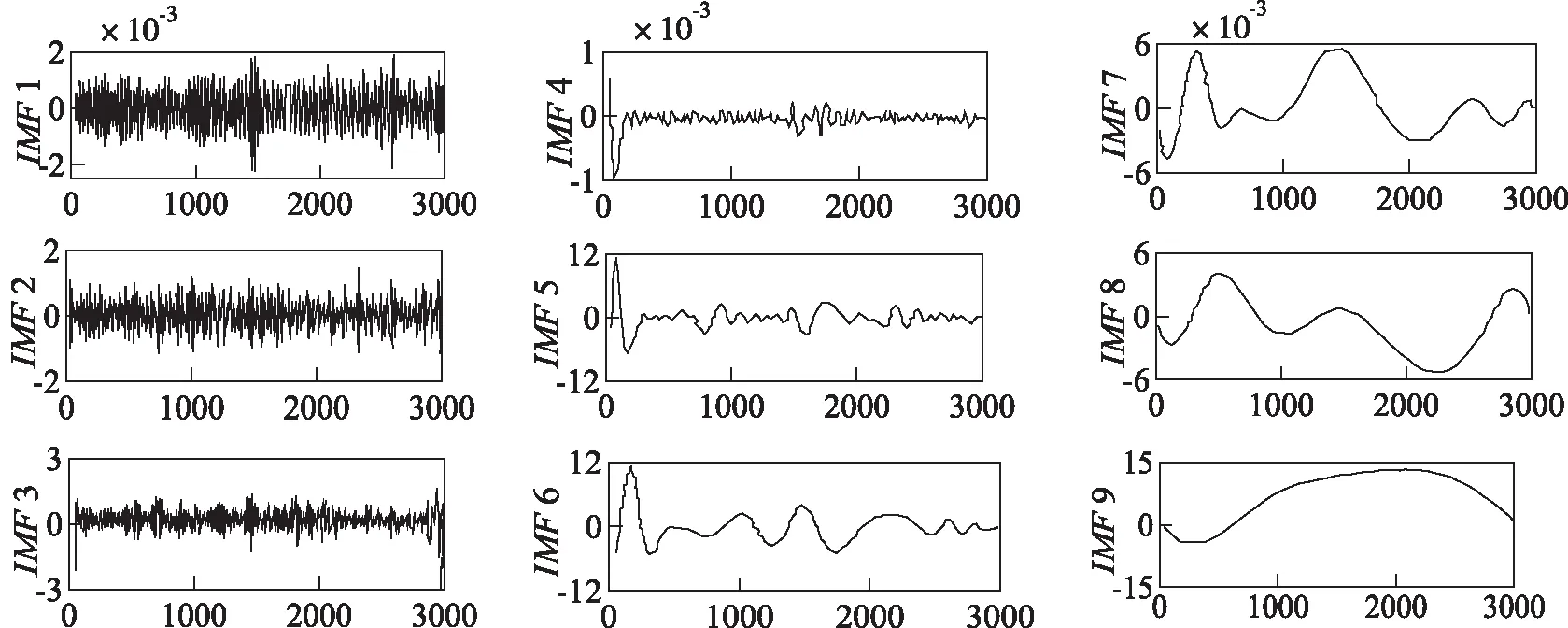
图5 X向各IMF分量

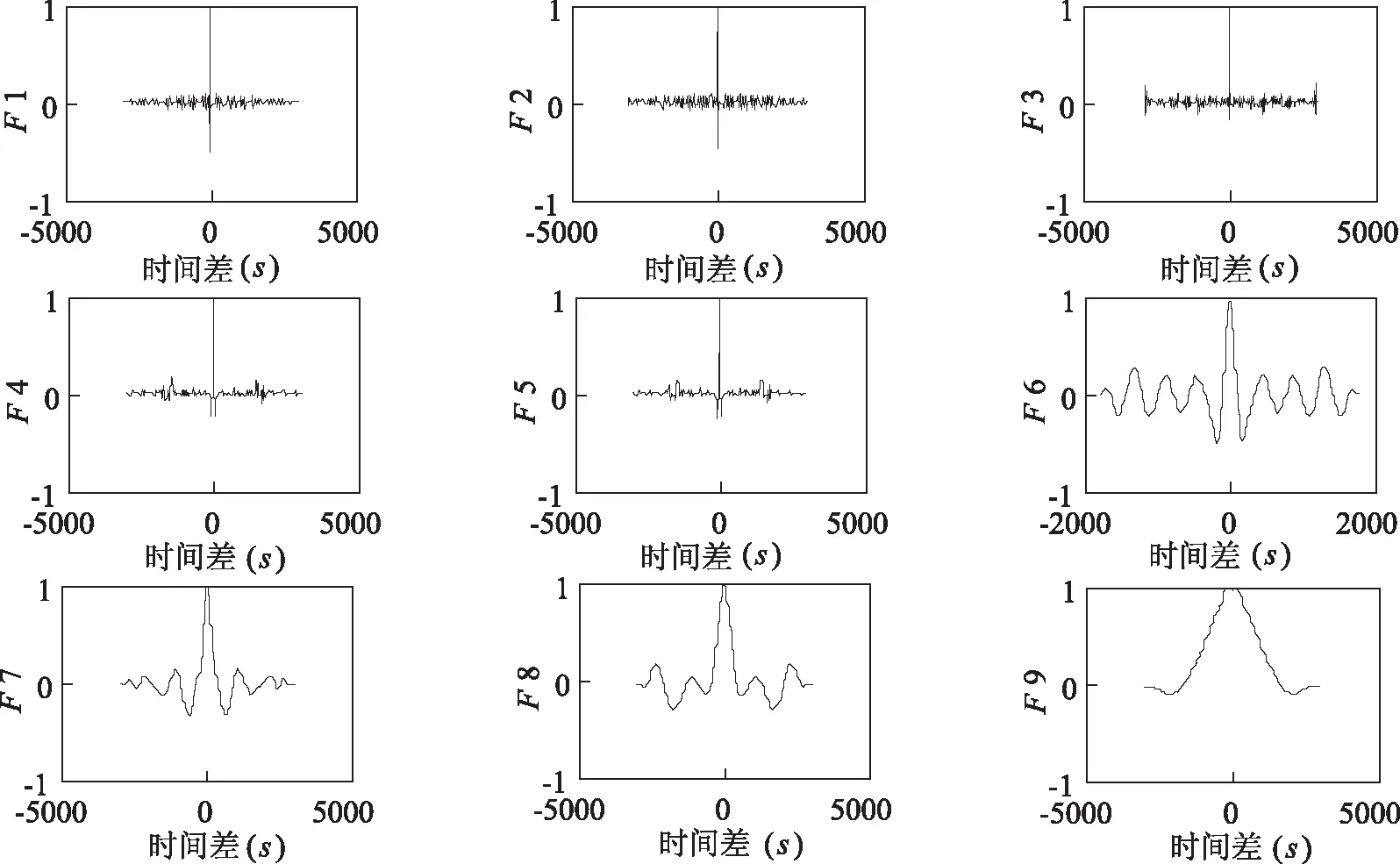
图6 X向各IMF分量自相关函数

由图6发现，F1～F5对应图，其均在时间差为零值处取得最大值，而其相邻时间差位置处F值迅速衰减到特别小，由此可知，F1～F5对应阶数在原振动信号中噪声起主导作用，因此在信号去噪处理过程中，只需要对前五阶进行去噪处理即可，然后将处理后信号与其余几乎不受噪声影响的信号进行重组，得到重构去噪曲线如图7所示.

图7 基于自相关函数EMD滤波后振动曲线

由图7与去噪前的图4对比发现，经去噪处理后X及Y向的振动曲线的振幅明显减小，且X与Y向的振动曲线的差异性也更为清晰，即Y向振幅相对X向更小，由此可见EMD滤波去噪法可以很大程度降低试验数据监测误差，提高测量精度，具有极强的适用性.

4 结 语

(1)基于GNSS-RTK技术的GPS+GLONASS+BDS三星系组合导航监测系统相对于单星系及二星系导航监测系统来说有更高的定位精度，更好的稳定性，可以很好的应用于工程实例.

(2)EMD滤波去噪法是基于数据本身去噪处理的一种方法，其计算效率高，与原始信号吻合度高，可以很好的反应风振等非线性信号的规律，从而做到有效的分析.