基于应力敏感效应和启动压力梯度的双重介质低渗油藏邻井干扰试井模型
2020-04-30姜瑞忠崔永正毛埝宇刘秀伟李盈盈
姜瑞忠, 高 岳, 崔永正, 毛埝宇, 刘秀伟, 李盈盈
( 1. 中国石油大学(华东) 石油工程学院,山东 青岛 266580; 2. 中国石油大学(华东) 机电工程学院,山东 青岛 266580 )
0 引言
在油气藏开发过程中,一口井的测试资料在后期容易受邻井的干扰,导致试井曲线上的压力导数曲线“上翘”。普通的单井试井方法未考虑测试井在邻井干扰下的压力响应动态,在试井资料解释中,经常将后期“上翘段”处理为封闭断层[1-3]。
对于无限大均质油藏,THEIS C V[4]推导中心点受其他点流速变化引起的压力解。在East Texas Field和Silica Pool两个油田,ELKINS L F[5]进行干扰试井的现场应用。DERUYCK B G等[6]建立双重介质油藏干扰试井模型,利用图版拟合解释井间干扰。张秀华[7]考虑井筒储集和表皮效应,建立复合油藏干扰试井模型,绘制相应的图版。为解决气藏中测试井容易受邻井生产干扰问题,孙贺东[8]建立邻井干扰条件下的邻井试井模型,受邻井的干扰,测试井出现多个径向流段,在压力导数曲线后期出现“下掉”现象。程时清等[9]建立多井干扰试井模型,判断多级压裂水平井见水方向并确定井间连通情况。HE Y等[10]建立非对称多裂缝水平井多井干扰模型,对相关参数进行敏感性分析。在干扰试井解释中,MOUSLI N A[11]研究地层裂缝对测试井和干扰井井底压力的影响。
人们研究邻井干扰下的试井情况,建立相应的邻井干扰试井物理模型和数学模型,绘制理论图版[12-16],但大部分研究建立于均质油藏或普通的多重介质油藏,未考虑低渗油藏的应力敏感效应和启动压力特性。笔者考虑储层应力敏感效应和启动压力梯度,建立双重介质低渗油藏邻井干扰试井模型,研究双重介质储层应力敏感效应和启动压力梯度对邻井干扰试井的影响,为低渗油藏邻井干扰试井解释提供指导。
1 模型建立
一口测试井位于无限大双重介质低渗油藏中心,距离测试井r1的位置,存在一口以定产量q生产的邻井,考虑应力敏感效应和启动压力梯度,建立双重介质低渗油藏邻井干扰试井物理模型(见图1)。

图1 双重介质低渗油藏邻井干扰试井物理模型Fig.1 Physical model of interference well test of adjacent well in dual medium low permeability reservoir
假设条件:油藏边界无限大;采用Warren-Root模型,流体从基质向裂缝窜流为拟稳态窜流;孔隙中流体微可压缩,忽略重力和毛管力的影响;裂缝和基质的渗透率比为常数;裂缝流向井筒为径向流动;孔隙渗透率考虑应力敏感效应;流体在孔隙中流动存在启动压力梯度;测试井考虑井筒储集效应和表皮效应,邻井不考虑井筒储集效应和表皮效应[17-22]。
考虑裂缝应力敏感效应和启动压力梯度的运动方程[23-27]表示为
(1)
式中:vf为流体在裂缝中的流动速度;Kf为裂缝渗透率;μ为原油视黏度;pi为初始地层压力;pf为裂缝压力;r为半径;λB为启动压力梯度;γ为应力敏感系数。
根据物理模型,考虑应力敏感效应和启动压力梯度,建立双重介质低渗油藏邻井干扰试井模型:
(2)
式中:φf为裂缝孔隙度;φm为基质岩块孔隙度;Ctf为裂缝综合压缩系数;Ctm为基质综合压缩系数;Vf为裂缝体积比;Vm为基质体积比;Km为基质渗透率;pm为基质压力;α为基质岩块形状因子;t为时间。
式(2)变形为
(3)

(4)
将量纲一的变量代入式(4),得到量纲一的渗流微分方程为
(5)
初始条件为
pfiD(riD,0)=pmiD(riD,0)=0。
(6)
外边界条件为
pfiD|riD→∞=pmiD|riD→∞=0。
(7)
测试井内边界条件为
(8)
邻井内边界条件为
(9)
2 模型求解
采用Pedrosa变量代换和正则摄动法消除方程的非线性:
(10)
式中:ξD为摄动变形函数。
由于γD=1,取零阶摄动解,再进行Laplace变换,式(5)变为
(11)
式中:s为Laplace变量;ξD0i为零阶摄动解;i=1、2,1为测试井,2为邻井。
将式(11)化简为
(12)
定义
(13)
将式(13)代入式(12)可得
(14)
根据Bessel原理,求得井底的压力通解为
(15)
(16)
式中:A、B为中间变量;I0、K0分别为零阶第一类和第二类虚宗量Bessel函数。
将式(11)代入式(15),求得测试井井底压力为
(17)
式中:K1为一阶第二类虚宗量Bessel函数。
邻井在测试井处的压力为
(18)
式中:rD1为邻井到测试井的量纲一的距离;qD1为量纲一的邻井产量。
利用Duhamel原理和压降叠加原理,在邻井干扰下,考虑井筒储集效应和表皮效应的测试井井底压力解为
(19)
式中:S为表皮因数。
通过Stehfest数值反演,得到考虑应力敏感效应和启动压力梯度的双重介质邻井干扰下的量纲一的压力解为
(20)
3 模拟结果
3.1 流动阶段划分
考虑应力敏感效应和启动压力梯度,双重介质低渗油藏邻井干扰的井底压力响应曲线见图2。根据曲线特征划分7个流动阶段,流动阶段特征见表1。
3.2 参数敏感性分析
3.2.1 井筒储集系数
井筒储集系数CD对井底压力响应曲线的影响见图3。由图3可以看出,井筒储集系数越大,续流阶段持续的时间越长,裂缝径向流阶段压力导数曲线发生倾斜,较大的井筒储集系数掩盖裂缝系统径向流。

图2 双重介质低渗油藏邻井干扰的井底压力响应曲线
Fig.2 Bottom-hole pressure response curves of adjacent well interference model for dual media low permeability reservoirs

图3 井筒储集系数对井底压力响应曲线的影响Fig.3 Effect of CD on bottom-hole pressure response curves

表1 不同流动阶段的渗流特征
3.2.2 邻井产量
邻井产量qD1对井底压力响应曲线的影响见图4。由图4可以看出,第一径向流阶段为生产井自身的反映,未受邻井的干扰;第二径向流阶段为测试井与邻井的共同反映。邻井产量越大,第二径向流段越高,第二径向流段的压力导数与qD1呈正相关关系,关系式为y=(1+qD1)×0.5。
3.2.3 应力敏感系数
应力敏感系数γD对井底压力响应曲线的影响见图5。由图5可以看出,应力敏感系数对压力及压力导数曲线的影响开始于表皮阶段。考虑应力敏感效应,储层渗透率受压力梯度影响而降低,流体流动阻力增大,压力导数曲线比不考虑应力敏感效应的曲线位置上移,并且应力敏感系数越大,上移幅度越大。随渗流的发生,近井地带压力梯度逐渐变大,渗透率下降幅度变大,压力导数曲线表现为流动后期比前期上翘幅度更大。
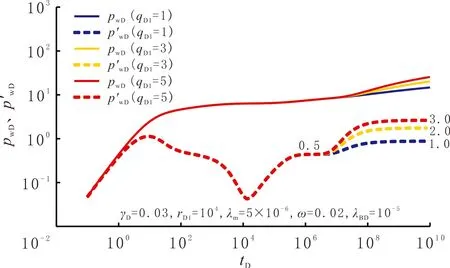
图4 邻井产量对井底压力响应曲线的影响Fig.4 Effect of qD1 on bottom-hole pressure response curves

图5 应力敏感系数对井底压力响应曲线的影响Fig.5 Effect of γD on bottom-hole pressure response curves
3.2.4 启动压力梯度
当储层存在启动压力梯度时,流体需要更大的驱动压力克服孔壁存在的渗流阻力。启动压力梯度λBD对井底压力响应曲线的影响见图6。由图6可以看出,启动压力梯度造成压力导数曲线上翘,启动压力梯度越大,上翘幅度越大,尤其在受邻井干扰的第二径向流阶段上翘幅度更明显。
3.2.5 邻井距离
邻井距离rD1对井底压力响应曲线的影响见图7。由图7可以看出,邻井距离越近,第二径向流阶段开始时间越早,第一径向流阶段持续时间越短,应力敏感效应和启动压力梯度对第二径向流阶段影响越明显,压力导数曲线上翘幅度越大。
3.2.6 窜流因数
窜流因数主要影响基质向裂缝的窜流阶段。窜流因数λm对井底压力响应曲线的影响见图8。由图8可以看出,窜流因数越小,流体从基质向裂缝窜流阻力越大,发生窜流需要的压力梯度越大,基质向裂缝窜流阶段发生时间越晚,在压力导数曲线上表现为“凹子”右移,但“凹子”的深度和宽度基本不变。

图6 启动压力梯度对井底压力响应曲线的影响Fig.6 Effect of λBD on bottom-hole pressure response curves

图7 邻井距离对井底压力响应曲线的影响Fig.7 Effect of rD1 on bottom-hole pressure response curves
3.2.7 弹性储容比
弹性储容比ω对井底压力响应曲线的影响见图9。由图9可以看出,弹性储容比主要影响第一径向流之前的流动阶段。弹性储容比越大,裂缝中储集流体的能力越强,基质向裂缝窜流需要的压力梯度越大,窜流量越小。随弹性储容比的增大,基质向裂缝窜流阶段滞后,在压力导数曲线上 “凹子”变浅、变窄。

图8 窜流因数对井底压力响应曲线的影响Fig.8 Effect of λm on bottom-hole pressure response curves

图9 弹性储容比对井底压力响应曲线的影响Fig.9 Effect of ω on bottom-hole pressure response curves
4 实例分析
应用文中邻井干扰试井模型,对实际压力恢复资料进行试井解释步骤:(1)利用收集到的压力恢复资料,绘制压力及压力导数曲线。分析压力响应曲线后期是否存在多个径向流段,是否符合邻井干扰试井曲线的特征。如符合邻井干扰试井曲线的特征,采用邻井干扰试井模型进行参数解释;否则,采用普通单井试井模型。(2)根据试井解释模型(未考虑应力敏感效应和启动压力梯度影响),通过改变井筒储集系数、表皮因数、窜流因数和弹性储容比对初期压力响应曲线进行拟合。(3)利用邻井干扰试井模型,设置不同邻井距离、邻井产量,对后期多段径向流段进行拟合解释。(4)将常规油藏邻井解释结果参数作为初始参数,输入文中邻井干扰试井模型,通过改变应力敏感系数和启动压力梯度,对井底压力响应曲线进一步拟合解释,最终求得相关参数。
对新疆某低渗油田进行压力测试,测试井产量为21 m3/d,距测试井200 m处有一口产量为52 m3/d的油井。实测数据与文中邻井干扰试井模型模拟结果见图10。该井实测压力导数曲线在后期出现由邻井干扰导致的上翘,两口井连通性较好。若采用普通油藏邻井干扰模型进行拟合,第一径向流以后阶段,压力导数曲线明显低于实测压力导数曲线,对试井曲线拟合效果较差。由图10可以看出,采用文中邻井干扰试井模型拟合效果较好。地层压力为15.3 MPa,弹性储容比为1.6×10-2,窜流因数为2.1×10-6,启动压力梯度为4.68×10-5MPa/m,应力敏感系数为3.6×10-2MPa-1。

图10 某低渗油田实测数据与邻井干扰试井模型模拟结果对比
Fig.10 Comparison between measured data and simulation results of adjacent well interference test model from an oilfield
5 结论
(1)考虑应力敏感效应和启动压力梯度,建立双重介质低渗油藏邻井干扰试井模型。应用Pedrosa代换格林函数及叠加原理等方法求解模型,得到真实空间下的井底压力解,绘制井底压力响应特征曲线。
(2)根据井底压力响应曲线,将邻井干扰试井模型渗流过程划分为续流、表皮、裂缝径向流、基质向裂缝窜流、第一径向流、过渡流、第二径向流7个流动阶段。
(3)应力敏感效应和启动压力梯度对井底压力导数的影响开始于表皮阶段,压力导数曲线“上翘”,第二径向流段(即邻井影响阶段)的“上翘”幅度明显高于之前的流动阶段的;受邻井的干扰,测试井的压力导数曲线在后期“上翘”,出现两段径向流段,且两段径向流高度比等于两口井总产量与测试井产量之比。
