舰船装备软件可靠性验证与评价技术研究
2020-04-30沈晓美吴立金詹红燕韩新宇唐龙利
沈晓美,吴立金,詹红燕,韩新宇,唐龙利
(中国船舶工业综合技术经济研究院,北京 100081)
0 引言
在现代化战争中,武器在实战过程的强弱与软件可靠性直接关联。舰船装备软件具备接口数据类型多、复杂网络环境等特殊性,为软件可靠性验证带来挑战。目前,舰船装备软件的可靠性验证和评价主要分为定性、定量两个方面。
软件可靠性定性要求的验证研究多以失效模式为基础,形成定性检查单,设计测试用例验证软件是否满足要求。可靠性定性要求的相关研究多从异常测试数据、故障注入角度出发,缺乏有效的手段。
软件可靠性定量指标主要通过可靠性测试、可靠性评估完成验证。目前软件可靠性评价相关标准只有《GJB/在161-2012军用软件可靠性评估指南》,其中提出的可靠性模型用于软件可靠性增长测试,不完全适用于软件可靠性验证测试。可靠性验证研究存在针对某些典型软件的贝叶斯验证优化模型,对舰船装备软件不具备通用性。
该文提出了4种软件可靠性验证方案,明确测试结束方式及通过标准,通过软件可靠性验证测试结果对软件可靠性进行评价,为舰船装备软件提供一种普适性软件可靠性验证与评价方法。
1 概念与研究现状
1.1 软件可靠性相关概念
软件可靠性是指在规定的条件下和规定的时间内,软件不引起系统故障的能力/概率。
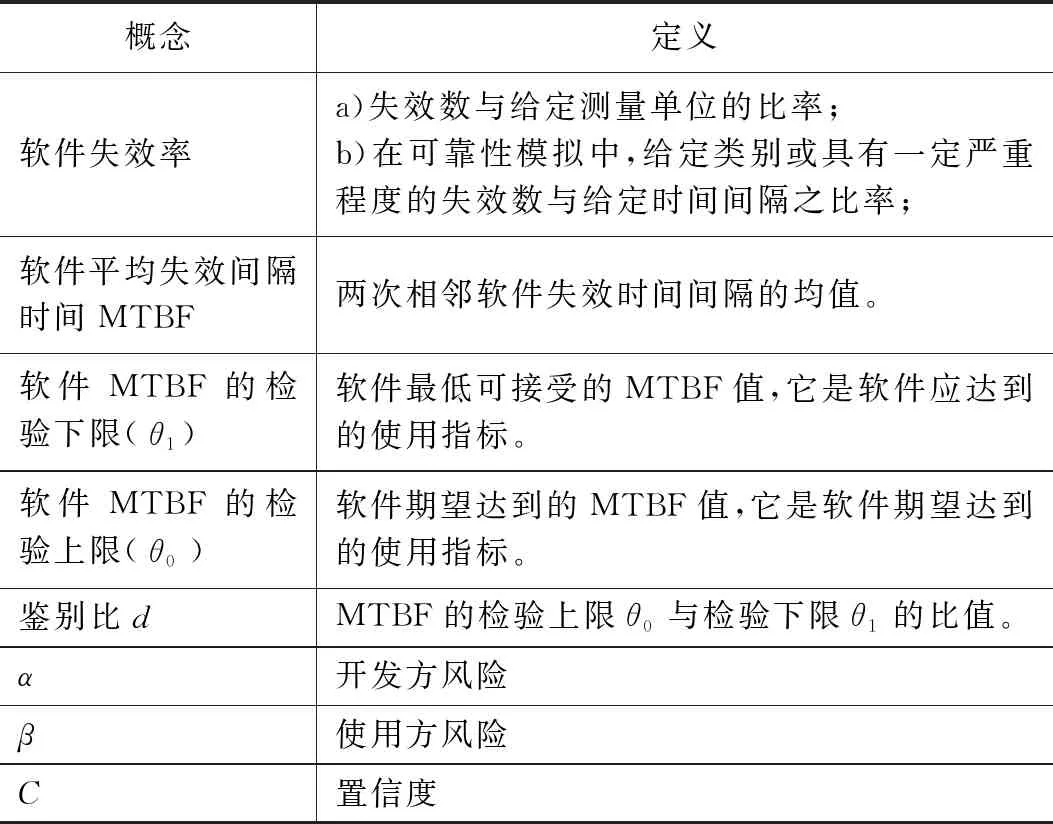
表1 软件可靠性相关概念
1.2 软件可靠性验证技术发展现状
软件可靠性验证技术主要从定性验证、定量指标验证两个方面进行研究。
1.2.1 软件可靠性定性验证技术
软件可靠性定性验证是指根据软件的缺陷信息设计可靠性测试用例,判断软件是否满足任务书提出的接口容错性要求、界面健壮性要求、数值边界性要求以及可靠性措施等软件可靠性定性要求是否满足要求。
目前软件可靠性定性验证主要分为两个研究方向:一是收集软件的缺陷模式(如需求设计类缺陷、功能类缺陷、接口类缺陷、代码类缺陷),从缺陷模式角度设计用例验证软件定性要求;二是研究不同故障注入的方式(如代码变异算子、硬件故障等)验证软件健壮性等定性要求。
1.2.2 软件可靠性定量验证技术
软件可靠性定量验证是指利用软件可靠性验证测试结果对软件的可靠性进行定量评价。
目前软件可靠性定量验证技术研究方向主要为软件可靠性建模及其优化,从可靠性验证模型、剖面获取模型、测试方法等方面进行深度研究。如针对某软件贝叶斯可靠性评价模型、基于可靠度的测试方法、针对指标类型对不同可靠性模型优化等。现有软件可靠性定量验证研究方案对舰船装备软件不具有普适性。针对舰船装备软件交联环境复杂、接口种类多信息量大等特性,研究对舰船装备软件具有普适性的可靠性验证方案具有重要的实际意义。
2 研究方案
本文提出了4种软件可靠性验证测试统计方案,具体验证统计方案如图1所示。

图1 舰船装备软件可靠性验证与评价方案
1)基于舰船装备软件测试数据进行软件可靠性验证测试,测试执行过程从定时截尾方案、序贯测试方案、无失效运行方案、贝叶斯无失效测试方案进行。
2)软件可靠性验证方案选择策略。根据验证指标类型、可承受的最大测试时间、测试环境的预期寿命、可承受的最大失效数、该类型软件的质量要求等因素选择统计测试方案。
3)通过测试结果与统计测试方案中接收或拒收标准比较确定软件可靠性测试是否合格。
3 软件可靠性验证统计方案
3.1 定时截尾方案
定时截尾方案是指预先知道试验持续时间,可以在试验持续时间、使用方风险α和生产方风险β、检验上限θ0、检验下限θ1之间权衡,即对于给定的α、β、θ0、θ1,计算试验持续时间和接收故障数r。
3.1.1 定时截尾方案及其抽样特性
定时测试方案的MTBF的真值θ与接收概率P(θ)的关系,可用泊松公式表示为:
(1)
式中,r为方案接收时所对应的判决失效数;T为方案接收时所对应的判决总测试时间。
3.1.2 定时截尾方案使用步骤
1)根据合同要求得到θ0、θ1、α、β。并计算d=θ0/θ1;
2)根据上述参数查GJB 899中的表A.3和表A.4,得到相应的方案号。并从表中得到测试时间和判决失效数;
3)上述测试时间与θ1乘积为真实测试时间;
4)当实际测试时间T(小时)达到选定方案所对应的真实试验时间时,若测试的软件失效数小于拒收的判决失效时,则拒收;若测试所出现的软件失效数小于或等于接收失效数,则作接收判决。
3.1.3 定时截尾方案的置信度
MTBF的估计步骤如下:
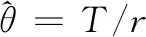
(2)
式中,T为设备总测试时间;r为软件失效数。
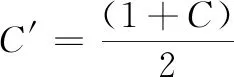
3)计算出MTBF的置信下限θL和置信上限θU:
(3)
4)MTBF的验证区间为:(θL,θU),(置信度C);
5) 若GJB 899中表A7的数据不足,可按下式计算出置信下限系数θL(C′,r)和置信上限系数θU(C′,r):
(4)
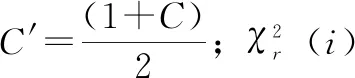
3.2 序贯测试方案
序贯试验统计方案包含标准统计方案、短时高风险统计方案两种。预期采用正常的生产方风险和使用方风险(10%~20%)时,应采用标准型统计方案。采用短时高风险统计方案,可以缩短试验时间,但生产方和使用方均承担较高风险。对于MTBF的真值较大或较小的产品,序贯试验所需的总试验时间差别较大,计划费用和时间应以序贯截尾的时间为依据。
3.2.1 序贯测试方案及其抽样特性
对于具有未知的MTBF值θ的指数型产品,在累计工作时间t内发生r次故障的概率为:
(5)
序贯试验须证明θ至少不小于MTBF检验下限θ1。本文采用判决标准见GJB899图A.1~图A.8。
3.2.2 序贯测试方案使用步骤如下:
1)根据合同要求得到θ0、θ1、α、β。并计算d=θ0/θ1;
2)根据上述参数查GJB 899中的表A.1和表A.2,得到相应的方案号。并按照表中的“判决标准”得到相应的图号;
3)根据得到的图号查相应的“接收-拒收判决标准”,并将表中的“标准化判决时间”乘以θ1得到不同失效数下的拒收判决时间TR和接收判决时间TA;
4)将受试设备的实际总测试时间T(小时)、软件失效数r逐次和判决值TA、TR进行比较。若T>=TA,则作出接收判决,停止测试;若T<=TR,则作出拒收判决,停止测试;若T介于两判决值TA和TR之间,则继续测试到下一个判决值时再比较,直到可以作出判决并停止测试时为止。
3.2.3 序贯测试方案MTBF置信限
序贯测试达到接收判决时,MTBF的置信区间或测试区间的置信度为C′的置信下限θ1和置信上限θ0按如式(6)计算:
θL=θL(C′,ti)θ1
θU=θU(C′,ti)θ1
(6)
式中,i为达到接收判决时的软件失效数;C′=(1+C)/2;θL(C′,ti)为置信度为C′,软件失效数为i时的置信下限系数,从GJB899表A5a中查出。θU(C′,ti)为置信度为C′,软件失效数为i时的置信上限系数。从GJB899表A5b中查出。MTBF的双边保守置信区间或验证区间则为:
(θL,θU),(置信度C)。
3.3 无失效运行方案
无失效方案主要用于对可靠性很高的软件进行验证测试,或对验证测试已判为接收的软件改错后进行的无失效交付测试。该方案根据在给定的测试时间内执行可靠性测试用例时软件有无失效来进行接收/拒收判断,即无失效时接收软件,有失效时拒收软件。
3.3.1 无失效测试方案及其抽样特性
直接将失效数r=0代入双风险公式:
T=-θ1lnβT=-θ0lnα
(7)
通常考虑使用方风险,则由第二式计算。β通常很小,则测试时间应比θ1稍大,若在此时间内软件不失效,则接收,否则拒收。
在不同风险下的测试时间见表2。
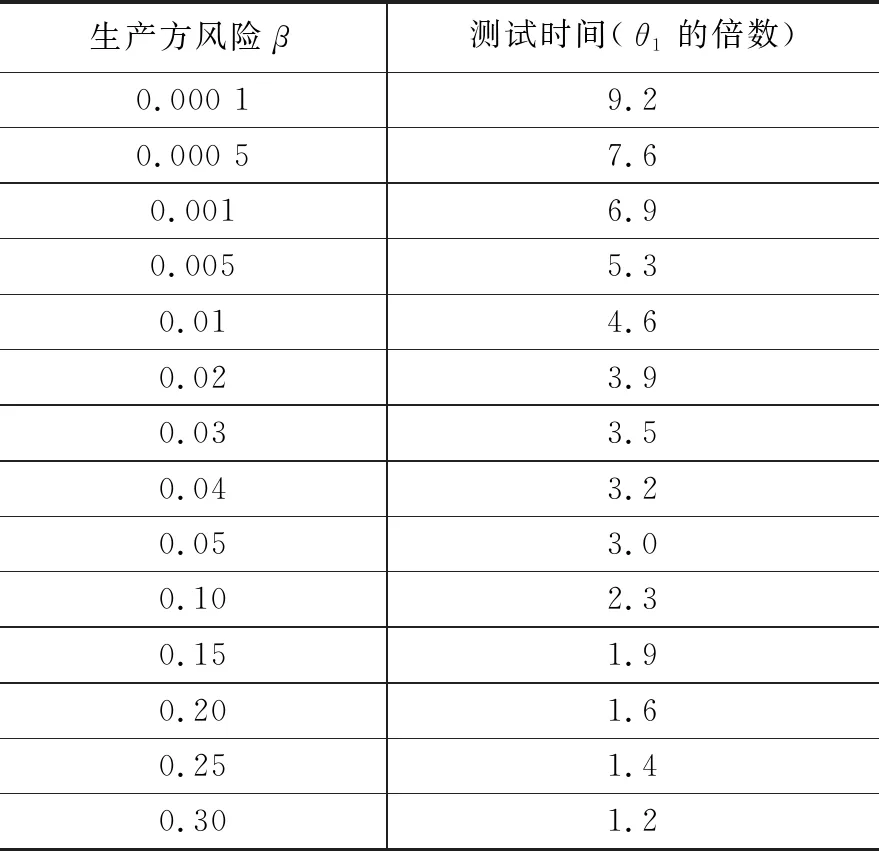
表2 无失效方案
3.3.2 无失效测试方案的使用步骤
1)根据合同要求得到θ1、β;
2)根据上述参数查表2,从表中得到测试时间;
3)用该方案的测试时间乘以θ1得到真实的测试时间;
4)测试时当实际总测试时间T达到选定方案所对应的真实的试验时间时,若测试中出现软件失效,则作出拒收判决;若测试中没出现软件失效,则作出接收判决。
3.4 贝叶斯(Bayesian)无失效测试方案
贝叶斯无失效测试方案是一种对失效率指标进行验证的测试方案,其基本思想是:首先利用给定的软件失效率指标λ0、置信度C以及软件可靠性测试中的先验信息来确定满足可靠性指标要求所需的无失效验证测试时间,并进行软件可靠性验证测试。若测试执行时间超过T后,软件没有发生任何失效,则验证测试通过,接收该软件;否则验证测试不通过,拒收该软件。当开发方修改软件失效所对应的缺陷后,想继续进行验证测试,则可以结合发生失效时的测试时间,重新计算此时所需要的无失效验证测试时间,重复上述验证测试过程,直至验证测试结束。该验证测试方法可以充分利用软件失效的先验信息,有效减少验证测试的时间。
3.4.1 Bayesian测试方案及其抽样特性
基于软件失效率指标λ0,置信度C已是确定值。贝叶斯方法是指软件失效率λ是一个随机变量,软件在时间区间(0,t]内失效次数x等于k的概率为随机变量λ的条件概率。即软件失效次数x服从参数为λt的泊松分布:
(8)
通过泊松分布的共轭分布为Gamma分布,得到失效率的先验分布函数:
(9)
假定软件持续运行时间为t,其间发生r次失效,则软件失效率的后验分布函数为:
h(λ|r,t,a,b)=Gamma(a+r,b+t)
(10)
根据式(8)和(9)可推导失效次数x的边缘分布为:
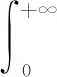
(11)
m(x)的一、二阶矩为:
(12)
(13)
通过式(12)和(13),可求出超参数a和b与软件失效数边缘分布的一阶矩和二阶矩之间的关系。
将软件在可靠性增长测试阶段的测试记录表示为失效间隔时间序列T1,T2,…,Tn。因此,若已知软件失效间隔时间序列的经验样本值,可以对a和b进行估计。
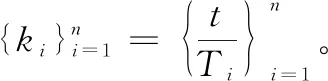
(14)
根据式(12)~(14),即可计算参数a和b的先验估计值a0和b0,进而得到软件失效率λ的先验分布函数为:
(15)
确定软件失效率λ的先验分布后,即可以对软件可靠性指标进行验证。设给定的软件可靠性指标为(λ0,C)。则满足相应可靠性指标的软件无失效验证测试时间t1取满足下式的t的最小值:
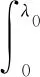
(16)
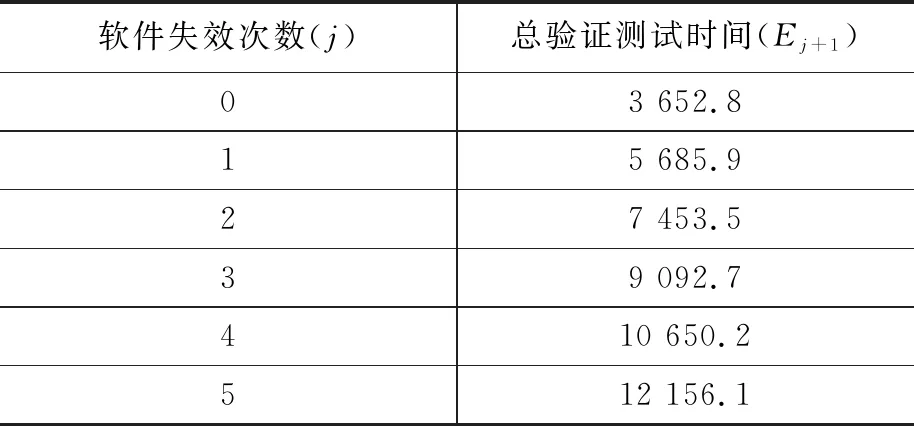
如果软件在该验证测试时间未发生失效,说明软件已经达到规定可靠性指标,可接收该软件;如果软件在tf1时刻(tf1 (17) 持续该计算过程,即如果在此过程中已发生第j次失效,那么第j+1次无失效验证测试时间tj+1取下式中t的最小值: (18) (19) 根据式(19)计算第j次软件失效对应软件所需要的总测试时间Ej+1,进而计算第j+1次无失效验证测试的持续时间: (20) 依据式(19)计算总测试时间Ej+1是定值。由式(20)可知:前j次失效情况直接影响第j+1次无失效验证测试时间tj+1的长短。 3.4.2 Bayesian测试方案步骤 1)给定软件失效率指标λ0,置信度C; 2)利用式(12)~(14)对式(9)中的超参数a和b进行估算; 3)根据步骤1)和2)中得到的结果,首先利用式(16)计算第一次测试所需要的无失效验证测试时间t1;然后再根据式(19)计算出软件失效数j与对应的总测试时间Ej+1; 4)根据方案中规定的时间进行可靠性验证测试,软件连续执行t1时间时,若没有发生失效,表明软件达到了规定可靠性指标,则接收软件,转步骤6);若在验证测试过程中,出现失效,则表明软件未达到规定的可靠性指标,拒收软件,该次软件可靠性验证测试结束,转步5); 5)若开发方修改了软件失效对应缺陷,并要求重新进行软件可靠性验证测试,则结合新发现失效(设失效数为j)时已执行测试时间,利用此时所对应总测试时间Ej+1计算此时所需要验证测试持续时间tj+1,重复步骤4),否则转步骤6); 6)验证测试结束。 选择统计测试方案时考虑因素包含验证指标的类型、该类型软件的质量要求、测试环境的预期寿命、可承受的最大失效数、可承受的最大测试时间、费用-时间的权衡、是否有先验信息等。 根据上节4种软件可靠性验证方案,本文归纳软件可靠性验证统计方案选择策略为: 1) 指标为MTBF/失效率的软件,若要求提供MTBF验证值,且有固定截止时间,则定时截尾测试方案优先; 2) 若事先未规定可靠性验证时间,仅希望尽早对MTBF作出接收或拒收判决时,可选择序贯测试方案; 3) 软件可靠性要求(MTBF)很高时,则无失效测试方案最佳; 4) 对于MTBF要求很高,且做过可靠性增长测试有先验失效信息的软件,则优选贝叶斯测试方案以减少测试时间。 某监测系统软件,其规定的可靠性指标为(λ0,C)=(10-3,0.99)。在可靠性增长测试阶段,其最后10组失效间隔时间Ti的值如表3所示。 表3 先验样本数据 h 由于示例软件有先验失效信息,对MTBF要求较高,故选用贝叶斯测试方案可靠性验证测试。 1)该软件给定的失效率指标为λ0=10-3,置信度C=0.99; 2)利用式(12)~(14)计算出式(9)中软件失效率先验分布Gamma函数的超参数估计值为a0=1,b0=952.4; 3)根据以上数据由(19)计算出所需的总验证测试时间与软件失效次数之间的对应关系如表4所示。可知当进行第一次验证测试时,所需要的无失效验证测试持续时间为t1=3652.8小时; 表4 总验证测试时间与失效次数之间的对应关系 h 4)根据方案规定的时间进行软件可靠性验证测试,软件在时刻tf1=2000小时发生失效,则软件没有达到规定的可靠性指标,拒收软件。 5)开发方排除了相应软件缺陷,要求进行第二次验证测试,则所需要的无失效测试运行时间为t2=5685.9-tf1=3685.9小时。软件在第二次验证测试时,在3685.9小时可靠性验证测试中没有发生失效,则该软件可靠性指标达到要求,接收该软件。 6)验证测试结束。 本文针对舰船装备软件可靠性验证周期长、效率低、缺少有效手段和依据等现状,提出了定时截尾方案、序贯测试方案、无失效运行方案、贝叶斯测试方案等四种软件可靠性验证统计方案,并根据影响验证的因素(验证指标类型、测试环境的预期寿命、该类型软件的质量要求、可承受的最大测试时间、可承受的最大失效数、费用-时间的权衡、是否有先验信息等)给出了不同侧重因素时软件可靠性验证统计方案的选择策略,为舰船装备软件提供一种普适性软件可靠性验证与评价方法。最后结合某检测软件给出实例应用,实践证明本文提出的舰船装备软件可靠性验证与评价方法切实可行,具有重要的工程意义。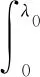
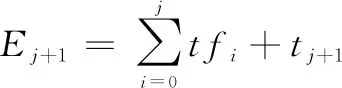
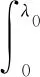
4 软件可靠性验证统计方案选择策略
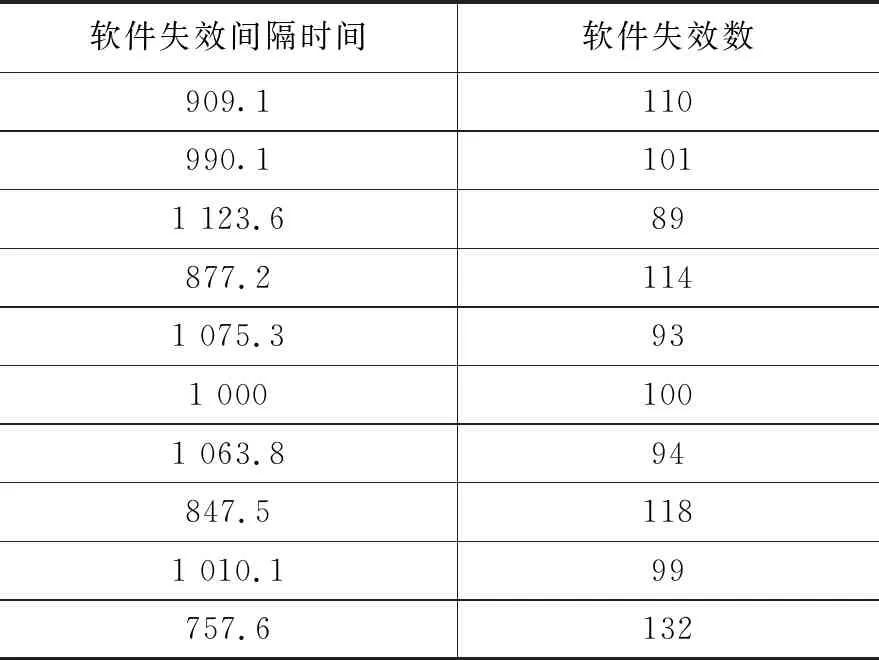
5 可靠性指标验证示例
6 小结
