基于PCA-RFR的传感器故障定位方法
2020-04-30赵忠盖
潘 磊,赵忠盖,刘 飞
(江南大学 物联网工程学院,江苏 无锡 214122)
0 引言
随着现代工业过程传感器检测的广度和深度逐渐扩展,基于数据驱动的故障检测和诊断方法也越来越具有吸引力,在保证工况安全运行的同时,还能有效地提高产品质量[1]。主成分分析(principal component analysis,PCA)作为一种常用的工业数据信息提取方法,可提取样本中的特征信息和残差信息,在过程监控中得到了广泛的应用[2]。PCA方法通过提取统计量对过程进行监控,若待检测样本统计量大于统计量控制限,则认为此时发生了故障[2-3]。在PCA方法检测到故障后需要对故障进行定位,典型的定位方法包括贡献图[4]、重构法[5]和重构贡献[6](reconstruction- based contribution,RBC)。这些故障定位方法认为变量贡献值越大越有可能是故障变量,然而由于受到拖尾效应的影响,一些非故障变量的贡献值同样增大并可能会超过故障变量贡献值,从而导致误诊[2]。基于PCA的传统故障定位方法的本质是基于数据之间的相关关系而不是因果关系[7],而这就使得其无法从根本上解决拖尾效应的影响,从而影响其在实际应用中的效果。
基于数据驱动的因果分析方法由于其在厘清变量之间因果关系中的作用,近些年来,开始逐渐应用在工业过程的故障定位与故障路径识别中。其中,文献[8]使用互相关函数法对带时滞的变量进行因果关系假设检验,但该方法仅适用于线性系统。针对非线性过程,文献[9]提出的传递熵(transfer entropy)因果分析方法对变量间传递的信息熵进行因果关系假设检验,但该方法易受噪声影响,且计算量大。对此文献[10]提出一种符号化传递熵(symbolic transfer entropy,STE)的因果分析方法,相比于传递熵中的核概率密度估计,该方法对序列进行符号化来得到变量的概率分布,从而大大减小了计算量,但该方法需要优化选择的参数较多,并且样本量较少时会影响估计的概率分布的准确性,从而影响最终预测的结果。由于基于数据驱动的因果分析方法都需要对变量进行逐对分析,当过程变量数为n,则需要求出n×(n-1)组变量之间的因果关系,然而实际工业过程故障发生后,在控制回路的作用下,收到故障影响的变量可能有限,这就会导致大量无用的计算,进而影响故障定位的效率。对此文献[7]提出一种利用重构贡献筛选出贡献率大的故障候选变量集,再针对平稳、非平稳变量序列,分别使用格兰杰因果(granger causality,GC)和动态时间规整(dynamic time warping,DTW)对筛选出来的变量集进行因果分析。与之相似,文献[11]提出使用lasso重构筛选故障候选变量集,再使用高斯回归进行故障因果分析。虽然这二种方法缩小了故障定位范围降低了计算量,但变量筛选是否可能会遗漏掉故障变量并不可知。文献[12]为降低计算量提出一种计算过程变量对于统计量的动态归一符号化传递熵(symbolic dynamic-based normalized transfer entropy,SDNTE)的故障定位方法,该方法仅需求得n组过程变量对于统计量的STE因果关系系数,从而显著缩小了故障定位所需花费的时间,但该方法使用的是STE方法来度量变量间的因果关系,存在前文所提的优化选择的参数过多、估计概率分布时对样本需求量大等限制。因此,在SDNTE方法的框架下,如何使用一种更加简洁并能适应于小样本集的方法对因果关系系数进行度量是一个值得研究的问题。
综上,本文在SDNTE方法的思路下提出一种基于PCA与随机森林回归算法(random forest regression,RFR)[13]相结合的PCA-RFR故障定位新方法,通过利用RFR的变量重要性度量得到过程变量对统计量的因果关系系数,辨识其中值最大的变量作为故障变量。相比于SDNTE方法,PCA-RFR无需优化选择参数,并且可以对小样本集建立良好的模型。最后通过一个数值仿真,并在TE过程仿真实验中将本文提出的方法与RBC、GC[7]和SDNTE方法的定位效果进行了对比,表明该方法定位效果的优越性。
1 基本理论
1.1 基于PCA的统计过程监控方法
PCA统计过程监控方法是将数据投影到二个正交的主元空间和残差空间上,并分别构建相应的检测统计量来进行监控过程运行状况的一种方法。
假设正常工况下的样本集为X∈Rn×m,n为样本数,m为变量数。标准化处理后,使其均值为0标准差为1。对协方差矩阵S奇异值分解得到:
(1)

任意一个样本可分解为:
(2)

PCA故障检测统计量指标包括T2、SPE以及φ统计量,其中φ统计量作为T2和SPE统计量的合成指标,使用起来更加方便简单[14]。
SPE统计量:
(3)
T2统计量:
T2(x)=xTPΛ-1PTx=xTDx
(4)
φ统计量:
(5)

1.2 RFR算法
随机森林(random forest,RF)算法是一种由很多学习器组成的集成学习算法,它通过数据的随机重采样(bootstrap)和结点随机分裂技术的应用来降低决策树之间的相关性,进而提高模型的预测性能。RF常用于分类和回归,基础学习器使用的是分类回归树(classification and regression tree,CART),它是一种结构为二叉树的决策树。
对于CART回归树的构建,假设x与y分别为输入和输出,并且是连续变量。在x所在的空间中,每个输入特征空间被递归的划分为二个子区域,并令每个子区域样本对应的y的均值作为输出值,使用平方误差最小化准则进行特征选择,构建二叉回归决策树。
RFR算法由多个CART回归树集成而成,具体建模过程如图1所示。利用bootstrap重采样出b组训练样本集xi(i=1,2,…,b)和相应的袋外数据(out-of-bag,OOB)集oobi(i=1,2,…,b),由于是等量随机重采样,其中每组训练样本集中会随机抽取到原始样本中约63%的样本,原始样本中剩余的37%样本即为OOB数据。OOB数据被用来进行模型测试以及变量重要性度量。将每组训练样本使用结点随机分裂技术生成CART回归树hi(i=1,2,…,b),并将生成的b颗决策树组成随机森林回归模型f={h1,h2,…,hb}。当对待检测样本进行预测时,将b颗决策树预测值的均值作为最终预测结果。

图1 随机森林回归模型
2 基于PCA-RFR的故障定位方法
2.1 变量重要性度量测量因果关系系数
由于PCA模型下的统计量是对所有过程变量在相应空间变化信息的度量,从本质上说,所有过程变量对于统计量都存在因果关系。在预测模型下,通过去除变量x的作用,判断其对于预测输出变量y的影响程度即可得到该变量对于y的因果关系系数。
当对训练数据建立好随机森林回归模型后,变量重要性度量作为随机森林回归模型的一个属性,通过对OOB数据中输入变量x随机置换后(消除变量x信息影响)对于输出变量y预测精度的降低程度来衡量该输入变量对于输出变量的重要性。本文这里将其借以利用,将其作为输入变量对于输出变量的因果关系大小的度量。
对于变量重要性度量的计算主要分为以下4个部分:
1)对已建好的RFR模型f={h1,h2,...,hb},将oobi(i=1,2,...,b)数据带入相应的决策树进行预测,得到均方误差MSEi(i=1,2,..,b),均方误差的定义为:
(6)

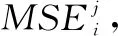
3)计算决策树hi(j=1,2,...,b)在变量xj随机置换前后的均方误差的差:
(7)
4)变量xj的变量重要性度量值:
(8)
SDNTE方法在计算变量间因果关系系数时需要对符号数、窗口大小等参数进行优化选择,同时需求大量样本建立概率统计模型,文献[12]中使用多达72 000组样本。相比较而言,变量重要性度量的计算就要简单容易的多,无需优化选择参数,随机森林回归模型一旦建好,即可得到变量重要性度量的数值,同时也能应用在少量样本场合,如对几百个样本便可建立良好的模型。由于随机森林回归通过并行构建决策树,这使得模型的构建也非常快速。
2.2 基于PCA-RFR的故障定位流程
PCA模型下的混合指标φ是对样本在主元和残差空间变化程度的度量,当发生故障时,φ统计量会增加并超过控制限,通过判断过程变量对于统计量指标φ的因果关系系数大小就可以进一步辨识出故障变量。
本文首先通过PCA模型筛选出发生故障的数据段,再将故障数据段的过程变量作为输入,对应的φ统计量作为输出建立RFR模型,最后通过模型的变量重要性度量系数值,系数值越大则表明该变量越有可能是引起φ统计量变化的变量,因此可将其辨识为故障变量。
基于PCA-RFR的因果分析故障定位流程如图2所示。具体步骤如下:
1)对工业过程的正常历史样本数据建立PCA模型,并得到统计量φ的控制限。
2)结合建立好的PCA模型和φ统计量控制限对离线采集数据进行故障检测,筛选出故障数据段并得到与其对应的φ统计量。
3)建立故障数据段的过程变量与φ统计量的RFR模型。
4)通过模型得到过程变量的变量重要性度量,对于变量重要性度量值最大的变量辨识为故障变量。

图2 基于随机森林回归的故障定位方法流程
3 仿真
3.1 数值仿真
参照文献[6]的数值仿真案例,其系统结构如式(9)所示:
(9)
其中:t1,t2和t3为均值为0,标准差分别为1,0.8,0.6的随机变量。噪声的均值为0,标准差为0.2。
通过对该仿真模型生成1000组正常样本并建立PCA模型。再通过对变量x3添加一个均值为0标准差为1的随机故障,生成1000组故障样本,建立该1000组故障样本变量数据与其φ统计量的随机森林回归模型,得到6个输入变量的变量重要性度量如图3所示,由图可知,PCA-RFR算法可以得到故障变量3的准确定位。

图3 数值仿真变量重要性度量
3.2 TE过程仿真
Tenessee Eastman(TE)过程是一个由纳西-伊斯曼公司公开的基于实际化工生产过程仿真系统,TE过程很好地模拟了实际复杂工业过程的主要特征,因此被广泛地应用于控制、优化、过程监控和故障诊断的研究中,其过程流程参见文献[17]。TE过程共有5个操作单元组成:反应器、分离器、循环压缩机、汽提塔和冷凝器。包含41个测量变量和12个控制变量,其中测量变量又分为22个过程测量变量和19个成分测量变量。TE过程有21种故障类型,包括阶跃、随机、缓慢漂移、阀粘滞等故障类型。
因为基于数据驱动的因果分析方法大多存在变量序列为平稳的限制,因此,本文采用22个连续过程测量变量进行研究,选择故障8-12共5种随机故障进行分析。正常和故障条件下的运行时间都为960个时刻,采样时间为3分钟,其中故障均从160时刻加入。
首先对正常数据建立PCA模型,选择故障条件下第161到960时刻共800个样本作为故障样本集,然后将故障样本集的过程变量作为输入,对应的φ统计量作为输出建立随机森林回归模型。随机森林回归算法在Sklearn机器学习库中决策树数量的默认参数为10颗,为了保证模型预测性能,这里将决策树数量参数选择为100颗。
故障11是反应器冷却水入口温度变化的随机故障,直接与之相关联的变量是变量x9(反应器温度)和变量x21(反应器冷却水出口温度)。基于GC、RBC、SDNTE以及PCA-RFR方法对故障11的故障定位结果分别如图4的(a)、(b)、(c)、(d)所示,其中GC因果分析方法首选通过筛选出故障候选变量集x3,x4,x5.x6,x8,x9,x14,x17,再通过变量间的因果关系指向识别出故障变量x9,但图中其余的孤立变量,无法判断其中是否存在故障变量。其余三种方法虽然同样都实现了故障变量x9的识别,但PCA-RFR对于变量x9的定位效果要明显更加突出。

图4 故障11的故障定位
故障12是冷凝器冷却水入口温度变化的随机故障,通过影响冷凝器对气体的冷凝效果直接影响到下游的变量x13(分离器压力变量)。基于GC、RBC、SDNTE以及PCA-RFR方法对故障11的故障定位结果分别如图5的(a)、(b)、(c)、(d)所示。其中GC方法定位出故障变量x12,筛选变量时遗漏了故障变量x13,基于RBC方法定位出故障变量x15,基于SDNTE方法定位出故障变量x22,而基于PCA-RFR方法定位出故障x13。因此,对于故障12仅有PCA-RFR实现了对故障变量的准确识别。
对于TE过程的5种随机故障,基于GC、RBC、SDNTE和PCA-RFR方法故障定位结果如表1所示。通过对比可以看出仅有PCA-RFR实现了对所有故障变量的准确识别。其在这5组故障中的定位效果要明显优于其他方法,验证了该方法的有效性和优越性。

表1 故障定位方法对比
4 结束语
提出了一种基于PCA-RFR的故障定位新方法,该方法利用变量重要性度量来衡量故障数据中过程变量对于φ统计量的因果关系大小,认定其中值越大的变量越有可能是故障变量。通过仿真实验验证了PCA-RFR方法在故障定位中的有效性。但该方法目前仅应用于离线数据故障定位中,基于随机森林回归模型的在线故障定位还有待进一步的研究。
