Investigation of the alloying effect on deformation behavior in Mg by Visco-Plastic Self-Consistent modeling

Alirez Mldr, Leyun Wng,∗, Goming Zhu, Xioqin Zeng,b,∗

aNational Engineering Research Center of Light Alloy Net Forming, School of Materials Science and Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

b The State Key Laboratory of Metal Matrix Composites, Shanghai Jiao Tong University, Shanghai 200240, China

Abstract Alloying elements can drastically alter the deformation behavior of Mg. In the present work, Visco-Plastic Self-Consistent (VPSC)modeling was employed to investigate the effect of alloying elements on Mg’s tensile behavior, in particular the relative activity of different slip and twinning modes. Mg-0.47wt.% Ca, Mg-2wt.% Nd, and AZ31 extruded alloys were deformed by micro-tensile tests in a scanning electron microscope (SEM). Texture and grain size measured by electron backscatter diffraction (EBSD) were used as the input for VPSC.After parameter optimization, the VPSC model successfully reproduced the stress-strain curve of each alloy. Simulation results indicate that the slip/twinning activity in the three alloys are different. Mg-0.47wt.% Ca shows strong extrusion texture, and prismatic slip was quite active during its tensile deformation. In contrast, Mg-2wt.% Nd shows weak extrusion texture, and basal slip was dominant. This alloy also developed more twinning activity than the other two alloys. AZ31 shows strong extrusion texture similar as Mg-0.47wt.% Ca, but prismatic slip was less active in it. The slip/twinning activity revealed by the VPSC model can explain the difference in the tensile behavior of the three alloys.

Keywords: Mg alloys; Crystal plasticity; Slip; EBSD; Tensile test.

1. Introduction

Mg and its alloys are characterized by high specific strength, good castability, and recyclability, making them promising structural material in a wide range of industries[1–3]. Yet, the formability of Mg still needs improvement.Theoretically, Mg can deform by basal slip, prismatic slip,pyramidal 〈a〉slip, and pyramidal 〈c+a〉slip. However, because the critical resolved shear stress (CRSS) of non-basal slips are much higher than that of basal slip, it is difficult to activate non-basal slips at room temperature, which limits Mg’s ductility [4].

Adding rare earth alloying elements can significantly enhance the ductility of Mg[5–7].Nd is frequently used for this purpose. While the ductility improvement has been traditionally attributed to the grain refinement and texture weakening effect by Nd [8–10], some studies also pointed out that Nd may promote non-basal slip in Mg [11,12]. Yet, the latter effect has not been quantitatively evaluated so far.

The high price of rare earth elements is a realistic obstacle for their usage. In recent years, Ca has received close attention as an alternative alloying element to improve Mg’s ductility [13–18]. Sandlöbes et al. [17] fabricated a Mg-1Al-0.1Ca (wt.%) alloy with ∼20% tensile elongation, and they attributed this phenomenon to the activation of 〈c+a〉slip by Ca solutes. Zhu et al. [18] conducted in situ tensile test for a Mg-0.47wt.% Ca specimen and studied the slip activity in hundreds of grains via slip trace analysis in a scanning electron microscope(SEM).While the majority of grains developed basal slip lines, prismatic and pyramidal 〈a〉slip lines were frequently identified in late deformation.The above two experimental works suggested that Ca is able to promote non-basal slip in Mg.

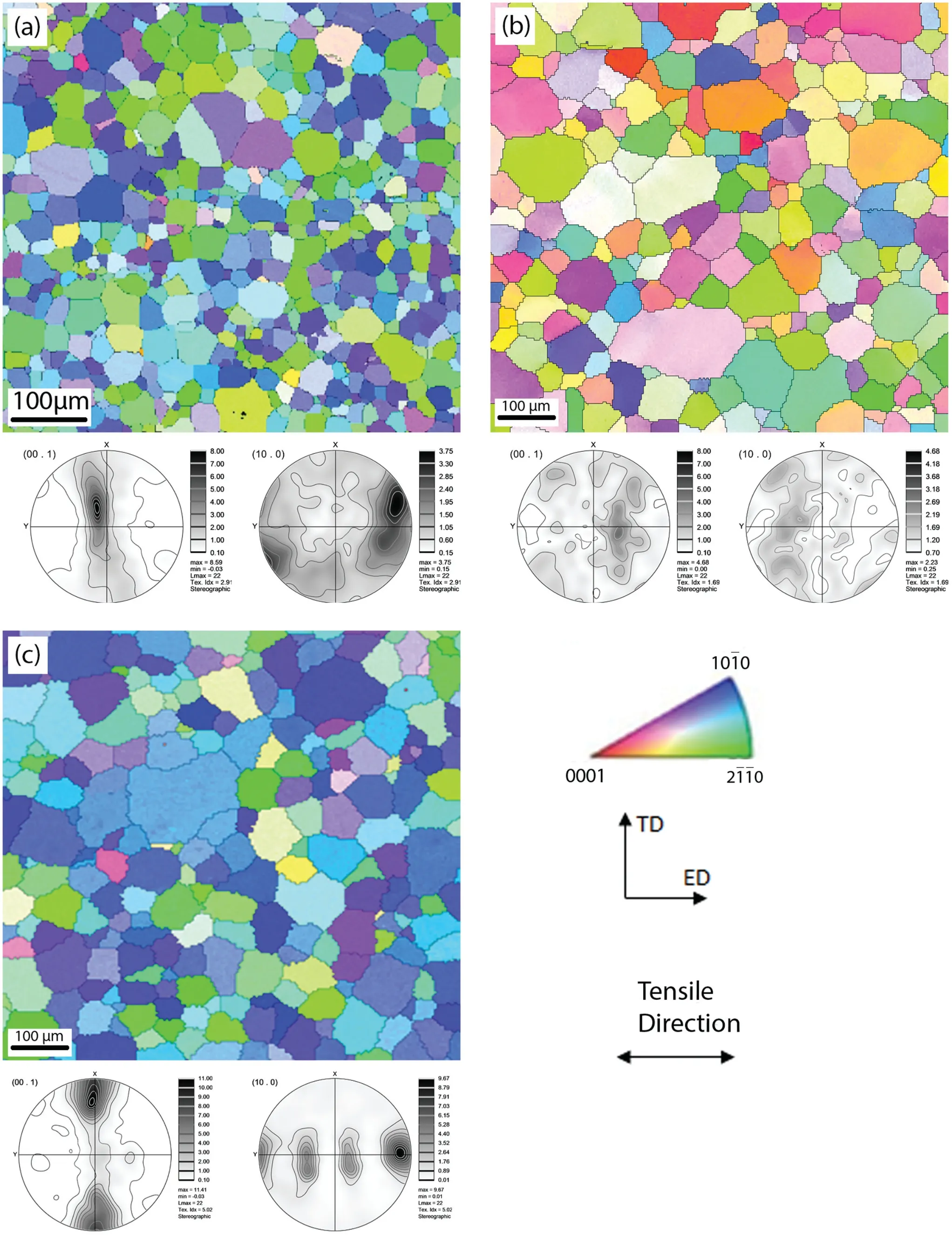
Fig. 1. Inverse pole figure maps and pole figures of the extruded (a) Mg-0.47wt.% Ca, (b) Mg-2wt.% Nd, and (c) AZ31 alloys. In each specimen, the tensile direction was parallel to the extrusion direction (ED).

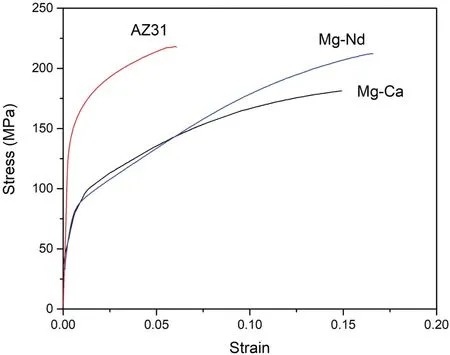
Fig. 2. Experimental stress-strain curves of the three alloys.

Table 1 Mechanical properties of the three alloys.

While SEM-based slip trace analysis [19–21] allows us to statistically study the activity of each slip mode, this method only examines slip activity in surface grains, which may not fully represent the bulk material behavior. Crystal plasticity simulation under the Visco-Plastic Self-Consistent (VPSC)framework can complement our understanding of the deformation details in bulk materials [22,23]. VPSC has been successfully applied to simulate the deformation behavior of various Mg alloys [24–26].

In the present work, VPSC is employed to simulate the tensile deformation of Mg–Ca,Mg–Nd,and AZ31 alloys.The goal is to understand how Ca and Nd affect the slip activity in Mg, which will provide a useful guideline for future alloy design.

2. Experimental and modeling procedures

2.1. Material and tensile test

Three different Mg alloys, Mg-0.47wt.% Ca, Mg-2wt.%Nd, and AZ31 were casted, homogenized, and hot extruded.In order to obtain similar grain sizes, the three alloys were extruded at 350 °C, 500 °C, and 350 °C, respectively, followed by annealing at 500 °C for 1h. The reduction ratio during extrusion was 18:1. Tensile specimens were fabricated from the as-extruded material by electron discharge machining into a flat dog-bone shape. The gage of each specimen is 11.0mm(L)×4.0mm(W)×1.4mm(T).The tensile direction is parallel to the extrusion direction. The top surface of each specimen was mechanically ground and electro-polished in an ethanol–10% perchloric acid electrolyte at 30V and −30°C for 150s for EBSD characterization.

Tensile tests were carried out by a MICROTEST 200N(Deben, UK) module placed in a Zeiss Gemini SEM with an EBSD system (Oxford Instrument, UK). Prior to the loading,an EBSD scan was conducted to record the initial microstructure of each alloy. The EBSD data was analyzed by OIMTMsoftware (EDAX Inc., USA). After that, tensile test was conducted at a constant crosshead speed of 0.1mm/min−1, which is equivalent to a nominal strain rate of 1.5×10−4/s.Each test was paused at 2% strain to capture texture evolution, then the test resumed until the specimen’s failure.

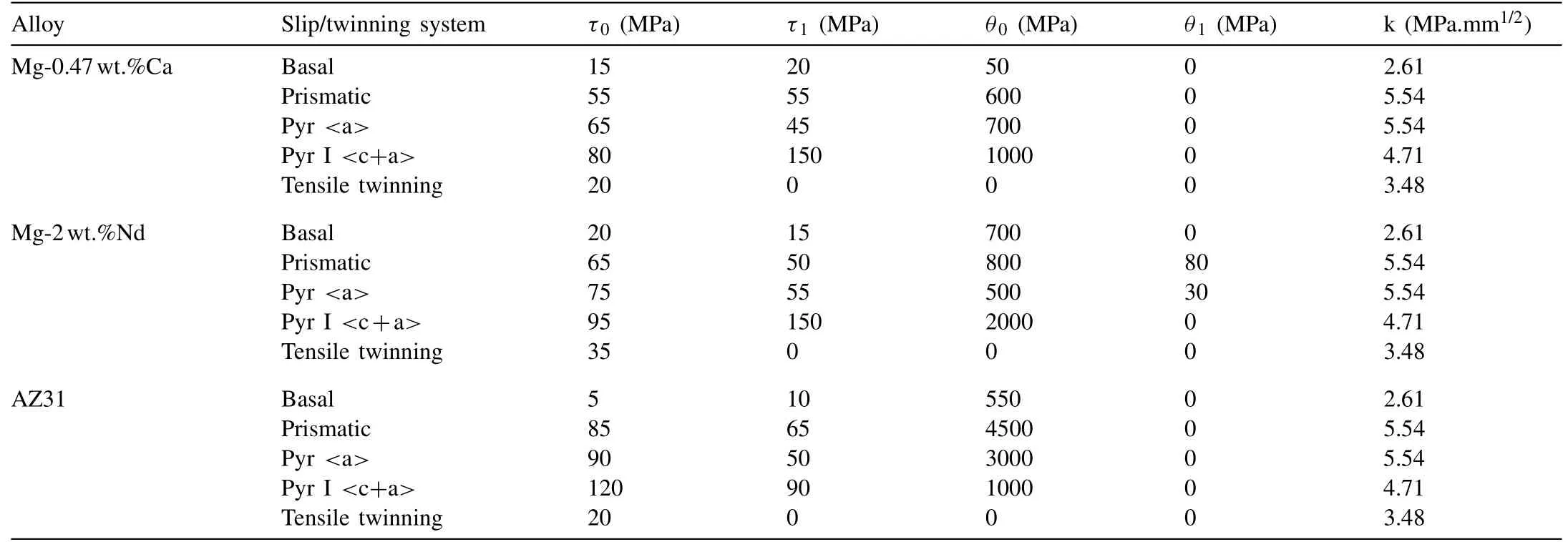
Table 2 Material parameters used in VPSC for the three alloys.

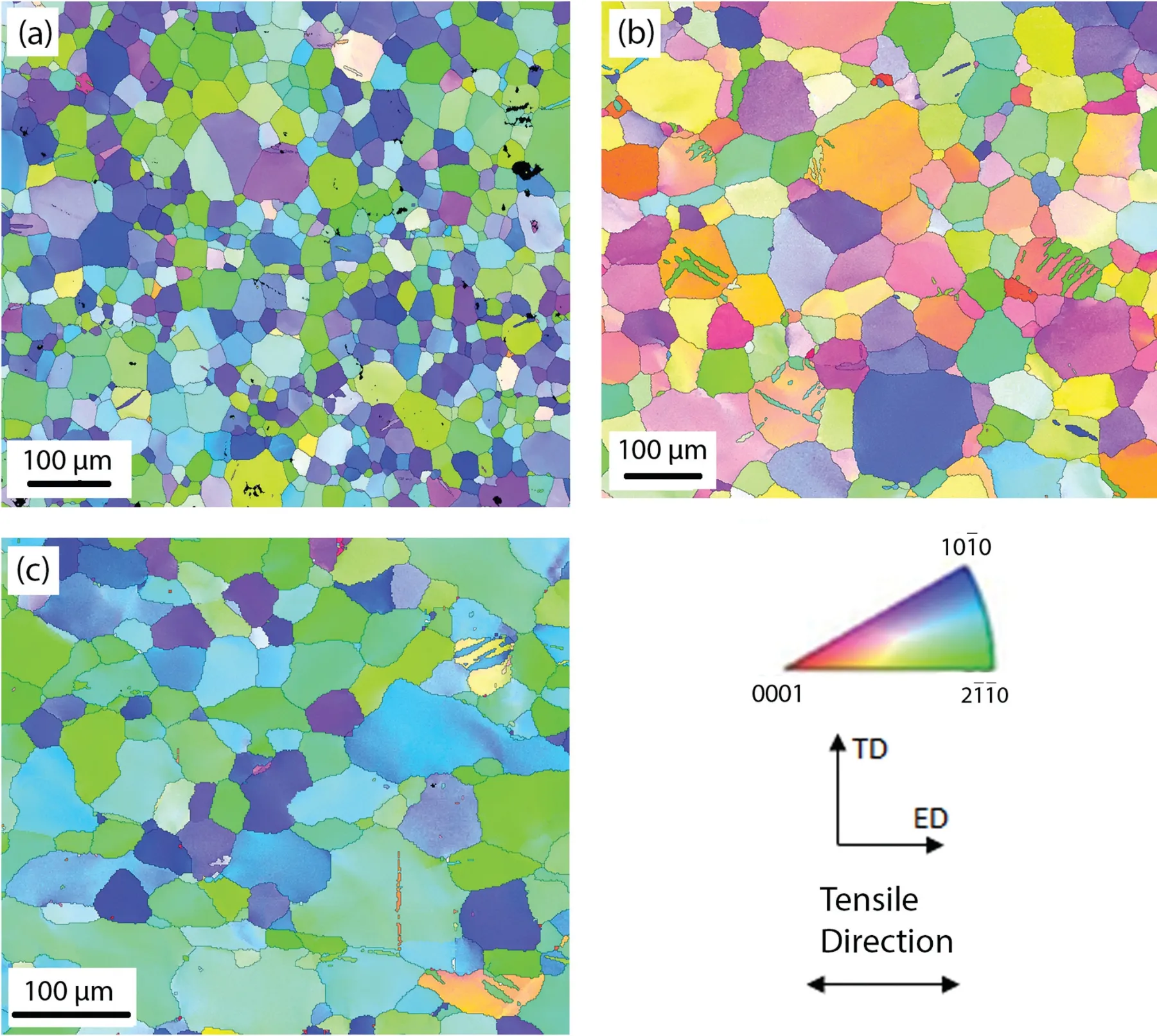
Fig. 3. IPF maps of the three specimens after 2% strain: (a) Mg-0.47wt.% Ca, (b) Mg-2wt.% Nd, and (c) AZ31.

2.2. VPSC modeling

VPSC was employed to simulate the tensile behavior of the three specimens. The VPSC framework was first developed by Lebensohn and Tomé [22,23,27,28], who used the self-consistent approach to describe the interaction between each grain and its local environment. In this framework, each grain is treated as an elastoplastic inclusion embedded within a Homogeneous Equivalent Medium (HEM). The grain has a specific orientation and volume fraction. More details about the VPSC homogenization scheme can be found in [29].

Deformation and texture evolution in each grain depends on the shear rates on all slip and twinning systems. The shear rate on a deformation system is determined by a rate sensitive criterion [29]:

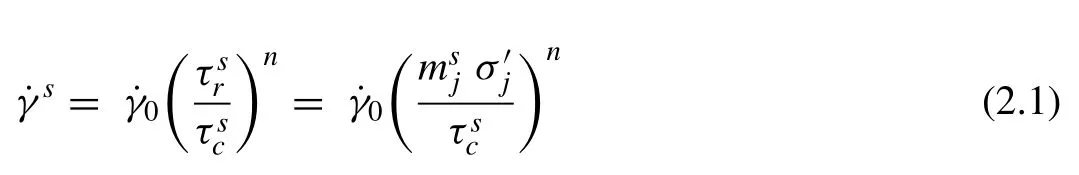
An extended Voce law describes the hardening behavior of each slip or twinning system. The shear resistance on system s after strainis given by [29]:

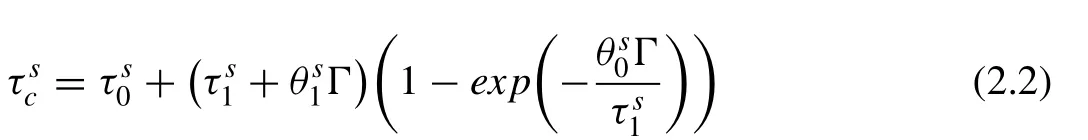
To address twin reorientation, the VPSC model adopts the Predominant Twin Reorientation (PTR) scheme [27]. PTR assumes that twinning is activated in a similar way as slip, but only along one direction. The code randomly picks a grain in each solving step to assess if the accumulated twin volume exceeds a threshold value. If so, the grain is reoriented to the twin orientation, and the volume of the reoriented grain is added to the “effective twinned volume”.

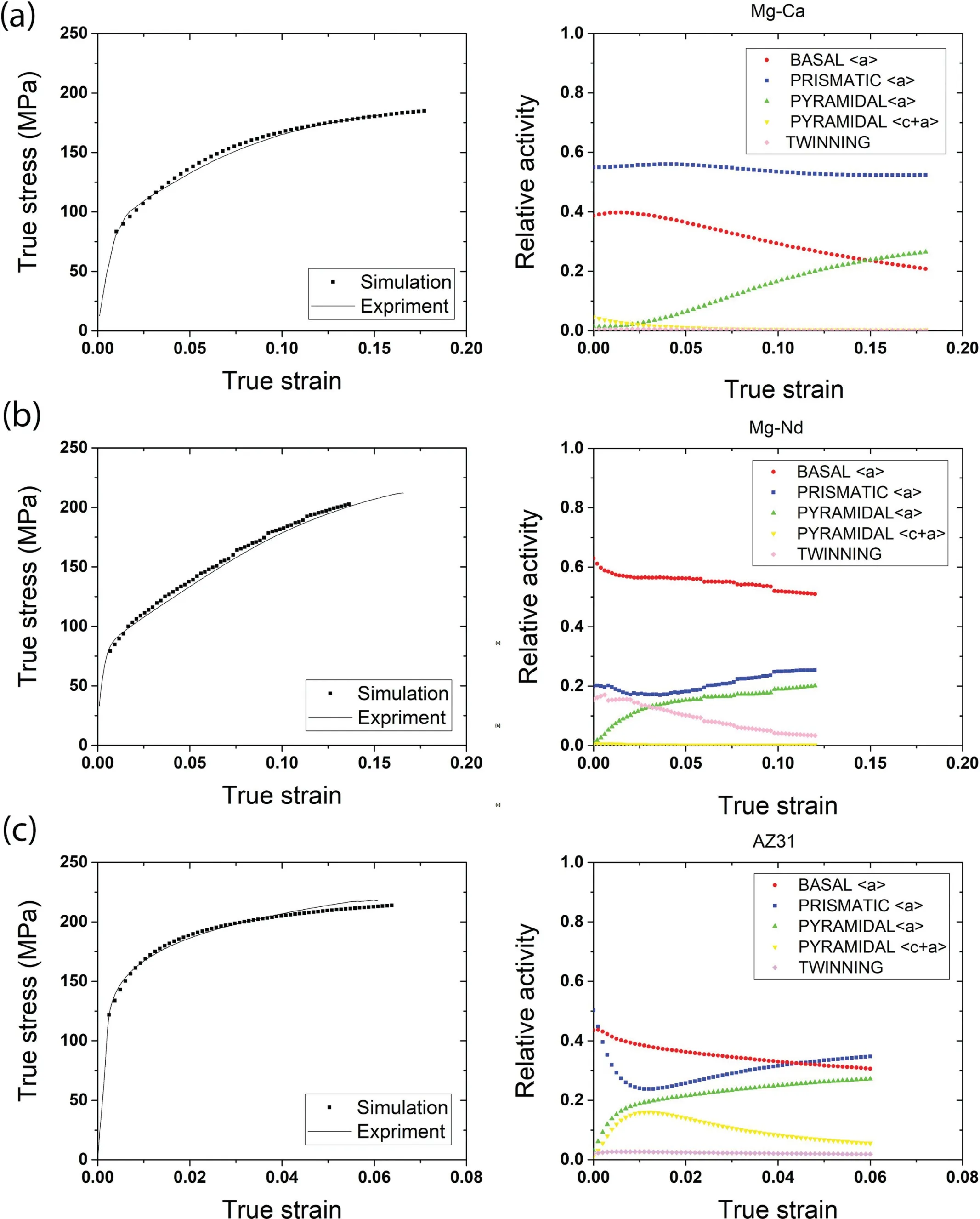
Fig. 4. Simulated stress-strain curves and relative activity of different deformation modes for (a) Mg-0.47wt.% Ca, (b) Mg-2wt.% Nd, and (c) AZ31.

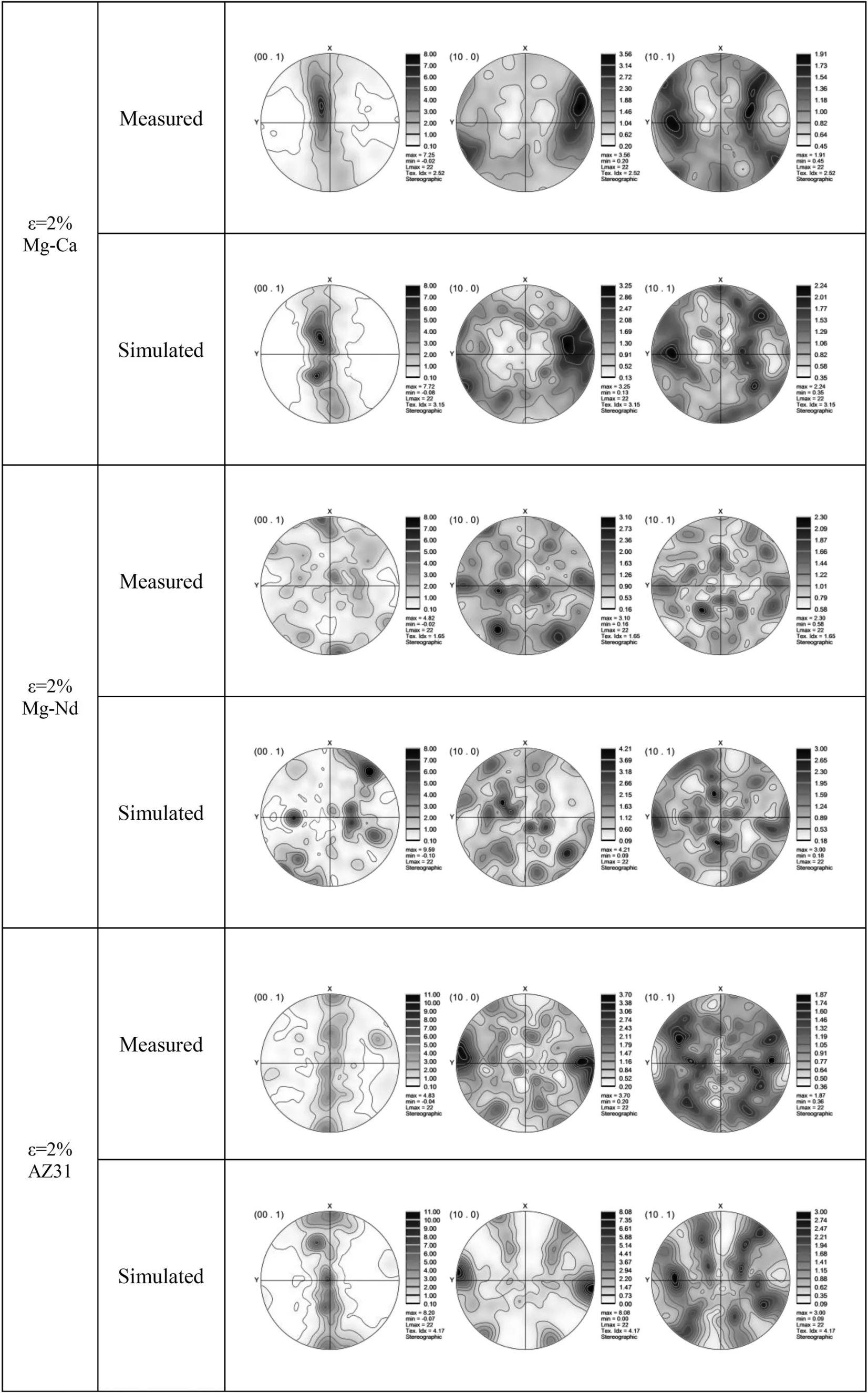
Fig. 5. Measured and simulated pole figures after 2% strain for (a) Mg-0.47wt.% Ca, (b) Mg-2wt.% Nd, and (c) AZ31.

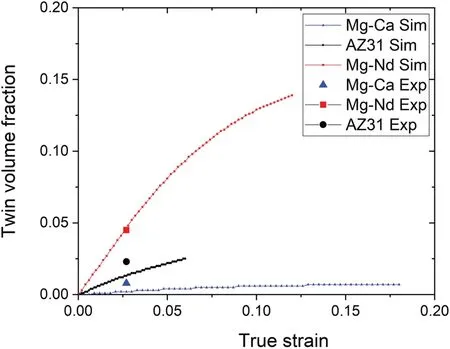
Fig. 6. Simulated twin volume fraction evolution as a function of strain for the three alloys. The measured values at 2% strain are also shown for comparison.

In this study, five deformation systems — basal, prismatic,pyramidal 〈a〉, pyramidal I 〈c+a〉and {10¯12}〈¯1011〉twinning— were taken into consideration. The VPSC model has the boundary condition of uni-axial tension along the load direction. Affine linearization scheme was selected to compute the relationship between the stress and average strain-rate in each grain. In addition, the model includes the Hall-Petch relationship that is available in the latest VPSC code. For each slip/twinning system, the Hall-Petch coefficient (k) follows the value in [30]. The texture of each specimen was calculated using the MTEX Matlab code based on the EBSD data,which serves as the input for VPSC [31].

3. Results

3.1. Experimental results

The initial microstructures of three different alloys are shown in Fig. 1 as inverse pole figure (IPF) maps and pole figures (PF). In all three alloys, the microstructure consisted of equiaxed, twin-free grains. The average grain diameter is about 35μm for Mg–Ca, and about 45μm for Mg–Nd and AZ31. Mg–Ca and AZ31 alloys exhibit typical extrusion texture, in which basal poles are nearly perpendicular to the extrusion direction. The Mg–Nd alloy shows more random distribution of the basal poles. This observation agrees with the literature [8,9] in that Nd can effectively randomize the wrought texture of Mg alloys.

The experimental stress-strain curves of the three alloys from the micro-tensile tests are illustrated in Fig. 2. Mechanical properties obtained from these stress-strain curves are summarized in Table 1. Tensile curves of Mg–Ca and Mg–Nd are similar, with Mg–Nd having slightly lower yield strength but higher elongation than Mg–Ca. In contrast, the tensile curve of AZ31 is significantly different:it shows much higher yield strength but much lower elongation.

IPF maps of the three specimens after 2% tensile strain were measured by EBSD again and shown in Fig. 3. Twin volume fraction in the Mg–Nd specimen with weak texture is apparently higher than the other two specimens with stronger texture.

3.2. Modeling results

The material parameters used in VPSC for the three alloys are shown in Table 2, including τ0, τ1, θ0, θ1, and k (Hall-Petch coefficient). The simulated stress-strain curves using these parameters closely match the experimental stressstrain curves, as illustrated in Fig. 4. It should be noted that the VPSC model does not consider elastic deformation, so the elastic strain was separately computed using the elastic modulus of Mg (45GPa).

Deformation often leads to texture changes. The experimentally measured and VPSC predicted textures after 2% deformation are compared to each other in Fig. 5 for the three alloys. For all three alloys, the pole figures from simulation generally match the experimental results.

Fig. 6 displays the simulated twin volume fraction evolution as a function of strain. The twin volume fraction at 2%strain is compared with the EBSD measurement. For Mg–Nd,the predicted twin volume fraction nearly equals the measured value (∼5%). For Mg–Ca and AZ31, the model underestimated the twin volume fraction. In VPSC, the criterion for twin nucleation is similar as the activation of dislocation slip: when the resolved shear stress on the twinning system exceeds a threshold value, the twin will nucleate. However,this criterion neglects the effect of local stress concentration and/or strain transfer across grain boundaries that can lead to twin nucleation even when the parent grain has an unfavorable orientation [32,33]. Mg–Ca and AZ31 have typical extrusion texture that is unfavorable for twinning; the observed twins were likely caused by stress concentration and strain transfer.This is probably why the VPSC model underestimated the twin volume fraction in these two alloys.

4. Discussion

The tensile stress-strain curves of Mg–Ca and Mg–Nd are nearly identical, despite the fact that they exhibit very different initial textures. AZ31, on the other hand, shows much higher yield strength but much lower elongation. This can be understood from the relative activity of different deformation modes in Fig 4. According to the VPSC simulation result, in Mg–Ca, prismatic slip was quite active during its deformation (Fig 4(a)). After 5% strain, pyramidal 〈a〉slip increased rapidly.Therefore,the high ductility in Mg–Ca is attributed to the active non-basal 〈a〉slip. Tensile twinning and pyramidal〈c+a〉made little contribution for the plastic deformation.These findings from VPSC are consistent with experimental observations of surface slip traces in this alloy [18]. In Mg–Nd, because of the weak texture, basal slip was the dominate slip mode and twinning was also active (Fig 4(b)). The high ductility in Mg–Nd is mainly attributed to the texture effect.In AZ31, neither basal slip nor non-basal 〈a〉slip could be easily activated. Pyramidal 〈c+a〉slip was notably active.The high strain hardening in AZ31 could be caused by the interaction between 〈a〉and 〈c+a〉dislocations.

From the material parameters in Table 2, we can also infer how different alloying elements influence the CRSS values of different slip modes in Mg.The CRSS ratio between prismatic and basal slip (CRSSprism/CRSSbasal) in Mg-0.47wt.% Ca and Mg-2wt.% Nd are 3.7 and 3.3 respectively. These values are lower than that in pure Mg (5–50) [34,35] and AZ31 (4.5–30)[36,37]. When the CRSSprism/CRSSbasalratio is low, prismatic slip is easy to be activated, which enhances the ductility of the material.This explains why Mg–Ca and Mg–Nd are much more ductile than AZ31. Future alloy design should take the CRSSprism/CRSSbasalratio into account.

5. Conclusions

VPSC modeling was conducted to study the tensile deformation behavior in three extruded Mg alloys: Mg-0.47wt.%Ca, Mg-2wt.% Nd, and AZ31. The main conclusions are as follows:

(1) Mg–Ca and Mg–Nd show similar tensile stress-strain curve; AZ31 has higher yield strength but less elongation to failure. The macroscopic stress-strain curves of the three alloys are successfully reproduced by the VPSC model using different material parameters.

(2) In Mg–Ca, prismatic slip is the most active slip mode.Pyramidal 〈a〉slip increased rapidly in late deformation.Ca reduces the CRSSprism/CRSSbasalratio. Activity of non-basal 〈a〉slip is the main reason for the enhanced ductility in Mg–Ca.

(3) In Mg–Nd, the extrusion texture is much weaker than the other two alloys, so that basal slip is the dominant slip mode and twinning is also active. The enhanced ductility in Mg–Nd is mainly attributed to the weak texture. Nd also reduces the CRSSprism/CRSSbasalratio.

(4) In AZ31, the extrusion texture is strong and the CRSSprism/CRSSbasalratio is high. As a result, it has a relatively low tensile ductility compared to Mg–Ca and Mg–Nd.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

The authors gratefully acknowledge the financial support of the projects from the National Natural Science Foundation of China (Nos. 51631006, 51671127, 51825101). We also thank Dr. Carlos Tomé for the help in using the VPSC code.