Formulation of corrosion rate of magnesium alloys using microstructural parameters

Ahmad Bahmani, Srinivasan Arthanari, Kwang Seon Shin

Magnesium Technology Innovation Center, School of Materials Science and Engineering, Seoul National University, 1 Gwanak-ro, Gwanak-gu, Seoul 08826,Korea

Abstract Up to the date of writing this article, a quantitative analysis between corrosion rate and combined microstructural parameters including composition, grain size, and precipitations has not been reported. Hence, a literature review was carried out on these parameters to understand the quantitative effect of each one on the corrosion rate of Mg and Mg alloys. Moreover, using the available data in the literature and several experimental results, a new model was developed to predict the corrosion rate, through microstructural parameters. This model suggests that by using ultra-fined grains, alloying compounds with low Volta-potential difference relative to the matrix and a low fraction of secondary phase, a very low corrosion rates of materials are achievable.

Keywords: Corrosion rate; Magnesium; Grain size; Volta-potential.

1. Introduction

The corrosion rate is the rate of corrosion attack to material and is the most straightforward parameter to compare the corrosion behavior of materials. Prediction of the corrosion rate by considering several microstructural parameters of material is still a challenging task. Indeed, several parameters such as intrinsic/extrinsic microstructural parameters and alloying produce complex mechanisms involved in corrosion.Even though the corrosion rate determines the life of components in use and it is one of the most critical parameters in industry, to our knowledge, a relationship between corrosion rate and some affecting microstructural parameters using a model equation have not been previously reported.

Throughout the history of the industry, engineers have always been involved in designing new materials with desired properties. The corrosion rate is one of those properties that limit the application of materials. Magnesium alloys are the most challenging materials because they are very attractive in the industry due to their high strength to weight ratio which makes the components lighter, however, their high corrosion rate restricts their usage. Having the ability to predict the corrosion rates can help researchers and engineers to design the material with the desired corrosion rate without altering much on the mechanical properties. They may also find out the routes of designing stainless magnesium which is very important in large scale applications.

Therefore, in this work, we propose an equation considering how the microstructural parameters can model the corrosion rate. Even though the model has been defined for the magnesium alloys and all studied works have been done in magnesium alloys, but same work can be extended on other alloys and the equation can be generalized for other materials as well.

1.1. Parameters influencing the corrosion behavior

There are several parameters such as composition, grain size (grain boundary), and second phase which mainly determine the corrosion rate of Mg alloys.

1.1.1. Alloy composition

The alloy composition has two effects on the corrosion rate such as intrinsic and extrinsic:

1.1.1.1. Intrinsic effect.

- Surface potential: Surface potential (surface nobility or weakness) of the matrix can be changed by the dissolution of solutes into the matrix [1]. Further, the surface potential might also be changed by lattice strain (dislocation density), which is related to the deformation conditions.A linear relationship exists between the surface potential and work function which is the minimum energy required to remove an electron from the surface of a material to a point in a vacuum outside the surface. Surface potential can be measured by various techniques such as scanning kelvin probe force microscopy (SKPFM) which is commonly used for several alloys [2,3]. Open circuit potential(OCP) can also be used; however, OCP includes other effects such as grain boundary and second phases. The first principle calculation has also been utilized to measure the work function of the surface [4].

- Second phases:The addition of alloying elements produces second phases with different fractions. (This effect will be discussed later).

- Orientation (Texture Effect): Here the effect of texture has also been considered as their effect on metal matrix.The corrosion rate of a metal matrix with various crystalline orientations could be affected by changes in alloying composition (CRT,C). It is known that the different crystallographic orientations have different corrosion rates. For directionally deformed alloys with intense texture, this parameter needs to be considered. The corrosion rate related to the effect of orientation can be considered as aC×(∑fA,or×CRor), where aCis the effect of solutes and density of dislocations in altering the corrosion rate of grains, and fA,orand CRorare the area fraction of each orientation and corrosion rate of the related orientation, respectively. Several studies have been carried out to understand the effect of texture on the corrosion rate.In fact, since different crystallographic planes have different atomic densities, they show different corrosion rates.In HCP-structured materials, basal planes and after that prismatic II and then prismatic I planes have the highest corrosion resistance compared to other intermediate planes[5–13]. Additionally, it has been reported that any misorientation from the packed planes including basal and prismatic planes increases the corrosion rate [6].

So, it can be seen that the effect of the composition can be considered through a few parameters which affect microstructure, second phase distribution, and their potential difference,or altering the possible passive layer formation.

1.1.1.2. Extrinsic effect (Passivation: CRP,C). Passivation is the formation of an outer layer such as metal oxide on the base metal as a micro coating through the chemical reaction of base material with the aqueous environment/electrolyte and it protects the substrate against further corrosion. Passivity in an Mg alloy is achieved by enough concentration of elements such as Ca, Y or Al having the passivating capability in the matrix [14]. Passivation is related to several parameters such as formation Gibbs free energy (or enthalpy in a fixed temperature), cohesive energy which shows overall chemical stability of a material [15], Pilling-Bedworth (PB) ratio which shows the compactness and also coherency of the layer with the substrate. A higher Ecohimplies that more energy is required to break up the primary chemical bonds. For instance Y, Al and Ca hydroxides have higher cohesive energy than Mg(OH)2, and they can significantly improve the corrosion resistance of alloys [15]. The PB ratio of MgO on the surface is less than 1 (PB < 1) resulting in weak coverage of the surface or forming a porous film [16]. In fact, high-purity Mg is active in all experimental conditions except in chromic acid solution [17,18]. Even though some elements such as Ti,Al and Cr may form oxide films with PB ratio >1, but their oxides have high solubility in aqueous solutions. Hence, they cannot usually produce a stable and protective surface film on Mg [14].

1.1.2. Grain size

Grain size is an important factor that determines mechanical properties and corrosion behavior of metals. In the case of mechanical properties, yield strength and hardness are related the grain size through the Hall-Petch equation. However, the effect of grain size on the corrosion rate is more complicated and there are several controversial reports where some reported increase in grain size increases the corrosion rate and some report the opposite.

In order to understand the effect of grain size on the corrosion rate, a literature review was done for various pure metals as well as alloys which are summarized in Table 1. From Table 1, it can be concluded that different relationships and trends between grain size and corrosion rate for both pure materials and alloys can be noticed. Based on the literature,the relationship between grain size and corrosion rate can be classified as:

(i) Increase in grain size decreases the corrosion rate. The reasons could be:

- Decreasing lattice strain and dislocations density and decreasing the surface potential (at elevated temperatures)

- Dissolution of second phases into the matrix at elevated temperatures (as a side effect during the heat treatment)

- Continuous cathodic second phases formed in the casting of alloys (especially with a high concentration of alloying elements and second phase) may break down into several isolated phases within deformation and their role as protection might be changed to several isolated cathodic cells that accelerate the dissolution of the matrix.

(ii) Decrease in grain size decreases the corrosion rate:

Ref.[24][25][23][27,28[29][20][30][32][33](continued on next page)The mechanism Preferred crystallographic pitting (PCP) was initiated by Fe precipitates in pure Mg and was propagated along with a(0 0 0 1) plane in a grain. Refining the grain size of pure Mg by hot extrusion reduced PCP propagation, indicating that the grain boundaries act as a barrier to pit propagation The film resistance of the pure magnesium sample extruded at 250°C was the lowest, and the result indicates that magnesium hydroxide film formed on the surface of the sample extruded at higher temperature is thinner or less stable, so that the electrolyte can easier penetrate and promote the continuous dissolution of the pure magnesium Decreasing the corrosion rate at higher solidification rate was attributed to refined grains that can produce more uniform and dense films on the surface of pure magnesium Increasing the intensity of basal planes by increasing the number of passes enhances the corrosion resistance and hence decreases the corrosion rate Grain refinement resulted in larger lattice strain and defects and hence deeper pits and higher corrosion rate Increased number density coupled with high misorientated grain boundaries after ECAP promoted a more coherent hydroxide layer on the surface ECAP introduces several dislocations and lattice defects. A MgO/Mg(HO)2 passive film is probably nucleated on these defects. Introducing more defects by ECAP leads to nucleation of more sites for the formation of film on the substrate The corrosion rate decrease after grain refinement is due to rapid passivation of UFG Ti and segregation of impurities on grain boundaries Johansen et al. [31] found that the Ti oxide film formed faster on the surface of 34% plastically deformed samples than that of annealed ones Lower passivation current was found for deformed Ti than for annealed Ti in Tomashov and Ivanov’s research [32].They believed that passivation first started on lattice defects at the exposed surface.UFG Ti has a high density of grain boundaries and dislocations inside grains leading to a high fraction of passive sites and hence, low corrosion rate The main reason for improved corrosion resistance of BNII(Bulk Nano Crystalline Iron Ingot) comparing with CPII(Poly Crystalline Iron Ingot) may be related to the difference between their microstructure and texture. The orientation〈111〉(110) was dominant and this texture has been enhanced after rolling. Moreover, dislocations in the rolled surface for BNII are less than CPII, resulting in a decrease of corrosion How to change D Extrusion of cast material(250°C)Temp. (180,220, 250°C)Solidification Rate Number of passes Number of passes Number of passes ECAP Temp.ECAPed material was annealed at 80 °C Severe rolling CR ?D decreases ➔Decreases Decreases Decreases Decreases Increases Decreases Increases (with decreasing processing temperature from 360 to 250°C) and increases (with decreasing processing temperature from 250°C to 200°C)Decreases Decreases Hank’s Solution 3.5wt.% NaCl A literature review on the effect of grain size on corrosion rate.SBF [26]SBF 3.5wt.% NaCl 0.1M NaCl SBF HCL-H2SO4(1, 3 and 5M)Na2SO4 Material Pure Mg Pure Mg Pure Mg Pure Mg Pure Mg Pure Mg Pure Mg Pure Ti Pure Fe Process Extrusion Extrusion Directional Solidification FSP ECAP from Cast ECAP ECAP ECAP and Anneal Severe Rolling Table 1 Grain size, D(μm)6000– 30 30–20 1000–200 1000–11.5 1500–200 100–2 1500–9 7.0–0.3 N/A

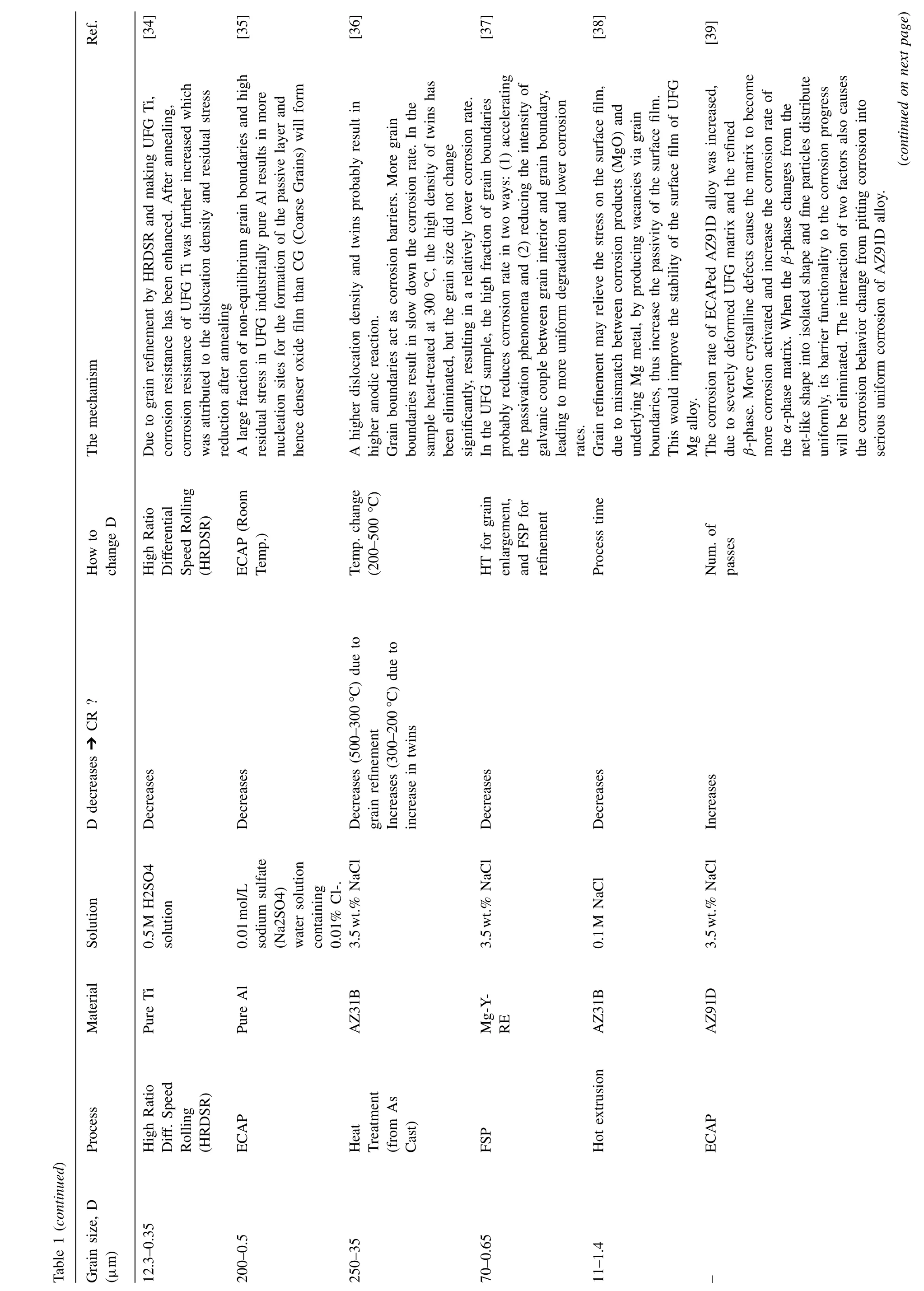
Ref.The mechanism How to change D CR ?D decreases ➔SolutionMaterial Table 1 (continued)Process Grain size, D(μm)[34][35][36][37][38][39]Due to grain refinement by HRDSR and making UFG Ti,corrosion resistance has been enhanced. After annealing,corrosion resistance of UFG Ti was further increased which was attributed to the dislocation density and residual stress(continued on next page)reduction after annealing A large fraction of non-equilibrium grain boundaries and high residual stress in UFG industrially pure Al results in more nucleation sites for the formation of the passive layer and hence denser oxide film than CG (Coarse Grains) will form A higher dislocation density and twins probably result in higher anodic reaction.Grain boundaries act as corrosion barriers. More grain boundaries result in slow down the corrosion rate. In the sample heat-treated at 300 °C, the high density of twins has been eliminated, but the grain size did not change significantly, resulting in a relatively lower corrosion rate.In the UFG sample, the high fraction of grain boundaries probably reduces corrosion rate in two ways: (1) accelerating the passivation phenomena and (2) reducing the intensity of galvanic couple between grain interior and grain boundary,leading to more uniform degradation and lower corrosion rates.Grain refinement may relieve the stress on the surface film,due to mismatch between corrosion products (MgO) and underlying Mg metal, by producing vacancies via grain boundaries, thus increase the passivity of the surface film.This would improve the stability of the surface film of UFG Mg alloy.The corrosion rate of ECAPed AZ91D alloy was increased,due to severely deformed UFG matrix and the refined β-phase. More crystalline defects cause the matrix to become more corrosion activated and increase the corrosion rate of the α-phase matrix. When the β-phase changes from the net-like shape into isolated shape and fine particles distribute uniformly, its barrier functionality to the corrosion progress will be eliminated. The interaction of two factors also causes the corrosion behavior change from pitting corrosion into serious uniform corrosion of AZ91D alloy.High Ratio Differential Speed Rolling(HRDSR)ECAP (Room Temp.)Temp. change(200–500 °C)HT for grain enlargement,and FSP for refinement Process time Num. of passes Decreases Decreases Decreases (500–300°C) due to grain refinement Increases (300–200°C) due to increase in twins Decreases Decreases Increases 0.5M H2SO4 solution 0.01mol/L sodium sulfate(Na2SO4)water solution containing 0.01% Cl-.3.5wt.% NaCl 3.5wt.% NaCl 0.1M NaCl 3.5wt.% NaCl Pure Ti Pure Al AZ31B Mg-YRE AZ31B AZ91D High Ratio Diff. Speed Rolling(HRDSR)ECAP Heat Treatment(from As Cast)FSP Hot extrusion ECAP 12.3–0.35 200–0.5 250–35 70–0.65 11–1.4–

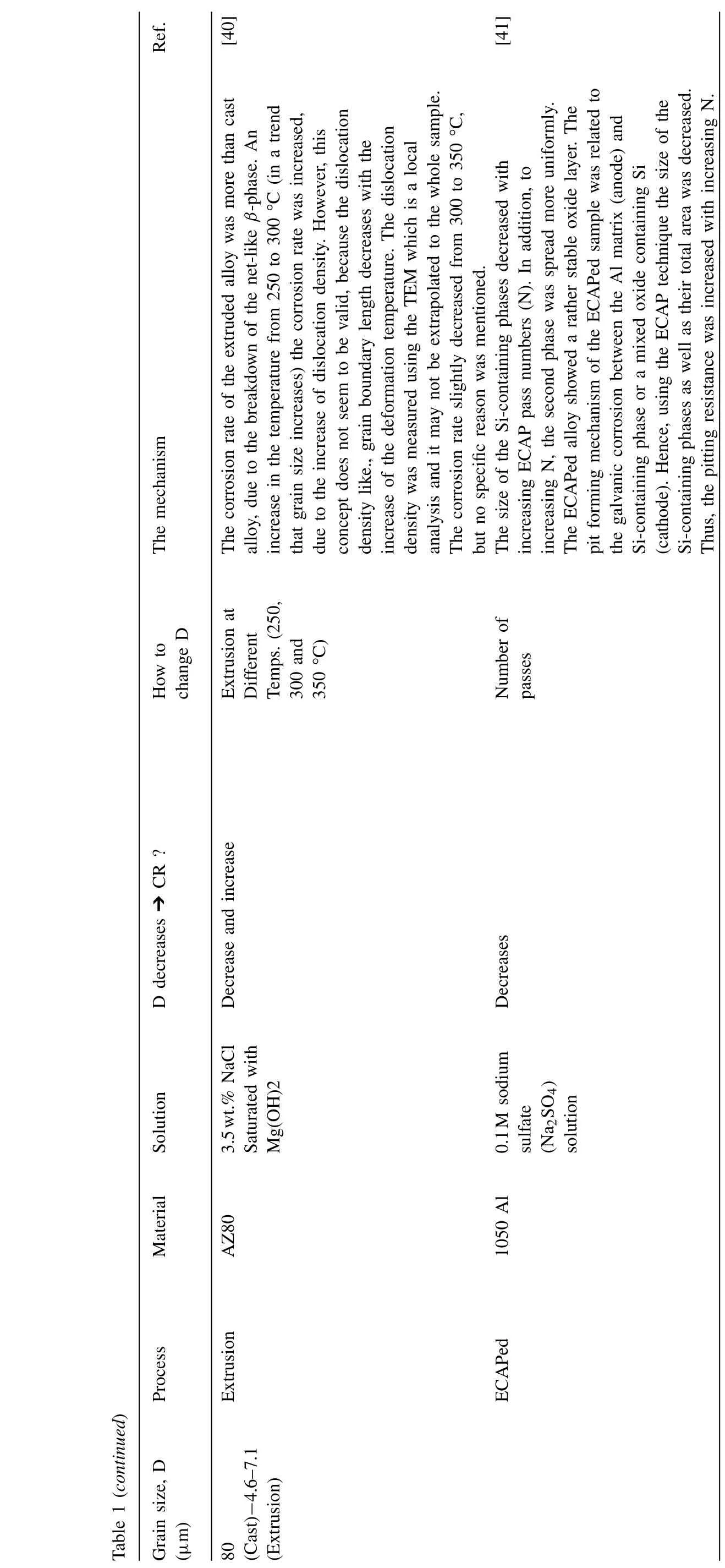
Ref.The mechanism How to change D CR ?D decreases ➔SolutionMaterial Table 1 (continued)Process Grain size, D(μm)[40][41]The corrosion rate of the extruded alloy was more than cast alloy, due to the breakdown of the net-like β-phase. An increase in the temperature from 250 to 300 °C (in a trend that grain size increases) the corrosion rate was increased,due to the increase of dislocation density. However, this concept does not seem to be valid, because the dislocation density like., grain boundary length decreases with the increase of the deformation temperature. The dislocation density was measured using the TEM which is a local analysis and it may not be extrapolated to the whole sample.The corrosion rate slightly decreased from 300 to 350 °C,but no specific reason was mentioned.The size of the Si-containing phases decreased with increasing ECAP pass numbers (N). In addition, to increasing N, the second phase was spread more uniformly.The ECAPed alloy showed a rather stable oxide layer. The pit forming mechanism of the ECAPed sample was related to the galvanic corrosion between the Al matrix (anode) and Si-containing phase or a mixed oxide containing Si(cathode). Hence, using the ECAP technique the size of the Si-containing phases as well as their total area was decreased.Thus, the pitting resistance was increased with increasing N.Extrusion at Different Temps. (250,300 and 350 °C)Number of passes Decrease and increase Decreases 3.5wt.% NaCl Saturated with Mg(OH)2 0.1M sodium sulfate(Na2SO4)solution AZ80 1050 Al Extrusion ECAPed 80(Cast)−4.6–7.1(Extrusion)

- Enhancement of a more uniform and coherent passivation layer by grain refinement.

- More grain boundaries act as more barriers against preferred crystallographic pitting (PCP)

- Enhancement the basal plane intensity (as a side effect of grain refinement depending on the deformation processes)

It is clear from the reports that the type of alloy, distribution of second phases, processing routes for changing the grain size, and electrolyte type result in different trends. In order to understand the real effect of the grain size on the corrosion behavior, we have classified these studies into two major groups including pure metals and alloys.

Fig. 1 shows the results of electrochemical study including open circuit potential (OCP) and electrochemical impedance spectroscopy (EIS) of pure Mg extruded at 260°C followed by multi -directional forging (MDF) at various temperatures(220, 260, 300 and 340 °C) in 3.5wt.% NaCl saturated with Mg(OH)2solution. The details of this experiment have been mentioned elsewhere [19]. The OCP values from the initial 0.5h(Fig.1(a))and after 24h(Fig.1(b))shows that corrosion products that form on the surface of all the samples gradually shifted the surface potential to the nobler direction. The potential has a direct relationship with the grain size.Since grain boundaries have a lower potential than the matrix, OCP shifts to lower values. The EIS Nyquist plots of the 0.5h immersed samples depict that MDF at lower temperatures improved the corrosion resistance of pure Mg. The increase in diameter of the semi-circle of the MDF220 sample clearly shows that material with smaller grain size has more ability to acquire the passivity behavior, due to the more coherent and stable passive layer formed on the exposed surface of the metal with more grain boundaries. In fact, grain boundaries, by providing more dislocations, compensate the mismatch of the hydroxide/oxide layer with the base metal [20–23]. Changing the grain size by changing process conditions such as temperature, number of process passes, the direction of applying deformation, and casting cooling rate will also change the second phase distribution and matrix concentration, so these effects also need to be considered in corrosion behavior of alloys.

Fig. 2 depicts the corrosion rate vs grain size of pure Mg obtained from different studies. It seems that even in the pure Mg, the single trend in corrosion rate vs grain size was not noticed. While in some cases, corrosion rate increases with increasing the grain size, in others it decreases. As a matter of fact, grain boundaries are the high energy sites and so,corrosion initiates from these sites. With an assumption of no defect in the material, grain boundaries should increase the corrosion rate. That is why a single crystal material with the packed orientation like basal plane exposed to the corrosion has a very low corrosion rate (∼0.5mm/y in simulated body fluid (SBF) for 1d immersion) [8]. But adding grain boundaries and decreasing the grain size, increases the corrosion rate by localizing the corrosion and breaking down the surface layer.However,in the majority of the cases,the corrosion rate has been decreased by decreasing the grain size.

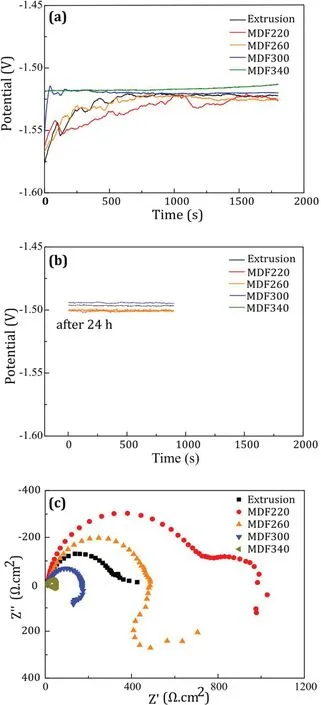
Fig. 1. The electrochemical study results of extruded and MDF pure Mg(a) OCP within 0.5h immersion, (b) OCP after 24h and (c) EIS after 0.5h immersion [19].

So it can be concluded that in the case of single grains like single crystals or bi-crystals, corrosion rate increases with increasing the grain size, while in very fine grains (maybe less than 50μm in) corrosion rate decreases by decreasing the grain size. However, the possibility of passivation due to the solution property should be considered. Less aggressive solutions like 0.1M NaCl will probably increase the range of passivation, so the grain size tolerance to provide the passivating layer increases (Fig. 3).

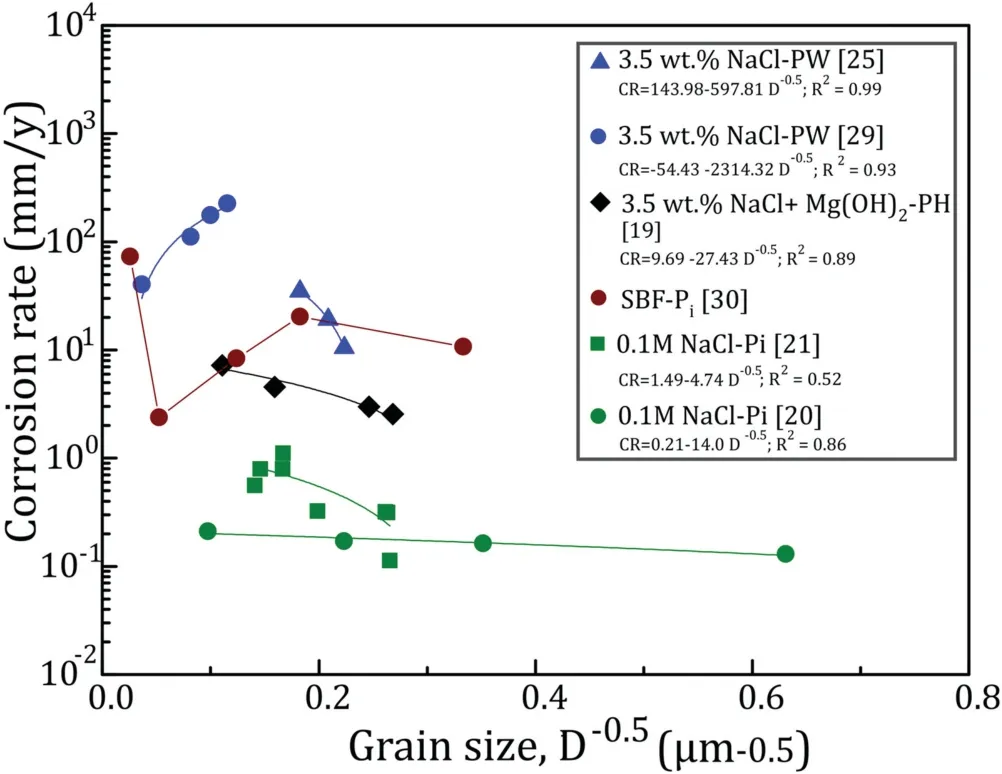
Fig.2. Effect of grain size on the corrosion rate of pure Mg[19–21,25,29,30](Pi, Pw and PH are corrosion rate measured by polarization, weight loss and hydrogen evolution methods, respectively).

To formulate the effect of grain size on the corrosion rate we may use the Hall-Petch type equation that was proposed by Ralston et al. [21]. The corrosion rate is related to the grain boundary length (GBL) and GBL is linearly related to D−0.5, where D is the grain size. Therefore the corrosion rate(CR) can be written as follows:

Where a, and b are the fitting constants related to other parameters which will be discussed later. Since grain size effect should be applied just on the matrix, a surface fraction of matrix,fA,m(=1-∑fA,i),was multiplied by the term D.Therefore the equation could be changed as:

As explained, the grain size may have effects in two different ways [20, 21,35,42], so the grain size-related corrosion can be written as:

(1) −b1×fA,m×D−0.5for small grains or solutions providing passivation. “-” depicts that corrosion rate increases with increasing grain size [20, 21,43,44]

(2) +b2×fA,m×D−0.5for very large grains including single- or bi-crystals or in solutions where passivation is not possible. “+” shows that the corrosion rate decreases with increasing grain size [30,35,42].

One of the most effective ways to achieve ultra-fine grains are using severe plastic deformation, where not only yield strength can be effectively improved, but also, the corrosion rate can be decreased [45]. Several SPD techniques such as equal channel angular pressing/extrusion (ECAP/ECAE) [46–51], high ration differential speed rolling (HRDSR) [52–54],accumulative roll bonding (ARB) [55–58], accumulative back extrusion(ABE)[59–63],three roll planetary milling or screw rolling (SR) [64–66], friction stir welding (FSW) [67–70],high pressure torsion [71–74] and multi-directional forging(MDF) [75–84] have been reported. Using these techniques or any other process like powder metallurgy, it is possible to achieve UFG or even nano-grains.

1.1.3. Second phase (phase fraction and volta-potential)

One of the most important factors influencing the corrosion behavior of alloys is the galvanic corrosion which can be formed between the intermetallic phases and matrix. The potential difference between the intermetallic phase and matrix is the driving force for the electrons to move from anode to cathode and form the galvanic cells. The anodic second phase degrades in contact with the nobler matrix in a galvanic cell,whereas the matrix degrades when the second phase is nobler than the matrix. Fig. 4 shows the effect of volta-potential difference and intermetallic phase fraction on the corrosion propagation at the surface where an increase in the Voltapotential difference between intermetallic phase and the matrix accelerates the matrix degradation and so the corrosion rate increases. An increase in the fraction of the second phase also provide more active galvanic cells and so the affected area by corrosion rate will linearly increase. The corrosion rate related to the micro-galvanic cells (intermetallic) can be defined by considering the volta-potential difference, showing the kinetic of reaction and area fraction of the phase showing the available sites.

Atrens et al. [17,18,85–88] have done several studies on binary alloys and investigated the effect of alloying elements on the corrosion rate and corrosion behavior of Mg alloys.However, a potential distribution study besides their alloys will probably open a new window towards the corrosion rate prediction of Mg alloys. The potential difference between the intermetallic phases and matrix can be obtained through direct measurement of potential of each phase, using OCP [89], SKPFM [90,91], and/or first principle calculation through measuring the surface potential and work function[4].

Table 3. shows the Volta-potential difference of various intermetallics relative to the matrix, obtained from the literature. Since Mg is one of the most active elements in the series of standard electrode potential and its work function(WF) is less than the majority of alloying elements, most of the intermetallic phases act as cathode for the Mg-rich matrix. But if the matrix potential increases or alloying elements with smaller work function than Mg (WF = 3.66) such as Ca (WF = 2.8), Ce (WF = 3.1), Nd (WF = 3.2), or Y(WF = 3.1) is used, the anodic intermetallic phases can be formed. As it can be seen in the following image (Fig. 5),Mg-Ce, Mg-Nd-Y, and Mg2Ca phases showed the anodic behavior relative to the matrix. But the rest of the intermetallics showed cathodic behavior.

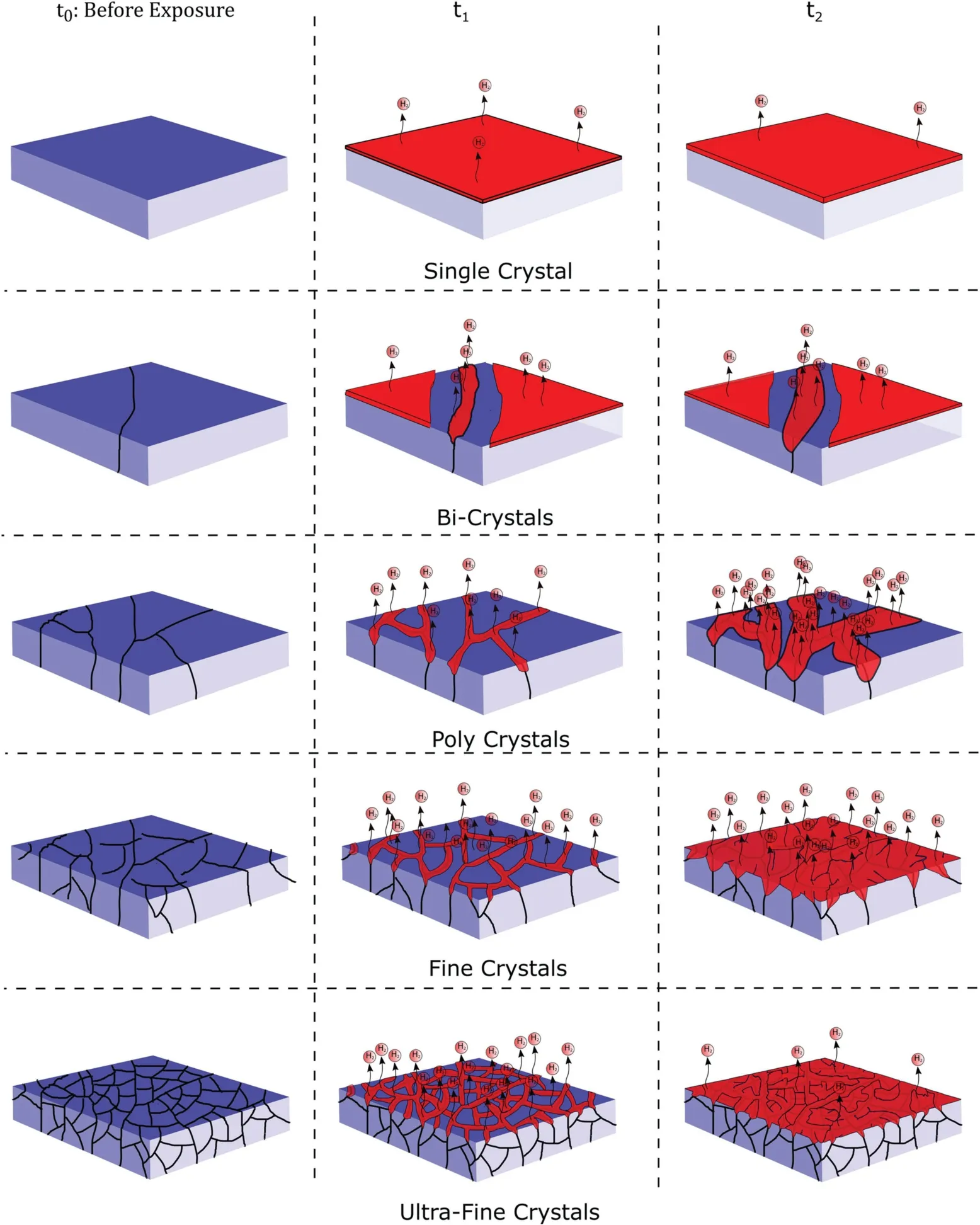
Fig. 3. Schematic representation of the effect of grain size refinement on corrosion propagation.

To understand the mechanism of corrosion propagation on the surface of materials with the anodic or cathodic second phase, the corroded surface of two materials after 0.5h immersion in 3.5 NaCl solution saturated with Mg(OH)2were compared.Fig.5(a-c)shows the Volta-potential distribution of the XM11 alloy with anodic Mg2Ca phase, Mg2Ca phase distribution,and SEM image of this alloy immersed for 0.5h,after removing the corrosion products to visualize the remaining material. As confirmed from the SKPFM results, the Mg2Ca is an anodic phase, thus dissolved during the corrosion process. A kind of filiform corrosion has also been propagated on the matrix which shows not only the second phase needs to be considered, but also matrix properties affect the corrosion behavior. This phase protected the matrix undergoing severe corrosion, but after its dissolution, the corrosion propagated on the surface as filiform corrosion and dissolved the matrix. Fig. 5(d) shows the schematic corrosion mechanism of the alloy containing the anodic phase. Here, the corrosion initiates through the dissolution of Mg2Ca and the matrix will be protected until Mg2Ca is dissolved. After the dissolution of the Mg2Ca, the matrix would not be protected and corrosion propagates on the surface, preferentially by dissolving the grain boundaries and then grains, until the surface is fully covered by the corrosion products.This kind of corrosion may form as filiform corrosion, later the passivation by corrosion products reduces the overall corrosion rate. This phenomenon could be the reason for the high corrosion rate during the initial stages of immersion. Fig. 5(e) is the volta-potential distribution of the ZAXM4211 alloy showing that intermetallic phases are cathodic with respect to the matrix. The SKPFM result confirms that both the second phases that are present on the surface are cathodic. The phase distribution on the surface of this material is shown in Fig. 5(f). Here, there are two phases including Al8Mn5which is stable in high temperatures and has a sharp morphology and (Mg,Al)2Ca+MgZn phase which forms during solidification between the dendrites and has an elongated shape. Fig. 5(g) shows the SEM image of the immersed ZAXM4211 alloy (after removing corrosion product) and clearly indicating the matrix corrosion adjacent to the second phase. Fig. 5(h) shows the schematic corrosion mechanism of the alloy containing the cathodic second phase. Corrosion initiates by the dissolution of the matrix adjacent to the second phase, the corrosion propagates along the matrix as filiform corrosion by the dissolution of the weaker sites,i.e.grain boundaries,while second phases remain undissolved. Therefore, based on the stability and compactness of the formed surface layer, the corrosion rate decreases.

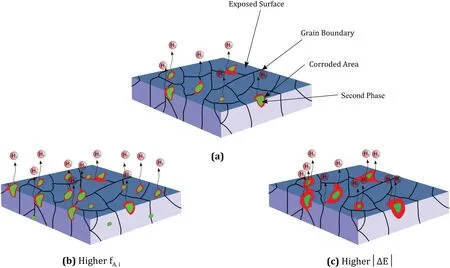
Fig. 4. Effect of Volta-potential difference and second phase fraction on corrosion rate: (a) Degradation of the matrix adjacent to the second phase for a given material, (b) more degradation due to higher Volta-potential difference and (c) more degradation compared to (a) due to higher area fraction of secondary phases.

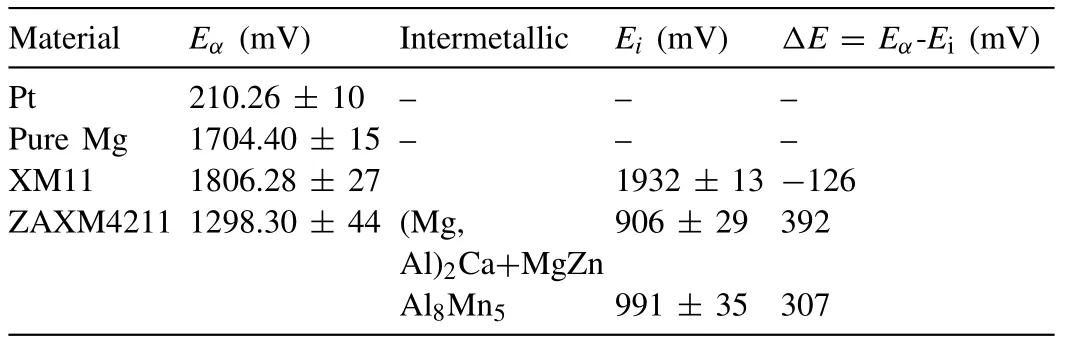
Table 2 Volta-potential values of different phases observed in Fig. 5 compared with pure Mg and Pt.

The Volta-potential values of the XM11 and ZAXM4211 alloys in addition to pure Mg and Pt have been presented in Table 2. The matrix potential has been shifted towards the more noble direction where the surface potential of pure Mg and ZAXM4211 alloy is 1704.4mV and 1298.3, respectively.The surface potential of pure Pt also was measured and it was found that the potential of Pt which is one of the noblest materials is 210mV.

Hurley et al. [3] reviewed the Volta-potential difference of various secondary phases. Here, using their reviewed and reported data, Table 3 has been presented adding other phases and making average from the available data of particular phases.

Hence,the second phase effect was divided into two mechanisms including anodic (ca×∑(fA,a×|△Ea|)) and cathodic(cc×∑(fA,c×|△Ec|)) second phases and the corrosion rate related to the second phases were defined as:

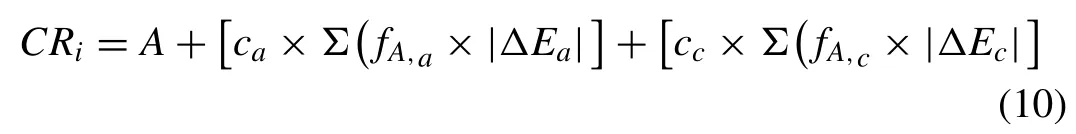
Where A, ca, cc,fA,a, fA,c, |△Ea| and |△Ec| are the corrosion rate of the material without any second phase, contribution of anodic second phases,contribution of cathodic second phases,area fraction of anodic phase, area fraction of cathodic phase,absolute value of the Volta-potential difference of matrix relative to the anodic second phase and volta-potential difference of matrix relative to the cathodic second phase, respectively.

Since an increase in △E regardless of cathodic or anodic phase increases the corrosion rate, we can use |△E|and simplify this term as [c×∑(fA,i×|△E|)] where c and fA,iare the contributions and area fraction of the second phases,respectively.

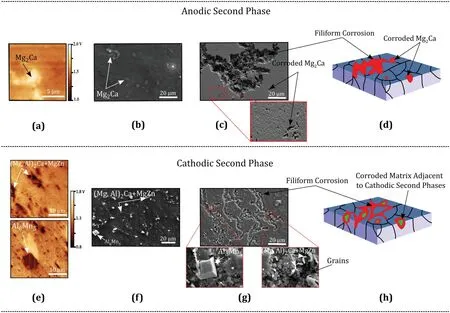
Fig. 5. Mechanisms of corrosion propagation on materials with anodic or cathodic second phases: (a) Volta-potential distribution of a Ca-containing Mg alloy(XM11 alloy) with anodic intermetallic of Mg2Ca, (b) distribution of the secondary phase on XM11 alloy before immersion, (c) SEM image after 0.5h immersion in 3.5 NaCl saturated with Mg(OH)2 solution (after removing corrosion product) showing the degraded second phases, (d) corrosion propagation mechanism of the Ca-containing alloy, (e) volta-potential distribution of a Mn, Al, Ca, and Zn-containing Mg alloy (ZAXM4211 alloy) with cathodic Al8Mn5 and (Mg, Al)2Ca+MgZn phases, (f) distribution of the secondary phases on the ZAXM4211 alloy before immersion, (g) SEM image of the immersed ZAXM4211 alloy (after removing corrosion product) showing the corroded matrix adjacent to second phases and (h) corrosion propagation mechanism of the alloy containing the cathodic phases [19,92].

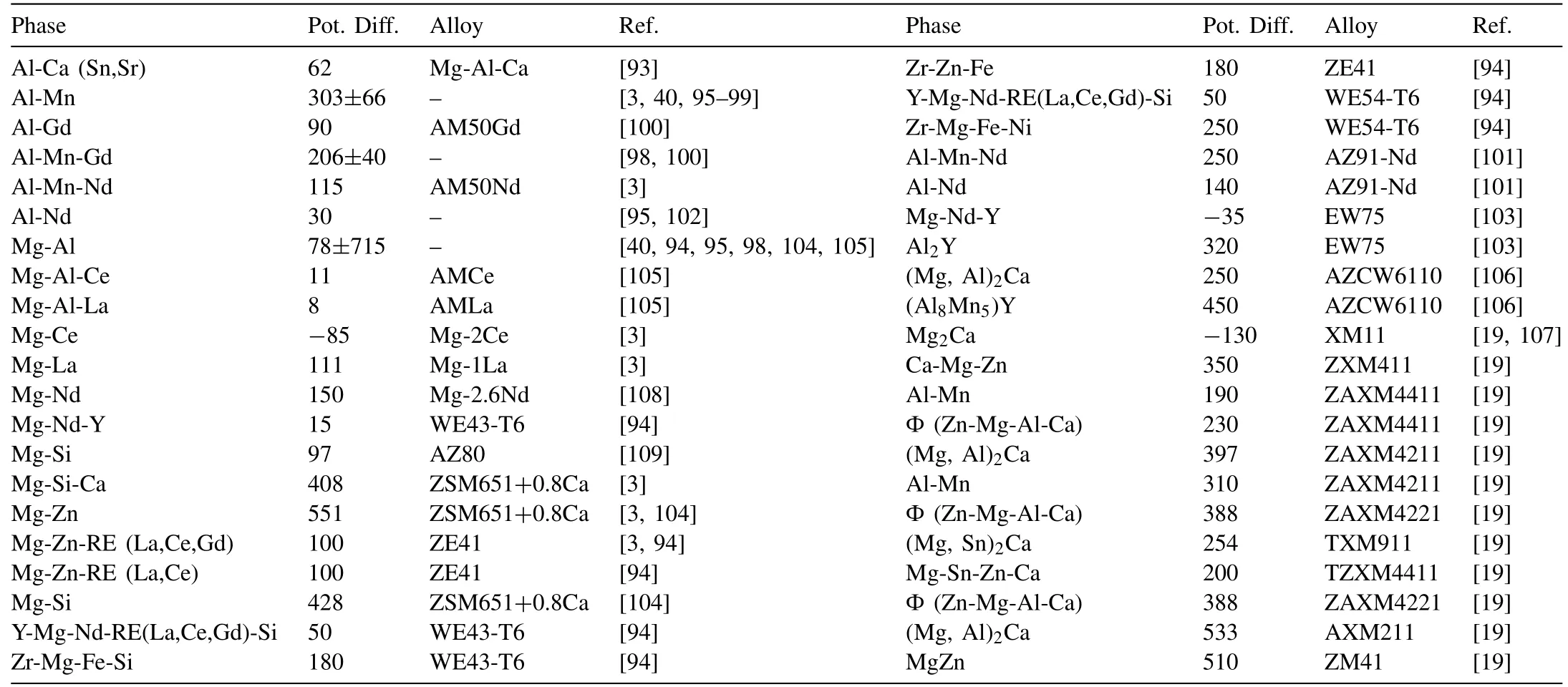
Table 3 Volta-potential difference of different intermetallics with matrix for magnesium alloys.

Fig. 6. The SEM image of the 0.5h immersed ZAXM4211 alloy: (a) extruded, (b) MDF180 and (c) MDF300.

Fig. 6 presents the surface analysis of the ZAXM4211 alloy produced in various conditions. The Volta-potential distribution presented in Fig. 5 and Table 2 showed the intermetallic phases in this alloy are cathodic. This fact was proved by SEM images where, after immersion and removing corrosion products, the second phases are intact. From Fig. 6,it is clear that the grain boundaries have been corroded and so the effect of grain boundaries as well as the second phase needs to be considered.

1.1.4. Corrosion rate formulation

Total corrosion rate equation based upon the microstructural parameters can be written as:

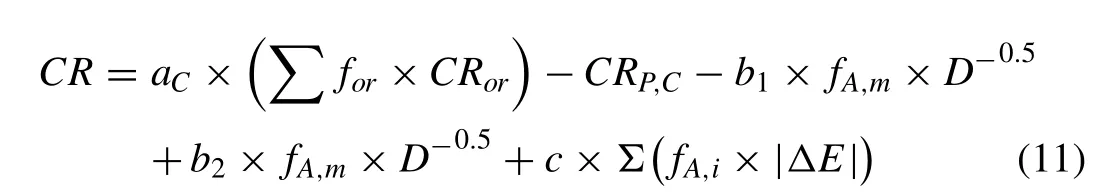
Where the first term (aC×(∑for×CRor)) is the corrosion rate of grains related to the crystallographic texture (orientation),change in surface energy by the addition of alloying elements to pure metal or changing the dislocation density of grains.CRP,Cis the passivation effect which can be changed by the alloy composition change. In present study, the texture effect has been assumed to be constant, due to the randomized texture. However, when the basal planes fraction changes, the area fraction of each orientation should be considered to analyze the corrosion results. Therefore, the above-mentioned Eq. (11) can be re-written as follows;

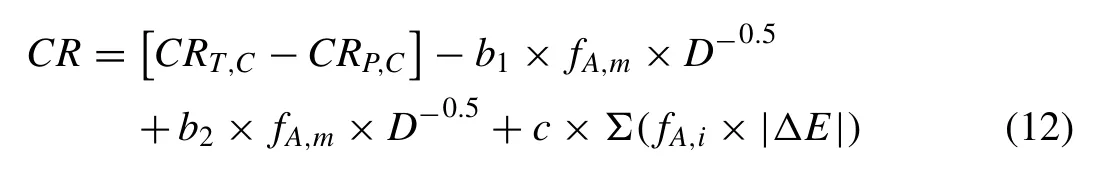
Considering CRT,C– CRP,C=CR0;

We may further consider b2-b1=b to combine the intrinsic and extrinsic effects of grain size and rewrite the Eq. (13) as Eq. (14) which is proposed as a final equation:

CR0is related to the matrix surface energy (changing by the concentration of the solute atoms and density of dislocations)and the distribution of different orientations. The contribution of grain size in the corrosion rate is denoted as “b”, which is related to the corrosive solution.It should be kept in mind that this value is positive for very large grains and negative for fine grains (the critical point is related to the solution). The contribution of the second phase, ‘c’, could be changed by the type of secondary phases(anodic,cathodic),and corrosive solution.

The corrosion rate is intensely affected by the solution type[110–114]. In fact, the solution type will change all CR0,b and c parameters. By changing the concentration of NaCl in the aqueous solution, Liu et al. [110] found that the corrosion rate is directly related to Cl−ion concentration. They mentioned that the higher concentration of NaCl results in the breakdown of the surface film, so CR0needs to be decreased hereby increasing the NaCl concentration. However,once the surface film is broken down, the second phase and grain boundaries will be activated because of solution exposure. Hence, their contribution (b and c parameters) should also be changed.

It can finally be mentioned that, considering the effect of alloy composition, grain size, and the galvanic cell can predict the corrosion rate with a good agreement as shown in Fig. 7. The related values and conditions of the corrosion rate measurement methods have been given in Table 4.

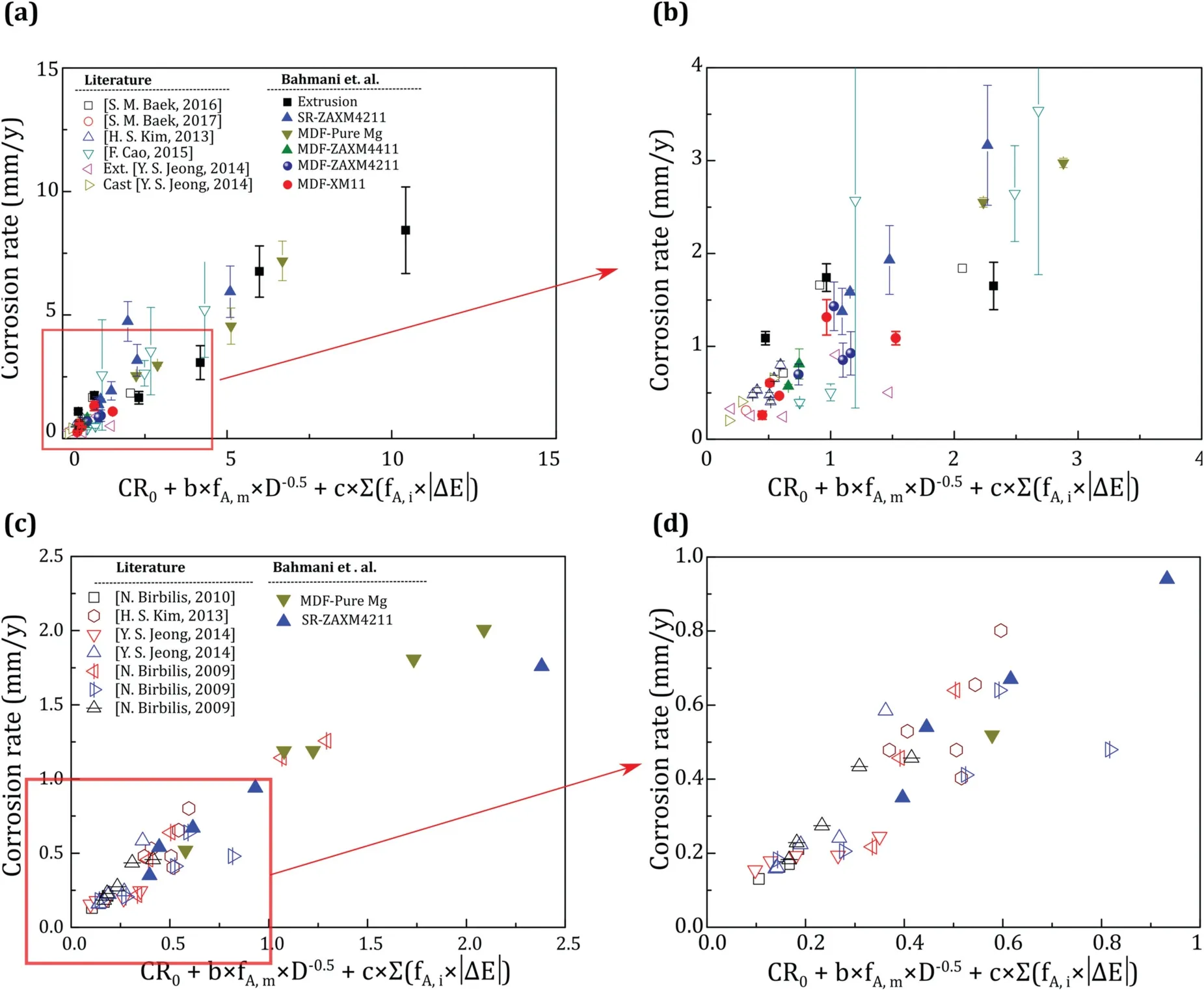
Fig. 7. (a) The experimental corrosion rate versus corrosion rate obtained by the proposed model. (a) and (b) the corrosion rate measured by hydrogen evolution or weight loss methods and (c) and (d) the corrosion rate measured by the electrochemical study.

In case of data for which the fraction of phases has not been directly mentioned in the paper, the phase fraction was measured by image analysis from the available data [17,86]or JMatPro commercial software [115]. If the volta-potential has not been measured, the available volta-potential difference values were used in Table 3. To avoid a messy graph,the graphs were separated to those data related to the hydrogen evolution or weigh loss in Fig. 7(a) and (b) and (c) and(d) are related to the electrochemical study. Since the electrochemical corrosion rate in Mg alloys is less than that of obtained by hydrogen evolution and weight loss [85, 116],lower CR0, b and c values need to be used for the proposed model. For example, as can be seen in Table 4, CR0, b and c values used for the corrosion rate calculation of rolled and annealed AZ61, reported by Kim et al. [44] are 0.5, −0.25 and 0.01 respectively for the weight loss rate, while the same parameters have the values of 0.2, −0.15 and 0.01 respectively when CR was calculated from the electrochemical polarization test.Moreover,various solutions have different intensities in corroding the exposed alloy. For instance, increasing the Cl−ions by adding more NaCl, increases the corrosion rate because of accelerating the anodic reaction and increasing the Mg dissolution. So in this case of solutions with a higher tendency for degradation, higher values are required for the balancing parameters.

Another point which is considered is the second phases that are anodic relative to the matrix have different b value comparing to the cathodic phases.For example,b value in the study of Birbilis et al. [115] for the Mg-Ce alloys containing Mg-Ce phase which is anodic against Mg matrix[3]is 3 times higher than that of the Mg-La and Mg-Nd alloys.Same results were achieved by the authors where b value in the case of an alloy containing Mg2Ca phase which is anode was higher than that of other cathodic phases (please see Tables 3 and 4). This is due to a different mechanism of corrosion for the alloy containing cathodic and anodic phases, as it has been seen in Fig. 5. However, the agreement of results between calculation and actual corrosion rates of all Mg alloys in the graph of Fig. 7 shows that both types of alloys can be used in this equation just by different balancing values.

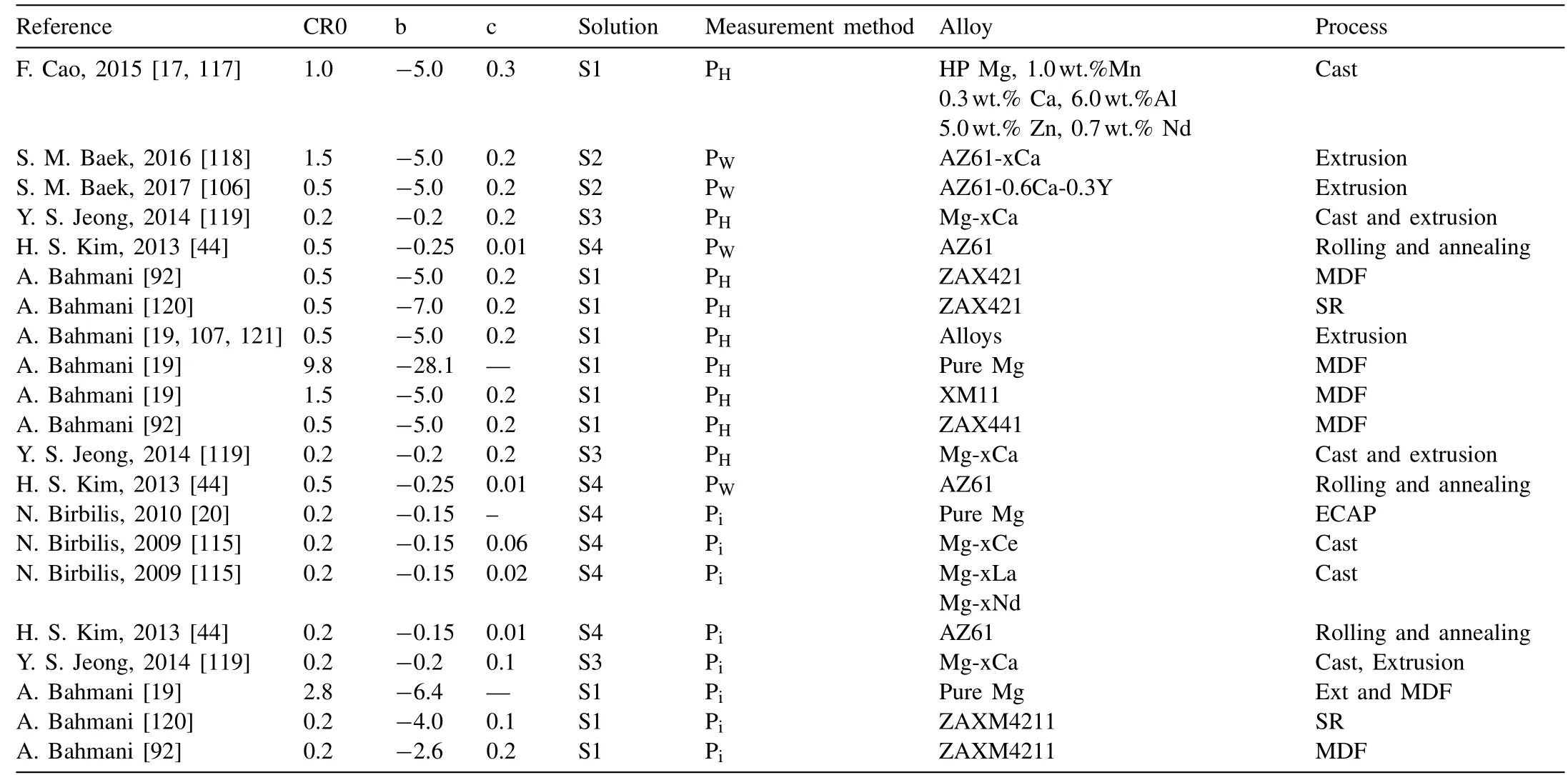
Table 4 The conditions of the various studies in the Fig. 7. Solutions are: S1: 3.5wt.% NaCl with Saturated Mg(OH)2, S2: 3.5wt.% NaCl, S3: Hank, S4: 0.1M NaCl.Corrosion rate measuring methods are: PH: Hydrogen evolution, PW: Weight loss and Pi: electrochemical polarization.

2. Conclusions

An attempt was made to model the corrosion rate of Mg alloys based on the microstructural parameters. This model can be applicable for all the alloys; however, the main focus of this paper was on various Mg alloys. Based upon the explained results, the following conclusions were drawn:

Corrosion rate can be calculated by considering the role of composition, grain size and second phases and other affecting parameters can also be applied in these terms.

- The alloy composition influences the corrosion rate through several ways such as changing the surface potential of different orientations, changing the passivating layer properties and producing second phases. The second phase was formulated as an independent term here, while the passivation and surface potential can be considered as a term named as CR0.The other parameter which can influence this term is the texture, where the basal texture has been proven to be more corrosion-resistant than the others.

- By considering the effect of grain boundaries, grain size may affect two different ways including acceleration of the corrosion in non-passivating solutions or in very large grain materials (such as single crystal) or providing more coherent and uniform passive film and protecting the substrate from further corrosion in fine and ultrafine grains and also in passivating solutions.

- The effect of second phases was included by considering their potential difference with matrix and area fraction.

- Regarding the above-mentioned parameters, an experimental equation was proposed and explained by all the pa-

rameters where it has a good match with our results and available literature.

- Moreover, a material which has a very low corrosion rate was found in our work where its corrosion rate is much less than high purity Mg.

Acknowledgment

This work was supported by the National Research Foundation grant (2015R1A2A1A01006795) funded by the Ministry of Science and ICT of Korea through the Research Institute of Advanced Materials.