A review on thermal conductivity of magnesium and its alloys

Shubo Li, Xinyu Yang, Jiangtao Hou, Wenbo Du

College of Materials Science and Engineering, Beijing University of Technology, Beijing 100124, P.R. China

Abstract This review summarizes recent researching works the thermal conductivity of Mg–Zn, Mg–Al, Mg–Mn and Mg–RE alloys. Solute atoms, heat treatment, deformation and temperature, which have significant influence on the thermal conductivity of magnesium alloys, are highlighted. For an individual solute atom, its effects on thermal conductivity are highly dependent on its chemical valence, radius and extra-nuclear electrons. The thermal conductivity of Mg alloys is decreased by solution treatment, but improved by aging and/or annealing treatments. As for the deformed Mg alloys, the thermal conductivity along transverse or normal direction is superior to that of along extrusion or rolling direction. We expect this review is helpful for those who are working on developing Mg alloys with superior thermal conductivity.

Keywords: Magnesium alloys; Thermal conductivity; Microstructure; Influencing factors.

1. Introduction

With the high integration in 3C (computer, communication and consumer product),removing the excessive heat produced during the operation of electronic components and heat exchangers, which causes the components to fail as a result of overheating or deformation, becomes more urgent. The demand for materials with both excellent heat dissipation and mechanical properties is increasing rapidly. Select materials with appropriate thermal conductivity is very important for achieving the best performance of components.

Magnesium(Mg)and its alloys are the lightweight metallic structural materials with some advantages such as low density,superior specific strength and stiffness [1,2]. They have extremely broad applications in the fields of 3C electronic products, automotive, aerospace and so on [3,4]. The density of pure Mg is 1.74g/cm3, it is approximately 2/3 density of aluminum,1/4 of steel and 1/5 of copper.The thermal conductivity of pure Mg is 156 W m−1K−1, which is relatively lower than that of copper (Cu, 398 W m−1K−1) and aluminum(Al, 237 W m−1K−11) [5,6]. Nevertheless, the mechanical properties of pure Mg, which exhibit ultimate tensile strength(UTS) of 11.5MPa and yield strength (YS) of 2.5MPa, are not enough to meet the actual demands as structure materials.Generally, addition of alloying elements into α-Mg matrix is a common way to improve the mechanical properties of pure Mg, but the addition can variously decrease its thermal conductivity[7–9].For example,Li et al.[7]found that the peakaged Mg–2Gd–2Nd–2Y–1Ho–1Er–0.5Zn–0.4Zr (wt.%) alloy had a relatively good high strength (UTS > 300MPa, YS >210MPa), proper ductility (elongation≈6%), but a low thermal conductivity (52.5 W m−1K−11). Therefore, enhancing the thermal conductivity of Mg alloys is of great importance.

Mg alloys exhibit great potential as heat dissipation materials owing to their smaller heat capacity and better heat dissipation effects than those of Al alloys [10–12]. Over the past decades, there have been some efforts devoting to enhancing the thermal conductivity of Mg alloys with a clear understanding of the fundamental heat transfer at the micro,nano and even molecular scales. In the present review, current researches on the thermal conductivity of several representative Mg alloys such as Mg–Zn, Mg–Al, Mg–Mn and Mg–RE are summarized. The factors such as solute atoms,heat treatment, deformation and temperature, which have significant influence on the thermal conductivity of Mg alloys, are highlighted.

2. Thermal conductivity of Mg alloys

Heat transfer is a vector in thermodynamics and occurs by conduction, convection and radiation [13,14]. Heat conduction in alloys is a mixture of molecular vibration and energy transport by free electrons. Thermal properties of materials,generally referring to thermal conductivity, thermal diffusivity and special heat capacity, are very crucial for industry applications [15,16]. The thermal conductivity of a material represents its intrinsic characteristic and is the amount of heat flow per unit area over a surface evaluated primarily in terms of Fourier’s Law. The thermal conductivity is also the reciprocal of thermal resistivity that represents the ability to resist heat transfer [17–19]. The thermal conductivity is usually denoted by κ or λ, which can be calculated using the following equation:

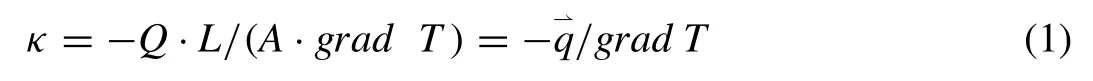
where Q is heat flow (W), L is length or thickness (m), A is the cross-sectional area of sample (m2),is the heat flux density (W m−1) and grad T is the temperature gradient (K),respectively. As known, the heat transfer is mainly achieved by free electrons moving in crystal (denoted as electron thermal conductivity κe) and phonons vibrating at lattice positions (denoted as phonon thermal conductivity κp) [20,21].The total thermal conductivity (κ) is the sum of the two contributions, that is,

The electron thermal conductivity κeis dominated for pure metals, whereas the phonon thermal conductivity κpis relatively significant in alloys. Usually, the total thermal conductivity is determined by the product of the thermal diffusivity α (m2s−1), density ρ (g cm−3) and special heat capacity Cp(J g−1K−1) [22,23]

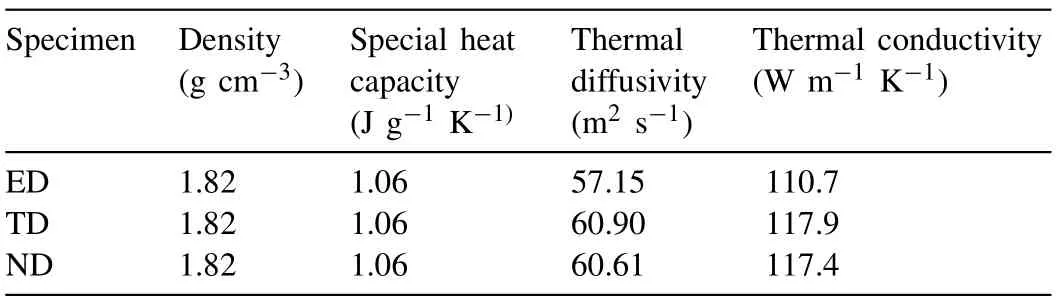
Up to now, the steady-state and transient-state methods are commonly used to measure the thermal diffusivity of alloys.The steady-state method has the advantages of clear principle and measuring the thermal diffusivity accurately and directly.However, it doesn’t work well in the continuous measurement or measures with strict requirements [24]. The transient-state method is mainly used for the measurement of the thermal conductivity and the stable specific heat capacity. Different method may result in different thermal conductivity, hence the approach for measuring the thermal conductivity should be unified in one study.

The flash method, as the most common method of thermal diffusivity test among steady-state methods, has attracted particular attention due to its convenience and simplicity. The disk-shaped sample is required 12.7mm in diameter and 3mm in thickness. Prior to measurement, the surface of sample is usually coated by graphite to ensure efficient absorption of energy from laser pulse. The temperature of sample surface increases instantaneously when the laser pulse launched by a laser source in a flash uniformly irradiates on the sample surface. Then, the energy diffuses from the hotter end to the colder end in one-dimensional heat conduction. After maintained for 10 min under the isothermal conditions, the thermal diffusivity can be obtained. Meanwhile, the corresponding temperature of the central part of the rear surface is continuously recorded and analyzed by an infrared detector,and the relation curve of temperature as a function of time is obtained [25].

where d (m) is the thickness of sample, and the half of diffusion time, t1/2(s), which is defined as the interval required for the rear surface temperature to reach half of the maximum temperature increased.

Specific heat capacity, defined as the amount of the heat absorbed or given off per unit mass of a material as it rises or falls 1K in temperature,represents the heat absorption or heat dissipation capacity of a material. A material with a larger specific heat capacity owns a stronger capacity of heat absorption or dissipation. Two methods are used to measure the specific heat capacity. One requires a Flash Analyzer, differential scanning calorimeter(DSC)and a standard sample with known specific heat capacity. The equation is represented as follows [26,27]:

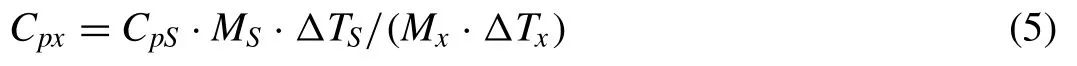
where M is the mass,and △T is the maximum temperature increase by laser irradiation. The subscripts x and S indicate the sample to be measured and the standard sample, respectively.The other is the Neumann–Kopp rule [28–30]

where Cp,iand Xiare the special heat capacity and the mass ratio of pure component, respectively. Alternatively, the measurement by DSC is more accurate and persuasive compared with the Neumann–Kopp rule.

The density ρ at elevated temperature as a function of absolute temperature T is calculated by the following equation:

where ρ0is the density at room temperature, usually obtained by the Archimedes method.

Generally, alloys with superior thermal conductivity have the ability to accelerate the heat transfer from inside to outside in the same time, which reduces the thermal stresses and inhibits the formation of harmful hot-spot defects [31]. Recently many studies focused on Mg–Zn, Mg–Al, Mg–Mn and Mg–RE alloys. In the following subsections, we summarize their thermal conductivity based on recent references.

2.1. Mg–Zn series alloys

Zn is one of the most momentous alloying elements with a maximum solid solubility of 6.2wt.% in α-Mg matrix at the eutectic temperature [32]. The thermal conductivity and thermal diffusivity of Zn are 116 W m−1K−11and 42 m2s−1, respectively, which are inferior to 156 W m−1K−11and 87.6 m2s−1of Mg [33,34]. The Mg–Zn binary alloy shows the high thermal conductivity and poor mechanical properties due to coarse grains. To balance the thermal conductivity and mechanical properties, it is indispensable to add other alloying elements to refine the microstructure. At present, Mg–Zn–RE, Mg–Zn–Zr, Mg–Zn–Mn and Mg–Zn–Cu alloys have been successfully developed. The thermal conductivity and mechanical properties of the Mg–Zn series alloys under appropriate processing conditions are listed in Table 1[35,42].It can be found that RE-free Mg–Zn series alloys exhibit higher thermal conductivity and lower mechanical properties than Mg–Zn–RE alloys on the whole.

Particularly, the thermal conductivity of Mg–Zn binary alloys is higher than 100 W m−1K−1within the maximum solid solubility of Zn. The solid solubility of Zn in α-Mg matrix decreases by adding alloying elements, especially the element of Zr,which weakens the lattice distortion and leads to the improvement in thermal conductivity.In addition,the addition of Zr can also significantly refine grains and improve mechanical properties of Mg–Zn alloys [43,44]. Especially, in the case of the peak aged Mg–2Zn–Zr alloy, the thermal conductivity of 132.1 W m−1K−11, UTS of 279MPa, YS of 196MPa and elongation (El) of 25.2% are achieved [35]. The rolling, annealing and subsequent aging processes for Mg–2Zn–Zr alloy can coordinate well the thermal conductivity and mechanical properties. The Mg–Zn–Mn ternary alloy, which has been widely studied because of the advantages of RE-free and low cost, exhibits the thermal conductivity and UTS of above 120 W m−1K−11and 280MPa, respectively [36]. As we know,the thermal conductivity of Cu (398 W m−1K−11) is superior among all commonly used structural metals. The addition of Cu can significantly increase the eutectic temperature and further improve the thermal conductivity of Mg–Zn alloy. Pan et al. [37] developed the aged Mg–6Zn–1.0Cu alloy, which exhibited the superior thermal conductivity of 128.9 W m−1K−11and micro-hardness of 94 HV. They believed that the accelerated precipitation of MgZnCu phase was attributed to the favorable interactions between Zn, Cu and vacancies.

Generally, Mg–Zn alloys containing RE exhibit superior mechanical properties and creep resistance at elevated temperatures. Due to the requirements for applications, achieving high-strength of both UTS and YS more than 500MPa for Mg–Zn–RE alloys is a vital goal. These RE elements commonly include Er, Y, Gd, etc. Zhao and Li et al. [45–47] exploited the as-cast Mg–Zn–Er alloy with different weight ratios of Zn/Er, and the results revealed that only W-phase(Mg3Zn2Er3, face centered cubic) or I-phase (Mg3Zn6Er1,icosahedral quasicrystal) existed when the ratio was less than 1 or in the range of 6–10, respectively. The different phases have various effects on the thermal conductivity of the Mg–Zn–RE alloy. Considering the influence of W-phase,Shi et al. [41] developed the as-cast Mg92Zn4Y4and Mg92Zn4Y3Gd1alloys with W-phase, and the results indicated that the existence of net-like continuous W-phase in grain boundaries could rise grain boundary strengthening effect and consume the solute elements in the matrix to promote the long-distance movement of phonons, thus, improve the thermal properties. Hu et al. [40] measured the thermal conductivity of the as-cast Mg–5Zn–Y alloy containing I-phase,it was 107.85 W m−1K−11. From these results we can find that the Mg–Zn–RE alloys show lower thermal conductivity than that of Mg–Zn binary alloys.

2.2. Mg–Al series alloys

The maximum solid solubility of Al is 12.7wt.% in α-Mg matrix according to phase diagram of Mg–Al binary alloy [48]. The as-cast and the deformed Mg–Al series alloys are widely used owing to the proper mechanical properties. However, it is concluded that the thermal conductivity of Mg alloys decreases dramatically by Al addition [49].Thermal conductivity of the as-cast Mg–1.5Al alloy is only 100 W m−1K−11owing to the solid solution of Al [7]. In Mg–Al alloys, the main strengthening phase is Mg17Al12phase, which has a lower melting point. The Mg17Al12phase is easy to soften and dissolve at a high temperature, corresponding to increasing the concentration of Al in α-Mg matrix. This would be resulting in a rapid decline in thermal conductivity of Mg–Al alloys.

Mn, Sn, Zn and RE as alloying elements are commonly used for Mg–Al series alloys. These alloying elements are prone to form high melting point phases and reduce the Mg17Al12phase simultaneously. In recent years, many researchers have performed plenty of studies on the thermal conductivity of Mg–Al series alloys [9,49,52]. Table 2 lists the most but not all of the thermal conductivity of Mg–Al series alloys. It can be found that the as-cast AZ91 alloy, as one of the commercial alloys, shows lower thermal conductivity of 51.2 W m−1K−11. The as-cast AM20 and AS21 alloys show the thermal conductivity of 97 W m−1K−11and 68 W m−1K−11, respectively. There are two reasons for the decline in the thermal conductivity of AS21 alloy, one is a fact that all Al is dissolved into α-Mg matrix, the other is the fine Mg2Si precipitate reduces the thermal conductivity more significantly.

2.3. Mg–Mn series alloys

Mg–Mn series alloys are regarded as a new type of Mg alloys, which have excellent corrosion resistance, good creep resistance and low cost. Some thermal conductivity and mechanical properties of Mg–Mn series alloys are listed in Table 3 according to Ref. [8]. The thermal conductivity of Mg–Mn alloy with 0.5wt.% Mn addition is reduced by approximately 20 W m−1K−11and the UTS is improved about 200MPa compared with pure Mg. With increase in Mn content, the thermal conductivity of the as-cast and the deformedMg–Mn alloys decreased. In order to develop Mg–Mn alloys with high strength and moderate thermal conductivity,RE is usually required. For example, the UTS and YS of the extruded Mg–Mn alloys can be enhanced by Ce addition,which is mainly related to the precipitated phases. In general,the as-extruded Mg–0.5Mn-xCe alloys exhibit higher thermal conductivity than the as-cast counterparts, which is attributed to the weakened basal texture. In addition, the thermal conductivity of the as extruded Mg–Mn alloys is higher than that of the as-extruded Mg–Al and Mg–Zn alloys when the solute content is greater than 0.5 at.% [8,9,53].

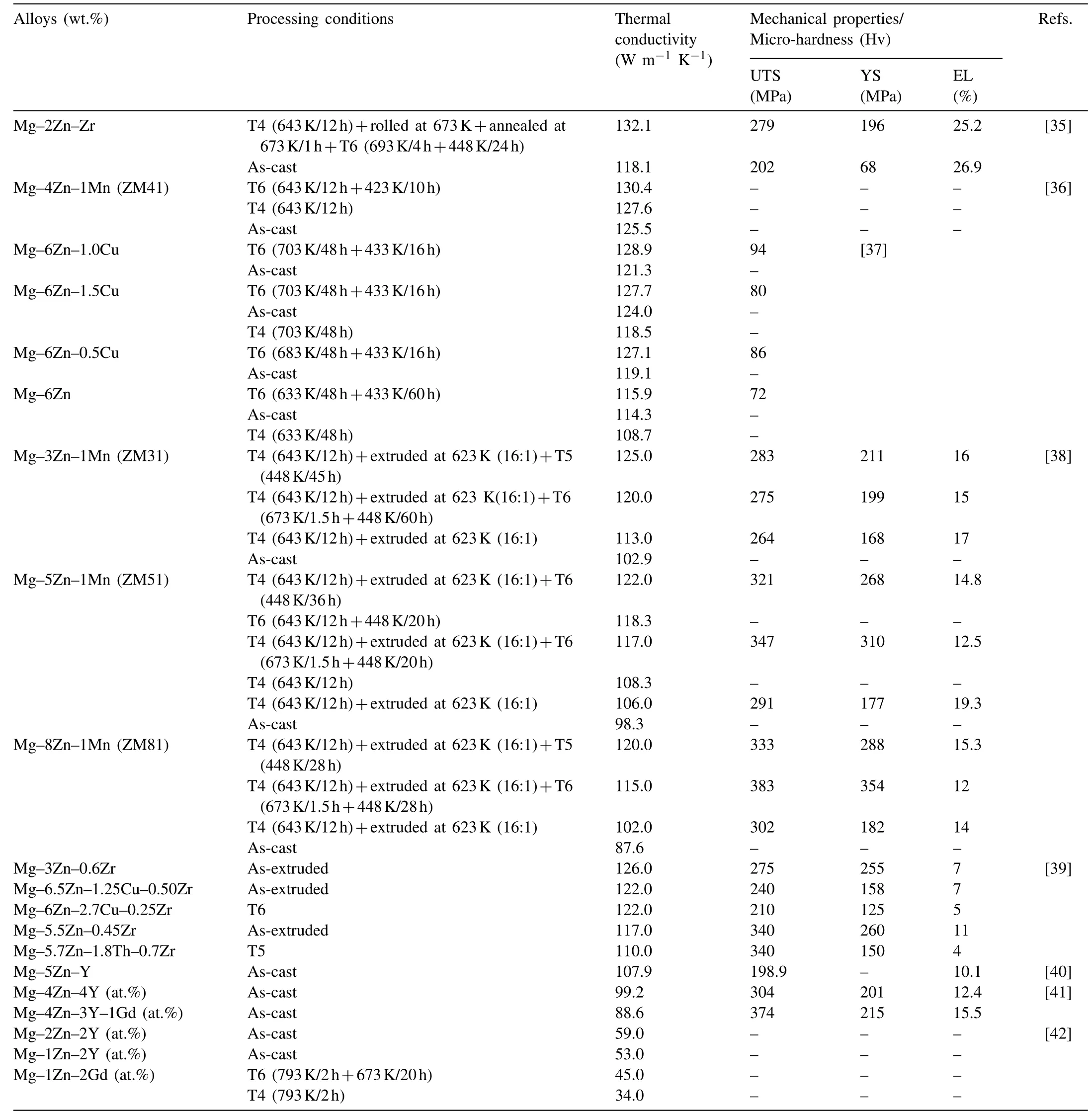
Table 1 Thermal conductivity and mechanical properties of Mg–Zn series alloys.

2.4. Mg–RE series alloys

Rare earth (RE) elements not only improve the strength but also enhance the plasticity and corrosion resistance of Mgalloys [54–57]. Generally, the added RE can significantly purify the Mg melt and induce the formation of strengthening phases via appropriate heat treatment [58–60]. Nevertheless,RE can dramatically decrease the thermal conductivity of Mg alloys. It is unsatisfactory that the thermal conductivity of Mg–RE alloys is still low. The thermal conductivity and mechanical properties of several Mg–RE series alloys are summarized in Table 4. It can be seen the thermal conductivity of the aged Mg–11Y–5 Gd–2Zn–0.5Zr alloy is only 23 W m−1K−11.

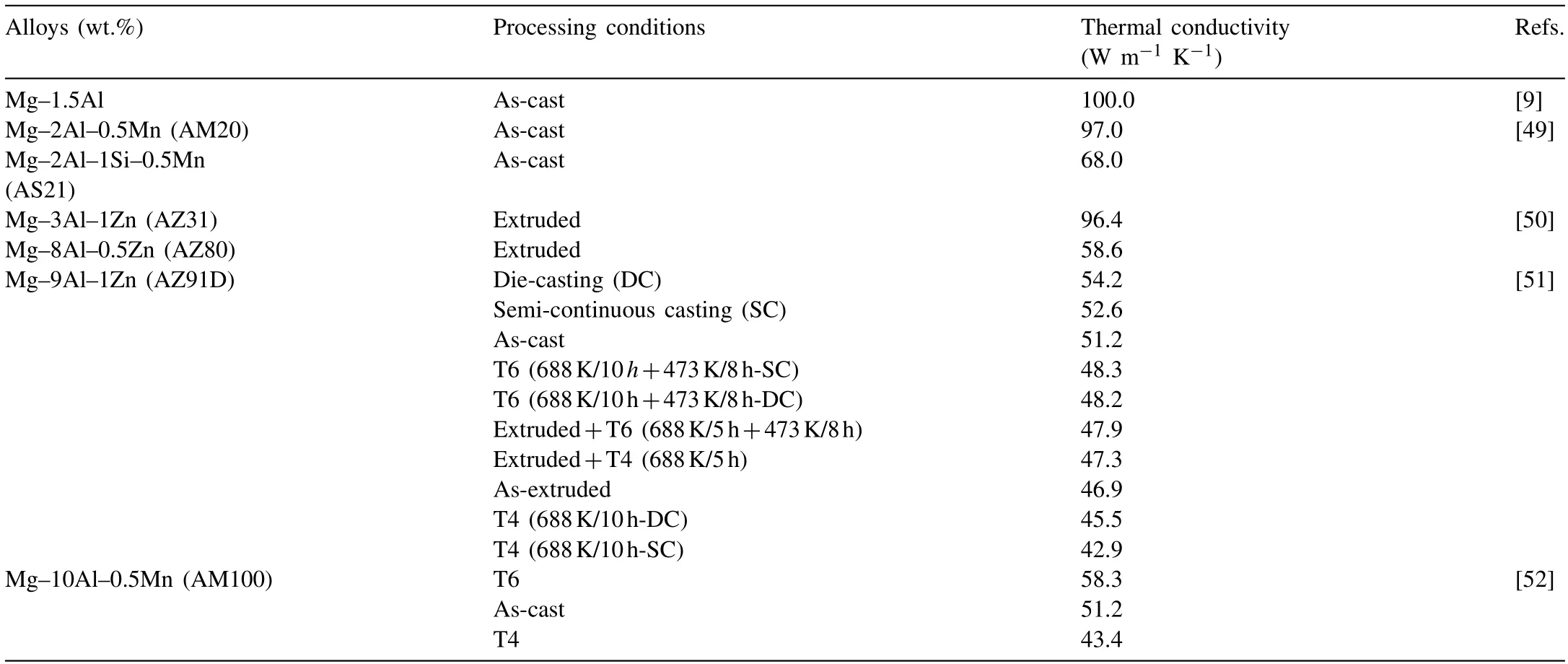
Table 2 Thermal conductivity of Mg–Al series alloys.

Table 3 Thermal conductivity and mechanical properties of Mg–Mn series alloys [8].

The Zn addition into binary or ternary Mg–RE alloys to form LPSO (Mg12YZn, long-period stacking ordered) structure can achieve superior mechanical properties at room temperature[61–66].The study on the thermal conductivity of the Mg–RE alloys with LPSO structure becomes a new hot topic,and the relevant opinions are contradictory. Shi et al. [41] analyzed that the LPSO structures could hinder the diffusion of phonons in grain interior or at grain boundary. The reduced thermal conductivity is mainly attributed to the higher number of the LPSO structures, stacking faults and grain boundaries scattering. However, Yamasaki et al. [42] proposed that the LPSO structures consumed the RE in α-Mg matrix and could further improve the thermal conductivity. Unfortunately, compared with other series alloys, the research data on the thermal conductivity of Mg–Zn–RE alloys containing the LPSO structures has been rarely reported.

Based on the reported investigations, we summarized the thermal conductivity and ultimate tensile strength of some Mg alloys, as shown in Fig. 1. It can be found that the thermal conductivity of Mg–Zn and Mg–Mn series alloys are generally higher than that of Mg–Al and Mg–RE series alloys.The balance between the thermal conductivity and mechanical properties is still a long-term challenge in the functional application of Mg alloys. More attentions should be paid onalloy design and optimizing the manufacturing processes to develop Mg alloys with superior thermal as well as mechanical properties.

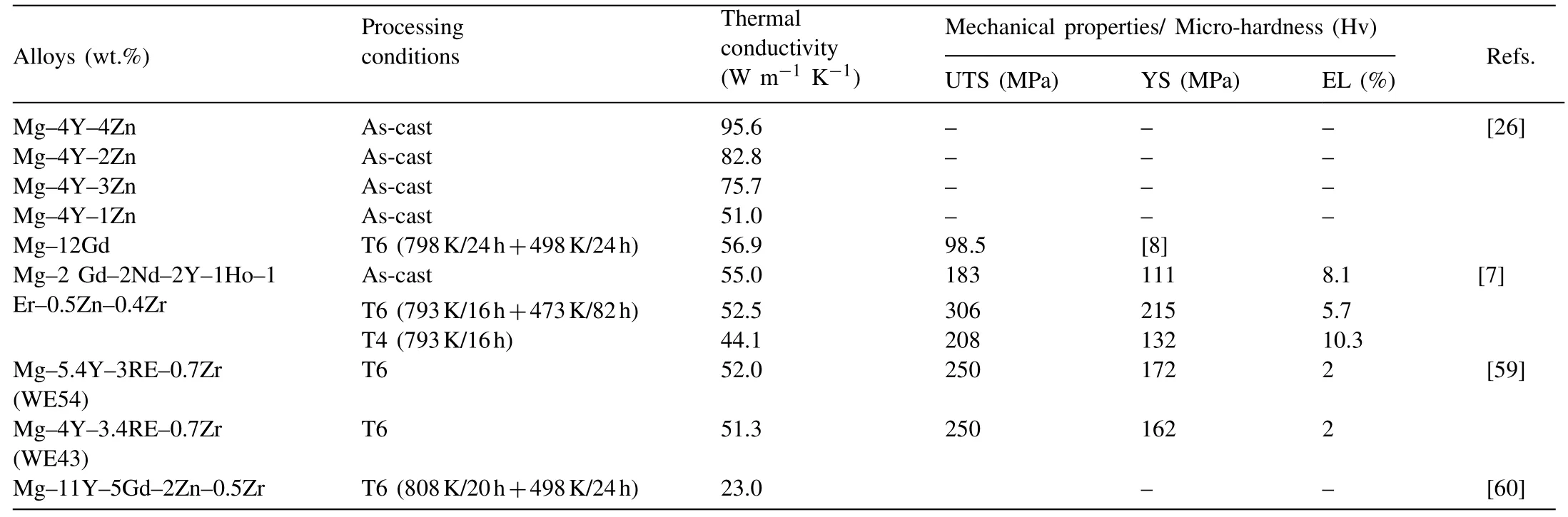
Table 4 Thermal conductivity and mechanical properties of Mg–RE series alloys.

Fig.1. Thermal conductivity and ultimate tensile strength of some Mg alloys.

3. Factors influencing the thermal conductivity of Mg alloys

3.1. Effects of solute atoms on thermal conductivity

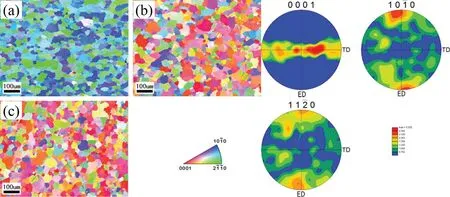
The thermal conductivity of Mg alloy is highly dependent on its composition. Unfortunately, alloying elements that behave as the heterogeneous atoms of α-Mg matrix generally decrease the thermal conductivity of Mg alloys. Fig. 2 indicates the sequence in which several solute atoms deteriorate the thermal conductivity of α-Mg matrix [53,67–69]. The added solute atoms always have bad influence on thermal conductivity because the fact that the solute atoms could induce the lattice distortion of α-Mg matrix, change the lattice parameter c/a, and shorten the mean free path of electrons and phonons by substituting Mg atoms [70–73].

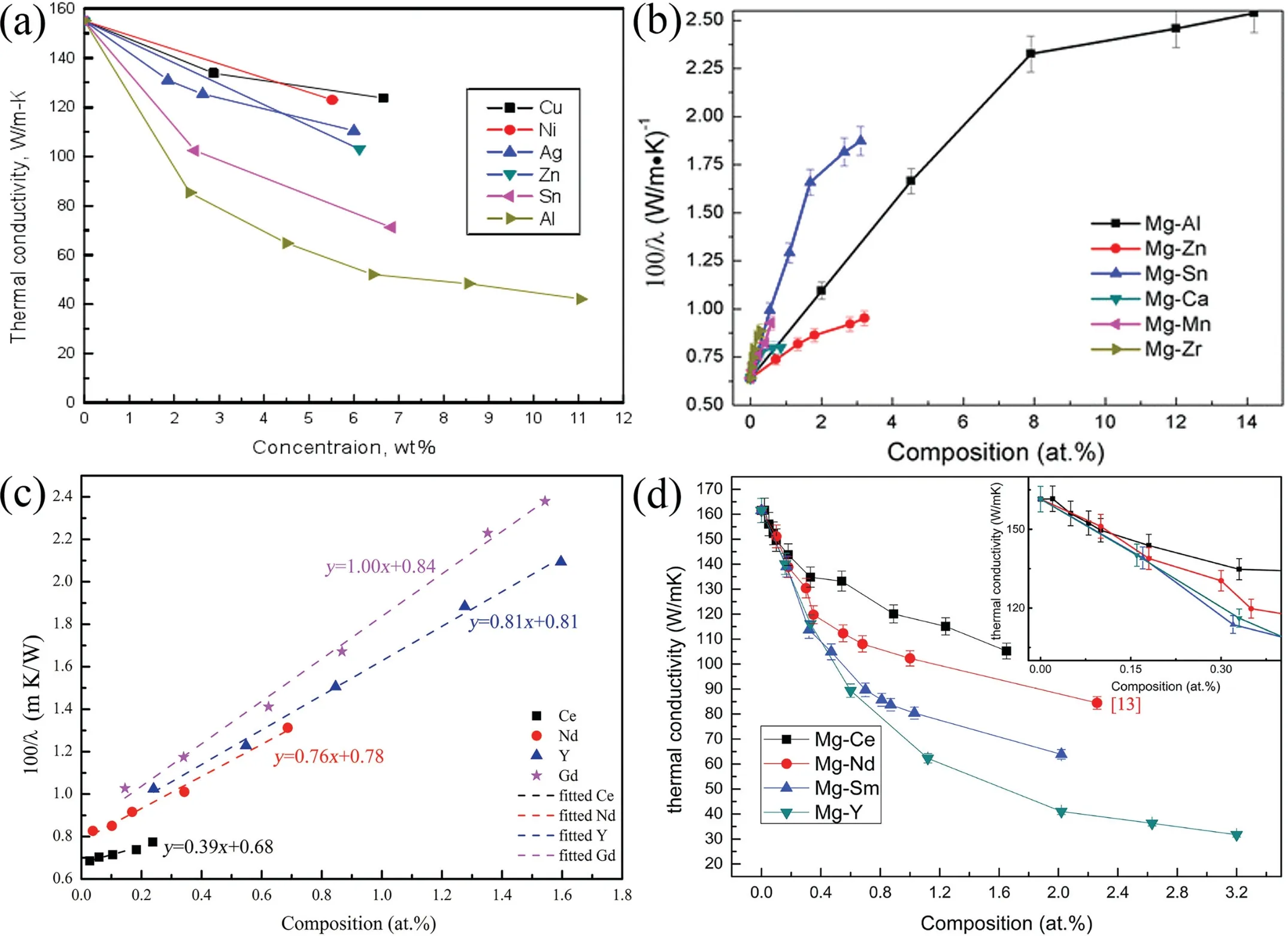
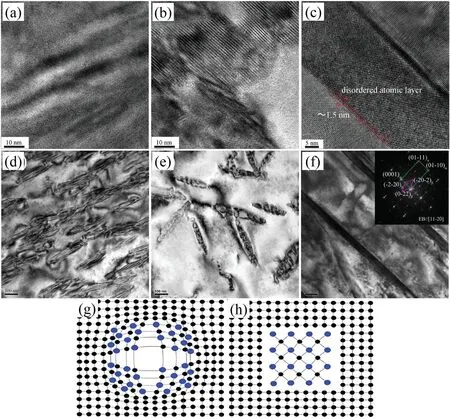
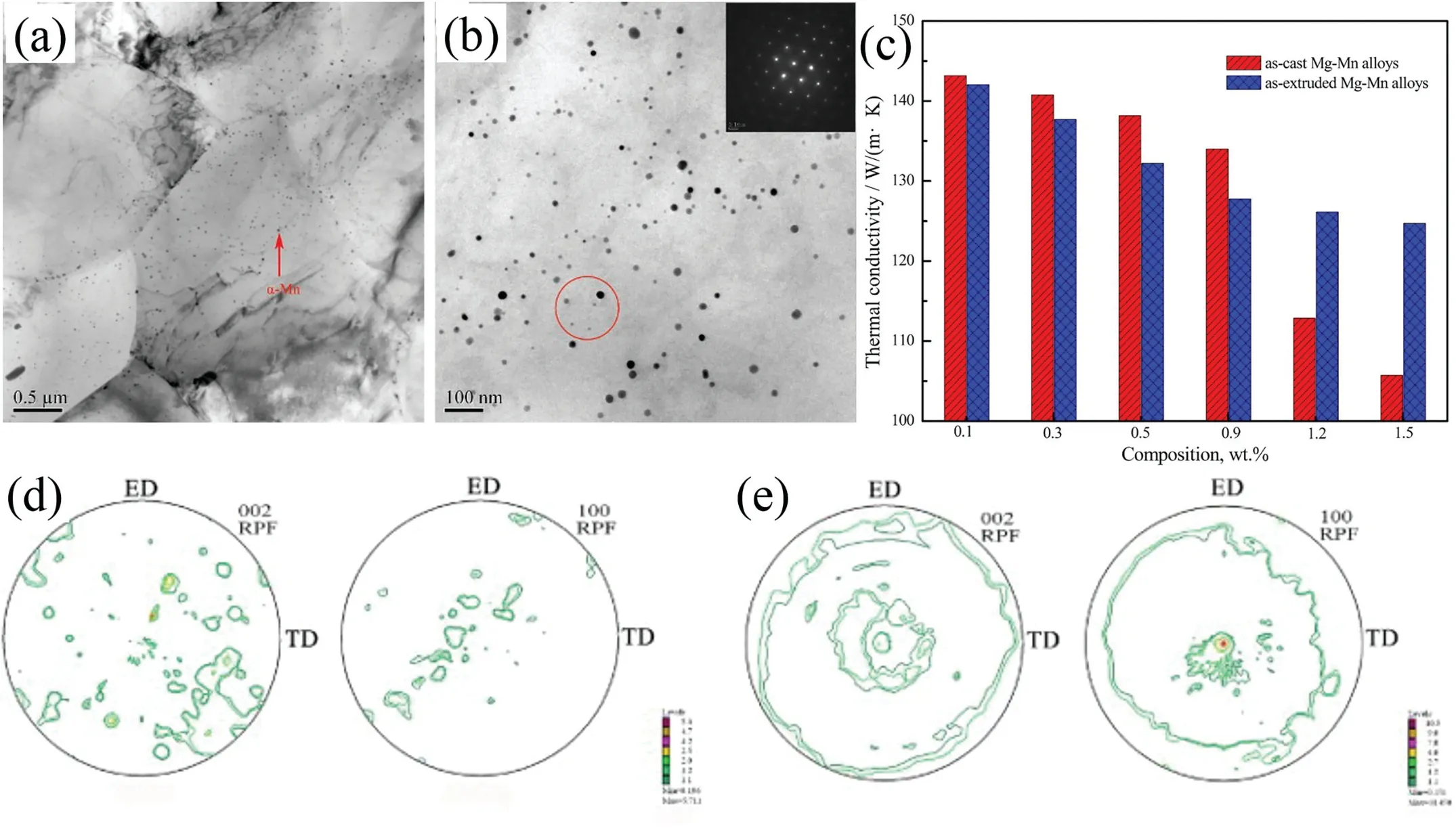
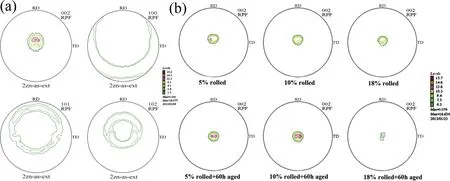
The occurrence of lattice distortion is mainly due to two reasons. On one hand, the replacement of Mg atoms by the solute atoms is suggested to causing the lattice distortion because of the difference in atomic radius between the solute atoms and Mg atoms; On the other hand, the difference in chemical valence of the solute atoms and Mg atoms can alter the shape of the Brillouin zone of Mg [68]. In addition, the solute atoms with the higher solubility can arouse more severer lattice distortion, which results in the c/a ratio deviating from that of pure Mg. The maximum solid solubility of Gd,Y, Nd and Ce in α-Mg matrix are 4.53, 3.35, 0.63 and 0.09 at.%, respectively [68]. These four RE elements have different influence on the thermal conductivity of Mg alloys in the sequence of Ce

3.2. Effects of heat treatment on thermal conductivity

Generally, the solid solution treatment tends to reduce the thermal conductivity of Mg alloys due to the increase in the solute atoms dissolved into α-Mg matrix [74–76]. According to Refs. [69,77,78], the reduction in thermal conductivity caused by the solute atoms is approximately several orders larger than that by the second phases. It is calculated that the reduction in the thermal conductivity of Mg–RE alloys is about 123.0 W m−1K−1with per 1 at.% RE addition in the form of solute atoms or 6.5–16.4 W m−1K−11in the form of intermetallic compounds in α-Mg matrix [69]. However, Bai et al. [51] studied the as-extruded AZ91D alloy and found that dislocation-recovery, grain-coarsening and defectdecrease after the solid solution treatment were beneficial to the thermal conductivity of AZ91D alloy although the Al content increased in α-Mg matrix.

Different from the solid solution treatment, the aging treatment improves the thermal conductivity of Mg alloys[79–84],as shown in Fig. 3. During the aging treatment, a large number of solute atoms precipitated from α-Mg matrix to form second phases, which will weaken the lattice distortion, resulting in the improvement in thermal conductivity. The aging treatment concurrently increases the mean grain size and reduces the original grain boundary defects, which is also beneficial to improving the thermal conductivity. Moreover,the thermal conductivity can be optimized significantly via aging time. As shown in Fig. 3(d), the thermal conductivity of the Mg–5Sn alloy increased from 87.5 W m−1K−11up to 122 W m−1K−11after aging treatment for 120h [83].

Fig. 2. Effects of solute atoms on the thermal conductivity of α-Mg matrix reported in Ref.: (a) [53], (b) [67], (c) [68], (d) [69].

It is considered that the interface between the precipitated phases and α-Mg matrix also has significant influence on the arrangement of matrix atoms around the precipitated phases[8,85]. During aging treatment, the interface between precipitates and matrix transformed from coherent at under aging (4h, Fig. 4(a, d)) or semi-coherent at peak aging (24h,Fig. 4(b, e)) to incoherent at over aging (300h, Fig. 4(c, f)).As illustrated in Fig. 4(a, d, g), the coherent interface induced serious lattice distortion owing to the large stress field introduced by the occupation of α-Mg lattice nodes by the atom of the precipitated phase.The free movement and conductions of electrons as well as phonons are limited seriously due to this kind of lattice distortion, leading to the decrease in the electrical or thermal conductivity of Mg alloys. In contrast,the incoherent interface between the precipitates and α-Mg matrix produced relatively minor lattice distortion, which is shown in Fig. 4(c, f, h). In addition, although the formation of the second phases will produce new surface defects and they are disadvantage for thermal conductivity, the thermal conductivity of Mg alloy is more sensitive to the solute atoms than the second phase. Therefore, the aging treatment is an effective method to improve the thermal conductivity of Mg alloys, and it can enhance the thermal conductivity as well as mechanical property simultaneously. This conclusion is also applicable to the other alloys such as Al and Zn alloys[86,87].

3.3. Effects of deformation on thermal conductivity

The thermal conductivity is affected by deformation usually governed by various factors such as texture, grain size and precipitate [88,90]. Owing to the preferential orientation of recrystallized grains and the hexagonal close-packed (hcp)structure of Mg alloy, its thermal conductivity exhibits significant anisotropy [91–93]. As shown in Fig. 5 and Table 5,Yuan et al. [91] reported that the thermal conductivity of asextruded ZM51 alloy along the transverse direction (TD) or normal direction (ND) was superior to that of the extrusion direction (ED). The close arrangement of atoms along a-axis(<11¯20> direction) and the strong texture on {0001} plane are contributed to the decrease in the thermal conductivity.In other words, the mean free path of electrons and phonons is relatively shorter along <11¯20> direction and on {0001}plane. These results may be referred for the as-extruded products which in need of dissipating heat in a certain direction.

Fig. 3. Thermal properties of Mg97Zn1Y2, Mg96Zn2Y2 and Mg97Zn1Gd2 alloys: (a) thermal diffusivity, (b) specific capacity, (c) thermal conductivity [42];thermal conductivity as a function of unit cell volume of α-Mg phase and aging time of Mg-5Sn alloy (d) [83].

Table 5 Thermal properties of as-extruded ZM51 alloy [91].

However, dynamic precipitation and weakening of the basal texture have positive effects on the thermal conductivity[89,90]. Zhong et al. [89] compared the thermal conductivity of the as-cast and the as-extruded binary Mg–Mn alloys with different Mn contents at room temperature (Fig. 6(c)). The as-cast Mg–Mn alloy exhibited a higher thermal conductivity than the as-extruded alloy in the case of Mn < 1.2wt.%,because the mean grain size decreased and the typical basal texture was generated after extrusion (Fig. 6(d, e)). The similar results have been found in Refs. [94,95]. However, when the content of Mn was over 1.2wt.%, the fact was just the other way because the nano-particles precipitated from α-Mg matrix during hot extrusion, as illustrated in Fig. 6(a, b). In addition, as shown in Fig. 7, Pan et al. [96] reported that the large strain rolling could increase the electrical conductivity of Mg alloys owing to the weakening of basal texture.Therefore, it is suggested that the texture weakening is a preferred method to develop the Mg alloys with superior thermal conductivity.

3.4. Effects of temperature on thermal conductivity

The thermal conductivity as well as other thermal properties of an alloys is extremely sensitive to temperature [97–100]. Because the fact that the heat conduction is mainly achieved by the movement of free electrons and phonons, the thermal conductivity of alloy can be changed drastically with increase or decrease in temperature.

Fig. 4. HRTEM and bright field images of the as-solutioned Mg-12Gd alloy at 498K for various aging times: (a, d) 4h, (b, e) 24h, (c, f) 300h [85]; atomic model of the coherent interface (g) and the incoherent interface (h) [8].

Thermal conductivity of pure Mg and its alloys varies differently with temperature during the higher temperature range(>300K) [88], as shown in Fig. 8(a). The thermal conductivity of pure Mg decreases with the increase of temperature because of increased phonons energy, leading to the enhanced electron-phonon and phonon-phonon scattering. Comparing with pure Mg, the thermal conductivity of Mg–Zn binary alloys increases with temperature. Due to the adding of Zn element, the impurity-electron scattering and impurityphonon scattering, which are elastic scattering, play major roles in thermal conductivity. Similarly, there is such a phenomenon for other binary or ternary Mg alloys. For instance,a study on the thermal properties of Mg–Li and Mg–Li-Al alloys as a function of temperature in the range 293–648K have been performed by Rudajevová et al.[101],the results showed that the thermal conductivity decreases with the increase of temperature.

However, the thermal conductivity in low temperature range (0–300K) also varies differently than that in the elevated temperature range (>300K). As presented in Fig.8(b), the thermal conductivity exhibits a peak in the pure Mg, Mg–0.5% Zn and Mg–1.5% Zn alloys within the extremely low temperature range 20–40K owing to the low defects and the competition between impurity-electron scattering and impurity-phonon scattering [102]. Scattering of electrons by phonons with high energy is intensified as temperature rises, thus leading to a sharp drop in electron thermal conductivity. Similar phenomenon is observed in other materials, such as Al alloys and steel so on [103,104]. Generally,

Fig. 5. Microstructures obtained from EBSD analyses, the {0001}, {10¯10} and {11¯20} pole figures on the ED-TD planes of the as-extruded ZM51 alloy: (a)ED specimen, (b) TD specimen, (c) ND specimen [91].

Fig. 6. TEM observations of the fine particles in the as-extruded Mg-1.2Mn alloy (a, b); comparison of the thermal conductivity of as-cast and as-extruded Mg–Mn alloys with different contents of Mn (c); the pole figures of Mg-0.1Mn alloy: (d) as-cast, (e) as-extruded [89].

Weidman-Franz Law (WFL) [105–107], as a function of temperature,defines the relationship between the electron thermal conductivity and the electrical conductivity, as shown in Eq.(8).

where σ is the electrical conductivity (S m−1) and L0is the Lorentz constant of 2.45×10−8(WΩK−2).According to the law, the thermal conductivity is proportional to the electrical conductivity at a fixed temperature. However, the failure of the WFL to calculate the low temperature thermal conductivity is testified. The thermal conductivity of pure Mg, binary and multi-component Mg alloys is fitted to an equation of κ=(A/T+BT2)−1+CT2in the temperature range 2–100K and the parameters A, B and C are determined [102]. The equation is also applicable for predicting the low-temperature thermal conductivity of other alloys such as Al and Cu alloys.Therefore, it is especially critical to ensure the products made of Mg alloys such as electronics to behave as we expected when they generate heat.

Fig. 7. The {0001}, {10¯10}, {10¯11} and {10¯12} pole figures of the as-extruded alloy (a); the {0002} pole figures of rolled Mg–2Zn alloys with different rolling reductions (b) [96].

Fig. 8. Temperature dependence of the thermal conductivity of as-cast pure Mg and Mg–Zn alloys: (a) at high temperature [88], (b) at low temperature [102].

4. Conclusions and outlook

This review summarized the works about the thermal conductivity of Mg–Zn,Mg–Al,Mg–Mn and Mg–RE alloys.The following comments are suggested:

(1) Aiming to develop Mg alloys with superior thermal conductivity, more attentions should be paid on decreasing the lattice distortion and increasing the purity of α-Mg matrix.

(2) Realizing the decrease in lattice defects and solute atoms would be promising to enhance the thermal conductivity of Mg alloys. Also, the texture weakening and aging treatment are optional.

(3) Although high strength can be achieved in Mg–RE series alloys, it is still a challenge to develop Mg-RE alloys with high thermal conductivity because of some well-known difficulties such as the difference in chemical valences, radius and extra-nuclear electrons between RE and Mg atoms.

(4) There is still a lot of work to be performed to build models, which can be used to evaluate the influencing of solute atom, precipitate, grain size and texture on the thermal conductivity of Mg alloys.

Acknowledgments

This work was supported by National Key Research and Development Program of China (2016YFB0301101) and Key Science and Technology Program of Beijing Municipal Commission of Education, China (KZ201810005005).