基于Simulink仿真的线性三自由度汽车操纵模型

2020-04-29张缓缓李庆望

智能计算机与应用 2020年2期

严帅，张缓缓，高超，李庆望

(上海工程技术大学，上海 201620)

0 引言

线性二自由度汽车模型虽然可以用于研究汽车操纵稳定性的基本特性[1]，但是只能反映汽车的纵向运动和横摆运动，当涉及到汽车侧翻时，此时必须考虑车身的侧倾效应，二自由度汽车模型不再能满足需求，因此，必须建立包括车身侧倾的三自由度汽车模型来同时表达汽车的侧向运动、横摆运动和侧倾运动，例如文献[2-4]以三自由度汽车模型作为控制模型，基于主动转向和直接横摆力矩的联合控制，提高了整车的抗侧翻能力。

二自由度汽车模型的理论基础已经很成熟，然而三自由度汽车模型因为涉及到车身的侧倾，需要用到更多的参数，不同的文献给出的数学表达式并不一致，喻凡等人[5]将汽车分为簧上、簧下前轴、簧下后轴三部分，并给出了考虑车身侧倾的三自由度汽车模型，然而公式很复杂，部分参数也难以获取。郭孔辉[6]将汽车分为簧上、簧下两部分并引入很多算子系数来表达汽车模型，虽然数学表达式简单，但是每一个算子系数却并不容易计算。在实际建模过程中，获取汽车参数的难度在一定程度上也代表了模型的复杂程度，因此本文在相关文献的基础上，简化了三自由度汽车模型的数学表达式，使其更容易理解和应用，并与二自由度汽车模型在不同工况下进行了仿真对比。

1 低自由度汽车操纵模型的建立

低自由度汽车操纵模型包括线性二自由度汽车模型和线性三自由度汽车模型，虽然模型简单，但是基本可以概括汽车的操纵特性，并由此引出汽车转向特性的概念，定义汽车的不足转向和过度转向[5]，而且建立低自由度汽车操纵模型也为建立更复杂的汽车模型提供了理论基础。

1.1 线性三自由度汽车模型

线性三自由度汽车模型如图1所示，其基本理论最初出现于1956年的美国康乃尔实验室，因为考虑到车身的侧倾影响，相对于二自由度汽车提高了模型精度。在建立三自由度汽车模型时，应将其分为簧上和簧下两部分并作以下假设：

(1)汽车纵向车速保持不变，前轮转角不大。

(2)汽车的垂直振动影响忽略不计。

(3)汽车的侧向加速度限定在0.4 g以下，轮胎侧偏特性处于线性范围。

(4)汽车不受空气动力作用，驱动力不大。

取固结于汽车上的动坐标系oxyz为车辆坐标系，根据右手定则[1]，汽车静止时，坐标系原点o与汽车质心重合；x轴指向前方为正；y轴指向驾驶员的左侧为正；z轴通过汽车质心，指向上方为正。

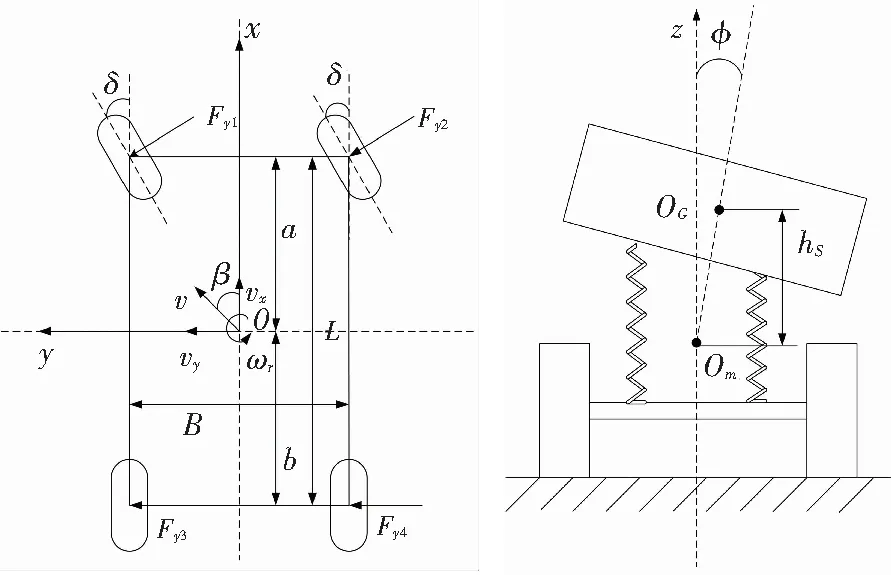
图1 线性三自由度汽车模型

在这样的坐标系下，汽车质心处的侧向加速度和簧上质量质心处的侧向加速度分别为：

(1)

(2)

其中，vx为汽车纵向车速；vy为汽车侧向车速；ωr为汽车的横摆角速度；hs为汽车簧上质量质心到侧倾轴线的距离；φ为侧倾角。

考虑到前轮转角δ不大，即cosδ≈1，根据达朗贝尔原理，则可以列出线性三自由度汽车模型的运动微分方程。

汽车沿y轴的侧向运动为：

(3)

汽车绕z轴的横摆运动为：

(4)

汽车绕x轴的侧倾运动为：

(5)

其中，m为汽车质量；ms为汽车簧上质量；Fyf为汽车前轮受到的侧向力；Fyr为汽车后轮受到的侧向力；a为汽车质心到前轴的距离；b为汽车质心到后轴的距离；g为重力加速度；Iz为汽车绕z轴的转动惯量；Ixz为汽车绕x轴和z轴的质量积；Isx为汽车簧上质量绕x轴的转动惯量；K为汽车的等效侧倾刚度；C为汽车的等效侧倾阻尼。

考虑到Ix为汽车绕x轴的转动惯量并且Ixz的数值为0，可以得到：

(6)

侧向力Fyf、Fyr可以表达为：

(7)

其中，kf、kr分别为汽车前、后轮的侧偏刚度；αf、αr分别为汽车前、后轮的侧偏角。

考虑到汽车侧倾时悬架的变形作用导致的侧倾转向、侧倾外倾、变形转向和变形外倾以及汽车本身的几何关系，汽车前、后轴的侧偏刚度αf、αr为:

(8)

其中，Ef、Er为汽车前、后轴等效侧倾转向系数；δ为汽车前轮转角。则由式(3)～(8)可以整理得三自由度汽车模型方程为：

(9)

其中，β为汽车的质心侧偏角，大小为:

(10)

在Simulink中搭建的三自由度汽车模型如图2所示。

1.2 线性二自由度汽车模型

线性二自由度汽车模型[1]如图3所示，只考虑汽车的侧向运动和横摆运动，其数学表达式为：

(11)

取X=(βωr)T为状态变量，将式(11)改写为状态方程形式:

图2 三自由度汽车模型的Simulink模块

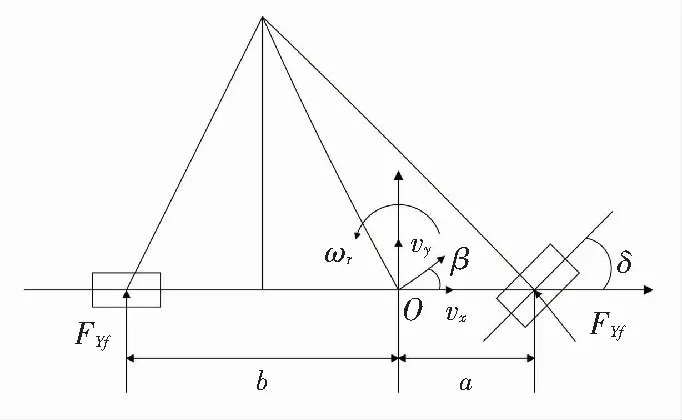
图3 线性二自由度汽车模型

(12)

(13)

(14)

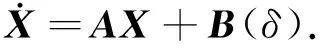
(15)

在Simulink中以状态方程形式搭建的二自由度汽车模型如图4所示，仿真参数可以编写成M文件输入到Matlab工作空间中。

图4 二自由度汽车模型的Simulink模块

2 仿真验证

汽车的转向特性与汽车的操纵稳定性密切相关，本文分别在车速为48 km/h、72 km/h和96 km/h，前轮转角δ=1°时对比线性二自由度汽车模型和线性三自由度汽车模型的角阶跃输入响应。仿真模型的主要参数取自“红旗”CA770汽车[6]，见表1。

表1 汽车模型的主要参数

注：低自由度汽车模型是单轨模型，其侧偏刚度为汽车实际侧偏刚度的2倍。

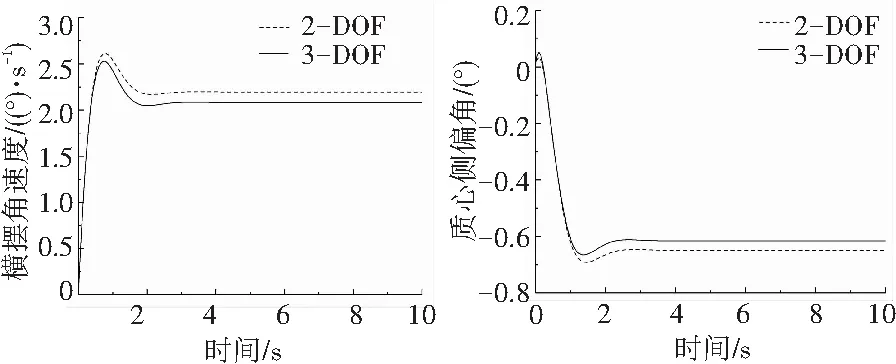
(1)车速为96 km/h的仿真结果，见图5。

(a) 横摆角速度曲线 (b) 质心侧偏角曲线

(2)车速为72 km/h时的仿真结果，见图6。

(3)车速为48 km/h的仿真结果，见图7。

图5、图6和图7中的(a)、(b)分别表示汽车在前轮转角为1°，车速分别为96 km/h、72 km/h和48 km/h时的横摆角速度时间响应曲线和质心侧偏角时间响应曲线，实线表示三自由度汽车模型(3-DOF)，虚线表示二自由度汽车模型(2-DOF)。从仿真结果中可以看出，三自由度汽车模型的响应更收敛，这是因为三自由度汽车模型考虑了车身的侧倾效应；但是与二自由度汽车模型的区别并不大，曲线趋势也大致相同，说明本文建立的三自由度汽车操纵模型是比较准确可靠的，基本可以反映出汽车的操纵特性；同时也可以看出，随着车速的提高，横摆角速度和质心侧偏角的稳态响应值逐渐变大，而且刚进入转弯行驶时的波动也变大了，说明车速越高，汽车越趋于不稳定行驶。

(a) 横摆角速度曲线 (b) 质心侧偏角曲线

(a)横摆角速度曲线 (b) 质心侧偏角曲线

(4)不同车速下三自由度汽车模型的侧倾角变化，变化曲线见图8。

图8 不同车速下3-DOF的侧倾角曲线

图8给出了三自由度汽车模型在不同车速下的侧倾角时间响应曲线，实线表示车速为96 km/h；点划线表示车速为72 km/h；虚线表示车速为48 km/h。从图8中可以看出，随着车速的提高，汽车侧倾角的瞬态响应曲线不断变陡，稳态响应值也逐渐增加，说明汽车的侧倾现象在不断加剧，这告诫人们在正常行车时，一定要注意安全，千万不能高速行驶。