多任务孪生支持向量聚类算法
2020-04-29朱文文黄成泉
朱文文, 黄成泉, 阮 丽
(1 贵州民族大学 数据科学与信息工程学院, 贵阳 550025; 2 贵州民族大学 工程技术人才实践训练中心, 贵阳 550025)
0 引 言
传统机器学习方法,如分类和聚类,是假设要处理的数据必须来自于同一分布,当要处理的数据是来自于不同分布时,传统机器学习方法需要分别对每个分布下的数据、即每个任务进行学习,这样就导致较多的时间花费,且忽略了任务间的相关性,特别是当某一任务的数据有限时,采用传统机器学习技术并不能够获得很好的效果,多任务学习正是为了应对这种情况而被提出的。
聚类在计算机视觉、文本挖掘、生物信息学和信号处理等多个领域都有应用。聚类是机器学习中最基本的方法之一,其目的是将数据点划分为簇,使得同一个簇中的数据具有较大的相似性,不同簇之间的数据具有较大的差异性。考虑到传统的基于点的聚类方法、如K-均值是根据数据集的分布将数据划分到所属集群中,当数据没有分布在多个集群点时,传统的基于点的聚类方法聚类性能很差。因此,本文在孪生支持向量聚类[1]模型基础上基于平面进行聚类。为了保持任务间的差异性、又充分利用任务间的相关性,从而整体上提高每个任务的聚类性能,本次研究把单任务孪生支持向量聚类扩展到多任务学习框架下,提出了多任务孪生支持向量聚类算法,多任务孪生支持向量聚类假设任务间共享一个公共的表示,同时学习多个相关任务,从而整体上提高所有任务的聚类性能。
1 孪生支持向量聚类
在孪生支持向量机的研究基础上,Wang等人[1]提出了孪生支持向量聚类(twin support vector clustering , TWSVC),在TWSVC中,为了寻找k个聚类中心平面ωTixi+bi=0,i=1,…,k,通过求解以下聚类模型:
(1)
其中,c>0为惩罚参数;ξi>0为松弛向量;ωi为超平面的法向量;bi为超平面的偏移量。
分析可知,式(1)为一个二次规划问题。其模型的几何意义为:第Xi个样本点在TWSVC中需要尽可能靠近第i个聚类中心平面,而远离其他类的中心平面。
通过核技巧将TWSVC扩展到非线性情况下,非线性TWSVC在一个合适的内核生成空间中寻找k个聚类中平面,即:
K(x,X)ui+γi=0,i=1,2,…,k,
(2)
其中,K(·,·)是一个适当的核函数。
非线性孪生支持向量聚类模型为:
(3)
其中,ηi(i=1,2,…,k)为松弛向量。
2 多任务孪生支持向量聚类
基于前述工作,将孪生支持向量聚类扩展到多任务学习框架下,研究认为所有的任务都有一个公共的表示[ωi;bi],[ωit;bit]表示任务t与共享的公共表示之间的偏差。多任务孪生支持向量聚类模型为:
(i=1,2,…k).
(4)

类似于TWSVC求解方法,上述优化问题可以通过凹凸过程(CCCP)[2]求解,该过程将式(4)中的第i个问题分解为一系列具有初始ω0i和b0i的凸二次子问题,此时有:
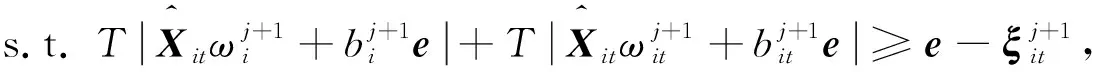
ξj+1it≥0.
(5)
其中,子问题的指数j=0,1,2,…,T(·)定义为一阶泰勒展开式。

注意到:
由此可以得到:
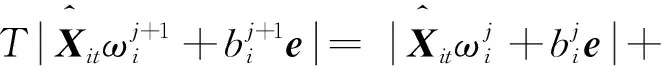
(6)
同理可得:
因此模型(4)的约束为:
(7)
从而,模型(4)等价为:

ξj+1it≥0,
(8)
受支持向量机[4-5]、孪生支持向量机[6-7]的启发,求解[ωj+1i;bj+1i]与[ωj+1it;bj+1it],通过求解(8)的对偶问题:
s.t. 0≤α≤ce,
(9)
其中,
H=[Xie],Ht=[Xite],
并且α∈R是拉格朗日乘子向量。
问题(9)是一个凸QPP问题,通过逐次超松弛[8]方法可以有效地解决,该方法是求解线性方程组的迭代方法,并成功地推广到求解上述问题[9],通过以下式子可得式(9)的解,从而得到式(8)的解:
[ωj+1i+ωj+1it;bj+1i+bj+1it]=(HTH)-1GTα+
(10)
综上,对于i=1,2,…,k,式(4)可以通过以下步骤来求解:
(1)初始化[ω0i+ω0it;b0i+b0it]。
(2)对于j=0,1,2,…,通过式(10)求[ωj+1i+ωj+1it;bj+1i+bj+1it]。
(3)如果‖[ωj+1i+ωj+1it;bj+1i+bj+1it]-[ωji+ωjit;bji+bjit]‖≤ε,停止迭代,并设置ωi=ωj+1i+ωj+1it,bi=bj+1i+bj+1it。
通过内核技巧将上面的线性多任务孪生支持向量机扩展到多任务非线性孪生支持向量机,即:
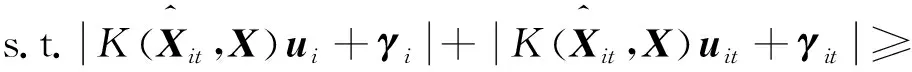
e-ηit,ηit≥0(i=1,2,…k).
(11)
其中,ηit为松弛向量,模型(11)的优化过程类似于上述线性情况的优化过程,此处不再赘述。
3 结束语
本文在孪生支持向量聚类模型上进行改进,将孪生支持向量聚类模型扩展到多任务学习框架下,提出了多任务孪生支持向量聚类算法,通过求解一系列二次规划问题确定聚类中心平面。同时学习多个相关任务的经验和理论表明,相对于独立学习每个任务,该算法利用任务间的相关性来提升所有任务的聚类性能。
