基于双未知输入扩展自校准滤波的火星大气进入段自主导航算法
2020-04-29杨海峰傅惠民
杨海峰, 傅惠民
(北京航空航天大学 小样本技术研究中心, 北京 100191)
0 引 言
火星探测是人类深空探测的热点之一,更是各航天大国展现自身综合国力和科技水平的平台。中国在顺利实施“嫦娥”系列月球探测任务之后,与火星探测相关的技术研究也正在逐步进行。不同于月球探测,火星探测任务由于地球与火星之间的距离太过遥远,无法进行实时控制,这就要求火星探测器必须具备高精确的自主导航系统。正因如此,火星探测的高精度自主导航一直都是国内外研究的前沿与热点问题[1-5]。
探测器着陆火星需经历进入、下降和着陆(Entry, Descent and Landing, EDL)过程,而火星大气进入段是最重要的阶段之一,其自主导航精度直接影响最终着陆的成功与否[6-8]。由于火星大气进入段是EDL过程中历时最长、气动环境最为恶劣的阶段,其探测器的运动状态将受到突风、沙尘暴等诸多未知因素的影响,导致其动力学特性无法精确建模[9-12];同时,惯性测量装置(Inertial Measurement Unit,IMU)存在漂移,导致量测数据中不可避免地存在未知输入(偏差)。因此,亟需建立一种能够消除上述两种未知输入影响的火星大气进入段自主导航算法。
自适应Kalman 滤波方法(Adaptive Kalman Filter)[13], 试图通过调用前N步的状态估计来修正未知输入的影响, 但这些数据往往与当前时刻的状态关系不大,有时反而会造成更大的误差,甚至导致滤波发散。为此,傅惠民等提出一种自识别自校准滤波方法[14-15],该方法能够在系统的动力学方程和量测方程均含有未知输入时,自动对其未知输入进行识别、估计和补偿,消除偏差影响,并通过数据融合减小偶然误差影响,提高滤波精度。基于这一理论,结合火星大气进入段着陆导航的工程实际,本文建立了一种新的火星大气进入段自主导航算法,该算法可以有效消除突风等未知环境因素和量测设备未知漂移的影响,大幅提升火星大气进入段自主导航的精度。
1 含双未知输入的火星大气进入段自主导航模型
火星大气进入段自主导航模型通常由动力学方程和量测方程组成,考虑到突风等不确定因素以及量测设备不精确的影响,含双未知输入的自主导航模型为:
Xk=fk-1(Xk-1)+bk-1+Wk-1,
(1)
Yk=hk(Xk)+dk+Vk,
(2)
式中,fk(·)和hk(·)均为非线性向量函数;Xk为m维状态向量,Yk为n维量测向量;bk和dk均为未知输入;Wk是方差矩阵为Qk的状态噪声向量;Vk是方差矩阵为Rk的量测噪声向量,并且满足:
(3)
1.1 含未知输入的动力学方程
式(1)中,X=(r,v,γ,θ,λ,ψ)T为探测器运动状态向量,其微分形式为[16-17]:
(4)
式中,r表示探测器质点到火星中心的距离;v表示探测器质点在火星中心固联坐标系下的速度;σ为探测器的滚转角,γ和ψ分别为航迹倾角和航向角;θ和λ分别表示探测器位置对应的火星经度和纬度;gM为火星重力加速度,D和L分别表示探测器的气动阻力加速度和升力加速度,其具体的计算公式如下所示:
(5)
(6)
(7)
其中,μ=42 828.29×109m3/s2为火星引力常数;CD与CL分别为探测器的阻力系数与升力系数;Sr为探测器参考表面积;mc为探测器质量;ρ为火星大气密度,由下式给出:
(8)
其中,ρ0=2×10-4kg/m3为火星标准大气密度;r0=3 437.2 km为距离火星表面40 km的径向基准位置;hs=7.5 km为火星大气定标高度。
由于突风、模型参数选取不当等因素的影响,在探测器运动状态的6个维度上都有可能产生未知输入,所以b一般表示为:
b=(b1,b2,b3,b4,b5,b6)T.
(9)
1.2 含未知输入的量测方程
火星探测器可基于IMU对自身加速度进行测量,进而得到探测器的运动状态;此外,探测器还可通过与已知位置信息的火星导航信标之间的无线电通讯得到自身的运动状态。因此,本文选用IMU加速度计和基于3个导航信标的无线电测距、测速的组合量测模型。
式(2)中量测向量Y的具体形式为[16,18-19]:
Y=(aTy,rTy,vTy)T,
(10)
其中,ay为加速度计在火星中心固联坐标系下的量测结果,其量测方程如下所示:
ay=CpCvav+da+Va,
(11)
式中,da=(dk,1,dk,2,dk,3)T,Va=(Vk,1,Vk,2,Vk,3)T, 而dk, j和Vk, j分别为dk和Vk的第j个分量;av为探测器在速度坐标系下的实际加速度向量;Cv是由速度坐标系到导航坐标系的转换矩阵;Cp是由导航坐标系到火星中心固联坐标系的转换矩阵,其具体形式由下式给出:
av=(-D,-Lsinφ,Lcosφ)T,
(12)
(13)
(14)
式(10)中的ry和vy分别为由无线电测距和多普勒测速得到的量测结果,其具体形式为[16,18-19]:
ry=(ry,1,ry,2,ry,3)T,
(15)
vy=(vy,1,vy,2,vy,3)T,
(16)
式中,ry, j和vy, j分别为探测器相对于第j个火星导航信标的距离和径向速度,其量测方程由下式给出:
ry, j=rc, j+dk, j+3+Vk, j+3,j=1,2,3,
(17)
vy, j=vc, j+dk, j+6+Vk, j+6,j=1,2,3,
(18)
其中,rc, j和vc, j分别为相对距离与径向速度的实际值,其计算公式为:
(19)
(20)
其中,rc和vc、rb,j和vb,j分别为探测器和第j个导航信标在火星中心固联坐标系下的位置和速度向量,前者由下式计算得到:
rc=(rcosλcosθ,rcosλsinθ,rsinλ)T,
(21)
(22)
需特别指出的是,由于量测数据中只有IMU的加速度计中存在未知输入,而无线电测距与多普勒测速只有随机误差的影响,不存在未知输入。因此,量测方程未知输入向量的9个维度中,与导航信标相关的后6个维度取值均为0,即
dk=(dk,1,dk,2,dk,3,0,0,0,0,0,0)T.
(23)
2 双未知输入自主导航滤波算法
下面对式(1)和式(2)给出的由动力学方程、IMU加速度计和基于3个导航信标的无线电测距测速组成的含双未知输入的导航模型(m=6,n=9)进一步建立其相应的导航滤波算法。
2.1 双未知输入自识别自校准
(1)状态方程未知输入自识别自校准

(24)

j=1, 2,…,m,
(25)
(26)

(2)量测方程未知输入自识别自校准

(27)

(28)
(29)

2.2 双未知输入自主导航滤波
(1)一步自校准预测
Xk=Φk-1Xk-1+UX,k-1+bk-1+Wk-1,
(30)
其中,
(31)
(32)
非线性系统一步自校准预测为:
(33)
一步预测误差协方差矩阵Pk/(k-1)为:
Pk/(k-1)=Φk-1Pk-1ΦTk-1+Qk-1+Ωk-1+ΩTk-1+Ω*k-1,
(34)
其中,
Ωk-1=Φk-1[Pk-1-Sk-1ΦTk-2-(I-Kk-1Hk-1)Qk-2]T*k-1,
(35)
Ω*k-1=T*k-1[Pk-1+Φk-2Pk-2ΦTk-2+Qk-2-Sk-1ΦTk-2-
(I-Kk-1Hk-1)Qk-2-Φk-2STk-1-QTk-2(I-Kk-1Hk-1)T]T*k-1,
(36)

Sk-1=(I-Kk-1Hk-1){Φk-2Pk-2+T*k-2[Pk-2-Φk-3STk-2-
QTk-3(I-Kk-2Hk-2)T]}+Kk-1Tk-1(Hk-2Pk-2-RTk-2KTk-2),
(37)
S2=(I-K2H2)Φ1P1,
(38)
对于k=1,2的情况,系统一步预测为:
(39)
一步预测误差协方差矩阵Pk/(k-1)为:
Pk/(k-1)=Φk-1Pk-1ΦTk-1+Qk-1,
(40)
滤波初始化为:
(41)
(42)
(2)量测自校准估计
Yk=HkXk+UY,k+dk+Vk,
(43)
式中,
(44)
(45)
(46)
量测估计误差协方差矩阵PY, k为:
PY, k=HkPk/(k-1)HTk+Rk+HkΨk+ΨTHTk+Ψ*k,
(47)
其中,
Ψk=-{Φk-1Pk-1HTk-1+T*k-1[Pk-1-Φk-2STk-1-QTk-2(I-
Kk-1Hk-1)T]HTk-1-Φk-1Kk-1Rk-1-T*k-1Kk-1Rk-1}Tk,
(48)
Ψ*k=Tk(Hk-1Pk-1HTk-1+Rk-1-Hk-1Kk-1Rk-1-RTk-1KTk-1HTk-1)Tk,
(49)

对于k= 1,2的情况,量测估计为:
(52)
量测估计误差协方差矩阵PY, k为:
PY, k=HkPk/(k-1)HTk+Rk,
(51)
(3)状态估计
(52)
状态估计误差协方差矩阵Pk为:
Pk=Pk/(k-1)-KkPTXY, k,
(53)
其中,Kk为滤波增益矩阵,由下式计算得到
Kk=PXY, kP-1Y, k,
(54)
PXY, k=Pk/(k-1)HTk+Ψk.
(55)
式中,Ψ1=Ψ2=0。
3 算例对比与结果分析
采用美国火星科学实验室(Mars Science Laboratory, MSL)任务中好奇号(Curiosity)着陆探测器在大气进入段的实际数据[11,16],分别对本文算法和基于EKF的自主导航算法进行500次独立数字仿真,并将状态各维度上的均方根误差(RMSE)作为评价导航性能的指标。
火星探测器的初始运动状态和状态估计见表1,3个火星导航信标的分布情况见表2。

表1 探测器初始运动状态及其估计

表2 火星导航信标分布
火星大气进入段导航持续时间300 s,取相邻两步之间的时间间隔为1 s,设动力学方程和量测方程中的未知输入bk-1和dk分别为:
(56)
dk=(0.003,0.003,0.003,0,0,0,0,0,0)T, 1≤k≤300.
(57)
500次蒙特卡洛仿真所得两种算法在各维度上均方根误差对比情况如图1所示,均方根误差均值的对比见表3。

表3 本文算法与EKF导航算法的RMSE均值比较
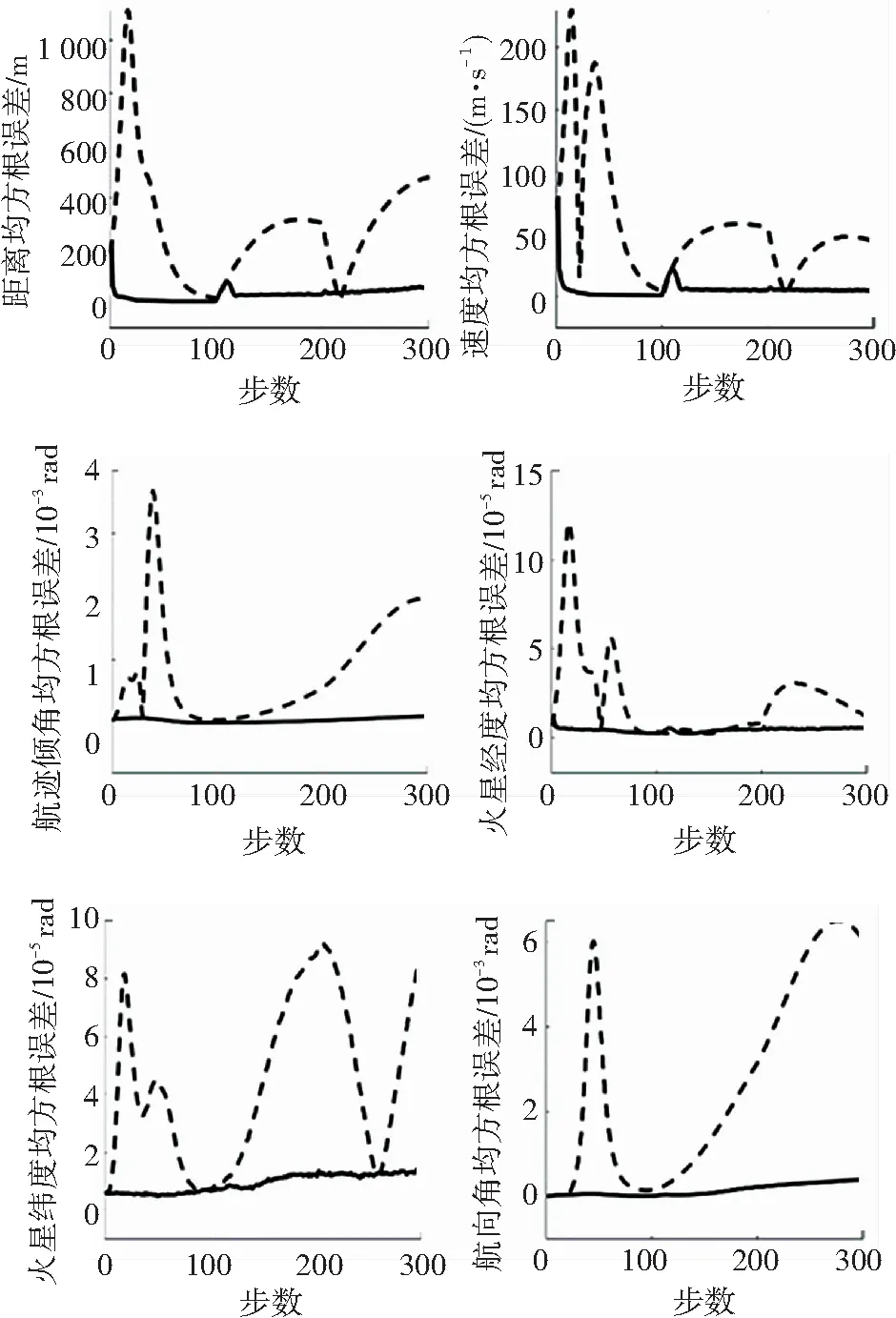
图1 本文算法(实线)与EKF导航算法(虚线)的状态估计RMSE比较
Fig. 1 State estimationRMSEscomparison of the proposed algorithm and the EKF navigation algorithm
由图1和表3中的计算结果可以看出,当着陆探测器在大气进入段受到突风等不确定因素影响且加速度计存在未知漂移时,本文算法可以很好地消除这些未知输入的影响,状态估计误差远小于基于EKF的自主导航算法,且导航全程估计结果都保持稳定,具有很强的鲁棒性。
4 结束语
为进一步提升火星大气进入段自主导航精度,消除动力学模型中突风、沙尘暴以及量测模型中IMU漂移等未知输入对探测器运动状态估计的影响,本文将双未知输入扩展自校准滤波引入火星自主导航工程实际中,建立了一种新的火星大气进入段自主导航算法。大量计算结果表明,与传统算法相比,本文算法导航精度更高,鲁棒性更强,能更好地满足未来火星高精度定点着陆的需求。
