用表格法分析数量关系解决问题
2020-04-28茅莉萍
茅莉萍

方程是解决实际问题中“数量相等关系”的有效模型。利用方程知识解决实际问题的关键是从研究问题中的数量关系人手,将问题中的已知量与未知量之间的数量关系找出来,通过适当设元,进而建立方程。在七年级上册“用一元一次方程解决问题”中,教材结合具體例题介绍了表格法、线形示意图法、圆形示意图法、柱状示意图法等常见的数量关系分析法。其中表格法能够使问题中复杂的数量关系变得简单明了,因此其应用也最为广泛,在七年级下册“用二元一次方程组解决问题”,八年级下册“分式方程”,九年级上册“用一元二次方程解决问题”中均又出现用表格法进行数量关系分析的例题,可见,表格法是解决实际问题非常有用的方法之一。
例1 (2019·安徽)为实施乡村振兴战略,解决某山区老百姓出行难的问题,当地政府决定修建一条高速公路。其中一段长为146米的山体隧道贯穿工程由甲乙两个工程队负责施工。甲工程队独立工作2天后,乙工程队加入,两工程队又联合工作了l天,这3天共掘进26米。已知甲工程队每天比乙工程队多掘进2米,按此速度完成这项隧道贯穿工程,甲乙两个工程队还需联合工作多少天?
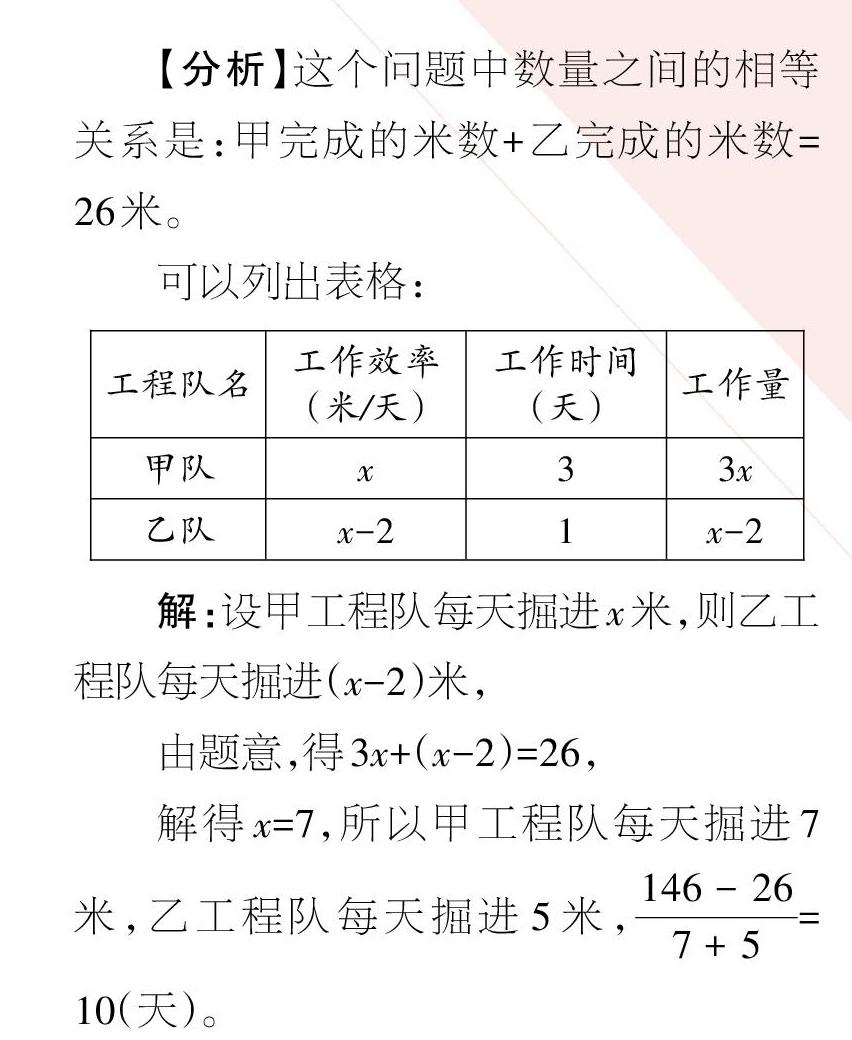
【分析】这个问题中数量之间的相等关系是:甲完成的米数+乙完成的米数=26米。
可以列出表格:
解:设甲工程队每天掘进x米,则乙工程队每天掘进(x-2)米,
由题意,得3x+(x-2)=26,
解得x=7,所以甲工程队每天掘进7米,乙工程队每天掘进5米,
10(天)。
答:甲乙两个工程队还需联合工作10天。
【点评】本题涉及的是两个队的工作效率、工作时间、工作量这三个量之间的数量关系。可以利用“工作效率×工作时间=工作量”这个关系辅助列表,分析数量关系,利用一元一次方程解决问题。本题还可以利用“前两天的工作量+后一天的工作量=26米”来列表分析。
例2 (2019·辽宁朝阳)佳佳文具店购进A、B两种款式的笔袋,其中A种笔袋的单价比B种笔袋的单价低10%。已知店主购进A种笔袋用了810元,购进B种笔袋用了600元,且所购进的A种笔袋的数量比B种笔袋多20个。请问:文具店购进A、B两种款式的笔袋各多少个?
【分析】这个问题中数量之间的相等关系是:A种笔袋的单价=B种笔袋的单价×(1-10%)。
可以列出表格:
解:设文具店购进B种款式的笔袋x个,则购进A种款式的笔袋(x+20)个,
依题意,得:810—600(1-10%),解
得:x=40,
经检验,x=40是所列分式方程的解,且符合题意,∴x+20=60。
答:文具店购进A种款式的笔袋60个,B种款式的笔袋40个。
【点评】本题涉及的是两个款式的单价、数量、总价这三个量之间的数量关系。可以利用“单价=总价÷数量”这个关系辅助列表,分析数量关系,利用分式方程解决问题。本题还可以利用“数量=总价÷单价”来列表分析解决。
例3 (2019·四川宜宾)某产品每件的生产成本为50元,原定销售价65元,经市场预测,从现在开始的第一季度销售价格将下降10%,第二季度又将回升5%。若要使半年以后的销售利润不变,设每个季度平均降低成本的百分率为x,根据题意可列方程为________。
【分析】这个问题中数量之间的相等关系是:变化前利润=变化后利润。
可以列出表格:
解:设每个季度平均降低成本的百分率为x,
依题意,得:65x(1-10%)x(1+5%)-50.(1-x)2=65 -50。
【点评】本题涉及的是变化前后的售价、成本价、利润三个量之间的数量关系。可以利用“售价一成本价=利润”这个关系辅助列表,分析数量关系,利用一元二次方程解决问题。
由以上的几个例题我们可以看到,表格分析法是一种有效的分析数量关系的方法,其主要针对两种情况(如A款、B款;变化前、变化后……),含有三个关联量(如售价、成本价、利润……)的问题,这样的问题在现实生活中大量存在。对以上三例的解法步骤进行归纳,我们就可以得出用表格法分析数据解决问题的基本步骤:一是采用三行四列制表格;二是把题目中的已知量填写进表中;三是设好未知数,由三个量的基本关系,用含有未知数的代数式表示出表中剩下的量;四是根据题目条件中寻找到的等量关系列出方程,解决问题。
(作者单位:江苏省无锡市侨谊实验中学)
