不同因素影响下层状土壤水分入渗特征及水力学参数估计*

马蒙蒙，林 青，徐绍辉

不同因素影响下层状土壤水分入渗特征及水力学参数估计*

马蒙蒙，林 青，徐绍辉†

（青岛大学环境科学与工程学院，山东青岛 266071）

层状土壤是自然界常见的土体结构，其水分运移规律不同于均质土；大气降水、灌溉水等水分的入渗是土壤水文过程的一个重要环节，同时它也与地下水补给、污染物运移等过程紧密相关。土壤初始含水量、土体构型及供水强度等因素均会影响水分的入渗过程。为探究积水深度、土体构型、初始含水量三种因素对层状土壤水分运移的影响，通过室内积水入渗试验对湿润锋、累积入渗量、土壤剖面压力水头进行观测，并利用Hydrus-1D模型反演水力参数并对相应条件下的水分运移规律进行模拟和分析。结果表明，层状土壤中湿润锋随时间的推进方式由非线性过渡至线性，入渗率逐渐减小。三种因素作用下，层状土壤水分运移特征有明显差异：积水深度、土壤初始含水量增加时，湿润锋运移速率和入渗率均增大，且各观测点压力水头升高加快，土壤不饱和程度降低；上砂壤下粉砂壤构型较上粉砂壤下砂壤构型而言，整体湿润锋推进速率和入渗率较大，出流快，且入渗后期界面处的压力水头高于其他观测点。且结果表明，反演的水力学参数较拟合实测的参数更适用于层状土壤入渗的模拟和预测。该研究旨在揭示和掌握层状土壤水分运移规律和影响因素的作用机制，并进一步为农田灌溉措施的合理制定提供科学依据。

层状土壤；土体构型；积水深度；初始含水量；Hydrus-1D

因地质沉积、水文过程及耕作等活动，田间土壤多呈层状结构，这种结构对水分入渗及污染物的运移具有强烈影响。早有研究表明水分在均质土和层状土中的运移规律有很大差异[1]。基于均质土入渗理论，国内外学者对多种条件下层状土壤的入渗过程进行了大量试验和理论研究[2-6]。由于土壤本身的结构和特性，以及供水方式和降雨强度等诸多因素均会影响水分的运移，学者们从多个角度对影响水分运移的因素进行了详细的讨论。Si等[7]发现，土体构型（Soil configuration）对水分运动产生影响主要是由于土体中的异质层造成的水流阻滞效应，使得分层界面处的土壤孔隙和水力学性质出现明显的不连续，从而影响整个土体内的水流通量和含水量分布[8]。李毅等[9]通过对湿润锋、累积入渗量和剖面含水量的观测发现，夹层位置和土壤质地变化对层状土壤入渗规律有明显影响。范严伟等[10]基于Hydrus-1D软件模拟了不同砂层质地、埋深、厚度及压力水头和初始含水率条件下的水分入渗过程，结果表明土壤剖面含水率主要受砂层质地、埋深和砂层厚度的控制。刘汗等[11]采用径流-出流法和双环入渗法对比测量入渗率，分析了土壤入渗性能对初始含水率和降雨强度的响应，结果表明：入渗能力随着降雨强度的增加而降低，随着初始含水率的增加而降低。总之，现有研究已涉及了土壤质地、容重、初始含水量等因素对土壤水分运移特征的影响，但由于层状土体构型和试验自身设计等条件的不同，导致一些类似研究结果有所差异。深入研究土壤水分入渗及再分布等运移规律问题，对增加土壤储水量、减少土壤水渗漏有重要意义。但以往的研究多是以湿润锋和累积入渗量为观测指标分析水分的入渗特征，对运移过程中剖面含水量及压力水头的观测和分析较少。

本文通过层状土壤积水入渗试验并基于Hy- drus-1D软件，以湿润锋、累积入渗量、压力水头为观测指标，分别探讨了不同积水深度、土壤初始含水量、土体构型下的层状土壤水分运移规律，以便深入了解层状土壤水分运动过程，为优化田间水分管理提供依据。因考虑到土层界面的影响，直接利用层状土壤剖面观测数据反演水力参数（并非均质土分开反演），同时对比直接拟合的水力参数，分析两种方法所得参数的适用性。

1 材料与方法

1.1 供试材料

供试土样取自青岛市平度南村镇农田，去除表层10 cm土壤后，剖面10～100 cm按土壤质地类型大致分为两层：10～40 cm、40～100 cm。采用环刀取剖面30、60 cm处的原状土，用于Ku-pF非饱和导水率测量系统测定土壤水分特征曲线；取一定量扰动土样经风干、碾压、过2 mm筛备用；同时对土样进行基本理化性质测定，见表1。

表1 供试土壤的理化性质

1.2 试验方法

试验采用马氏瓶供水，马氏瓶和试验土柱均为有机玻璃材质（外壁贴有刻度尺）。其中马氏瓶内径10 cm，高100 cm；土柱内径15 cm，高60 cm，且土柱侧壁有六个孔供安装土壤水势传感器（TS-2型水势传感器，中国科学院南京土壤研究所），顶部设进水口，底部设出水口。

图1 层状土传感器布置图（A：粉砂壤土；B：砂质壤土。图中单位：cm）

试验步骤：装填完成后，调整马氏瓶位置及内管高度，在土壤表面加入与设计积水深度等量的水，保证在定水头情况下开始入渗；试验过程中记录不同时刻湿润锋位置、马氏瓶读数和水势传感器读数；当出水口有水流出时，停止供水，结束试验，并快速抽出表层积水，进入土壤水再分布状态。

本文具体试验设计见表2（共6组试验），其中土壤初始含水量中前两组W1、W2是通过将土样风干至不同程度获得；W3是经积水入渗及再分布后的土柱中较高含水量的土样，其含水量值通过土壤水分特征曲线计算测定。

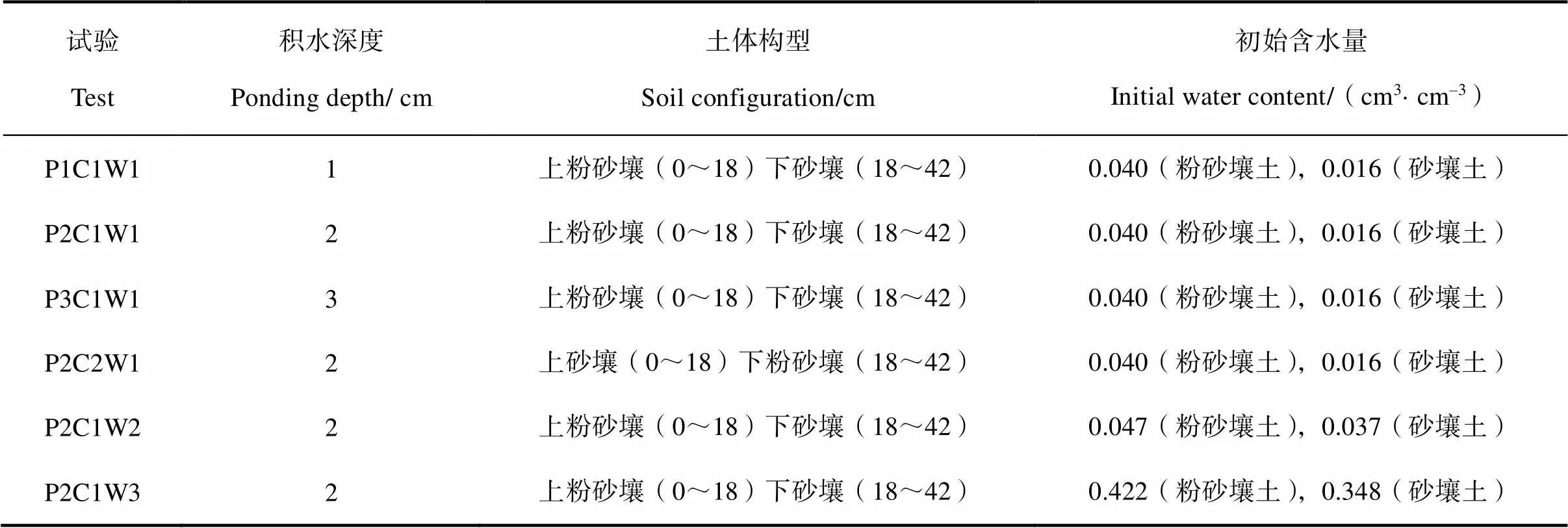
表2 试验方案

注：P代表积水深度，C代表土体构型，W代表初始含水量。Note：P stands for depth of ponding water；C for soil configuration；W for initial water content.

1.3 数值模型

假设土壤为各向同性均质介质，可通过一维非饱和土壤水运动方程[12]（the Richards Equation）和定解条件进行数值模拟。在Hydrus-1D 软件中，可通过控制初始条件和边界条件，基于正演模块和反演模块，形成能完整描述水流运动的数学模型，其方程、初始条件和边界条件分别为:

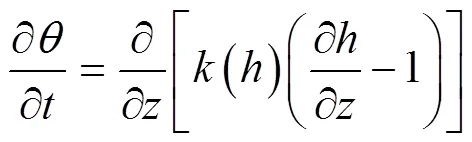
入渗过程中定压力水头为模型的上边界，自由排水作为模型的下边界。

初始条件：

上边界：

下边界：

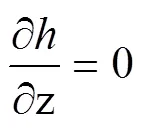
式中，为体积含水量（cm3·cm–3），为时间（min），为土壤深度（cm），向下为正；为压力水头（cm），为土壤非饱和导水率（cm·min–1），0为初始压力水头（cm），1为上边界定压力水头2（cm）。土壤水分特征曲线（）和非饱和导水率（）采用van Genuchten（VG）模型拟合[13]。

1.4 求解水力学参数

土壤水力学参数是利用数学模型分析土壤水运动特征的基本参数，即定量了解土壤水运动的基础[14]。目前常用来描述土壤水运动的VG模型中的参数为：饱和含水量（s）、残余含水量（r）、饱和导水率（s）、进气吸力倒数（）、孔隙尺寸分布指数（）。本文通过两种方法估计水力学参数，一种是利用积水入渗试验（P2C1W1）下实测的土壤压力水头-时间数据（选取中间4个观测点），运用Hydrus-1D的Inverse[15]模块对水力参数（、、s）进行反演，并对参数进行优化；其中模拟土层深度为42 cm，空间步长设为0.5 cm，模拟历时4 000 min，设置与试验中相同位置的观测点。另一种是利用Ku-pF装置测量填装土和原状土的压力水头-土壤含水量数据，通过RETC软件基于VG模型拟合获得“实测”的水力参数（s、r、；原状土、填装土）。其中两种方法下，s、r均采用实测值；s分别利用定水头法实测和反演获得。最后分别运用反演优化的参数和拟合“实测”填装土的参数对3 cm积水深度（P3C1W1）下层状土壤一维垂直入渗进行模拟，并将实测值与模拟值进行拟合、分析，从而验证参数的有效性。

2 结果与讨论

2.1 积水深度对层状土壤水分运移的影响

对比不同积水深度的试验（P1C1W1、P2C1W1、P3C1W1），图2a）反映了湿润锋的推进过程,曲线斜率dd表示湿润锋运移速率，虚线代表湿润锋到达土壤分层界面（时间分别为600、480、480 min）；图2b）表示累积入渗量的变化规律，dd表示入渗速率。图中可看出同一积水深度下：入渗前期，入渗率快且迅速减小，湿润锋运移距离和累积入渗量随时间呈非线性增长；湿润锋在到达界面后，随时间呈线性增长，运移速率基本稳定，但入渗率仍逐渐减小。随积水深度增加，湿润锋运移加快（到达界面的时间缩短），相同时间内累积入渗量也增大，但2 cm和3 cm积水深度下差异较小。

为定量分析积水深度对锋速和入渗率的影响，根据湿润锋运移特征和土壤分层状况，将湿润锋在到达分层界面前的过程，称为第一阶段，在界面下称为第二阶段[16]。由第一阶段湿润锋运移距离和时间曲线（）呈非线性增长，用幂函数进行拟合，第二阶段明显转为线性增长，故采用线性函数进行拟合，决定系数2均大于0.99，拟合效果良好。同样对整个入渗过程的累积入渗量和时间曲线（）采用幂函数拟合（因曲线分两阶段拟合的效果较整体拟合效果差，故采用整个入渗过程拟合），详见表3。

图2 不同积水深度试验下湿润锋位置和累积入渗量的变化趋势

表3 不同积水深度试验下的Z-t、I-t拟合结果

注：a、b、c、d表示拟合参数；2表示决定系数，RMSE表示均方根误差；k、α分别表示入渗系数和入渗指数Note：a，b，c and d all stand for fitting parameters；2for coefficient of determination，RMSE for root mean square error；k andαfor infiltration coefficient and infiltration index，respectively

同一积水深度下，第一阶段入渗率随时间迅速减小（如2 cm积水深度下，入渗率由1 min时的4.2 cm·min–1降至10 min的0.42 cm·min–1），主要是由于入渗初期土体较干燥,入渗能力较强，随着水分入渗，土壤含水量不断增长，水吸力减小，故锋速和入渗率由快变慢；第二阶段湿润锋推进速度为定值（值）。锋速、入渗率随积水深度增加而增大，这与之前的研究结果相似[17]，主要是因为积水深度增加，入渗界面处压力势增大，利于水分下渗。但由于上层土壤黏粒含量较高，水分运移慢，或由于上层土壤因积水压力的压实作用导致入渗界面土壤结构发生变化，土壤密度变大[18]，入渗速率较小。积水深度为2 cm和3 cm时的入渗率差异很小，分析是由于上层土壤渗透性差，供水强度远大于入渗能力，所以对入渗过程的影响差别不大，当然也不乏测量误差的原因。

图3为压力水头随时间的变化规律，各积水深度（1、2、3 cm）试验出流时间分别为4 920、4 020、4 070 min。从图中可以看出，由上至下各观测点处的压力水头依次骤升并逐渐趋于平稳。随积水深度增大，压力水头开始变化的时间提前。上层土同一时间相同观测点处压力水头随积水深度增加而增大，即含水量增大，如600 min时，1 cm和3 cm积水下上层土壤近界面处的观测点（17 cm处）的压力水头分别为–136 cm、–102 cm，积水深度的变化对入渗通量有直接影响[19]。下层砂壤土受表面积水影响较小，随着上层土壤逐渐趋于饱和，聚集于界面的水分开始下渗，下层土壤的入渗量逐渐缓慢增加，达到田间持水量后开始渗漏出流。

2.2 土体构型对层状土壤水分运移的影响

土体构型即土壤的结构形态，是构成土壤剖面特征土层的排列形式[20]，影响着土壤水流及溶质的运移。由图4可看出其对湿润锋运移和入渗能力具有明显的影响，两种构型下湿润锋到达界面的时间分别为60、480 min，差异明显。由图4a）明显看出当土体构型为上砂壤下粉砂壤时，在湿润锋穿过界面后，湿润锋的运移速度（斜率）快速并持续降低（锋速由50 min时0.20 cm·min–1降至70 min时的0.14 cm·min–1），由非匀速推进转变为匀速推进；而当土体构型为上粉砂壤下砂壤时，湿润锋速度缓慢减小，到达界面后未呈现出明显变化（湿润锋到达界面前后，锋速均保持在0.02 cm·min–1左右），同样匀速推进；且前一构型下锋速远大于后者。由图4b）可看出上砂下粉构型的累积入渗量明显大于另一构型且差值逐渐增大，两构型均表现为入渗率随时间逐渐减小，且湿润锋到达界面处的入渗率分别为0.20、0.021 cm·min–1。

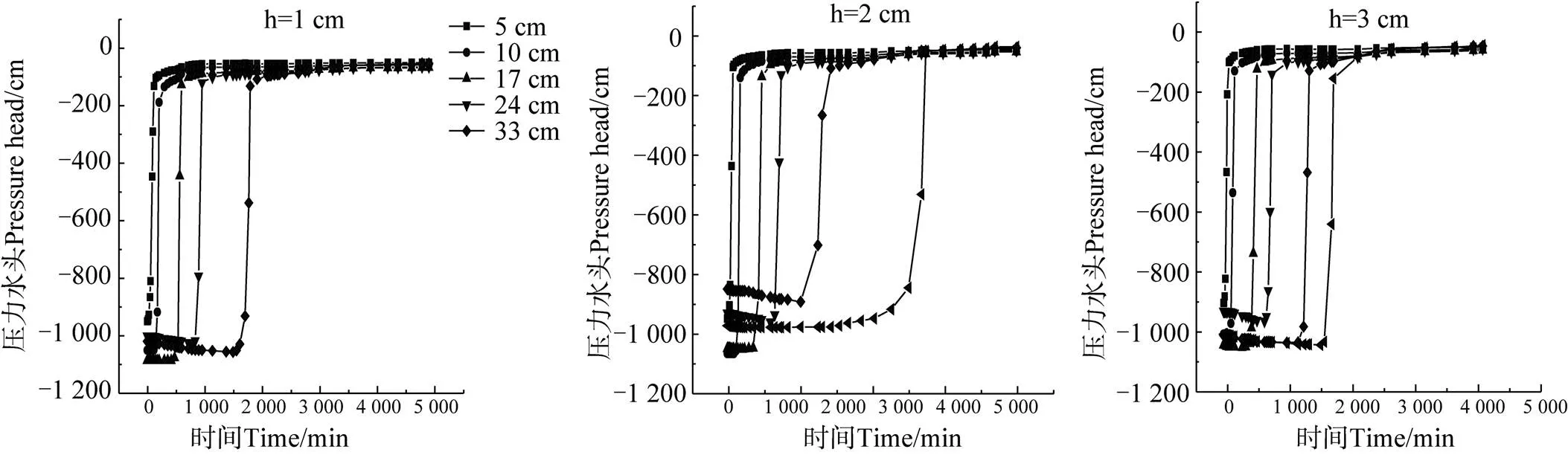
图3 不同积水深度试验下层状土壤不同深度处的压力水头随时间的变化

研究表明层状土壤入渗率与上层土壤饱和导水率和下层土壤进水吸力有关。由图4可知在上粉下砂型土壤中锋速和入渗率均低于上砂下粉构型，分析主要是在上粉下砂构型中，其上层土壤黏粒含量较高，导水率小，水力阻滞作用明显，严重阻碍了水分向下运移；而且当湿润锋到达界面后，湿润锋处的基质势足够小，它会阻碍下层粗质土中大量大孔隙的入渗[21]，从而降低了下层土壤入渗能力，使得锋速和入渗率明显小于上砂下粉型。

由图5 a1）、图5b1）可知，两土体构型入渗试验的出流时间分别为4 020、1 920 min，从上到下各观测点压力水头依次骤升并趋于平稳，并且急剧上升的时刻与湿润锋经过的时刻相近，这与先前王春颖等[22]的研究相一致。相比上粉下砂构型，上砂下粉构型试验中各观测点处压力水头开始上升时间提前、变化更快，且出流快。入渗后期两种构型均为上层压力水头略高于下层，最终趋于稳定；但不同的是砂壤在上时，近界面位置（17 cm处）观测点处的压力水头略高于其他观测点处的压力水头。图5a2）、图5b2）是两种构型下水分再分布过程中压力水头的变化规律，其中上粉下砂构型：上层土壤的3个位置处的压力水头在入渗结束后快速下降，位置越靠上，下降幅度越大；下层3个位置处的压力水头开始缓慢波动，基本平稳不变，后期缓慢下降，最终各位置压力水头值一直在上下波动。上砂壤下粉砂壤构型中：前期上层压力水头快速下降，下层压力水头缓慢下降，但后期各观测点压力水头波动很小，基本平稳不变。

图4 不同土体构型试验下湿润锋位置和累积入渗量的变化趋势

注：a1），a2）分别表示上粉壤下砂壤型的水分入渗过程和水分再分布过程；b1），b2）分别表示上砂壤下粉壤的水分入渗过程和水分再分布过程 Note：a1）and a2）stands for water infiltration and water redistribution processes in the sandy loam covered with silt loam，respectively；and b1），b2）for water infiltration and water redistribution processes of silt loam covered with sandy loam，respectively

上粉下砂构型水分整体运移速度远小于其他构型，主要是因为上层粉砂壤较强的阻渗作用，而且水力阻滞会因含水量的增加使土层界面间导水能力差异增大而愈加明显[23]。上砂下粉构型出流快说明土体易渗漏。入渗后期上层土壤更先接近饱和状态，故上层土壤压力水头高于下层土壤。界面上方观测点处压力水头略高是因为下层土壤的阻水作用，使水分在界面上聚积，进而提高了上层土壤的蓄水能力[24]。水分再分布过程中，土壤上界面无积水压力的作用，故水分仅在重力和基质势的作用下运动，重力作用占主导地位。上层土壤自下向上失水速度加快，上层土壤水分在重力作用下下渗，含水率（压力水头）减小，基质势降低；当基质势降低至一定程度后，下层土壤水分便克服重力在基质吸力的作用下沿毛管向上运移，补充水分的缺失，故压力水头上下波动[25]。上砂下粉构型下层土壤基质势梯度小，水分运移减缓，加上土柱底层的阻水作用，土壤含水率变化幅度很小，故压力水头平稳不变。

2.3 初始含水量对层状土壤水分运移的影响

初始含水量是田间土壤入渗能力的重要影响因素[26]。图6所示初始含水量对湿润锋和累积入渗量的影响，高、低0下湿润锋到达土壤分层界面的时间分别为330、480 min。可明显看出相同入渗时间内，初始含水量越高，湿润锋运移越快，累积入渗量越多。在接近饱和状态作为初始含水量的试验中，湿润锋不易观察，故未列出，截止出流4 h累积入渗量仅为4 cm。

图6 不同初始含水量试验下湿润锋位置和累积入渗量的变化趋势

湿润锋的运移速率随初始含水量的增大而增大，这与其他学者的研究结论一致[27]，主要是土壤持水能力有限，初始含水量增加时，所吸持的水量相应降低，有利于湿润锋向下运移。累积入渗量和入渗率随着初始含水量的增加而增大，这与曾辰等[28]、张向炎等[29]、Malik等[30]的研究结果不同，但与王全九等[31]和刘目兴等[32]的研究结果一致。土壤初始含水量越低，一方面与含水量直接相关的基质势越高，增大了湿润峰前端的水吸力，利于水分入渗；另一方面也增强了土壤团聚体遇水后的崩解挤压作用，降低孔隙度，进一步减缓下渗[33-34]。两方面共同作用，致使试验结果有所差异。接近饱和时水分的入渗基本达到稳渗状态，相较干燥土壤，吸水后团聚体膨胀、孔隙减少，故入渗率远低于干燥土，这也是间歇降雨中，后期降雨入渗率远低于初次降雨入渗率的原因[35]。

图7为不同0下压力水头的变化情况，土壤在低、高0下，试验出流时间分别为4 020、2 640 min；从图中可观察到各位置由上至下压力水头开始变化的时间分别为10、100、300、600、1 020、1 500；5、80、240、480、720、1 020 min，且入渗结束时同一时间相同观测点处压力水头值随初始含水量的增加而稍有升高。土壤初始含水量越高，虽然水势梯度减小导致入渗能力降低，但土壤的持水能力变小，土壤易饱和，利于水分下渗。在本研究中，后者作用强于前者，故0增大时，水分运移加快，故相同时间同一位置处含水量增大。

2.4 Hydrus-1D模型模拟

通过Hydrus-1D模拟土柱入渗试验（P2C1W1），反演得到层状土壤的水力学参数；利用Ku-pF测定的实验数据并结合RETC软件，拟合获得“实测”的填装土和原状土的水力学参数，见表4。

注：a）所示体积含水量为：粉砂壤0.040，砂壤0.016；b）所示体积含水量为：粉砂壤0.047，砂壤0.037 Note：a）indicates that θ0 is 0.040 in Silt loam，and 0.016 in Sandy loam；b）indicates that θ0 is 0.047 in Silt loam and 0.037 in Sandy loam（cm3·cm–3）

表4 土壤水力学参数的优化值与拟合值

分别利用表4中反演优化的参数和填装土拟合实测的参数，模拟3 cm积水深度下压力水头的变化规律，并将实测值和模拟值进行比较。图8为基于反演参数下的模拟结果：压力水头模拟值与实测值拟合效果较好，基本与实测值的变化趋势相吻合，2为0.952，RMSE为0.027。而RETC拟合的填装土的参数模拟效果较差（故未列出拟合曲线），其主要是原因是，由Ku-pF装置测定的土壤水分特征曲线是一“脱湿”过程，而用来反演参数的数据是通过土柱入渗的“吸湿”过程获得的，两者之间存在滞后现象；此外s实测值是利用定水头法（环刀）测定，与反演值相差较大，这与环刀和土柱尺寸差异较大有关。因此说明反演、优化的参数更适用于室内层状土壤入渗规律的模拟与预测。

图8 压力水头模拟值与实测值的拟合

此外，由表4可以看出由RETC拟合“实测”得到的原状土和填装土的水力参数差异较大，使得水分特征曲线有明显差异，见图9。填装土的饱和含水量和低吸力段的含水量均明显高于原状土，且填装土的水分特征曲线要较原状土陡。分析原因，可能是填装土的研磨及装填的容重差异导致土壤团聚体被破坏、改变了土壤的孔隙分布，而土壤水分特征曲线实际反映的是孔隙状况和含水量的关系[21]，故原状土和扰动土的水分特征曲线有明显差异。

图9 原状土和扰动土的土壤水分特征曲线

3 结 论

在层状土壤积水入渗试验中，湿润锋在到达土层界面后由非线性推进转为线性推进，入渗率随时间延长逐渐减小。其中上砂壤下粉砂壤构型中，湿润锋的运移速度快速并持续降低，锋速由50 min时的0.20 cm·min–1降至70 min时的0.14 cm·min–1；上粉砂壤下砂壤构型中，湿润锋速度缓慢减小，在到达界面前后，锋速均保持在0.02 cm·min–1左右；两构型下湿润锋到达界面时，入渗率分别为0.20、0.021 cm·min–1。积水深度、土体构型及初始含水量对水分运移的影响作用机制不同。积水深度主要通过影响入渗界面处的压力势来影响水分的运移过程，对入渗通量有着直接作用；土体构型对水分运移的影响主要是因剖面中不同质地土壤的孔隙、黏粒含量等差异导致渗透性、持水能力不同，且造成土层突变界面产生水力阻滞作用。土壤初始含水量对入渗的影响是通过两方面共同作用的，即与土壤含水量直接相关的水势梯度的作用和间接相关的土壤团聚体遇水后的崩解挤压作用。故可适当调整这三种因素减小土壤渗漏量，以优化田间水分管理。利用Hydrus-1D软件反演、优化的参数较RETC拟合的“实测”参数更适用于室内层状土壤积水入渗特征的模拟与预测。

［1］ Miller D E，Gardner W H. Water infiltration into stratified soil. Soil Science Society of America Journal，1962，26（2）：115—119.

［2］ Yang H，Rahardjo H，Leong E C. Behavior of unsaturated layered soil columns during infiltration. Journal of Hydrologic Engineering，2006，11（4）：329—337.

［3］ Brunone B，Ferrante M，Romano N，et al. Numerical simulations of one-dimensional infiltration into layered soils with the richards equation using different estimates of the interlayer conductivity. Vadose Zone Journal，2003，2（2）：193—200.

［4］ Huang M B，Bruch P G，Barbour S L. Evaporation and water redistribution in layered unsaturated soil profiles. Vadose Zone Journal，2013，12（1）：1—14.

［5］ Ren L D，Huang M B. Experiment and numerical simulation of soil evaporation from layered sandy soil columns. Acta Pedologica Sinica，2014，51（6）：1282—1289. [任利东，黄明斌. 砂性层状土柱蒸发过程实验与数值模拟. 土壤学报，2014，51（6）：1282—1289.]

［6］ Wu Q F，Fan J，Yang X L，et al. Experiment and simulation of infiltration from layered soils in open pit mine in Jin-Shaan-Meng adjacent region. Acta Pedologica Sinica，2015，52（6）：1280—1290. [吴奇凡，樊军，杨晓莉，等. 晋陕蒙接壤区露天矿层状土壤水分入渗特征与模拟. 土壤学报，2015，52（6）：1280—1290.]

［7］ Si B，Dyck M，Parkin G. Flow and transport in layered soils. Canadian Journal of Soil Science，2011，91（2）：127—132.

［8］ Li X P，Chang S X，Salifu K F. Soil texture and layering effects on water and salt dynamics in the presence of a water table：A review. Environmental Reviews，2014，22（1）：41—50.

［9］ Li Y，Ren X，Horton R. Influence of various soil textures and layer positions on infiltration characteristics of layered soils. Journal of Drainage and Irrigation Machinery Engineering，2012，30（4）：485—490.[李毅，任鑫，Horton Robert. 不同质地和夹层位置对层状土入渗规律的影响. 排灌机械工程学报，2012，30（4）：485—490.]

［10］ Fan Y W，Huang N，Ma X Y，et al. Simulation of infiltration characteristics in soil with sand interlayer using HYDRUS-1D. Soils，2016，48（1）：193—200.[范严伟，黄宁，马孝义，等. 应用HYDRUS-1D模拟砂质夹层土壤入渗特性. 土壤，2016，48（1）：193—200.]

［11］ Liu H，Lei T W，Zhao J. Effects of initial soil water content and rainfall intensity on loess infiltration capacity.Science of Soil and Water Conservation，2009，7（2）：1—6. [刘汗，雷廷武，赵军. 土壤初始含水率和降雨强度对黏黄土入渗性能的影响. 中国水土保持科学，2009，7（2）：1—6.]

［12］ Richards L A. Capillary conduction of liquids through porous mediums. Physic，1931，1（5）：318—333.

［13］ van Genuchten M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Science Society of America Journal，1980，44（5）：892—898.

［14］ Liu J J，Wang Q J，Wang W H，et al. Inverse solution soil hydraulic parameters and verification using Hydrus-1D model. World Sci-Tech Research & Development，2010，32（2）：173—175. [刘建军，王全九，王卫华，等. 利用Hydrus-1D反推土壤水力参数方法分析. 世界科技研究与发展，2010，32（2）：173—175.]

［15］ Šimůnek J，Sejna M，van GenuchtenM T. The HYDRUS-1D software package for simulating the one-dimensional movement of water，heat，and multiple solutes in variable-saturated media. Version4.0，Department of Environmental Sciences，University of California Riverside，USA，2008.

［16］ Lu X Y，Wei X P，Qiu Y，et al. Experimental analysis on the infiltration reduction rule by clay interlayer in sand. Journal of Water Resources and Water Engineering，2009，20（2）：22—25. [卢修元，魏新平，邱玥，等. 粉粘土夹层对砂的减渗规律试验分析. 水资源与水工程学报，2009，20（2）：22—25.]

［17］ Xue W L，Niu W Q，Zhang J，et al. Effects of hydraulic head on soil water movement under moistube-irrigation. Journal of Irrigation and Drainage，2013，32（6）：7—11. [薛万来，牛文全，张俊，等. 压力水头对微润灌土壤水分运动特性影响的试验研究. 灌溉排水学报，2013，32（6）：7—11.]

［18］ Wang R，Sun X H，Guo X H，et al. Numerical simulation for soil water movement at different infiltration heads. Transactions of the Chinese Society for Agricultural Machinery，2011，42（9）：45—49. [王锐，孙西欢，郭向红，等. 不同入渗水头条件下土壤水分运动数值模拟. 农业机械学报，2011，42（9）：45—49.]

［19］ Lu D X，Liu J T，Shang M T，et al. Effects of soil surface ponding depth on infiltration. Agricultural Research in the Arid Areas，2009，27（1）：140—142，156. [陆东旭，刘金涛，尚熳廷，等. 土壤表面积水深度对入渗的影响. 干旱地区农业研究，2009，27（1）：140—142，156.]

［20］ Ye W H. Study on the relationship between solum structure patterns and growth of crops in farm-land of North China plain. Acta Geographica Sinica，1985，40（1）：37—49. [叶文华. 华北平原农田土体构型与作物生长关系的研究. 地理学报，1985，40（1）：37—49.]

［21］ Shao M A，Wang Q J，Huang M B. Soil physics. Beijing：Higher Education Press，2006. [邵明安，王全九，黄明斌. 土壤物理学. 北京：高等教育出版社，2006.]

［22］ Wang C Y，Mao X M，Zhao B. Experiments and simulation on infiltration into layered soil column with sand interlayer under ponding condition. Transactions of the Chinese Society of Agricultural Engineering，2010，26（11）：61—67. [王春颖，毛晓敏，赵兵. 层状夹砂土柱室内积水入渗试验及模拟. 农业工程学报，2010，26（11）：61—67.]

［23］ Huang M B，Zettl J D，Barbour S L，et al. The impact of soil moisture availability on forest growth indices for variably layered coarse-textured soils. Ecohydrology，2013，6（2）：214—227.

［24］ Wang W Y，Wang Q J，Shen B，et al. Infiltration characteristics of soil with double-layer structure in Qinwangchuan area of Gansu Province. Journal of Soil Erosion and Soil and Water Conservation，1998，12（2）：36—40. [王文焰，王全九，沈冰，等. 甘肃秦王川地区双层土壤结构的入渗特性. 土壤侵蚀与水土保持学报，1998，12（2）：36—40.]

［25］ Luo H Y，Yan A F，Xie J H. Experimental investigation of upward movement of soil water in layered systems. Acta Pedologica Sinica，1965，13（3）：312—324. [罗焕炎，严蔼芬，谢驹华. 层状土中毛管水上升的实验研究. 土壤学报，1965，13（3）：312—324.]

［26］ Xie W Y，Fan G S. Influence of moisture content on infiltration characteristics in field soils. Journal of Taiyuan University of Technology，2004，35（3）：272—275. [解文艳，樊贵盛. 土壤含水量对土壤入渗能力的影响. 太原理工大学学报，2004，35（3）：272—275.]

［27］ Zhang J F，Tie X N，Yang X，et al. The impact of initial soil water content on infiltration properties of deep pit infiltration irrigation. Journal of China Agricultural University，2013，18（5）：44—50. [张建丰，帖西宁，杨潇，等. 土壤初始含水率对深层坑渗灌入渗特性的影响. 中国农业大学学报，2013，18（5）：44—50.]

［28］ Zeng C，Wang Q J，Fan J. Effect of initial water content on vertical line-source infiltration characteristics of soil. Transactions of the Chinese Society of Agricultural Engineering，2010，26（1）：24—30. [曾辰，王全九，樊军. 初始含水率对土壤垂直线源入渗特征的影响. 农业工程学报，2010，26（1）：24—30.]

［29］ Zhang X Y，Shi X Z，Yu D S，et al. Effects of antecedent soil moisture on hillslope runoff-generation and soil erosion over red soil-mantled landscapes. Advances in Water Science，2010，21（1）：23—29. [张向炎，史学正，于东升，等. 前期土壤含水量对红壤坡面产流产沙特性的影响. 水科学进展，2010，21（1）：23—29.]

［30］ Malik R S，Butter B S，Anlauf R，et al. Water penetration into soils with different textures and initial moisture contents. Soil Science，1987，144（6）：389—393.

［31］ Wang Q J，Ye H Y，Shi X N，et al. Influence of initial water content on slight saline water infiltration. Journal of Soil and Water Conservation，2004，18（1）：51—53. [王全九，叶海燕，史晓南，等. 土壤初始含水量对微咸水入渗特征影响. 水土保持学报，2004，18（1）：51—53.]

［32］ Liu M X，Nie Y，Yu J. The infiltration process of clay soil under different initial soil water contents. Acta Ecologica Sinica，2012，32（3）：871—878. [刘目兴，聂艳，于婧. 不同初始含水率下粘质土壤的入渗过程. 生态学报，2012，32（3）：871—878.]

［33］ Liu H，Lei T W，Zhao J，et al. Effects of rainfall intensity and antecedent soil water content on soil infiltrability under rainfall conditions using the run off-on-out method. Journal of Hydrology，2011，396（1/2）：24—32.

［34］ Lado M，Ben-Hur M，Shainberg I. Soil wetting and texture effects on aggregate stability，seal formation，and erosion. Soil Science Society of America Journal，2004，68（6）：1992—1999.

［35］ Liu J T，Li X P，Chen X，et al. Distribution characteristics of initial soil water content in profile during hiatus rainfall-infiltration events and its effects on infiltration. Journal of Soil and Water Conservation，2009，23（5）：96—100. [刘金涛，李晓鹏，陈喜，等. 间歇降雨中土壤含水量分布及其对入渗的影响. 水土保持学报，2009，23（5）：96—100.]

Water Infiltration Characteristics of Layered Soil under Influences of Different Factors and Estimation of Hydraulic Parameters

MA Mengmeng, LIN Qing, XU Shaohui†

(College of Environmental Science & Engineering, Qingdao University, Qingdao, Shandong 266071, China)

Layered soil is more often encountered than homogeneous soil in nature, and its water movement follows a law different from the latter’s. And infiltration of water, such as atmospheric precipitation and irrigation water, is an important part of the hydrological process in soil, and is also closely related to groundwater replenishment and pollutant transport. Soil initial water content, soil texture and structure and water supply intensity are all factors affecting the process of water infiltration. The purpose of this study is to explore and grasp law of the water infiltration in layered soil and mechanisms of the influencing factors, and provide a theoretical basis for further rationalization of farmland irrigation measures.The layered soil used in this research, was constructed in line with the soil profile in the field, i.e. a silt loam layer (18cm thick) and a sandy loam layer (24 cm) , and out of the consideration of the mechanisms of ponding water relative to depth, soil configuration and initial soil moisture content affecting water transport. In the indoor ponding infiltration experiment of layered soil, wetting front, cumulative infiltration and soil profile pressure head, relative to depth of standing water, was observed. Moreover, hydraulic parameters of the layered soil were determined with a Ku-pF device and the Hydrus-1D software inversion module, separately. Based on these parameters, the Hydrus-1D model was used to simulate and predict water transport under various set conditions. Applicabilities of the soil hydraulic parameters were verified by comparing the simulated data of the two sets of parameters.Results show that the wetting front turned from nonlinear advance to linear advance and the cumulative infiltration increased with time, while the infiltration rate decreased rapidly in the early stage of the infiltration and then slowly as the infiltration going on, which is mainly due to the change in soil matrix potential gradient. The soil was relatively dry and high in water suction at the initial stage of the infiltration; as the soil increased in water content, the water suction decreased. As affected by the three factors, water transport varied sharply in characteristics in the layered soil. When the ponding water increased in depth and the initial soil water increased in content, both the wetting front advancing rate and the infiltration rate increased, and the pressure water head increased quicklyat each observation point and the soil water unsaturation degree decreased, which indicates that the change in depth of ponding depth has some impact on pressure potential, and the change in initial water content is related to matrix potential and disintegration and compression of soil aggregates. Compared with the soil configuration of silt loam overlying sandy loam, the one of the reverse order was higher in overall wetting front advancing rate, infiltration rate and pressure head variation. (The infiltration rate at the interface of the wetting front in the layered soil was 0.20 and 0.021 cm·min–1, respectively.) In addition, the two types of layered soils differed significantly in variation of the pressure water head in the soil water redistribution processAll the findings in this study not only help illustrate that appropriate adjustment of the three influencing factors can reduce soil leakage and optimize soil water management in the field, but also further demonstrate that the parameters of the inversions are more adoptable to simulation and prediction of water infiltration characteristics of layered soils under ponding water in indoor experiments.

Layered soil; Soil configuration; Ponding depth; Initial water content; Hydrus-1D

S152

A

10.11766/trxb201905090250

马蒙蒙，林青，徐绍辉. 不同因素影响下层状土壤水分入渗特征及水力学参数估计[J]. 土壤学报，2020，57（2）：347–358.

MA Mengmeng，LIN Qing，XU Shaohui. Water Infiltration Characteristics of Layered Soil under Influences of Different Factors and Estimation of Hydraulic Parameters[J]. Acta Pedologica Sinica，2020，57（2）：347–358.

* 国家自然科学基金项目（41571214，41807010）资助Supported by the National Natural Science Foundation of China（Nos. 41571214，41807010）

，E-mail：shhxu@qdu.edu.cn

马蒙蒙（1995—），女，山东德州人，硕士研究生，主要从事土壤水和溶质运移的数值模拟。E-mail:mengmengma127@163.com

2019–05–09；

2019–07–10；

优先数字出版日期（www.cnki.net）:2019–10–29

（责任编辑：檀满枝）