库区边坡地震-渗流耦合数值模拟
2020-04-24蒋晓君周柯军葛万明
蒋晓君,周柯军,葛万明,杨 帆
(1.无锡市太湖闸站工程管理处,江苏 无锡 214023,2.无锡市惠山区阳山镇水利农机服务站,江苏 无锡 214023,3.无锡市水利设计研究院有限公司,江苏 无锡 214023,4.无锡市泓利工程监理有限公司,江苏 无锡 214023 )
地震是危害边坡稳定的关键性因素[1-3],地震-库水位共同作用下,坝体与坝基会产生超孔隙水压力[4-5],使得坝体与坝基的有效应力急剧减小,导致地面喷砂冒水、沉降不均匀、地基失效、滑坡等一系列灾害[6-9],因此,对库区边坡动力-渗流耦合下的边坡力学相应的认知是正确把握地震灾害机理及防治地震边坡失稳的关键。
国内外学者对地震-渗流耦合下的边坡稳定展开了一定的研究工作,主要集中于理论、试验及数值模拟上,理论方面:杨长卫[10]等利用Hilbert-Huang变换,提出SV波作用下岩质边坡地震稳定性的时频分析方法;肖世国[11]等基于限分析上限定理,推导了黏土土坡永久位移的计算方法;高科[12]基于突变级数理论,对边坡的地震稳定性进行了综合评定。试验方面:叶海林[13]采用大型振动台,对边坡动力破坏特征进行了室内试验研究;张泽林[14]对黄土-泥岩边坡动力相应进行了离心机试验。数值模拟方面:范昊天[15]利用离散元软件PFC对含软弱夹层边坡地震作用下的破坏规律进行了数值模拟;李源亮[16]建立了边坡的节理有限元模型,对其不同参数进行了敏感性分析。但是以上研究多针对边坡失稳最终形态或者边坡某点的应力状态进行分析,较少对地震-渗流耦合下的孔压,位移及安全稳定评价进行全面分析。
本文基于某堤坝工程,利用岩土软件Geostudio中的SEEP/W,SLOPE/W及QUAKE/W模块,实现了堤坝渗流-地震耦合计算,重点研究了地震作用下的浸润线,超孔压,特征点位移,永久位移及动力稳定性,研究成果为全面认识堤坝渗流-地震动力稳定性规律提供了一定的参考。
1 计算理论
1.1 非饱和渗流原理
非饱和渗流微分方程可以表达成为公式(1):
(1)

1.2 地震动力分析方法
动力作用下土体趋向软化,因此,可以利用G/Gmax来刻画等效线性模型中的现象如公式(2)~(4):
(2)
K(γ,PI)=
(3)
(4)
其中,G为地震作用下的土体瞬时剪切模量,Gmax为0应变时的剪切模量,γ为土体容重,PI为塑性指数,n(PI)为和塑性指数有关的函数。
地震中的动水压力是周期N的函数,NL是特定土体在特定地震条件下造成液化所需施加的应力周期数,孔隙水压力比γu与N/NL有关,如公式(5)所示:
(5)
其中,孔压可以表达成为公式(6):
μ=γu×δ(static)
(6)
式中:μ为动孔隙水压力,γu是孔隙水压力比,δ(static)是有效静态围压。
1.3 地震-渗流耦合下的动力稳定计算理论
根据抗滑稳定的定义,边坡的动力安全系数可以表达成为公式(7):
K=
(7)
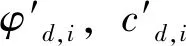
2 计算模型及边界条件
2.1 计算模型
计算模型选择某水库堤坝,坝高44 m,坝基厚度取为10 m,坝基宽度为350 m,坝顶宽为16 m。该堤坝坝壳料为黏质砂,坝内为中密砂,而坝基材料则为花岗岩。该堤坝的正常蓄水位为33 m,下游设置排水。一共设置18个监测点来监测坝体内部的孔隙水压力、位移变化规律,分别标号为1#~18#,相应位置见图1红点标注。整个模型一共划分为1612个节点,1689个单元。
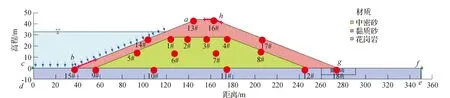
图1 计算模型及模型网格
2.2 边界条件
对模型进行渗流应力分析需要知道渗流及应力初始条件,渗流初始条件为边界abcd33 m水头计算所得的稳定渗流场作为整个模型渗流计算的初始条件,应力初始条件则是cd、fe固定x向位移,de固定xy向位移下的地应力平衡结果作为整个工况下的初始应力场。
边界条件设置如下,渗流边界为:abc为33 m定水头边界,gf为排水边界,其余边界为不透水边界。进行地震动力计算边界为:de为固定xy向位移边界,cd,fe则为固定y向边界。
3 计算参数设置
不同材料的非饱和渗流参数根据VG模型进行估算,材料物理力学参数如表1所示,渗透系数函数及体积含水率函数如图2所示。土体的动力参数采用非线性模型,动力特性如图3所示。地震波的时程曲线见图4。

表1 材料物理力学参数

图2 土-水特征曲线函数
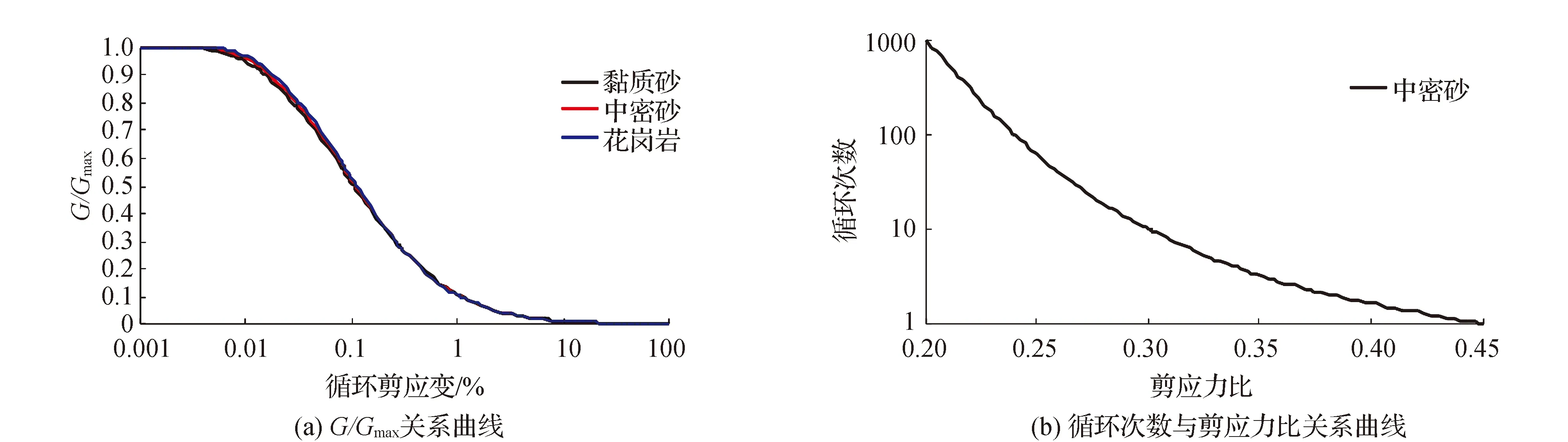
图3 土体动力特性曲线
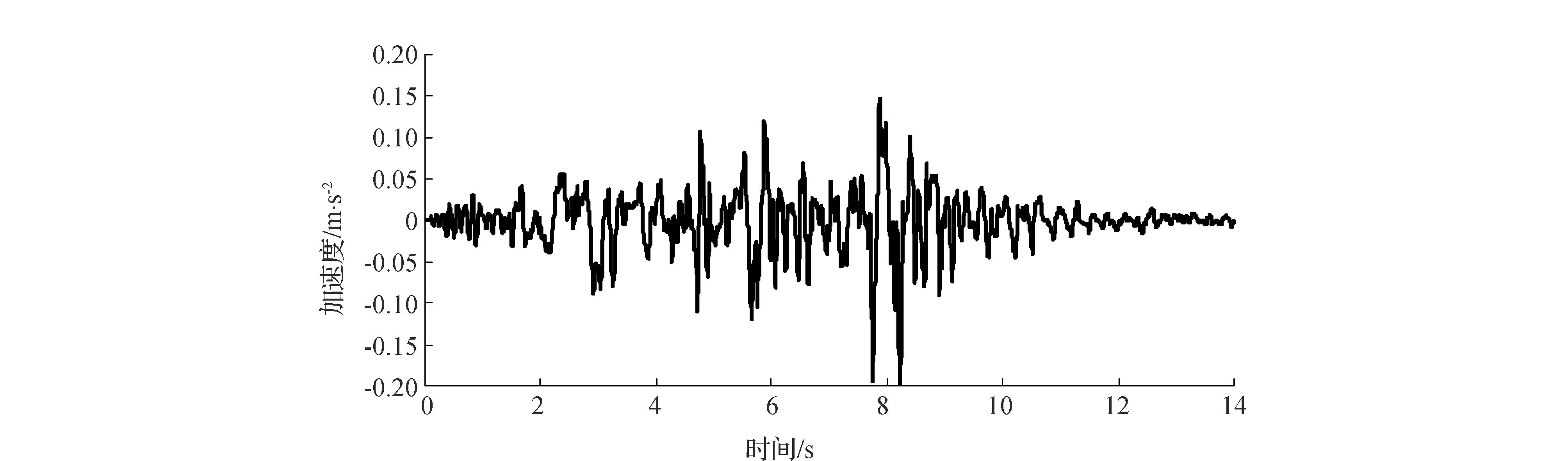
图4 地震加速度时程曲线
4 结果分析
4.1 动孔压分析
图5为监测点1#~12#的超孔隙水压力随时间的变化规律。其中监测点1#~4#代表中密砂的上部,监测点5#~8#代表中密砂的中部,而监测点9#~12#代表中密砂的下部。
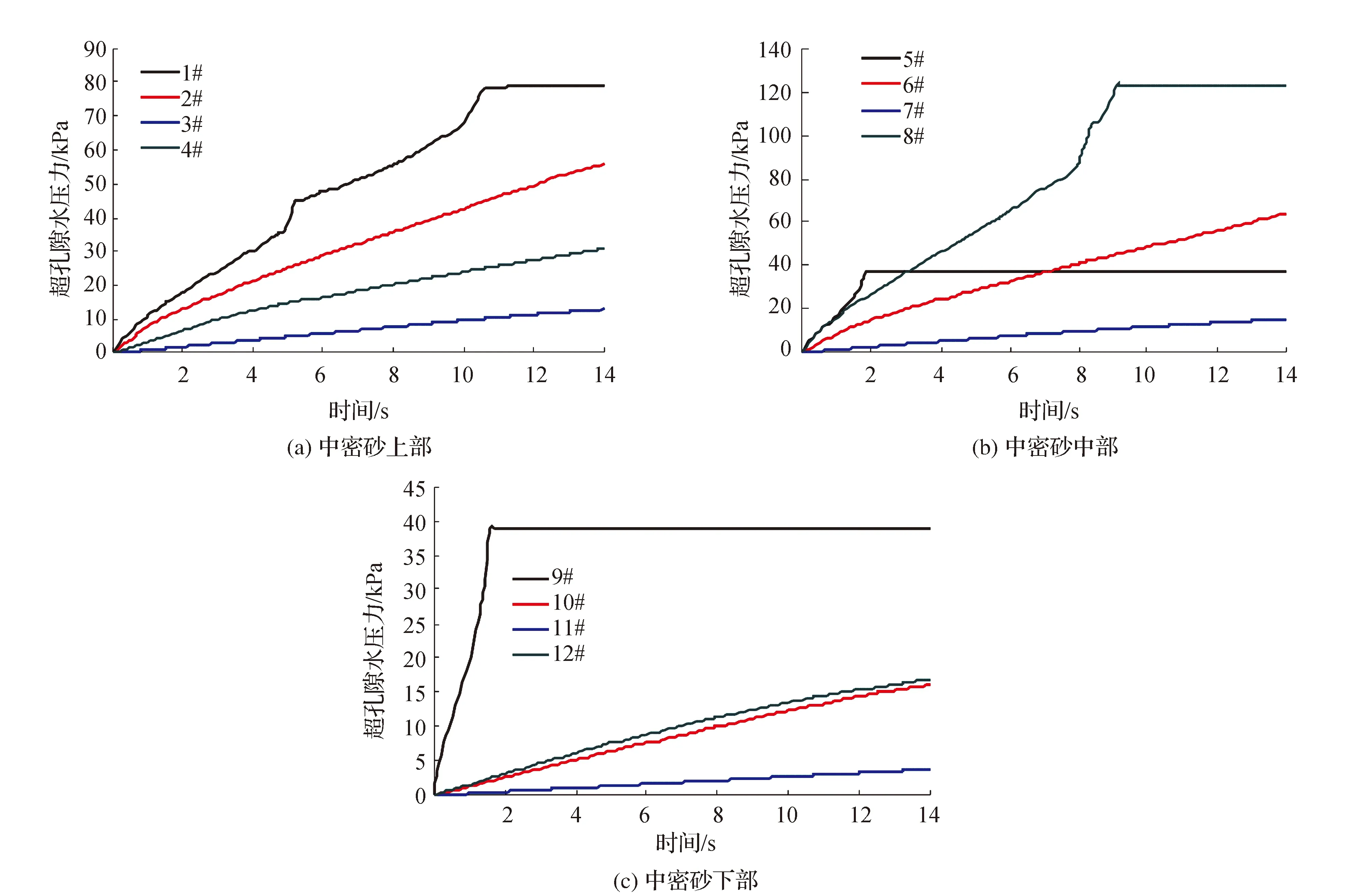
图5 中密砂不同监测点的超孔压变化规律
由图可见:随着地震的持续,堤坝内部超孔压呈现不断上升的趋势。对于中密砂上部监测点,不同监测点(1#、2#、3#、4#)的超孔压的增量分别为80.1 kPa,55.6 kPa,10.2 kPa及29.8 kPa,可见对于上部监测点而言,监测点越靠近上游,超孔隙水压力的数值越大。
对于中密砂中部监测点而言,当监测点位于上游侧(监测点5#、6#及7#),超孔压增幅不大,分别为38.2 kPa,19.2 kPa及61.1 kPa,而位于下游侧的监测点8#孔压增幅最大为128.1 kPa,且位于下游侧的监测点在地震未结束时超孔压便已经达到最大并在随后的地震过程中保持不变。
对于中密砂下部监测点,超孔压的增幅明显低于上部与中部。位于上游侧的监测点9#超孔压增幅最大,为38.8 kPa,而其他监测点(10#、11#、12#)的超孔压增幅最小,分别为16.1 kPa、3.7 kPa和17.0 kPa。
4.2 位移量分析
选取如图1所示的13#~16#测点进行位移监测,堤坝在地震作用下的位移变化规律如图6所示。
由图可见:对于上下游测点而言,监测点高程越高,水平向的位移变化幅度越大,位于坝体上部的监测点13#和14#的水平向位移在地震过程中的变化比底部监测点大,在3.3 s达到最大值,约为12 cm。坝顶处的水平位移最大,上游坝脚处的水平位移最小。但是上下游测点的水平位移变幅差别不大。
堤坝上游侧竖向位移变幅要大于下游侧,但是竖向位移的变幅要远小于水平位移变幅。顶监测点13#的最大竖向位移为0.06 m,出现在8.6 s;14#为0.0304 m,出现在9.1 s;15#为0.0056 m,出现在8.3 s。输入加速度的最大值出现在8.22 s,可知坝体最大竖向位移滞后于输入加速度最大值。竖向位移随时间的变化曲线与输入加速度较为接近,但是有滞后效应。下游侧土体竖向位移变化规律与上游侧相似,竖向位移最大值都是坝顶>坝中>坝脚,但是最大值小于上游侧;坝顶、坝中和坝脚最大值分别为0.037 m、0.035 m和0.015 m。
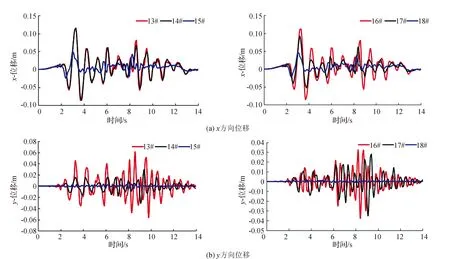
图6 堤坝上下游不同测点的位移变化规律
4.3 安全系数变化规律
地震作用下的上下游坝坡的安全系数变化规律如图7所示。
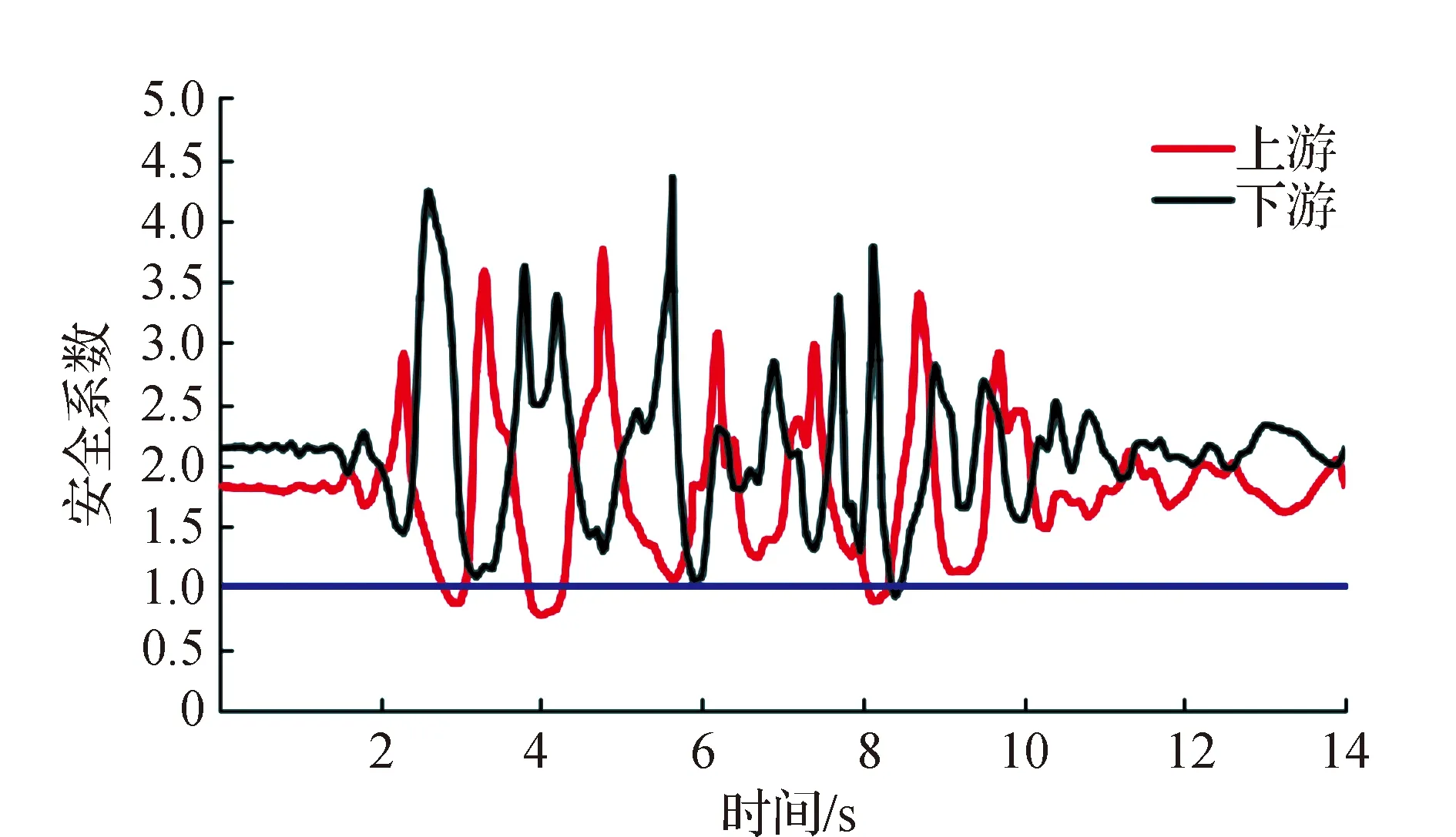
图7 堤坝动力安全稳定及永久位移
由图可见:上下游坝坡在地震过程中均出现小于1的情况,但是上游坝坡最小安全系数为0.82,要小于下游坝坡的0.91,表明在地震过程中上游坝坡更容易失稳,结合动压力与后移量分析可知,地震过程中的上游侧的超孔压较高,有效应力较低,容易发生液化失稳,因此上游侧的安全系数较低。
5 结 论
(1)地震作用下堤坝内部浸润线具有一定变化,主要升高部位在于中密砂内部,而在黏质砂部位浸润线的变化幅度则不大。
(2)堤坝内部中密砂上部及中部的有效应力变化剧烈,下部变化幅度较小,且临近上游侧的上部地震过程中发生液化失稳。
(3)上下游坝坡在地震过程中均出现小于1的情况,上游坝坡最小安全系数为0.82,下游坝坡最小安全系数为0.91,表明地震过程中上游坝坡更容易失稳。
